基于刚柔耦合模型的动车组齿轮箱箱体振动特性研究
2020-07-21高国川张建超郭文武
高国川,2, 张建超, 郭文武
(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043;2.石家庄铁道大学 机械工程学院,河北 石家庄 050043)
0 引言
我国铁路事业发展迅速,高速动车组已成为旅客出行的重要交通工具。齿轮箱箱体在列车运行中起到传递动力和连接的作用,长期在重载和高速的工况下服役,属于车辆振动较为激烈的簧下部分[1-2]。据统计,有些箱体已经出现裂纹或破裂等不同形式和程度的故障,因此对箱体的振动特性进行分析,能够为其结构优化提供参考,从而保障动车组的安全稳定运行。
当前,国内外一些学者已经开始对机车齿轮箱的动力学特性进行研究。李翠省和王贞云等[3-4]建立了机车齿轮传动系统的动力学模型,分析了不同程度的断齿故障对箱体振动信号的影响,研究过程中未对箱体进行柔性化处理;李广全[5]分析了不同外载荷下箱体的应力响应,发现运行速度、方向及线路条件对箱体的应力响应均有不同程度的影响,研究过程中未考虑轴承对箱体振动的影响;孙刚等[6]建立了动车组整车的刚柔耦合动力学模型,发现轨道激扰和车辆运行速度对传动系统振动影响十分明显,研究过程中未指出箱体振动响应较为明显的区域;Hiroaki[7]建立了齿轮箱的有限元模型,发现齿根点蚀时箱体振动响应较为明显,对后续学者的研究有借鉴之处;黄冠华[8]建立了高速列车整车动力学模型,提出了髙速列车齿轮传动系统振动参考值和齿轮箱设计时的振动参考值,建模过程中未考虑轴承对齿轮传动系统的影响;Michalek et al[9]建立了机车轮轴驱动系统的动力学模型,分析了牵引电机的不同悬挂方式对齿轮箱振动特性的影响;王海龙等[10]采用建模方法分析了高速列车齿轮箱齿轮的接触应力,发现接触应力在齿轮启动阶段较大并且会出现波动,影响箱体的安全性,研究过程中未分析箱体的振动响应;韩博跃等[11]提出将小波阈值和约束独立分量相结合的算法,用于识别断齿时箱体的振动信号特征,结果表明该种方法能有效提取出故障信号特征;林新海等[12]通过模态试验和台架试验相结合的方法,分析了动车组齿轮箱的振动特性,发现在特定转速下箱体会发生共振,研究过程中未分析箱体在高频激励下的振动响应。
综上可知,目前对动车组齿轮箱箱体振动特性的相关研究相对较少,并且对箱体进行研究时也多数将其当作刚性体处理。事实表明,用柔性箱体模拟列车的高速运行,能直观地反映出箱体受到激励后的振动响应情况[13]。综合运用SolidWorks三维建模软件、ANSYS有限元分析软件和ADAMS动力学仿真软件建立箱体柔性、齿轮系统刚性的刚柔耦合模型,分析箱体在齿轮啮合激励下的振动特性,为箱体结构的进一步优化提供相关依据。
1 齿轮箱整体模型的建立
以国内某型动车组齿轮箱为研究对象,其中箱体由上、下两部分组成,如图1所示。上、下箱体均在表面设置了多处加强筋以减少振动和提高强度,从而达到降低车内噪音和提高乘坐舒适度的目的,二者装配时采用紧固螺栓进行联结。

图1 齿轮箱上、下箱体
图2 完整齿轮箱装配体
利用SolidWorks软件建立该上、下箱体三维模型时,在保留箱体实际结构形式的基础上,需要简化一些对结构分析影响甚小的特征,例如螺纹孔、圆角、倒角和小凸台等;在装配时可以忽略上、下箱体之间的螺栓连接,将上下箱体视作一个整体;并且需要将其模型原点与装配体默认坐标系原点重合,以将齿轮箱整体模型导入到ADAMS后,保证模型坐标原点与ADAMS默认坐标原点重合,便于仿真之前各个参数的设置和准确地进行动力学仿真。
根据动车组齿轮箱内大小齿轮的相关参数(见表1),通过迈迪工具集参数化创建大小齿轮的三维模型,在模型基础上建立齿轮轴模拟轴和齿轮之间的过盈配合;根据轴承型号,调用Toolbox工具箱中轴承件来完成箱体整体结构的装配,为了清楚地显示各个结构,故在模型中简化了轴承端盖,整体结构装配体如图 2所示。

表1 大小齿轮参数
2 刚柔耦合模型的建立
为了模拟出箱体在列车运行中受到高频激励时产生的动态响应,通过ANSYS软件将箱体进行柔性化处理,在ADAMS软件中建立箱体柔性、齿轮系统刚性的刚柔耦合模型。
根据表2中的数据在ANSYS软件中设置箱体的材料属性,使用SOLID 187实体单元对箱体进行网格划分。划分过程中采用Smartsize智能控制网格在倒角、圆角以及曲面处的大小与稀疏程度,提高划分的网格质量,使箱体的振动响应更加接近实际情况。

表2 箱体材料力学性能
在箱体轴承座所在圆柱面的中心创建4个关键点,并用MASS 21单元分别对关键点进行网格划分,建立用于在柔性体导入ADAMS软件后生成与其他刚性体联结的节点。分别以上述4个关键点为主节点、轴承座所在圆柱面上所有节点为从节点,建立刚柔耦合模型中刚性体和柔性体连接处的刚性区域,如图3所示。
柔性箱体的载体是包含构件模态信息的中性文件,输出中性文件时需要去掉箱体前6阶自由模态后,再输出前20阶模态用于分析箱体在高频激励下的振动响应。将齿轮箱装配体模型导入到ADAMS软件中,通过Flexible Bodies功能将生成的柔性箱体导入到该模型中替换掉原来的刚性箱体,再设置好柔性箱体与其他刚性体之间的约束,即可生成齿轮箱的刚柔耦合模型,如图4所示。
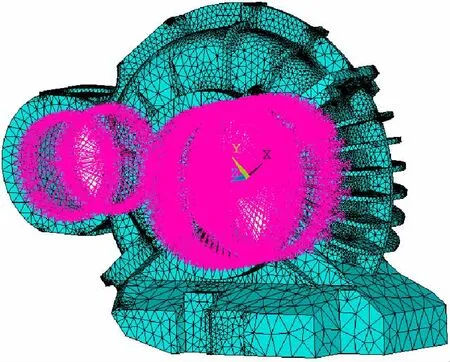
图3 箱体刚性区域

图4 齿轮箱刚柔耦合模型
3 参数的设置
本文主要研究齿轮啮合产生的内部激励下箱体的振动特性。小齿轮通过联轴器与电机相连,电机转速很快,小齿轮轴承座处振动响应可能较明显;上箱体观察口位于齿轮啮合处,由于啮合力的冲击,振动响应可能较为明显;实际情况中箱体类似处于悬空状态,顶端振动响应可能较为明显。结合以上分析,在柔性箱体上设置5个不同测点,用以监测所在区域的振动响应。各个测点具体位置,如图4中标记所示。测点1位于上箱体小齿轮轴承座处;测点2位于上箱体观察口处;测点3位于上箱体顶端处;测点4位于上箱体大轴承座处;测点5位于下箱体大轴承座处。
为了避免仿真过程中驱动和负载出现陡变,需要在小齿轮轴上添加“step函数”控制的旋转驱动,并在大齿轮轴上添加“step函数”控制的负载转矩。step函数形式为:step=(x,x0,h0,x1,h1),其中
(1)
式中,b=h1-h0;Δ=(x-x0)/(x1-x0) ,x为自变量,x0为step函数自变量的初始值,x1为step函数自变量的结束值;h0为step函数的初始值;h1为step函数的结束值。step函数意义为:在自变量x由x0到x1的时间内,函数值由h0平缓变化为h1。
仿真时模拟动车组在250 km/h的速度下运行,小齿轮转速为3 500 r/min,负载转矩大小设置为3 800 N·m。经换算,最终确定的旋转驱动函数为
step=(time,0,0,0.1,-21 000d)
(2)
负载转矩函数为
step=(time,0,0,0.1,-3 800 000d)
(3)
由于齿轮转速较快,相同仿真时间内步长设置得越小,输出的仿真结果次数越多(表示采样频率越大),测得的数据越接近箱体实际振动情况,故仿真时间设为0.5 s,仿真步长设为0.000 1 s。
4 仿真结果的分析
对齿轮箱系统进行驱动仿真后,发现5个测点在x、y、z方向均出现一定的振动位移、速度和加速度响应,其中0~0.1 s启动过程中振动较为强烈,0.1 s后振动趋于稳定,并维持在某一区域范围波动。相关文献表明[14-15],箱体振动的位移极值、速度极值和加速度极值出现的位置没有必然联系,由此对各个测点的振动位移、速度和加速度响应进行分析,以期分别得到箱体振动位移、速度和加速度响应较为明显区域,为箱体的结构优化和检测监测提供参考。
4.1 测点振动位移
对上述5个测点的三向振动位移变化量进行统计分析,启动过程中最大振动位移和稳定后平均振动位移结果见表3。
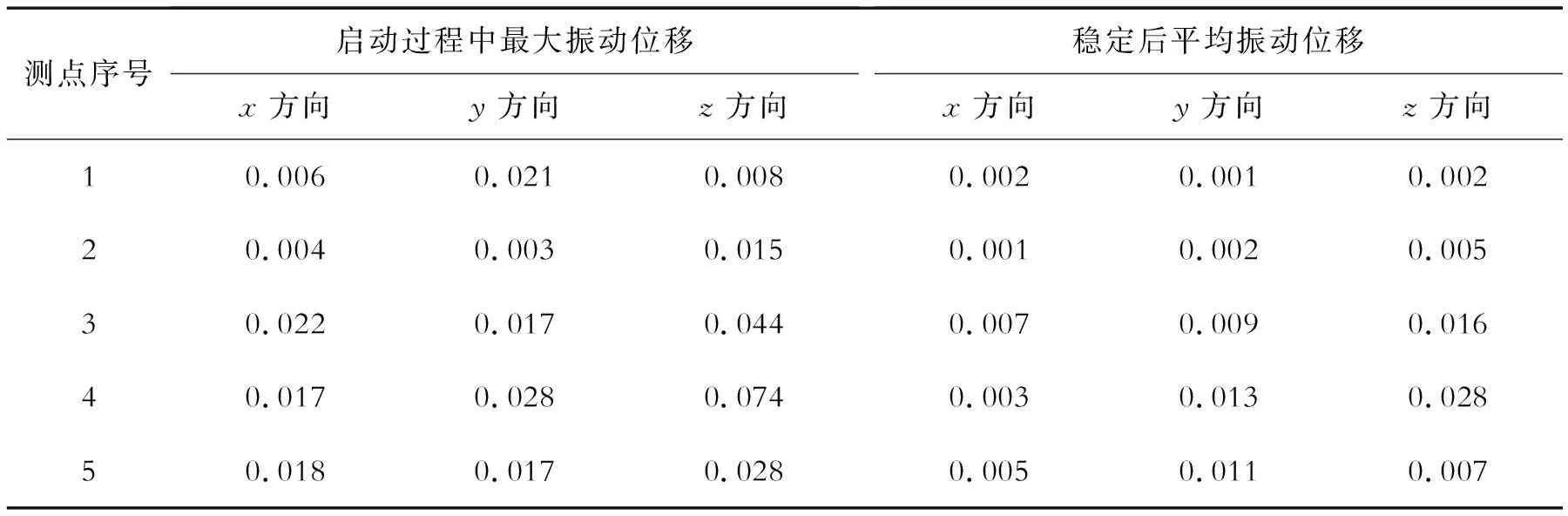
表3 5个测点振动位移 mm
由表3得知,箱体上每个测点在启动过程中产生的振动位移变化均较大,自0.1 s稳定后,箱体振动位移量趋于很小,但同一时刻同一方向的5个测点振动位移量均不相同。启动过程中和稳定后,测点3(上箱体顶端处)和测点4(上箱体大轴承座处)的振动位移量与其他测点相比均较为明显,其三向振动位移时域图分别如图5、图6所示。所研究箱体受到的齿轮啮合激励为高频激励,由于位移幅值对高频激励不敏感,频域图中的幅值变化不明显,故未列出上述测点的位移频域图。
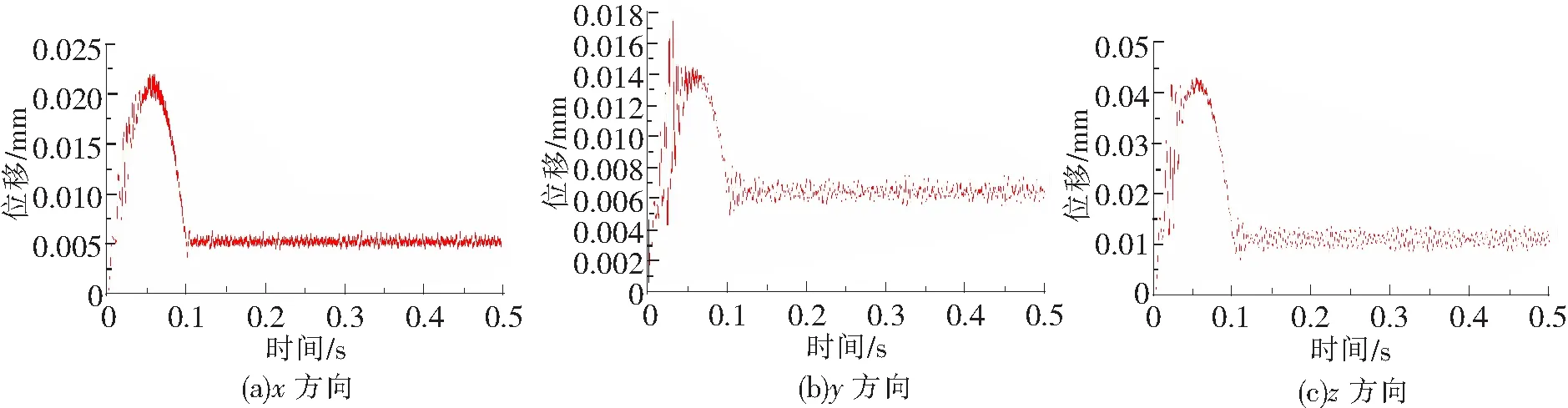
图5 测点3位移时域图

图6 测点4位移时域图
分析原因主要是:上箱体同时承受大齿轮轴和小齿轮轴传递的振动冲击,上箱体顶端距箱体固定位置较远;大齿轮转速较快,轴承座处受到的振动冲击也较大,故在启动过程中和稳定后,箱体振动位移变化较为明显区域出现在上箱体顶端和大轴承座处。虽然振动位移量较小,但在长期的运行中,即便是小的位移量也会导致箱体疲劳,进而引起箱体故障。
4.2 测点振动速度
对上述5个测点的三向振动速度变化量进行统计分析,启动过程中最大振动速度和稳定后平均振动速度结果见表4。
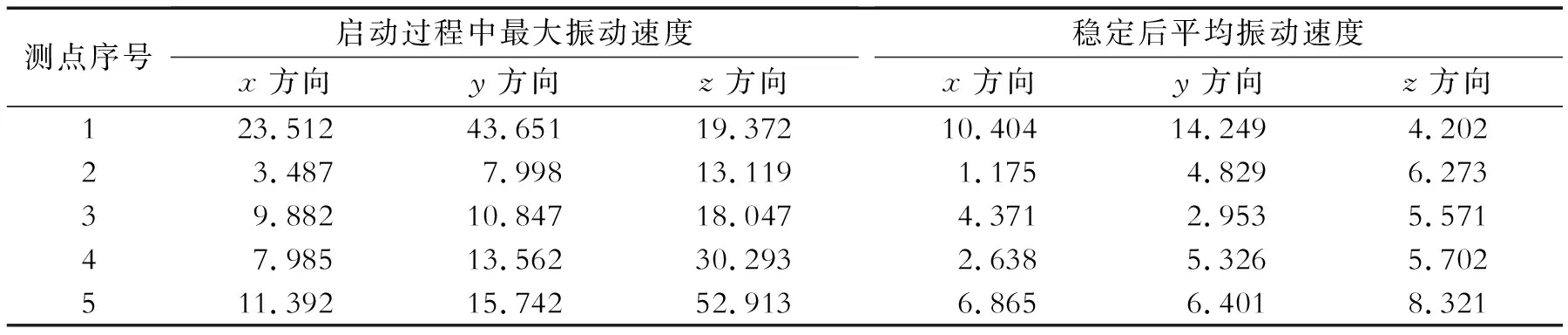
表4 5个测点三向振动速度 mm/s
由表4得知,箱体上每个测点在启动过程中产生的振动速度变化均较大,自0.1 s稳定后,箱体振动速度趋于很小,但同一时刻同一方向的5个测点振动速度均不相同。
启动阶段和稳定后,测点1(小齿轮轴承座处)和测点5(下箱体大轴承座处)的振动速度量与其他测点相比均较为明显,其三向振动速度时域图分别如图7、图8所示。测点1和测点5的速度频域图中均在2 040.52 Hz处幅值最大,故只列出测点1的速度频域图,如图9所示。
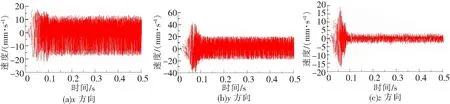
图7 测点1速度时域图
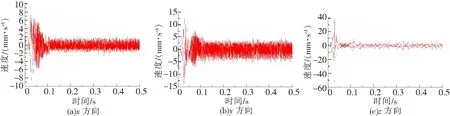
图8 测点5速度时域图
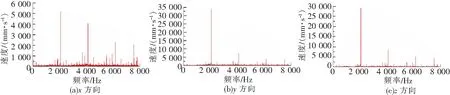
图9 测点1速度频域图
分析原因主要是:小齿轮轴承座距离电机较近,启动过程中电机转速较快,小齿轮转速与电机转速相同,对其轴承座的冲击较大;下箱体虽与上箱体通过螺栓固定但类似处于悬空状态,且受到大齿轮轴的作用力和转速冲击也较大,同时还要承受大齿轮及大齿轮轴的重力,故在启动过程中和稳定后,箱体振动速度较为明显区域出现在小齿轮轴承座和下箱体大轴承座处。
4.3 测点振动加速度
对上述5个测点的三向振动加速度变化量进行统计分析,启动过程中最大振动加速度和稳定后平均振动加速度结果见表5。
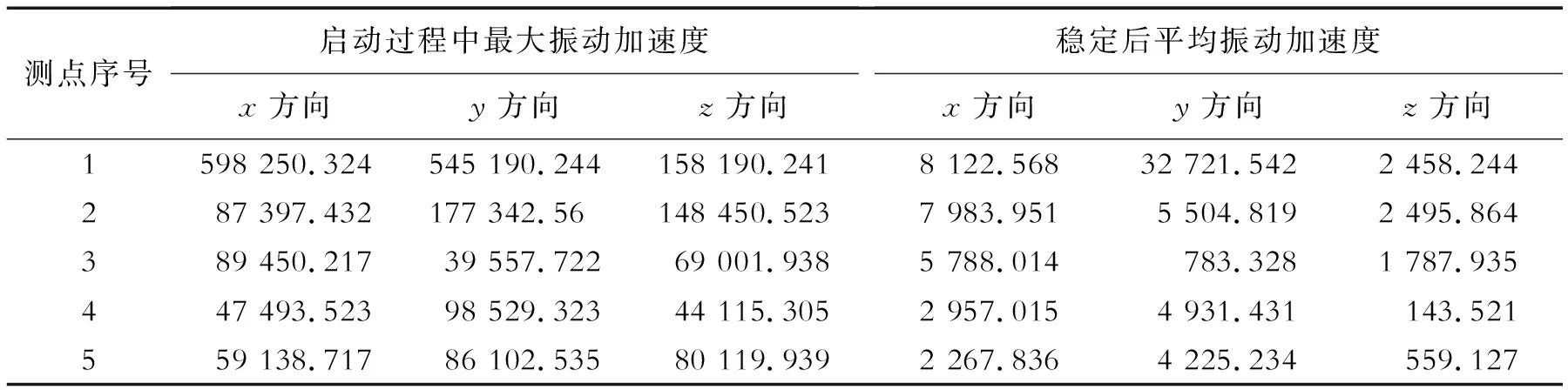
表5 各个测点振动加速度 mm/s2
由表5得知,箱体上每个测点在启动过程中产生的振动加速度变化均较大,自0.1 s稳定后,箱体振动加速度有一定的减小,同一时刻同一方向的5个测点振动加速度也均不相同。
启动阶段和稳定后,测点1(小齿轮轴承座处)和测点2(上箱体观察口处)的振动加速度量与其他测点相比均较为明显,其三向振动加速度时域图分别如图10、图11所示。测点1和测点2的速度频域图中均在2 040.52 Hz处幅值最大,故只列出测点2的加速度频域图,如图12所示。
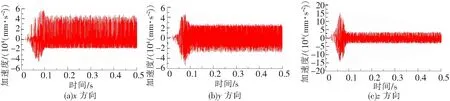
图10 测点1加速度时域图
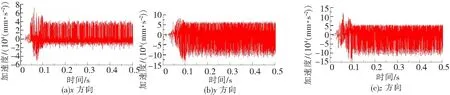
图11 测点2加速度时域图
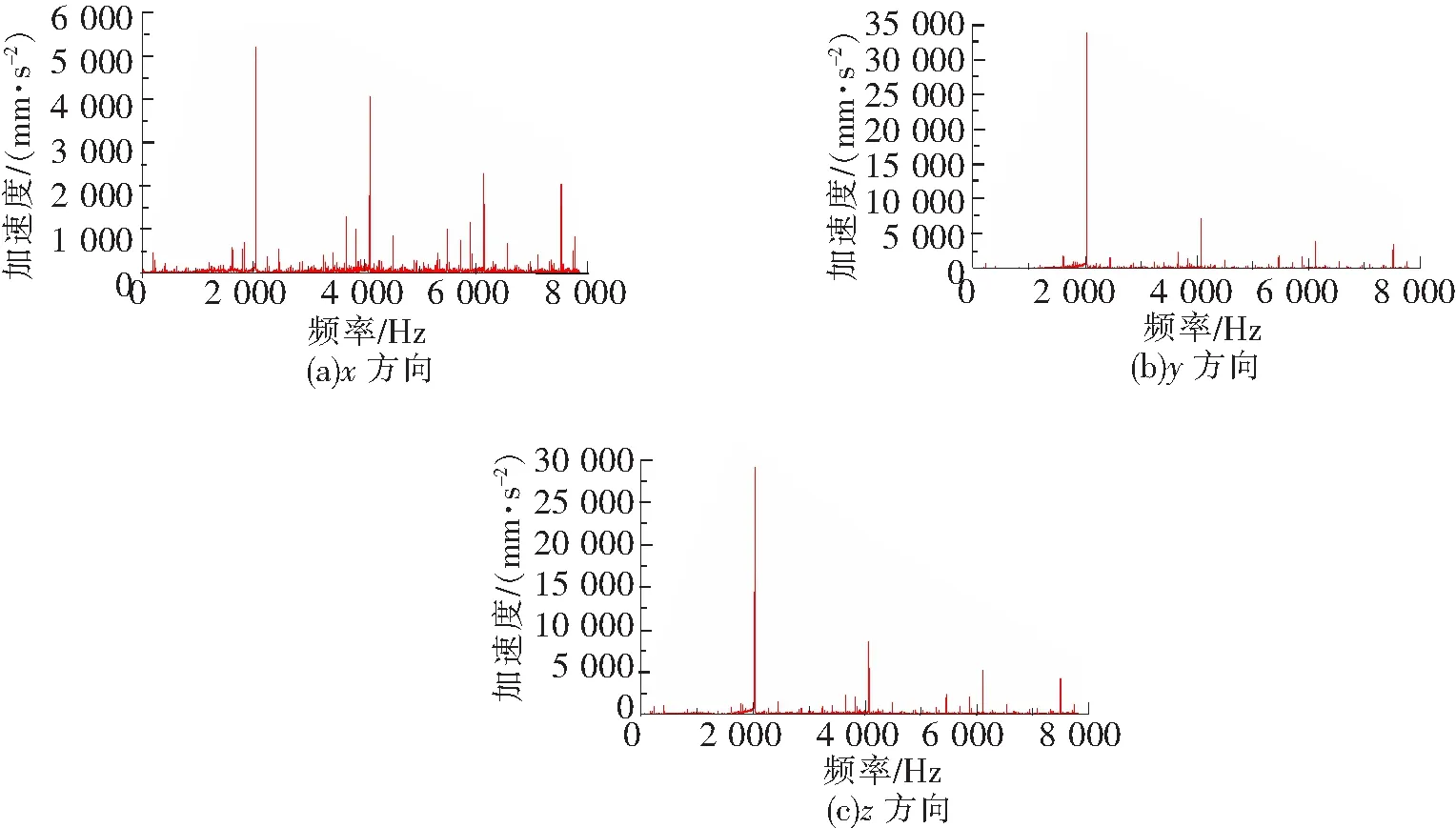
图12 测点2加速度频域图
分析原因主要是:小齿轮轴通过联轴器与牵引电机相连,电机转速较快,联轴器和小齿轮轴均会对轴承座产生一定的振动冲击,且冲击较大;上箱体观察口处位于齿轮啮合冲击交汇部位,受到大小齿轮传递的振动冲击较大,且该处为弯曲结构,承受冲击能力较差,故在启动和平稳阶段,箱体振动加速度较大的地方出现在小齿轮轴承座和上箱体观察口所在区域。
由图9和图12知,箱体不同测点的速度和加速度响应均在2 040.52 Hz处幅值最大,表示仿真所得啮合频率为2 040.52 Hz,与理论啮合频率2 041.66 Hz相差无几,表明箱体各个测点的响应频率相同,均为齿轮的啮合频率。频域图中在啮合频率处响应幅值最大,在2倍频和3倍频处幅值出现了衰减,与实际情况接近,表明模型建立的较为准确,能够较好地体现出箱体的振动特性。
5 结论
以国内某型动车组齿轮箱为研究对象,运用SolidWorks、ANSYS和ADAMS软件建立了齿轮箱系统的刚柔耦合模型,并着重对齿轮啮合激励下箱体的动力学特性进行了仿真分析。基于将箱体柔性化的方法,能够获得箱体上各点3个方向振动的位移、速度和加速度变化情况,并且发现同一测点在启动和平稳不同阶段的振动响应变化很大,在同一时刻箱体上5个测点的振动参数也均不相同,上箱体顶端和上箱体大齿轮轴承座处的振动位移较为显著,小齿轮轴承座和下箱体大齿轮轴承座处的振动速度较为明显,小齿轮轴承座和上箱体观察口处的振动加速度较为突出。箱体各个测点的响应频率相同,为齿轮的啮合频率。
以上基于刚柔耦合的仿真研究及其结论,可以为齿轮箱体的结构优化提供参考依据,进而保障动车组的安全稳定运行。
