激光康普顿散射产生带轨道角动量的X射线方案研究
2020-07-20耿和平武海龙陈建辉赵振堂
耿和平 武海龙 陈建辉 赵振堂
1(中国科学院上海应用物理研究所 上海 201800)
2(中国科学院大学 北京 100049)
3(中国科学院上海高等研究院 上海 201210)
随着激光技术的出现与蓬勃发展,人们慢慢认识到了光的力学效应的巨大应用前景,而带轨道角动量(OrbitalAngular Momentum,OAM)的涡旋光束凭借其特殊的光学性质和可观的应用前景吸引了越来越多人的关注。涡旋光束是一类在传播方向上相位随方位角变化的光束,其典型的特征是光强在横截面内呈环形分布,波前具有螺旋形结构[1-2]。螺旋形波前可以聚焦成环形的光陷,形成光学涡旋[3],使得涡旋光束在光学操控领域具有可观的应用前景,逐渐成为近几年光学学术界的热门研究课题[4-6]。光学涡旋在可见光波段的基础和应用研究已经取得了很多成果[7]。在过去20年的研究过程中,也已形成了一系列成熟可控的涡旋光束的产生方法,这些方法包括:螺旋相位板[8]、空间光调制器(spatial light modulator)[9]、Q-盘 片[10]、椭 圆 模 式 转 换器[11]等。
有鉴于涡旋光束和光学涡旋的卓越特性和可观的应用前景,如何将其使用范围扩展到X射线波段已逐渐成为近几年激光学术界以及X射线学术界交叉的热门研究课题[12]。澳大利亚Peele等[13]在美国第三代同步辐射光源装置APS(美国阿贡国家实验室,The Advanced Photon Source)上利用螺旋相位板技术产生了光子能量为9 keV的X射线波段的涡旋光束;意大利科学家Cojoc等[14]在意大利第三代同步辐射光源Elettra上采用衍射光学元件(Diffractive optical Elements,DoE)技术产生了高电荷态(m=64)的光子能量为700 eV的X射线涡旋光束;瑞士科学家 Bernd Terhalle 等[15]采用 计 算机编 程全息 术(computer generated holograms)产生了波长为13.5 nm的极紫外涡旋光束,并应用于光刻。德国Jena大学科学家们[16-17]采用传统激光的高次谐波辐射技术产生极紫外光(Extreme-ultraviolet,XUV)涡旋光束,同时还保持了激光的品质;加拿大科学家Paul Corkum教授研究组[18]也展开了相关的研究。美国阿贡国家实验室的Ian McNulty博士系统研究了利用螺旋型波荡器产生带轨道角动量X射线的方法[19-20]及其在磁性材料科学中的应用前景[21]。由此可能扩展的应用领域包括:光刻、X射线宇宙学、X射线显微、微型机械等[12]。带轨道角动量X射线与物质相互作用也呈现一些前所未知的新特性[22-23],这将为X射线物理与X射线光学开拓全新的探索领域[24]。
2014年,Seipt及其同事[25]利用激光逆康普顿散射产生高能量的扭曲转动电子,这些电子在运动过程中发射出具有螺旋结构的X射线束。随后,2016年,Petrillo及其同事[26]研究了使用一个相对论性的高亮度电子与一个OAM的激光脉冲发生汤姆孙(逆康普顿)背散射的方法产生带OAM的X-γ射线脉冲;2017年,Taira等[27]从理论证明了高功率圆极化激光与相对论电子的非线性激光康普顿散射(Laser Compton Scattering,LCS)产生的高次谐波为涡旋光束,该结果解释了2015年于布鲁克海文国家实验室的加速器试验装置(Brookhaven National Laboratory Accelerator Test Facility,BNL ATF)[28]上进行的非线性LCS实验结果。实验中采用65 MeV的电子束与高功率圆极化激光进行碰撞,观察到其二次谐波的光强分布呈环形结构,具有典型的涡旋光束的结构。
激光康普顿散射源是利用高功率激光与相对论电子束碰撞,将电子的一部分能量转移给光子,从而得到X/γ射线的一种辐射源。目前国际上已经有多个科研院所进行了LCS相关的理论和实验研究[29-34],LCS源具有准单色、能量连续可调、高极化度、可小型化等特征,是实验室产生XOAM光束的可能方法。在高能领域,有望产生能量为MeV量级的涡旋光束,将有望应用于紧凑型核物理研究探索[35-37]。
本文就利用激光康普顿散射产生波长约为1 nm(光子能量约1.2 keV)的XOAM光束进行了方案设计,1 nm的XOAM光是探究磁性材料的内部磁结构的有力工具。本文简单回顾了圆极化激光与相对论电子碰撞产生涡旋光束的原理并介绍了方案设计,运用解析和模拟的方法对该辐射源的品质进行了预测,并给出了总结。
1 原理与方案设计
1.1 原理
在经典电动力学理论来看,LCS过程将入射激光看作经典的电磁场,电子在穿过激光的过程中会受到洛伦兹力的作用从而产生横向振荡,因为相对论蓝移和相对论多普勒效应,电子的振荡运动会辐射出短波长的X/γ射线。在讨论LCS的过程中,激光强度参数a0是一个非常重要的参数,定义为a0=0.85 × 10-9,其中:λ0为入射激光波长,μm;I0为入射激光光强,W∙cm-2。当a0≤1时,电子在激光场中可假设只受到电场力eE的作用,相应的只有基频辐射产生,称为线性LCS过程。当a0≥1时,电子在激光场中受到的磁场力不能再被忽略,电子在洛伦兹力eE+(e/c)(v×B)的作用下运动,将产生高次谐波辐射,称为非线性LCS过程。LCS的辐射波长[38]可表示为:
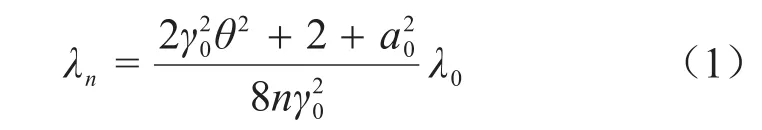
式中:λn为辐射光的n次谐波波长;γ0为电子的洛伦兹因子;θ为辐射光相对于电子运动方向的辐射角,辐射张角为1/γ。由式(1)可以看出,产生波长相同的X射线,LCS所需的电子能量要比第三代同步辐射源所需的电子能量小很多,因此所需的费用也少很多。
电子在穿过圆极化激光时,洛伦兹力的作用会使其产生螺旋形的运动轨迹,其数学表达式为[39]:
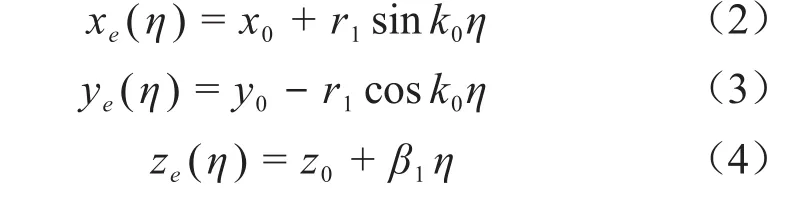
其中:k0=2π/λ0,为入射激光波数;η=ze+ct;x0、y0、z0是电子的初始位置;r1为电子运动轨迹的半径,表示为:
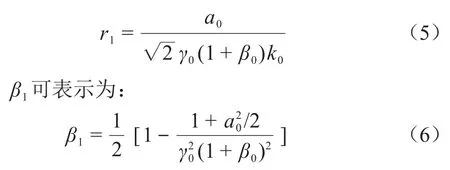
运动轨迹为螺旋形结构的电子产生的辐射能量分布可表示为[27]:
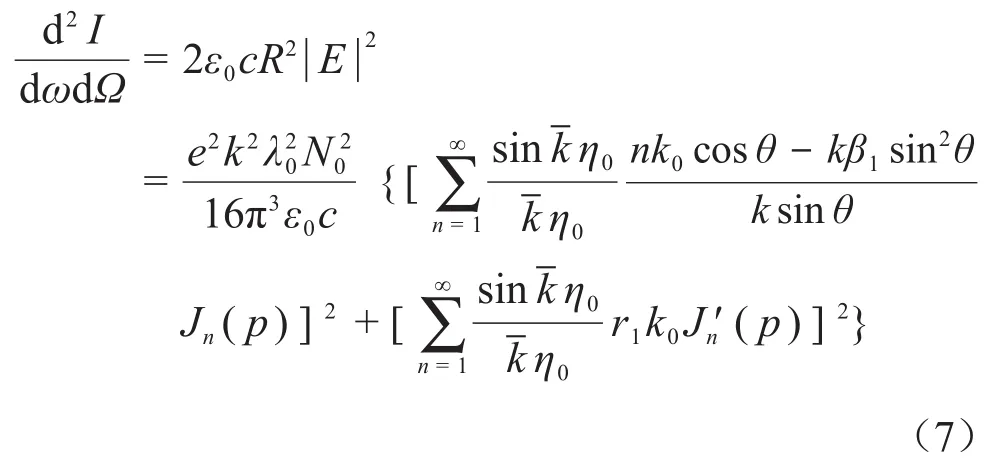
式中:e是单位电荷;ε0是真空介电常数;c是光速,η0=N0λ0/2;N0为入射激光的波周数;p=kr1sinθ;k= ω/c为辐射光波数;k¯=k{1- β1(1+cosθ)}-nk0为辐射光的平均波数;Jn(p)和J'n(p)分别为第一类贝塞尔和第一类贝塞尔函数的一阶导数:

式中:Ne为每秒钟穿过激光的电子数,Δω/ω =1/nN0。式(10)表明:每秒钟的辐射光通量正比于激光的波周数,而带宽反比于激光的波周数,因此长脉冲激光更适合产生高通量、窄带宽的涡旋光束。
1.2 方案设计
鉴于激光康普顿散射源的小型化、准单色、能量连续可调等优点,我们提议发展基于LCS的能量为keV量级的涡旋光束辐射源。我们选择对头碰(激光束与电子束运动方向的夹角为180°)的LCS作用模式,这样的好处是可以增加电子束与激光束的有效作用截面。入射激光选用800 nm的圆极化钛蓝宝石激光器,因为只有圆极化激光与电子相互作用产生的高次谐波带有轨道角动量[27],同时只有当a0≥1时才会发生明显的非线性LCS过程,所以这里选择激光强度参数a=1。根据式(1)可知,产生1 keV的涡旋光束需要的电子能量仅为6.5 MeV,这为实验室提供了开展XOAM实验产生和应用研究的可能。根据式(1)和式(7)对上述参数下的LCS辐射源进行能谱和辐射强度空间分布进行分析,如图1所示,图1(a)为辐射的前6次谐波能谱分布,图1(b)为二次谐波的强度空间分布,强度空间分布呈现环状结构,这是涡旋光束的特征结构。
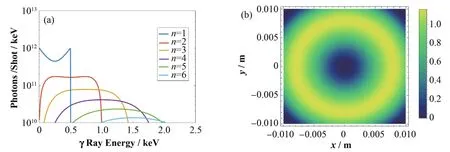
图1 LCS前6次谐波能谱分布(a),二次谐波强度空间分布(b)Fig.1 Energy spectrum of first six harmonics(a),spatial intensity distribution of the second harmonics(b)
需要指出的是,图1是在单粒子模型下的解析解,并没有考虑电子束和激光束的不理想情况,包括电子束能散、发散角、激光带宽等。辐射光的相对带宽受到电子束发射度εn、能散、激光带宽、激光发散角、观察角等影响,可表示为[40]:
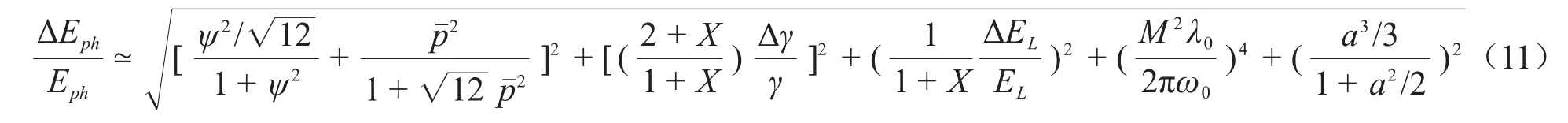
式中:ψ = γθ,表示观察角度;p¯= 2 εn/σx1+X;X=4EeEL/Μ2e,表示相互作用过程中电子的反冲;M为激光束品质因子;w0为激光束的束腰半径。谱密度是评价辐射光品质的重要参数,定义为:
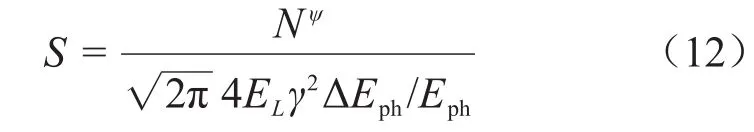
其中:Nψ为观察角内的辐射光通量,定义为:
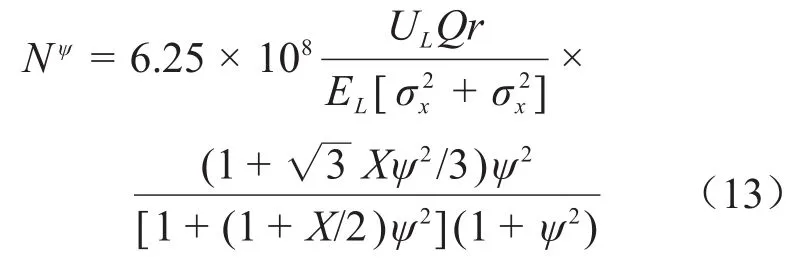
由上面的讨论可知,辐射光通量反比于电子束和激光束的聚焦尺寸的平方,强聚焦的电子束和激光束有利于增加辐射通量,同时,强聚焦激光可以增大激光强度参数,增加LCS的非线性效应,从而增大涡旋光束的通量。但是激光聚焦尺寸的减小,会使得其发散角变大,会反过来降低电子束与激光束的有效作用面积。我们以最大化光谱密度为目标,利用cain模拟软件分析了电子束与激光束聚焦尺寸对谱密度的影响,为了增加电子束与激光束的有效作用截面,宜选择电子束与激光束有相同的聚焦尺寸。采用如表1所示的参数进行模拟分析,可得如图2所示的辐射光谱密度与激光束腰尺寸的关系。

图2 辐射光谱密度与激光束腰尺寸的关系Fig.2 The spectral density of the emitted radiation as a function of the laser beam waist
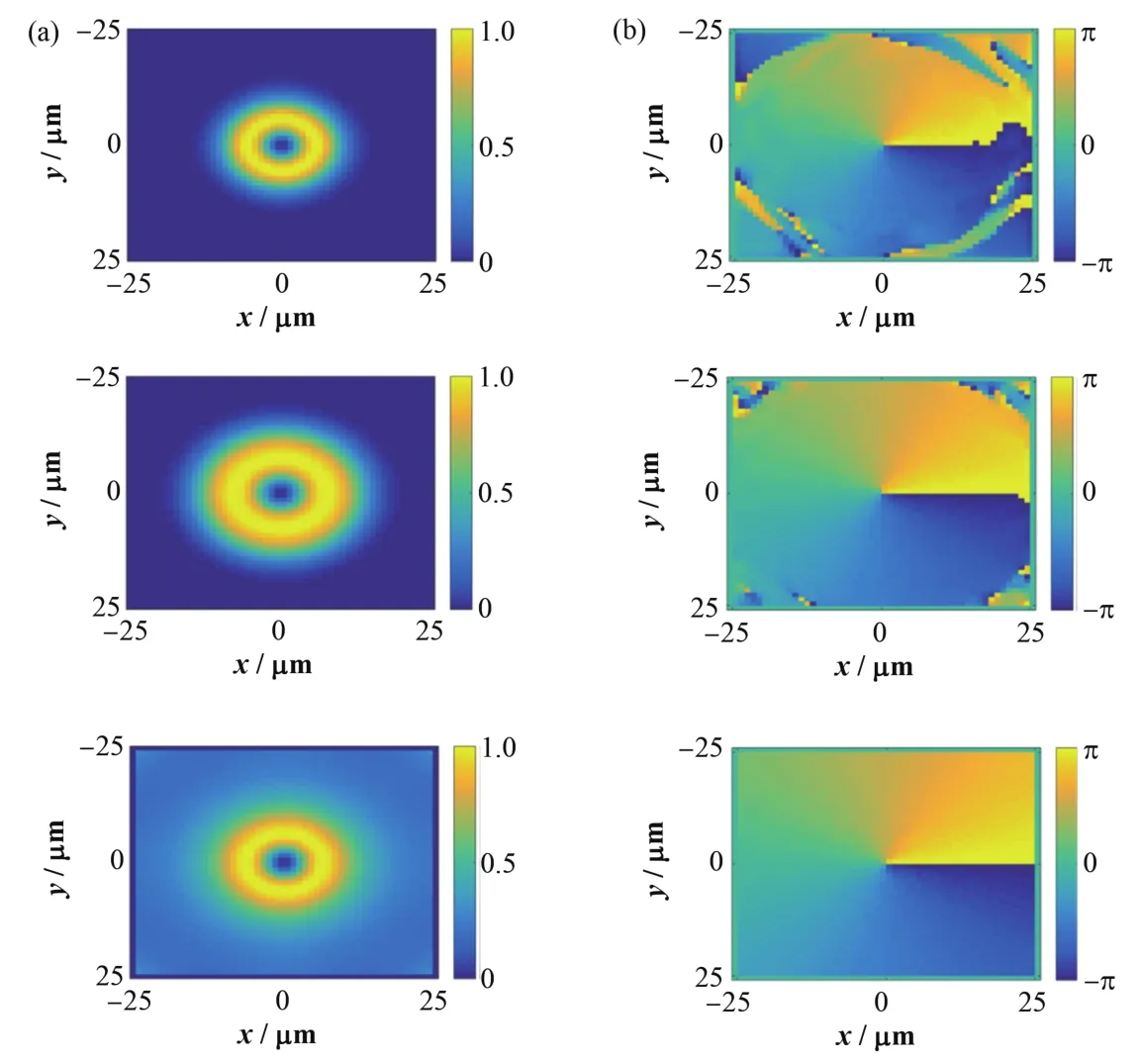
图3 不同脉冲长度下辐射光的强度空间分布(a)和横截面相位分布(b)Fig.3 Spatial intensity(a)and phase(b)distribution of radiation light with different pulse length
根据式(10)可知,为产生高通量、窄带宽的涡旋光束,选用的激光脉冲长度越长越好,但是长脉冲意味着激光能量的增加,我们通过MITHRA[41]模拟软件研究了不同脉冲长度下的辐射光性能,如图3所示。图3(a)是辐射光的强度空间分布,图3(b)是辐射光传播方向上横截面的相位分布。从上到下激光脉冲长度分别为0.1 ps、1 ps和2 ps,相应的激光脉冲能量为0.22 J、2.16 J和4.32 J。图3可以明显看到,涡旋光束的特征,证明激光康普顿散射过程可以产生XOAM光束。同时可以看到,入射激光的脉冲长度越长,横向截面的相位分布越规则,说明辐射光带宽越窄。
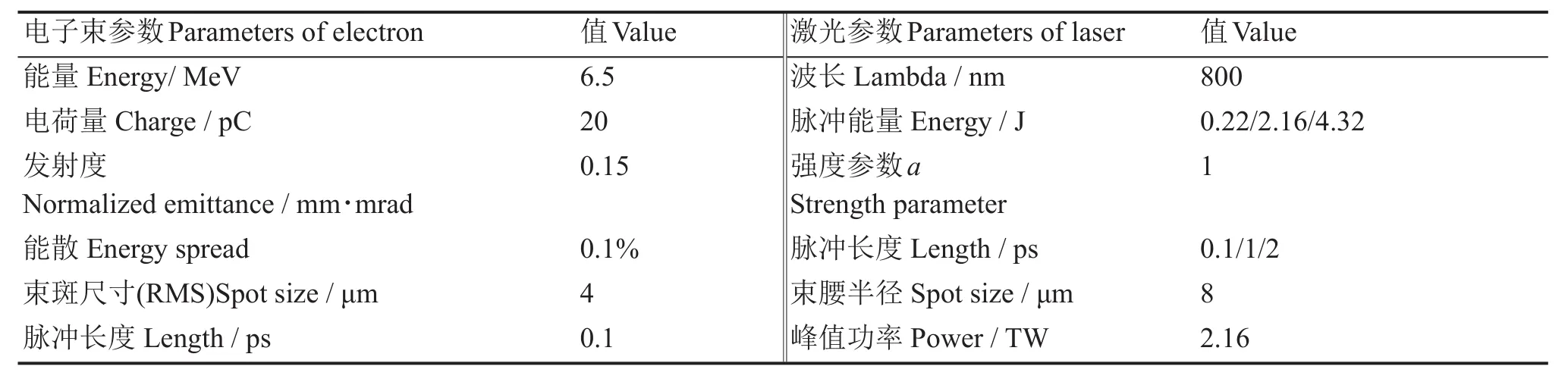
表1 电子束与激光束参数Table 1 Parameters of electron and laser beam
2 结语
本文介绍了一种可小型化的产生能量为keV量级的涡旋光束方案,该方案是利用圆极化激光与相对论电子的非线性激光康普顿散射过程来产生涡旋光束。本文通过解析和模拟的方法对该方案进行了分析。为产生波长约为1 nm的涡旋光束,所需的电子能量为6.5 MeV,这种电子束可以通过注入器、高频高压加速器等获得,造价和占用空间相比于自由电子激光器和同步辐射光源都很有优势,这为实验室开展XOAM光束的产生和应用研究提供了可能。
本文只是一个产生小型化XOAM光束的初步实验提案,还需要在工程和辐射光收集利用等方面进行深入的研究。
