工业机器人可变增益自适应迭代学习控制研究

（西华大学电气与电子信息学院，四川 成都 610039）

工业机器人能代替人类在工业环境中工作，完成单调、繁重、重复的长时间作业，能有效地降低人类的劳动强度，提高生产效率[1－2]。现代工业的快速发展，需要更高质量的产品，这就对工业机器人的轨迹跟踪技术要求越来越高。工业机器人的轨迹跟踪是指通过给定各关节的驱动力矩，使机器人的位置和速度跟踪已知的期望轨迹。当期望轨迹为固定点时为定点控制；当期望轨迹为连续曲线时称为轨迹跟踪控制。

在实际工业生产中，同一轨迹不断重复是工业机器人常见的工作模式。不断重复相同轨迹，使轨迹跟踪的误差会随着重复次数的增加而累积，如何减少误差，这对系统的控制提出更高要求。针对此类问题，迭代学习控制算法应运而生。与其他控制方法相比，迭代学习不需要被控对象的精确数学模型，只需要把之前的控制经验，即控制输入控制误差等信息应用于下一次迭代，通过学习控制算法，使轨迹跟踪误差越来越小，经过有限次迭代之后，实现对期望轨迹的跟踪。

算法的收敛速度一直都是迭代学习算法研究的重点。针对这一问题，学者们采取了一些措施来加快算法收敛速度。文献[3]提出一种反馈变增益迭代学习控制算法，在传统的闭环D 型控制算法基础上，增加了一个变增益反馈控制器，以加快强耦合运行环境下的收敛速度。文献[4]提出了区间可调的变增益迭代学习控制，其收敛速度取决于被控对象、控制律增益、修正指数和学习区间的大小。虽然单纯地引入变增益能显著提高算法收敛速度，但系统可能出现不稳定的情形。采用高阶学习率也能加快算法收敛速度。为此，文献[5]提出了高阶参数优化迭代学习控制算法，该算法釆用之前的多次迭代信息，具有更好的收敛性和鲁棒性；但是，由于涉及到高阶学习率，算法的分析过程比较复杂。文献[6]提出带遗忘因子迭代学习控制最优增益的方法，在迭代学习中引入遗忘因子，根据遗忘因子和系统状态参数计算出系统最优控制增益，实现系统单调快速收敛。然而，遗忘因子的引入会使系统的输出误差不能趋近于零，只能收敛到零点的某一领域内。

近年来，自适应控制、滑模控制、模糊控制等智能控制越来越多地应用到迭代学习控制中，解决了以往单一的迭代算法难以克服的问题。文献[7]将模糊控制与自适应控制相结合，模糊控制用于重新调整PD 型迭代学习控制器的增益，而且新的控制器参数调整更少。文献[8]把滑模控制应用于迭代学习，通过滑模控制来提高系统的鲁棒性，通过迭代学习来改善控制的精度，设计的饱和函数减少了系统的抖振。然而文献[7－8]的复合控制方法并不能解决系统本身的不确定性。

针对工业机器人系统的不确定性，文献[9]研究了自适应迭代学习控制算法，针对参数未知的情况下执行重复任务的刚性机械手的轨迹跟踪，提出了基于PD 反馈结构的控制器，设计了用于应对未知参数的迭代项。文献[10]也提出了一种自适应迭代学习轨迹跟踪算法，通过自适应迭代项克服机器人的未知参数带来的不确定性。它们虽然解决了不确定性问题，但算法的收敛速度还不够快。

为了能在解决系统不确定性的同时兼顾算法的收敛速度，本文设计了指数可变增益，以加快算法收敛速度，并将自适应律部分的误差项定义为广义误差项，同时对位置和速度进行学习，使轨迹跟踪误差更小，系统更加稳定。

1 机器人的数学模型

参考n关节机器人的动力学模型[11]，定义第k次迭代时机器人动力学方程为

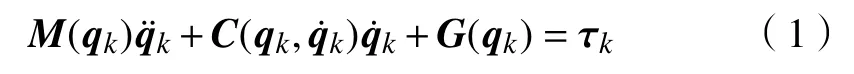
式中：qk、和τk分别为机器人的关节位置、关节速度、关节加速度和控制力矩；M(qk)为机器人的惯性矩阵；C(qk)为离心力和科式力；G(qk)为重力项；下标k∈Z+表示迭代次数。

假设系统满足以下条件[12]。

(A1)任意的t∈[0,T],T为迭代周期，参考轨迹qd有界且二次可导。

(A2)初值满足qd(0)－qk(0)=0，。

机器人动力学方程本身满足以下特性。

(P1)M(qk)∈Rn×n为对称、正定、有界的矩阵。

2 可变增益自适应迭代学习控制算法的设计

本文所设计的可变增益自适应迭代学习算法的思路如图1 所示。控制力矩由PD 反馈控制和参数自适应控制2 部分组成。首先在反馈部分增加指数变增益来加快算法收敛速度，然后在参数自适应部分设计广义误差函数来进一步减小轨迹跟踪误差，增强系统稳定性。

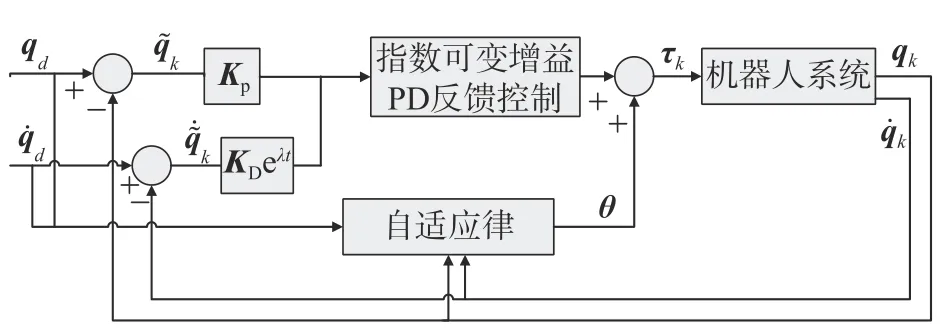
图1 可变增益自适应迭代学习控制算法思路框图

现定义机器人的期望位置qd(t)与实际位置qk(t)的偏差=qd(t)－qk(t)，定义期望速度与实际速度的偏差，定义广义误差函数yk(t)=，Λ∈Rn×n为对称正定矩阵。

所设计的控制器为：

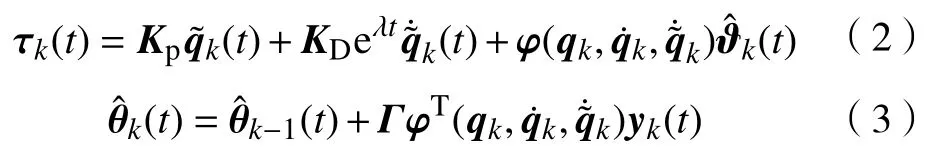
τk前2 项为PD 反馈控制部分，设计了指数变增益 eλt来加快算法的收敛速度。τk第3 项为参数自适应部分，通过设计广义误差函数yk(t)，来对位置和速度共同进行学习，使轨迹跟踪误差更小，增加系统的稳定性。

3 算法稳定性和收敛性证明

取Lyapunov 函数为

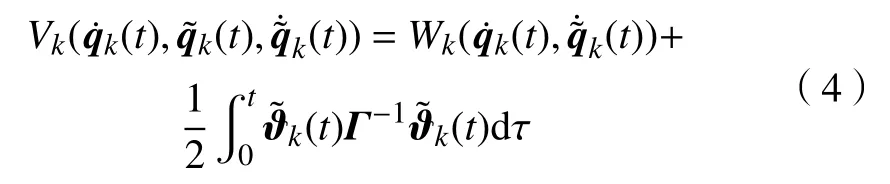
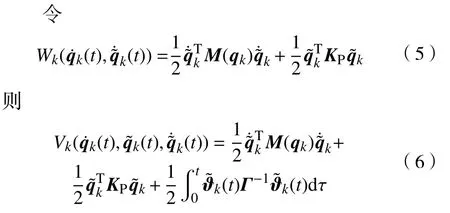
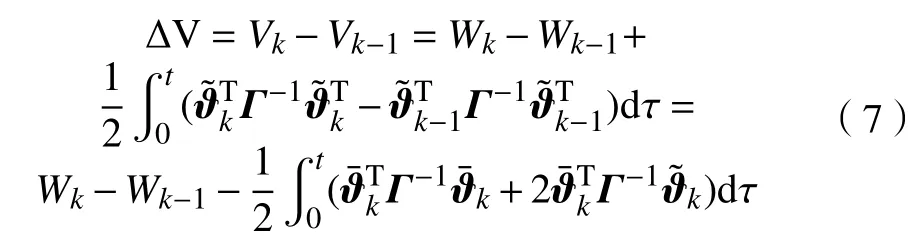
又因为

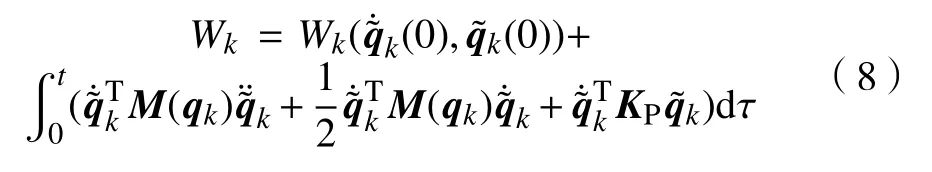
根据式（1）和特性P2、P3 有

将控制率式(2)代入式(9)得

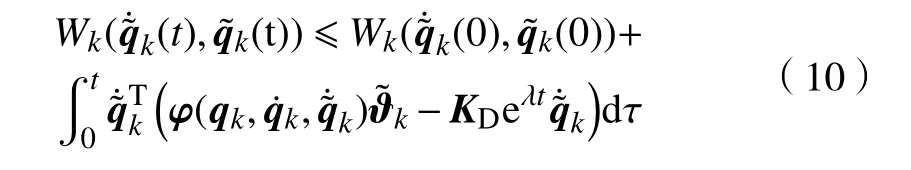
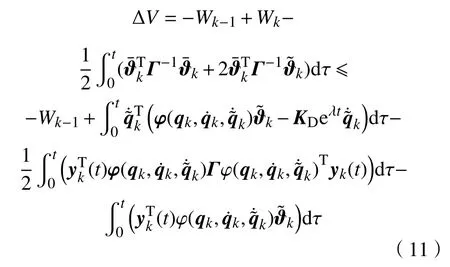
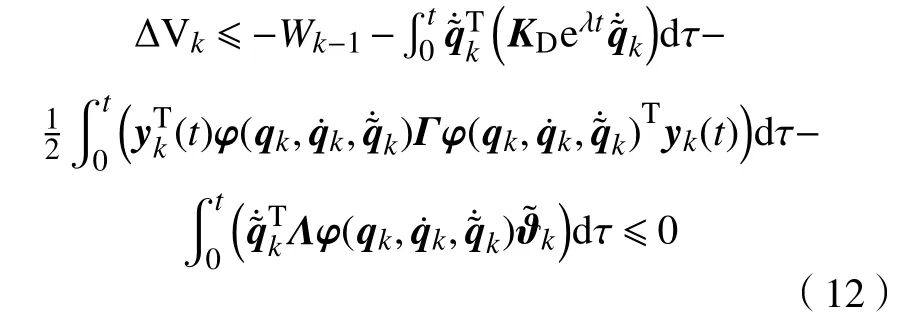
得证Vk为非增函数序列。

将Lyapunov 函数写成递加形式，为

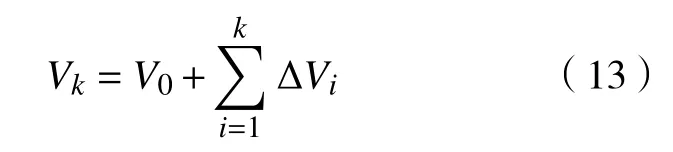
根据式(12)可得

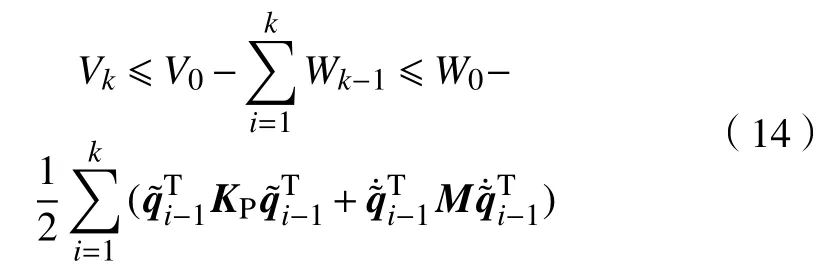
将式（14）移项化简后得

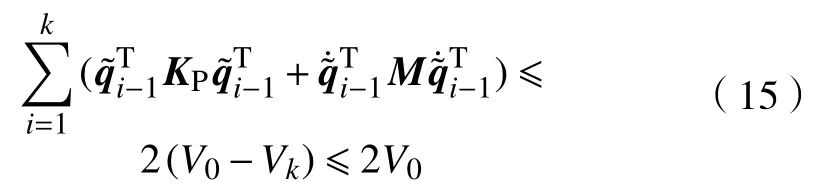
由式（15）可以看出，若想说明Vk有界，须证明V0连续有界，下面证明V0的有界性。

根据假设（A2）有

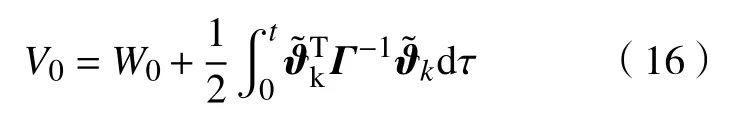
对式（16）求导化简得

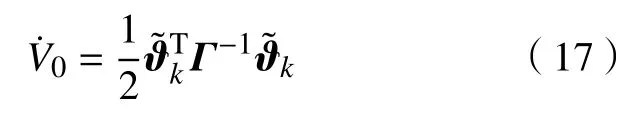
根据基本不等式有

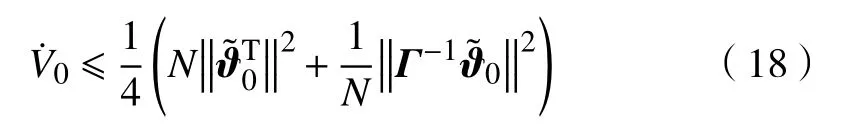
其中N＞0，由拉格朗日中值定理可知V0连续有界，则Vk也有界，又Vk为非递增序列函数，根据以上证明，最终可以得到。

4 仿真

本节选取了Scara 工业机器人[13]为仿真对象验证算法的有效性，并与文献[9]的方法做对比。

如图2 所示，Scara 工业机器人共有4 个关节，由于前2 个关节的质量远大于后2 个关节的质量，因此可将最后2 个关节视为第2 个关节的负载。因此，SCARA 机器人的模型可以简化为二维空间中的双臂机器人系统[14]。

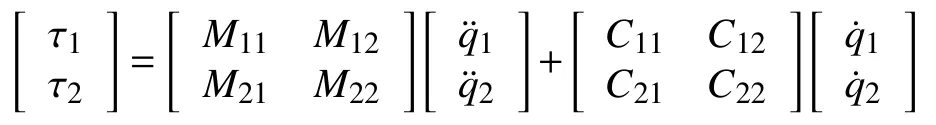
其中，

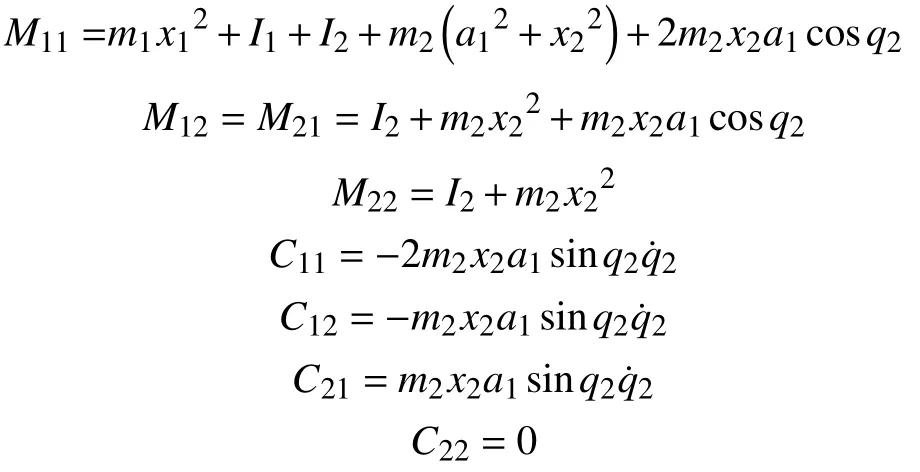
τ1，τ2分别为关节1，2 的力矩，q1，q2为关节1，2的位置，为关节1，2 的速度，为关节1，2 的加速度，m1和m2表示第1 关节和第2 关节的质量，I1和I2为转动惯量，第1 关节和第2 关节的长度和质心分别为a1，a2和x1，x2。具体参数值如表1所示。

图2 Scara 工业机器人结构图

表1 Scara 工业机器人参数

期望轨迹设为

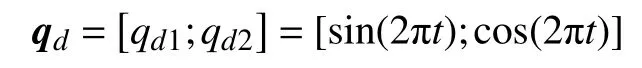
初始状态设定为

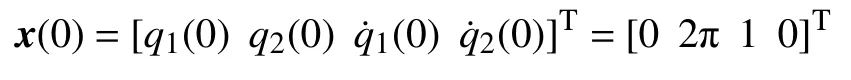
控制器参数取

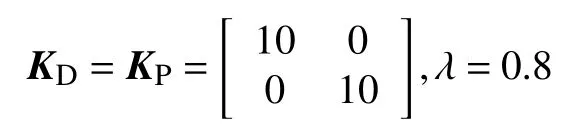
自适应参数取值为

仿真迭代次数总共为5 次，每次时间为1 s。图3—6 示出本文方法的仿真结果，图7—10 示出文献[9]方法的仿真结果。采用本文方法，由图3、图4 可知，机器人的位置跟踪误差在2 次迭代后可以收敛完成，由图5 和图6 可知，机器人的速度跟踪误差在5 次迭代后可以收敛完成。表2 列出了2 种方法收敛完成所需迭代次数、第1 次迭代后的最大误差和迭代完成后的最大误差。

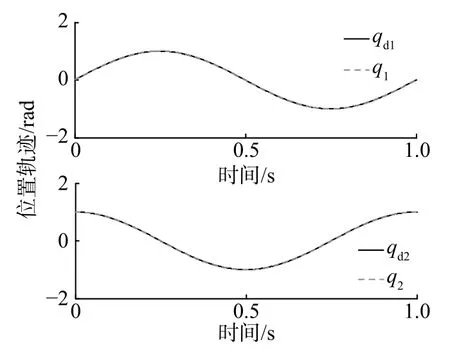
图3 第5 次迭代后的位置跟踪（本文方法）

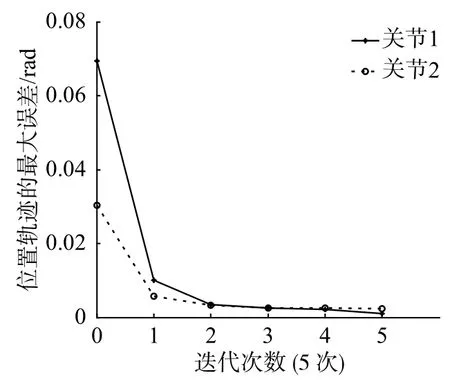
图4 5 次位置跟踪过程最大误差的绝对值（本文方法）

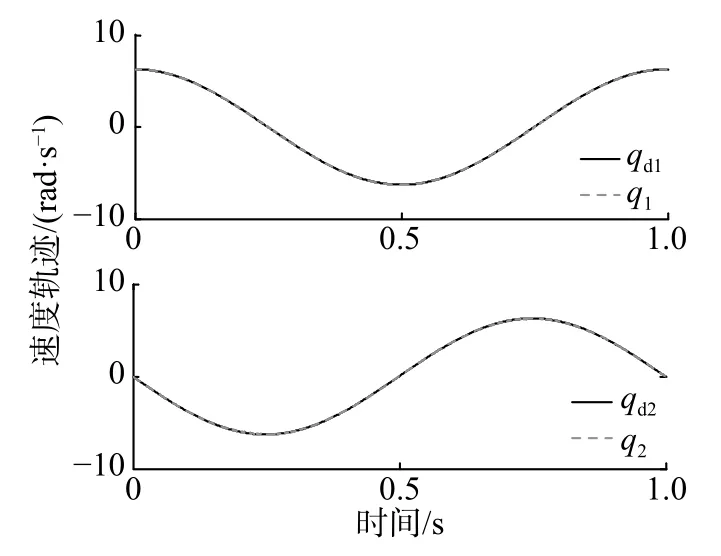
图5 第5 次迭代后的速度跟踪（本文方法）

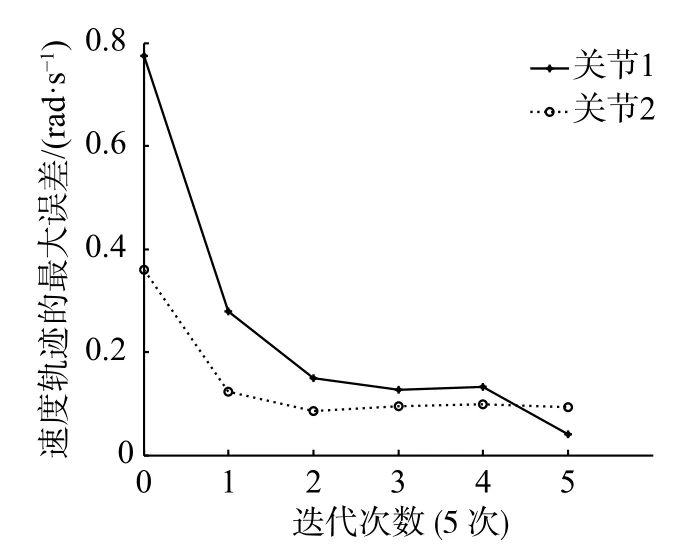
图6 5 次速度跟踪过程最大误差的绝对值（本文方法）

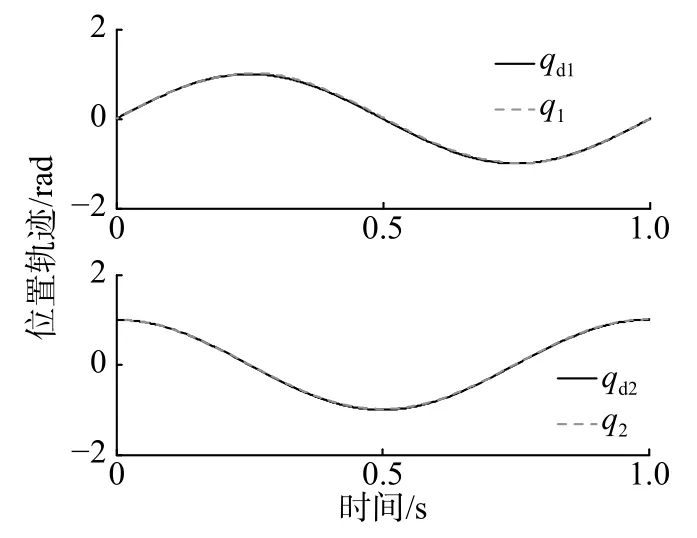
图7 第5 次迭代后的位置跟踪（文献[9]方法）

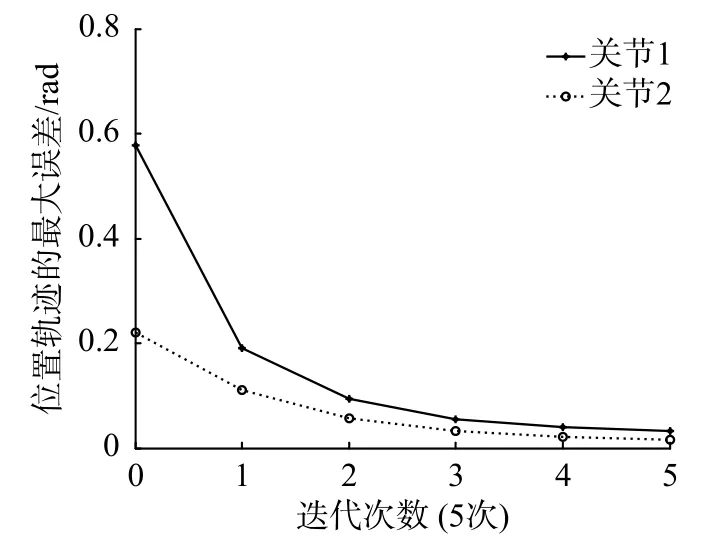
图8 5 次位置跟踪过程最大误差的绝对值（文献[9]方法）

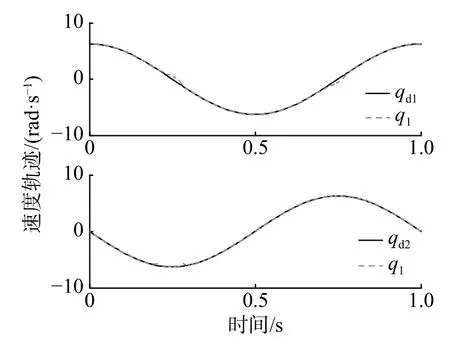
图9 第5 次迭代后的速度跟踪（文献[9]方法）

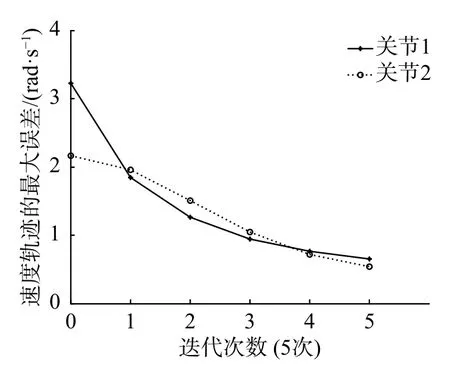
图10 5 次速度跟踪过程最大误差的绝对值（文献[9]方法）

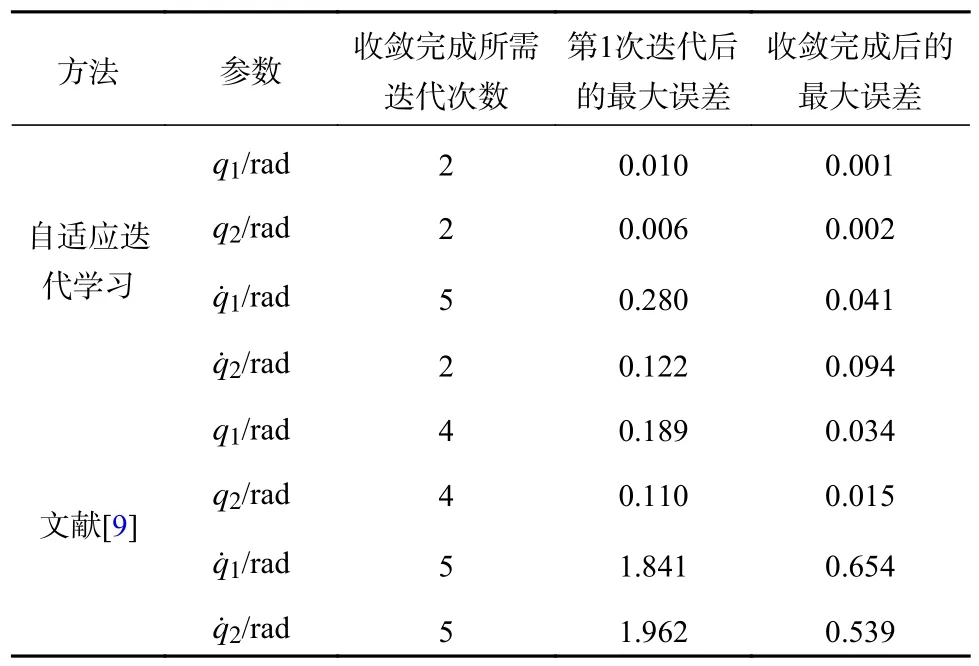
表2 仿真结果对比

由表2 可知：采用本文控制算法，Scara 工业机器人经过1 次迭代后，2 个关节的位置与其期望位置的最大误差为0.010 rad 和0.006 rad，2 个关节的速度与其期望速度的最大误差为0.280 rad/s 和0.122 rad/s，2 个关节的位置跟踪收敛完成需要2 次迭代，收敛完成后的最大位置跟踪误差分别为0.001 rad 和0.002 rad，关节1 的速度跟踪收敛完成需要5 次迭代，收敛完成后的最大速度跟踪误差为0.041 rad/s,关节2 的速度跟踪收敛完成需要2 次迭代，收敛完成后的最大速度跟踪误差为0.094 rad/s；采用文献[9]所述控制方法，Scara 工业机器人经过1 次迭代后，2 个关节的位置与其期望位置的最大误差为0.189 rad 和0.110 rad，2 个关节的速度与其期望速度的最大误差为1.841 rad/s 和1.962 rad/s，2 个关节的位置跟踪收敛完成需要4 次迭代，收敛完成后的最大位置跟踪误差分别为0.034 rad 和0.015 rad，2 个关节的速度跟踪收敛完成需要5 次迭代，收敛完成后的最大速度跟踪误差分别为0.654 rad/s 和0.539 rad/s。综合可知，所提出的可变增益自适应迭代学习控制算法收敛更快，轨迹跟踪的误差更小。

5 结论

本文针对工业机器人的轨迹跟踪问题提出了一种可变增益自适应迭代学习控制算法，采用指数变增益PD 型控制来提高算法的收敛速度，利用自适应算法对系统参数进行估计，设计广义误差函数来减小轨迹跟踪误差，增加了系统稳定性；利用Lyapunov 函数验证了算法的收敛性。与文献[9]的仿真对比结果表明，本文所提的算法收敛更快，轨迹跟踪效果更好。