执行器被攻击下不确定信息物理融合系统的超螺旋控制

陈 勇，李 猛，裴 峥

（1.电子科技大学自动化工程学院，四川 成都 611731；2.西华大学计算机与软件工程学院，四川 成都 610039）

近年来，信息物理融合系统作为大规模复杂分布式系统引起了研究者的广泛关注。它有效地集成了物理单元、通信网络和计算机技术，实现了系统对物理环境的实时感知、动态控制和信息服务。如图1 所示，信息物理融合系统的结构主要分为物理层、传输层和控制层。在物理层中，主要依靠传感器来感知物理环境，并将物理空间中的隐性信息转换为显式数据，然后通过网络将其传输到执行器。执行器主要负责接收数据和执行控制命令。传输层通过有线或无线通信网络传输感测数据和控制命令。控制层通过人机交互融合来自不同系统和环境的数据[1-2]。无论是德国提出的“工业4.0”，美国提出的“再工业化过程”，还是中国提出的“中国制造2025”，这都与信息物理融合系统的研究密不可分。近年来，信息物理融合系统已广泛用于许多领域，例如智能交通[3]、智能电网[4]和云控制系统[5]。然而，随着信息物理融合系统的广泛应用，它也为系统的分析和综合带来了巨大的挑战。主要表现在信息物理融合系统依靠通信网络来实现从传感器到控制器，以及从控制器到执行器的信息传输，其依赖网络传输数据的特性，使其控制系统极易受到网络攻击的威胁。

图1 信息物理融合系统的结构框图

近年来，频繁发生的网络攻击事件敲响了信息物理融合系统安全防御研究的警报。拒绝服务（DoS）攻击和虚假数据注入（FDI）攻击是黑客使用的2 种常见攻击[6－7]。DoS 攻击是一种资源耗尽型攻击。黑客通过发送大量无用的请求以耗尽网络带宽资源，从而中断网络传输，进而导致传输延迟和数据丢失。FDI 攻击旨在破坏数据的完整性，黑客通过注入一些虚假数据或非法篡改传输的数据，以干扰系统的正常运行。文献[8]针对具有DoS攻击的电子物理系统，提出了一种基于分组的状态反馈控制方法。文献[9]研究了信息物理融合系统的输入到状态稳定问题，并考虑了多个传输通道的DoS 攻击。文献[10]针对具有传感器攻击的线性信息物理融合系统，设计了一个新的观测器来防御攻击。文献[11]针对具有间歇性DoS 攻击的非线性信息物理融合系统，提出了一种基于自适应模糊控制的输出反馈安全策略。文献[12]研究了具有虚假数据注入攻击的信息物理融合系统的状态估计问题。文献[13]针对智能电网遭受虚假数据注入攻击的问题，提出了一种应对FDI 攻击的方法。文献[14]研究了广域电力系统中的虚假数据注入攻击，提出了一种基于鲁棒滑模控制的安全控制策略。文献[15]讨论了具有虚假数据注入攻击的分布式滤波问题，为了抵抗攻击，设计了一种基于在线更新的信息保护器。

然而，目前有关信息物理融合系统中的黑客攻击的文献报道还相对较少，关于其安全防御的研究仍处于起步阶段，迫切需要设计有效的安全防御策略，以确保信息物理融合系统的安全和稳定。

滑模控制是一种鲁棒的变结构控制方法。它在处理系统的外部干扰、故障和非线性等问题时表现出了良好的控制性能[16]。文献[17]针对具有不确定性匹配的非线性平面系统，设计了一种新的非奇异终端滑模方法。文献[18]研究了具有执行器/传感器故障和外部干扰的开关网络控制系统，并设计了一种自适应滑模控制方法来处理干扰和故障问题。文献[19]分析了超螺旋滑模控制方法，并设计了一种Lyapunov 方法来证明算法的稳定性。文献[20]在双积分器系统中使用了超螺旋滑模控制方法，并研究了基于输出反馈的稳定问题。

受以上文献分析的启发，本文研究了不确定信息物理融合系统的超螺旋滑模控制。考虑到系统的执行器遭受虚假数据注入攻击，本文计了一种超螺旋滑模控制方法来防御攻击。首先，设计了一种积分滑模函数，并讨论了滑模的稳定性；然后，通过求解线性矩阵不等式来获得滑模参数，并且基于所求解的滑模参数来合成超螺旋控制器；最后，证明了闭环系统的有限时间收敛性。

符号说明：“*”表示对称矩阵中对称项上相应位置的元素；Sym{X}为X+XT；E{·}表示数学期望；‖·‖表示矩阵或向量的2-范数。

1 问题阐述

本文考虑的连续时间信息物理融合系统为：

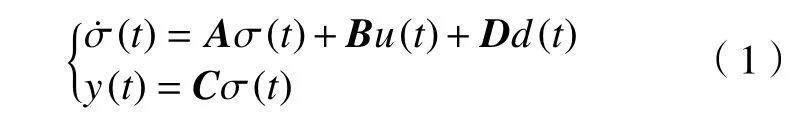
式中：σ(t)∈表示系统的状态；y(t)∈表示测量输出；u(t)∈为控制输入；d(t)表示外界干扰，且d(t)∈L2[0,∞)；A、B、C和D表示适当维数的系统矩阵。

通常，在实际系统中：一方面，温度的变化、系统部件的老化等原因，系统参数会随之发生变化，即参数的不确定性；另一方面，在信息物理融合系统中，黑客可能会给执行器注入虚假数据以干扰系统的正常运行。参数不确定性和执行器被攻击会降低系统的控制性能，使系统不稳定，甚至破坏整个控制系统。图2 给出了具有执行器被攻击的不确定性信息物理融合系统。其中不确定项ΔA(t)被增加到原始系统矩阵A中，同时虚假数据fa(t)被注入到执行器中。

考虑具有参数不确定性和执行器被攻击的信息物理融合系统，系统式(1)可以重新写为：

图2 具有执行器攻击的不确定信息物理融合系统

在本文中，假设攻击数据fa(t)是有界的，即

其中Θ和Υ为2 个给定的矩阵，时变项ϑ(t)满足ϑT(t)ϑ(t)≤I。

针对系统式(2)，本文设计一种控制器来补偿参数的不确定性和执行器被攻击，同时将证明闭环系统的收敛性。

2 设计滑模函数

在本节中，设计了一种积分型滑模函数，并讨论了滑模的动态特性，然后求解出滑模参数。

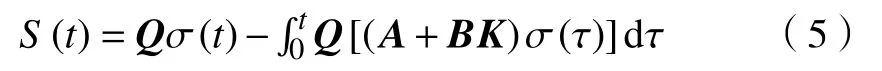
其中K表示待设计的滑模参数矩阵，矩阵Q将被选择使得(QB)－1存在且(QB)－1＞0。对式(5)求微分，得

将等效控制输入式(7)代入系统式(2)中的第1 个方程式，可以得到滑模动态系统，为

其中

接下来，将分析滑模动态式(8)。首先，给出稳定性定义。

定义1系统式(8)是随机稳定的，对于H∞抑制因子ξ＞0，如果下面2 个条件成立。

1)当d(t)=0时，对于任意的初始条件σ(0)=σ0，系统(8)随机稳定的条件是，如果存在1 个常矩阵Φ(σ0)＞0使得式（9）成立。

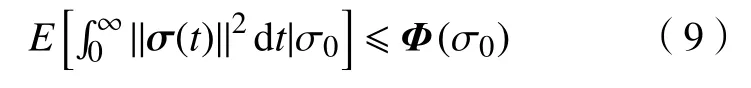
2)对于任意的非零干扰d(t)∈L2[0,∞)，在零初始条件下，也就是，σ(0)≡0，条件式（10）成立。

为了处理参数不确定项ΔA(t)，给出引理1。

引理1[21]如果ϑT(t)ϑ(t)≤I，则存在常数矩阵R和M，以及标量ε＞0，使得

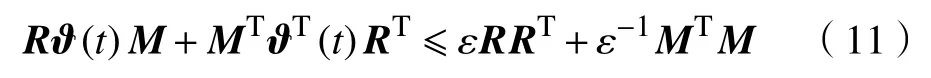
于是，为了分析滑模动态，给出定理1。

定理1当d(t)=0时，滑模动态系统(8)是随机稳定的，如果存在对称矩阵P＞0和矩阵K使得

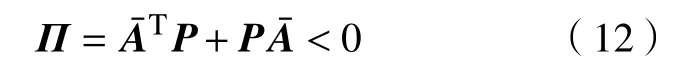
证明首先，构造Lyapunov 函数，为

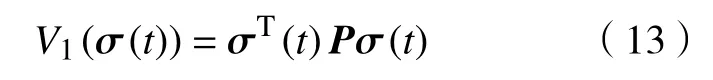
然后，对式(13)求微分，得到

进一步，根据式(12)，可以求得

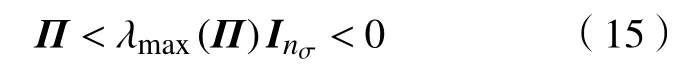
其中λmax(·)表示求矩阵的最大特征值算子，表示nσ维单位矩阵。因此

根据Dynkin 公式，可以推导出

因此，当t→∞时，由式(17)可以求得

其中Φ(σ0)=。

根据定义1，式(18)表明滑模动态在条件d(t)=0的情况下是随机稳定。证明完毕。

接下来，针对干扰d(t)≠0情况，研究H∞抑制性能。

定理2给定标量ε＞0和H∞抑制因子ξ＞0，滑模动态是随机稳定的，如果存在对称矩阵P＞0，以及矩阵T和K，使得

其中

进一步，式(5)中的滑模参数矩阵K可以求解，为

证明定义目标函数为

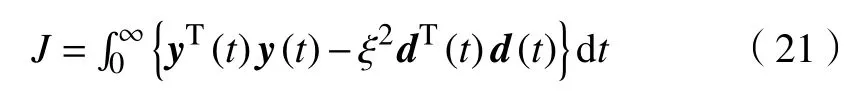
根据定理1，可以得到

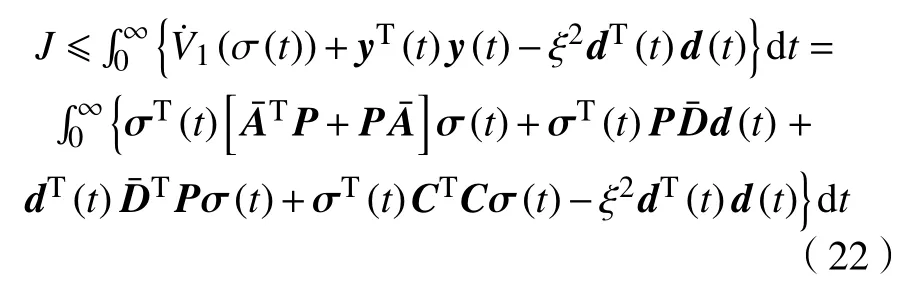
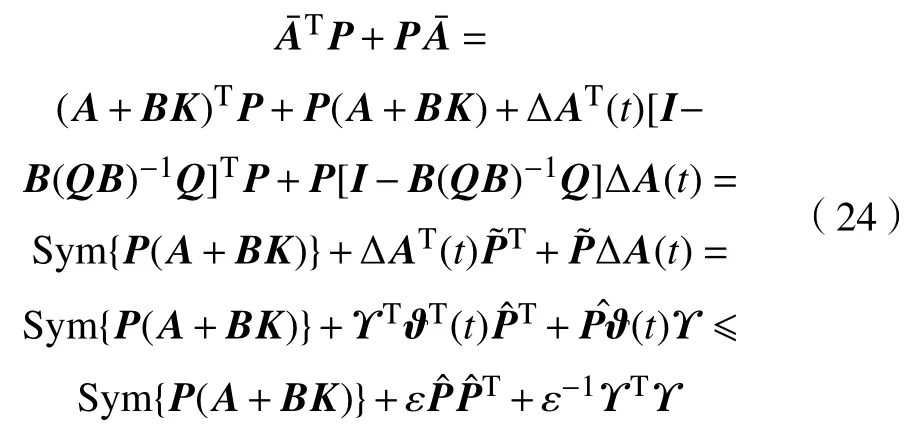
结合式(23)和式(24)，同时使用Shur 补引理，可以推导出

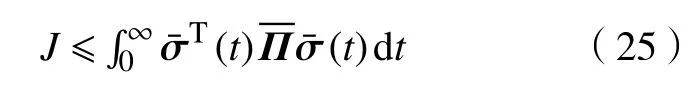
其中

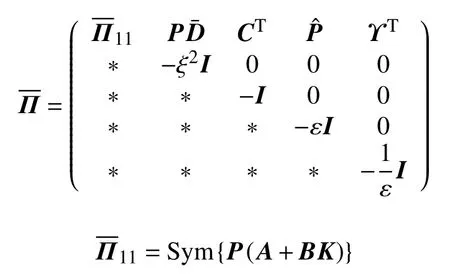
进一步，为了求解式(5)中的参数增益矩阵K，定义变量矩阵：P′=P－1和T=KP′，用矩阵diag{P′,I,I,I,I}左右乘矩阵，可以推导出

使用变量替换，矩阵(26)可以转换成矩阵(19)。证明完毕。

3 控制器设计

在本节中，设计了一种超螺旋滑模控制器，然后证明了闭环系统状态的有限时间收敛性。在设计控制器之前，给出引理2。

引理2[22]对于任意t≥t0，如果存在一个连续函数g(t)＞0使得不等式（27）成立。

其中α＞0，0＜β＜1。则函数g(t)可以在有限时间t*内收敛到原点，且

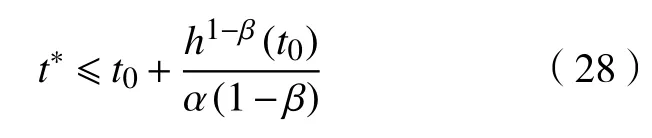
本文中，设计的超螺旋滑模控制器为

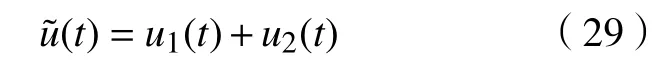
且

其中η1＞0 和η2＞0。

由于执行器攻击fa(t)是有界的，因此下面的假设是合理的。

假设。

对于闭环非线性系统式(30)，给出定理3。

定理3给定标量η1＞0 和η3＞0，对于闭环非线性系统式(30)，如果下面条件成立：

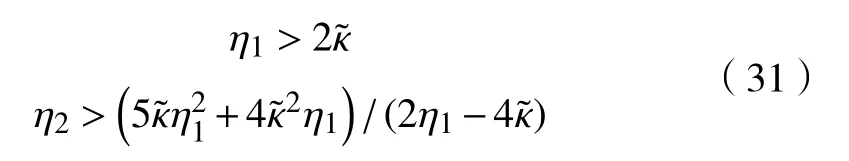
则闭环非线性系统式(30)可以在有限时间内收敛到原点。

证明首先，定义变量=[‖S(t)‖1/2sign(S(t))ρ(t)]。注意到。构造一个矩阵。显然，当η1＞0和η2＞0时，矩阵A0＞0。因此，选择Lyapunov 函数为

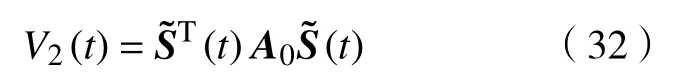
由于矩阵A0＞0，因此，满足条件

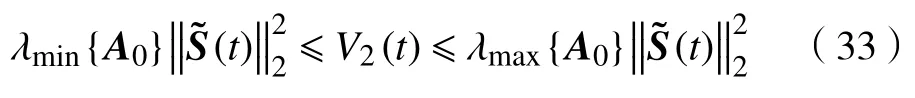
其中λmin{A0}和λmax{A0}分别表示求矩阵A0的最小和最大特征值。进一步，根据文献[19]，对V2(t)求微分，得到

由假设，可以推导出

由式(31)可以推导出A1＞0。因此＜0，也就是，闭环非线性系统式(30)是稳定的。

4 仿真实例

本节采用一个仿真实例来证明设计方法的正确性和有效性。一个线性单连杆机械臂系统[23]为

本文中，机器人手臂系统的参数设置为：=0.2，=5，=1.5，=1.2和=9.8。输出矩阵C=(0 0.4)，干扰增益矩阵D=(0.01 0.1)T，外界干扰为d(t)=0.2cos(t)，参数不确定项为ΔA(t)=Θ0.3·sin(t)Υ，且Θ=(0.01 0.1)T和Υ=(0.01 0.5)，执行器虚假数据fa(t)=0.01cos(t)sin(t)。

控制器(29)中的参数设置为：η1=0.25和η2=0.9，干扰抑制因子ξ=0.18，滑模函数式(5)中矩阵Q设置为Q=(0.4 0.3)使得(QB)－1存在，且(QB)－1＞0。状态的初始设置为σ(0)=(0 0.2)T，仿真时间为10 s，采样周期为0.01 s。通过定理2，可以求解出式(5)中的滑模参数K值，为

图3 示出了开环系统的状态轨迹。可以看出，在没有控制输入的情况下，系统的状态是发散的。图4 示出了闭环系统的状态轨迹。仿真结果表明，尽管系统受到了参数不确定性、干扰和虚假数据注入攻击的影响，在设计的超螺旋滑模控制器下，所有系统的状态依然可以收敛到平衡点。图5 示出了控制输入的轨迹图。可以看出，控制输入可以在3.5 s 左右实现稳定。图6 描绘了滑模面的轨迹图。可以看出，滑模的收敛非常窄，这表明滑模的动态性能很好。

图3 开环系统的状态轨迹

图4 闭环系统的状态轨迹

图5 控制输入的轨迹

图6 滑模面的轨迹

5 结论

本文研究了具有外界干扰和执行器被虚假数据注入攻击的不确定信息物理融合系统的安全控制问题，为了防御攻击，设计了一种新的超螺旋控制方法。首先，设计了一种积分型滑模函数，并分析了滑模动态的稳定性，相应的，通过Lyapunov 函数法求解出了滑模参数矩阵，然后，基于得到的参数设计出了超螺旋滑模控制器，并证明了闭环系统的有限时间收敛性，最后，通过线性单连杆机械臂系统，验证了所设计方法的正确性。仿真结果表明，尽管系统遭受参数不确定性、外部干扰和虚假数据注入攻击，系统状态仍可以收敛到平衡点。