众包服务中基于公平性最大化的团队组建方法

郝 飞，尹小燕，朴斗淳

（1.教育部现代教学技术重点实验室，陕西 西安 710062；2.陕西师范大学计算机科学学院，陕西 西安 710119；3.西北大学信息科学与技术学院，陕西 西安 710127；4.韩国顺天乡大学计算机软件工程系，韩国 忠清南道牙山市 31538）

众包服务作为一种新兴的服务计算范式，为数据传感[1－2]、多媒体优化[3]，图像分类[4]和软件开发[5]等提供网上服务。通常，众包服务流程描述为：解决每个成员可以独立完成的简单任务和在不同阶段需要团队中各成员相互交流解决的复杂任务[6－8]。为了完成众包任务，目前多数研究工作都集中在如何选择合适的移动用户形成团队并完成众包服务上[9－11]，其中，团队组建问题的核心是如何找到一个能够相互交流并协同完成任务的最佳团队。对于给定任务，成员之间“相互交流并协同工作”是有效完成任务的重要方式。已有的团队组建方法的研究大多都集中在基于通信成本最小化的团队组建方法上。

然而，在实际的众包服务中存在避免“相互交流并协同工作”的众包任务，例如目前广为流行的网上项目或标书评审服务。在实际的项目或标书评审中，组织者通常将需要评审的项目或投标建议书分发给评审专家组，在项目或标书评审过程中希望各位专家具有不同的背景或专业知识，各自没有利益冲突，不需要相互交流协同工作，各自在没有任何干扰或冲突的情况下独立地给出评审结论，以保证项目或标书评审的公平性和公正性。可以看出，这类众包任务的团队组建与传统众包任务的团队组建不同：从优化模型的角度来看，传统众包任务的团队组建满足通信成本最小化，而前者的团队组建并不满足通信成本最小化；从信息交流的角度来看，前者的团队组建会使通信成本最大化。通过综合分析众包任务要求以及专家团队与专业知识（技能）的关系，如图1 所示，本文在社交网络环境下，提出一种基于公平性最大化的团队组建方法并用于解决相应的网上众包服务。

1 相关工作

本节主要概述在社交网络环境下和非社交网络环境下的团队组建方法相关研究。

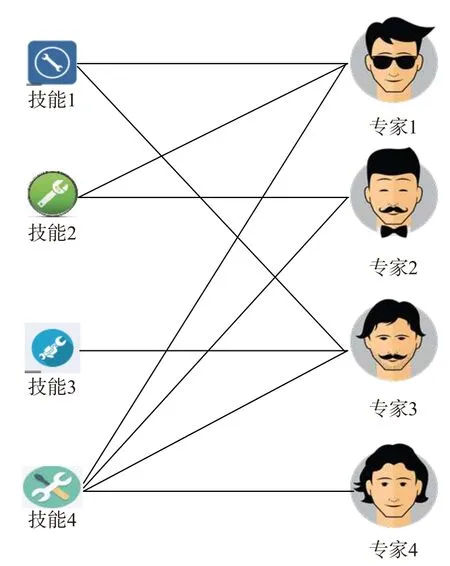
图1 专家团队与专业知识（技能）的关系

1.1 社交网络环境下的团队组建

文献[10]首先提出社交网络环境下的团队组建问题，并证明了团队组建是一个NP 难题，在团队组建方法中将专家之间的社交联系作为选择参数，并借助通信成本最小化设计了Rarest First 近似算法，以寻找一组合适的专家完成团队组建。Majumder 等[12]考虑了每个成员的最大工作能力并以任务负载为约束条件，提出了一种社交网络环境下的团队组建方法。Kargar 等[13]提出了在社交网络中寻找Top-k最佳团队的问题，指出：在实际应用中，用户往往并不满意系统提供的团队组建方案，在许多情况下，用户倾向于对几个备选团队进行比较，然后根据偏好选择最佳团队。据此，Kargar 等设计了一种获取满意解集的近似算法并用于寻找Top-k最佳团队。Li 等[14]将具有相同专业知识的专家集成到一个超级节点中，从而将专家之间的拓扑结构压缩为一个聚类图（或组图），使用聚类分析方法可得到专家的聚类图并据此提出了基于集群的团队组建方法。通过考虑团队组建的成本以及团队成员之间的沟通开销，文献[15－16]提出了一种双目标最优模型，设计了该模型的近似算法并用于解决社交网络环境下的团队组建问题。

1.2 非社交网络环境下的团队组建

理论上团队组建问题可转化为用户分配问题[12]，该问题在运筹学及其应用中已被广泛研究[17－19]。借鉴用户分配问题的研究成果，多数的团队组建方法的研究都使用整数线性规划模型解决团队组建问题，并使用遗传算法[18－19]、分支剪切法[20]等求解整数线性规划模型，从而获得满足条件的团队用于众包服务。通过权衡用户负载和团队规模，Anagnostopoulos 等[21]提出了一种基于负载均衡的团队组建方法，它在多个任务的情况下可平衡专家的工作量。进一步的，通过考虑每个任务的要求及专家之间的协调能力和协作潜力，Anagnostopoulos等[22]设计了一个具有理论保证的近似算法并用于团队组建。通过考虑团队成员的报酬和预期收入，Golshan 等[23]提出了一个面向利润最大化的团队组建方法，并借鉴Greedy-Set-Cover 近似算法，设计了Expert Greedy 和Project Greedy 算法用于非社交网络环境下的团队组建。

与社交网络环境下的团队组建问题相比，非社交网络环境下的团队组建问题不需要考虑成员之间的社交关系。此外，团队组建问题可转化为用户分配问题，非社交网络环境下的团队组建问题可借鉴运筹学中的经典优化模型解决。整体来看，无论是社交网络环境下的团队组建问题，还是非社交网络环境下的团队组建问题，目前的研究多集中在通信成本、成员工作量、任务负荷或利润等最优化方面，笔者还未发现基于公平性最大化的团队组建方法的相关研究。

2 问题陈述

本节首先给出社交图、任务及公平性的形式化定义，然后描述社交网络环境下的团队组建问题。

定义1（社交图） 社交图是社交网络的形式化描述，即为一个二元组G=（V，E），其中，V表示结点（用户）的集合，E表示结点之间的边（社交关系）构成的集合。集合V和E的基数分别为结点V的个数和边E的个数，记为|V|=n和|E|=m。

定义2（众包任务） 在众包服务中，需要完成的特定众包任务T定义为完成T所需的技能集合，即T=(t1,···,tk)。

在众包平台中，专家组由拥有技能的专家构成。每位专家可以拥有几种不同的技能，一种技能也可以被多位专家拥有，专家和技能之间的关系是多对多的关系，如图1 所示。可以看出，每个专家都拥有多种技能，例如：专家3 拥有技能1、3 和4；专家4 只拥有技能4。根据定义2，在众包服务中，众包任务T可描述为T是能完成T的专家组所拥有的技能集合的子集。

定义3（公平性） 在完成众包任务过程中，专家之间的公平性可利用专家技能“相互交流并协同工作”的消费成本定义。即令完成众包任务T的专家组为U′={u1,···,ur}，则专家之间的公平性定义为

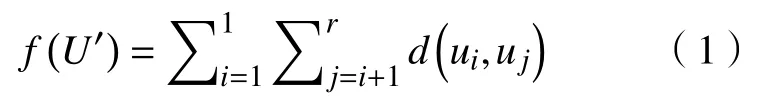
其中d(ui,uj)表示专家ui和uj拥有的技能在共同完成众包任务T的过程中“相互交流并协同工作”的消费成本。

定义3 中，技能“相互交流并协同工作”的通信消费成本越高，在实际中表示专家之间的背景或专业知识差异就越大、利益冲突就越小、独立性就越高。形式地，对于给定的社交网络G=（V，E）和众包任务T，令G中的专家库为U，基于公平性最大化在U中寻找专家组完成众包任务T可描述为如下优化模型：

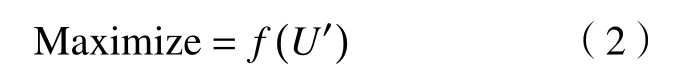
满足

优化模型（2）所组建的团队（或专家组）具有以下2 个特征。

1）可行性。团队中的专家所掌握的技能应满足给定众包任务T的要求，即其中指示专家ui所掌握技能。

2）多元化。所谓多元化是指专家的来源各不相同，专业背景多种多样。以公平性最大化为目标，可在专家库U中寻找来源各不相同、专业背景多种多样的专家组为最优解。从专业知识或技能的角度来看，专家之间的专业知识或技能差距越大，则通信消费成本越高。据此，优化模型可以转换为：

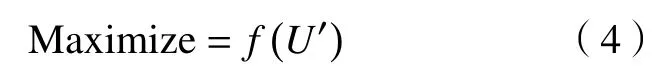
满足

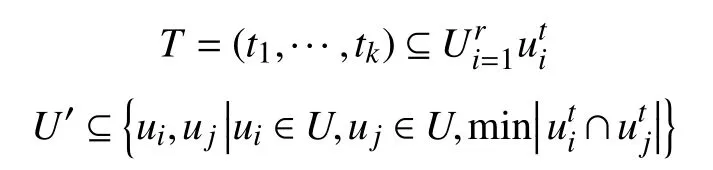
定理社交网络环境下的团队组建问题是NP 问题。

证明考虑社交网络中影响力最大化问题[24－25]，该问题由一个社交网络G=（V，E）和一个参数k（表示种子节点数）定义，其目的是想确定是否存在节点子集S0且|S0|=k将其影响力最大化，即Maxσ(S0)。社交网络中影响力最大化问题是NP 问题。

社交网络环境下组建团队解决由k个技能组成的任务T，目的是找到V的一个子集S0且|S0|=k使得公平性最大化，该问题等价于社交网络中影响力最大化问题，因此，上述定理成立。

引理社交网络环境下基于通信成本最小化的团队组建问题是基于公平性最大化的团队组建问题的对偶问题。

证明显然，基于通信成本最小化的团队组建问题的目标是使通信成本最小化，即

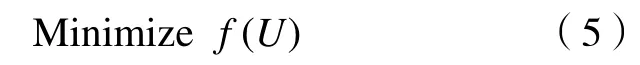
相反，基于公平性最大化的团队组建问题目的是在众包环境中最大化公平性，即

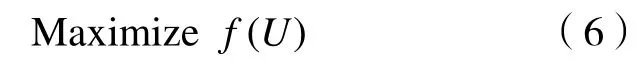
因此，在社交网络环境下，这2 种团队组建问题是对偶问题。

3 基于公平性最大化的团队组建算法

本节中设计了一种新的算法，用于众包任务的团队组建。

3.1 算法

所提出的算法需要一个社交网络G=（V，E）和一个众包任务T=(t1,···,tk)，算法以众包任务T所需的技能作为输入。此外，对于每项技能si都有一组专家具备该项技能si。该算法的输出则是返回满足公平性最大化的专家团队。图2 示出了解决该问题的一个贪心算法。算法工作过程为：初始化“相互交流并协同工作”的消费成本、总成本和最终的专家组（第1—3 行）；然后，将第1 位专家插入团队（第5 行），分别计算第1 位专家与其他专家之间的“相互交流并协同工作”的消费成本。考虑到众包任务的最大公平性原则，该算法始终保留最大消费成本总和。

图2 基于公平性最大化的团队组建贪心算法

3.2 案例分析

假设专家库中有50 个专家，且他们具有评估项目标书的能力，在项目标书评估时各有优缺点。例如用户#8 主要评估来自人工智能和计算机视觉的标书，用户#27 侧重评估项目表述和模糊逻辑方面的标书。对于给定的项目评估，必须从5 方面进行评估，即项目表述、计算机视觉、人工智能、社会计算和数据挖掘。

在本案例中，假设专家对项目表述的评估能力均一致。笔者将基于代价最小化的团队传统组建方法与本文提出的基于公平性最大化的团队组建方法进行了比较，其结果如表1 所示。

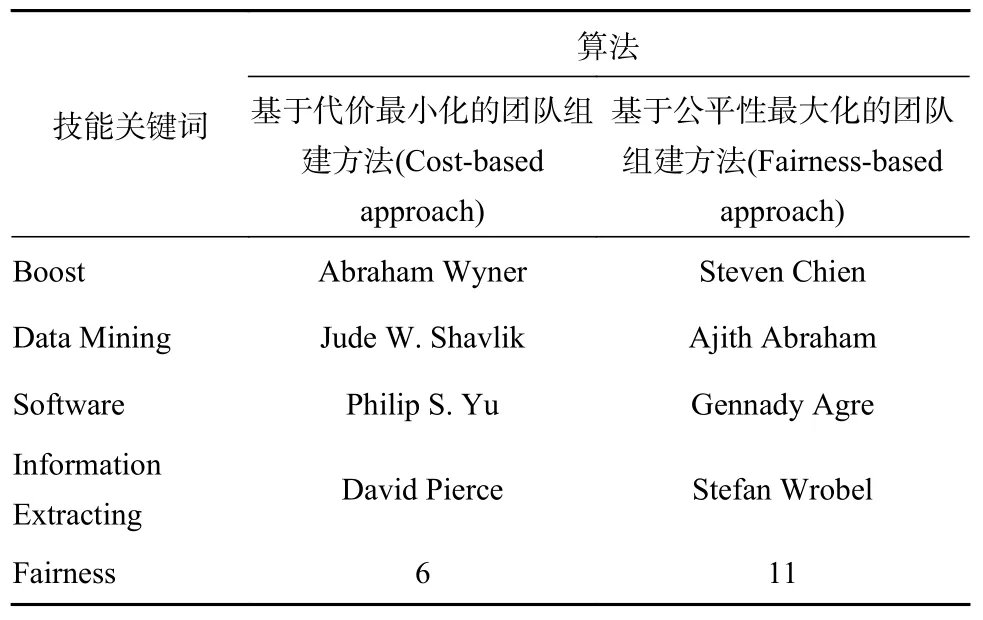
表1 不同算法中众包任务的团队组建结果

1）基于代价最小化的团队组建方法旨在最小化用户之间的通信成本[10]，在任务众包时忽略了公平性功能。

2）基于公平性最大化的团队组建方法用于应对几种特殊情况，例如项目标书评估，为了最大化众包的公平性，考虑了公平性特征。显然，基于算法的公平性可以极大地保证提案评估的公平性。在这种情况下，如果想最大程度地提高任务众包的公平性，那么将提取一个由多元化专家组成的团队，即Steve Chien、Ajith Abraham、Gennady Agre和Stefan Wrobel。

4 绩效评估

本节专门评估所提出的基于公平性最大化的团队组建算法的性能。在公平性方面，将所提算法与先前的工作进行比较。

4.1 ArnetMiner 专家数据集和配置

在本文中，利用关于专家协作的在线公共数据集验证所提出的方法和算法。该数据集可以在http://arnetminer.org/lab-datasets/expertfinding/中找到。具体而言，数据集是一个学术社交网络，研究人员在其中通过有效地交流和研究共享，在若干任务（即论文）上进行协作。因此，该数据集可用于吸引给定项目（例如提案评估）的多元化专家。该数据集包含有关169 个作者（专家）及其合著者（专家）以及其研究主题（技能）的信息，可以用包含1 131 个节点和8 696 个边的社交图来表示，其权重指示通信成本。权重根据其合著论文的数量进行评估。例如，专家Steve Cayzer 与专家David Pearce合著了8 篇论文，与专家Michel Scholl 合著了3 本出版物，而专家David Pearce 与专家Michel Scholl没有任何合作；因此，该协作网络的拓扑结构如图3 所示。其中，成本与权重成反比例关系。为简单起见，使用“A/论文数目”说明这种关系。特别是，专家David Pearce 和专家Michel Scholl 之间没有任何合作交互活动。

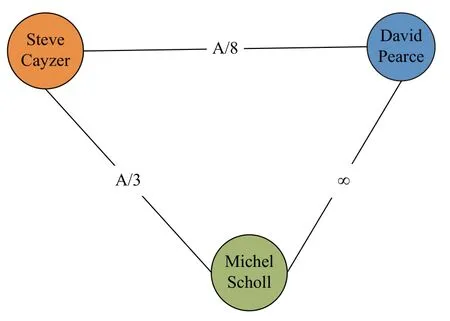
图3 协作网络的拓扑结构

4.2 实验结果

笔者比较了上述2 种算法的性能。通过调整任务中的技能数量从1 到6，获得了不同技能情况下的系统公平性的比较结果，如图4 所示。显然，基于公平性最大化的团队组建方法可以使专家之间的通信成本最大化，与基于代价最小化的方法相比，可以更好地满足系统公平性。因此，可以认为所提方法可用于许多特殊情况，例如通过组建更多具有不同背景且尽可能少的历史社会互动的专家来进行项目表述评估。

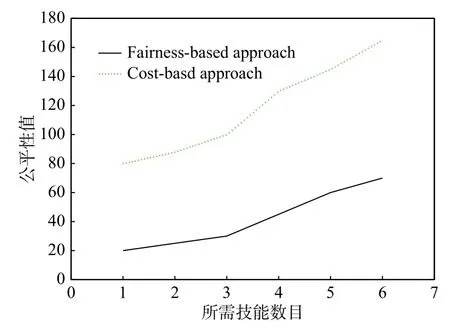
图4 公平性方面的比较结果

5 结论

对于一些特殊的众包应用程序，例如项目标书评估，需要确保任务的公平性。从公平性最大化的角度出发，本文聚焦在一个新颖的团队组建问题上，即选择多元化的专家作为团队，从而使专家之间的“相互交流并协同工作”的消费成本最大，并形式化证明了提出的问题是传统团队组建问题的对偶问题。为了解决团队组建的对偶问题，本文首先定义了通信成本总和，以刻画系统公平性，然后提出了基于公平性最大化的团队组建新问题，并鉴于该问题是NP 难问题，进一步设计了贪心近似算法，贪婪地选择可以满足可行性和多样化重要特征的专家对。此外，通过案例分析，揭示了所提出方法的可行性。