航空轮胎动态印痕及驻波仿真计算

付新华，荣英飞，刘肖英，黄艳军，胡永康

（三角轮胎股份有限公司，山东 威海 264200）

航空轮胎分析、设计和制造过程中关注的重点问题是航空轮胎的动态印痕、双倍负荷和驻波等高速条件下的力学性能。航空轮胎在飞机起飞和降落时承受的负荷较大、速度高，且速度变化0～400 km·h-1在很短时间内完成，因此实验室常规设备很难完成相关测试。

Abaqus软件提供了Standard和Explicit两种算法，两者的区别在于数学求解方式不同。隐式分析用Newton-Raphson算法求解平衡方程，而显示分析采用中心差分法对运动方程积分进行求解，相比而言Abaqus/Explicit算法更适用于动态问题的分析。

本工作以我公司设计的某规格航空轮胎为例，探讨采用Abaqus/Explicit算法计算航空轮胎在不同工况下的动态印痕和驻波仿真的方法。

1 计算流程

首先在Abaqus/Standard下完成二维充气和三维充气计算，然后调用该三维充气结果应用于Abaqus/Explicit方式进行动态加载和滚动计算。

Abaqus/Explicit算法计算时对网格划分、单元类型、材料定义等与Abaqus/Standard定义不同。

1.1 网格划分

Abaqus/Explicit算法计算成本与单元数目成正比，且大致与最小单元的尺寸成反比。因此用Abaqus/Explicit算法计算中模型网格划分时尺寸应尽量均匀划分且保证形状规则，若模型中有个别单元尺寸很小或者形状很不规则，会降低模型的稳定性极限，导致计算时间延长、仿真结果精度降低。

1.2 单元类型

Abaqus/Explicit算法不能假设材料的完全不可压缩，由于不可压缩材料具有无限大的波速，会导致时间增量步为零而导致无法计算，因此H单元不能用于显式计算中，本工作计算时胶料选择线性缩减积分单元CGAX4R和CGAX3。

由于线性缩减积分单元存在来自于本身的沙漏数值问题而过于柔软，加之选用Abaqus/Explicit算法时网格一般较粗，这些因素会让零能模式通过网格进行扩展，进而可能导致计算结果很差。Abaqus中可以通过“沙漏刚度”设置来限制线性缩减单元沙漏模式的扩展。

2 动态印痕调试计算

2.1 有限元模型

将航空轮胎进行网格划分，选择Abaqus/Explicit算法适合的缩减积分单元、定义可压缩性并进行沙漏刚度设置，橡胶材料超弹性选用Yeoh本构模型，粘弹性由时域7阶Prony级数表征，综合信息得到的二维有限元模型如图1所示。二维有限元模型有1 845个单元、1 980个节点。均匀划分180Sectors旋转生成三维有限元模型，如图2所示。三维有限元模型有331 921个单元、356 221个节点。其中胶料单元平均尺寸为6.37 mm，最小尺寸为3.37 mm；骨架单元平均尺寸为6.26 mm，最小尺寸为5.06 mm。

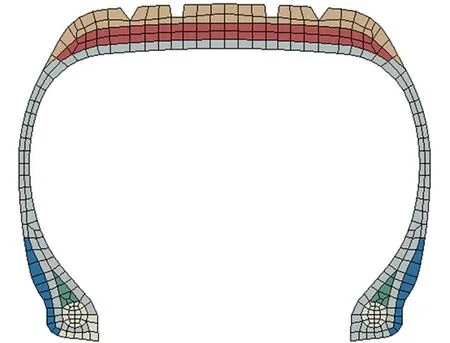
图1 轮胎二维有限元模型

图2 轮胎三维有限元模型

2.2 加载工况

轮辋接触处摩擦因数设为0.3，胎面与地面接触处摩擦因数设为0.8，加载工况为900 kPa/5 000 kg和1 500 kPa/20 870 kg。

首先在Abaqus/Standard下完成上述两种工况的二维充气和三维充气分析，然后在Abaqus/Explicit下进行加载和滚动计算。

2.3 显式计算

显式计算文件包括模型信息、路面、转动惯量设置、Amplitudes设置、边界约束及结果输出等部分。

2.3.1 导入及路面、轮辋定义

首先导入模型中胶料和骨架集合；模型中建立的单元和节点集合以及接触面集合等信息并重新定义三维充气表面、接触面等信息，定义路面、轮辋参考点及其质量和转动惯量。

2.3.2 幅值及分析步设置

定义AMPLITUDE，本次计算用到Constant，Smooth step和Tabular等AMPLITUDE设置，分别用于充气、加载和速度等。

Abaqus/Explicit算法计算时，时间步长对显式计算有很大的影响，在Abaqus中提供了由模型最小单元尺寸限制时间步长的方法（默认）。此外，Abaqus/Explicit算法可以自定义设置时间步长，自定义的时间步长太大或太小都有可能导致误差持续积累，进而造成计算结果精度降低[1]。如果模型中网格尺寸均匀，一般选择默认时间步长即可。

计算时先对路面参考点完成加载之后再进行速度设置，速度从0加速到40 km·h-1后以该速度稳定滚动1 s。

2.3.3 动态印痕结果

两种工况按上述设置以40 km·h-1的恒定速度滚动1 s得到的轮胎动态印痕如图3和4所示。

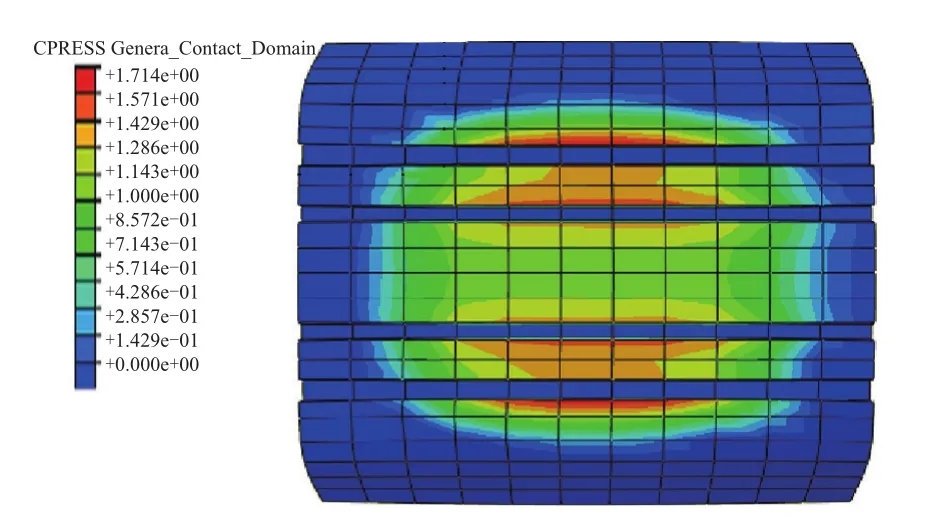
图3 900 kPa/5 000 kg工况下轮胎的动态印痕

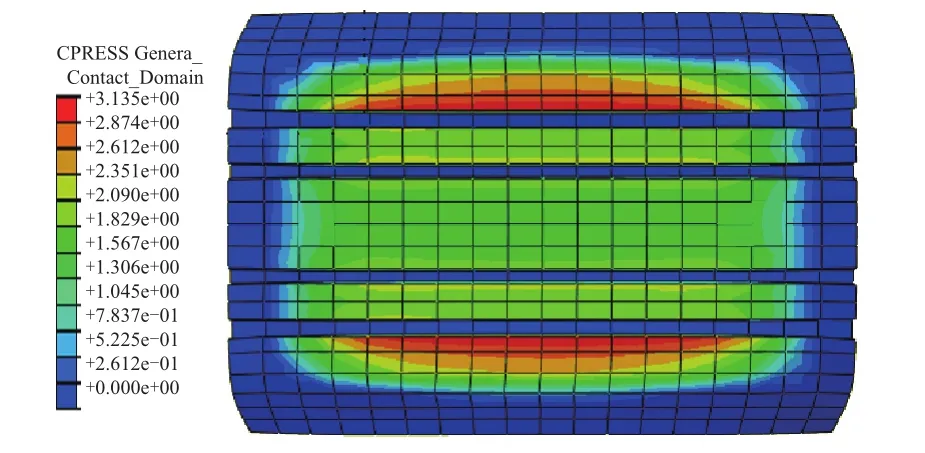
图4 1 500 kPa/20 870 kg工况下轮胎的动态印痕

900 kPa/5 000 kg工 况 下 行 驶 速 度 为40 km·h-1时的轮胎能量对比如图5所示。从图5可以看出，计算模型中的伪应变能远小于应变能，约占内能的9%，因此可以将模型中沙漏造成的影响近似忽略。

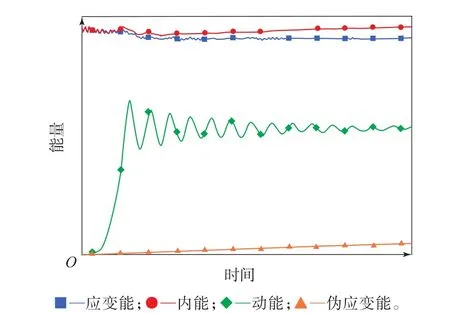
图5 轮胎的能量对比

3 高速驻波

由于轮胎骨架材料与胎冠存在夹角，轮胎存在一个临界速度，当轮胎达到这个临界速度时就会出现驻波，而橡胶材料的滞后特性会加大驻波的影响。发生驻波时轮胎胎面会产生明显的波形，最大的波峰出现在接地后区域并且沿轮胎周向逐渐衰减。驻波现象会导致轮胎变形增大、温度急剧上升，从而导致轮胎材料性能急剧下降，使轮胎在很短时间内被破坏[2]。由于飞机起飞和着陆瞬间速度很大，因此航空轮胎在设计时要考虑驻波及临界速度。

3.1 计算设置

按照GB/T 9747—2008《航空轮胎试验方法》模拟航空轮胎起飞试验工况：加载时间为0.4 s，之后用4 s将速度从0线性增大到400 km·h-1。因此计算时分为两个步骤。步骤1只充气和加载，步骤2计算速度由0增大到400 km·h-1的过程，通过模拟该工况尝试找到临界速度。

3.2 计算结果

行驶速度为272，309，361，400 km·h-1时轮胎（橡胶材料考虑粘弹性）侧向位移分布见图6—9。

图6 272 km·h-1速度下轮胎侧向位移分布

图7 309 km·h-1速度下轮胎侧向位移分布

图8 361 km·h-1速度下轮胎侧向位移分布

图9 400 km·h-1速度下轮胎侧向位移分布

行驶速度为309和400 km·h-1时轮胎仅考虑超弹性时（橡胶材料未考虑粘弹性）侧向位移分布分别见图10和11。

图10 309 km·h-1速度下轮胎仅考虑超弹性时侧向位移分布

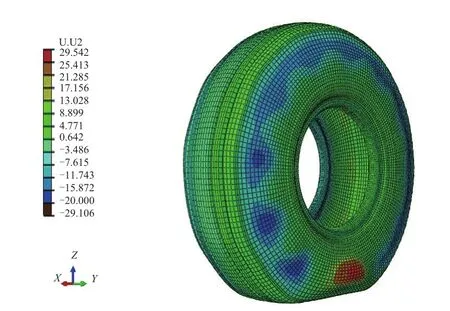
图11 400 km·h-1速度下轮胎仅考虑超弹性时侧向位移分布

从图6—9可以看出，272 km·h-1时轮胎未发生驻波，在309 km·h-1时轮胎有轻微驻波出现，随着速度的增大，轮胎的驻波现象愈加明显。

从图10和11可以看出，在相同速度下，仅考虑橡胶材料的超弹性时轮胎的驻波程度比有粘弹性参数时驻波程度明显减弱。这也印证了粘弹性设置对动态计算，尤其是速度较大时的动态计算结果有很大的影响[3-4]。

此外，将上述模型中胎面胶模量提高25%，其他设置不变，发现400 km·h-1时轮胎变形程度减弱，说明提高胎面胶模量可以提升轮胎的临界速度。

4 结语

应用Abaqus/Explicit算法计算不同工况下航空轮胎的动态印痕和高速滚动驻波的方法可以用来模拟计算测试设备难以实现的测试，为航空轮胎设计提供相关数据支持；采用Prony级数表征橡胶材料粘弹特性，计算结果表明粘弹性设置对航空轮胎高速动态分析有显著影响。