GF(2m)域ECC 点乘算法优化设计*

刘金龙，张玉婷，王 尧

（海军参谋部，北京 100841）

0 引言

无线传感器网络（Wireless Sensor Network，WSN）是由一种分布式、自组织的Ad hoc 网络，但有别于传统的Wireless Ad hoc 网络。WSN 节点由能量有限、计算和存储能力小、具有数据采集功能的传感器节点组成。随着传感器节点资源的升级和某些传感器网络应用的高强度安全需求，非对称加密算法已被广泛研究[1]。椭圆曲线密码算法（Elliptic Curves Cryptography，ECC）因为自身的安全强度高、密钥长度短、存储和带宽要求低等优点[2]，特别适用于WSN 等资源受限的领域。而在ECC 密码体制中，椭圆曲线的点乘运算（Q=kP）是算法安全性的关键，占了整个运算的很大比例，决定了算法的执行效率[3]。因此，研究有限域内点乘运算的优化实现具有重要的意义。

考虑到硬件实现的特点，本文以二进制域的椭圆曲线密码方案为研究重点，在权衡资源消耗与运算速度的基础上，设计了串并混合的点乘运算整体结构，并实现底层有限域的模加、模乘、模平方和模逆运算的轻量化改进和电路结构设计，最后在FPGA 平台上进行仿真验证。结果表明，方案的点乘运算效率得到了明显提升。

1 椭圆曲线密码基础

1.1 椭圆曲线的定义

定义在二进制域GF(2m)的椭圆曲线可表示如下：

其中a,b∈GF(2m)，且b≠0，除了式（1）所确定的所有点(X,Y)外，还包括一个特殊的点即无穷远点。在实际应用中，为避免一些复杂的运算，椭圆曲线上的点通常用其他坐标系表示[4]。在标准射影坐标下的点可表示为(X,Y,Z)，Z=0 表示无穷远点，Z≠0 时相互之间的转化关系为x=X/Z、y=Y/Z。

1.2 椭圆曲线上点的运算

椭圆曲线上所有的点的集合外加上无穷远点和椭圆曲线上的加法运算构成一个加法群[5]。在GF(2m)域内，令E为式（1）所表示的曲线，P=(x1,y1)，Q=(x2,y2) ∈E，R=(x3,y3)=P+Q，则P、Q两点相加的运算规则如下。

（1）当P≠Q时，点加运算：

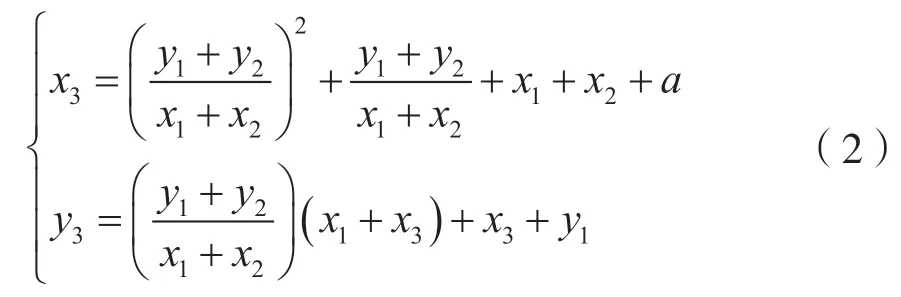
（2）当P≠Q时，点加变为倍点运算：

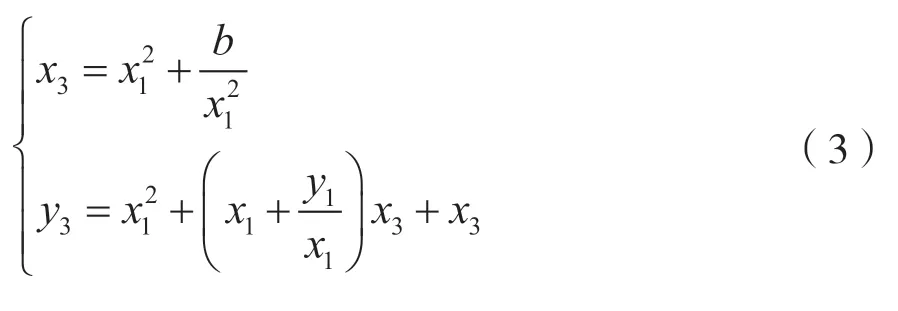
1.3 椭圆曲线密码体制的运算层次

点乘运算在椭圆曲线加密体制中的作用如图1 所示。最上层为协议层，通过调用点乘运算实现ECC 加解密和数字签名；之后为群运算层，通过调用点加和倍点运算实现点乘运算；最底层为域运算层，包括多种有限域模运算，是实现点加和倍点运算的基础[6]。因此，实现椭圆曲线点乘运算的高效设计需要针对不同运算层次的特点进行针对的优化设计。

图1 椭圆曲线加密体制的运算层次

2 有限域模运算优化设计

有限域内的模运算是点乘运算实现的基础，是影响点乘运算效率的关键。下文分别对GF(2m)域上的模加运算、模平方运算、模乘运算和模逆运算进行优化设计。

2.1 模加运算设计

有限域GF(2m)域内的加法相对简单，可以通过将表示模加元素的二进制序列进行逐位异或运算来完成。

它对应的硬件电路可用m个异或门实现，如图2 所示。

图2 模加单元电路结构

2.2 模乘运算设计

模乘运算是影响点乘实现效率的关键，包括多项式相乘和取模两步，而多项式相乘部分的计算周期较长，分为并行和串行两种类型。有限域GF(2m)并行结构乘法器的硬件复杂度为m2，它的面积和功耗随m的增加而增加。在硬件实现时常用串行模乘算法，虽然该算法的计算周期较长，但是其实现面积和功耗最小[7]，比较适合无线传感器网络这种资源受限的环境。本文采用一种优化的LSB 串行模乘算法，如下：

算法在每次循环中完成两次异或和两次移位操作，对于硬件实现来说很方便，而且不需要占用任何逻辑单元。通过对A的移位操作，通过A值是否为0 进行判断，确定算法是否结束。当A的高位有多个0 时，算法的运算效率会显著提高。另外，算法中的移位和判断操作对算法的运算效率影响很小。

模乘单元的硬件电路结构如图3 所示。

图3 模乘单元电路结构

2.3 模平方运算设计

在有限域GF(2m)内，模平方运算可以用模乘来实现。但是，由上文可知，模乘运算的计算周期较长且硬件电路设计复杂。因此，本文利用有限域GF(2m)下模平方运算的特殊性，采用一种基于多项式平方的快速模约减算法，通过预计算的方式，牺牲算法的灵活性，达到提高计算的效率并减少资源消耗的目的。

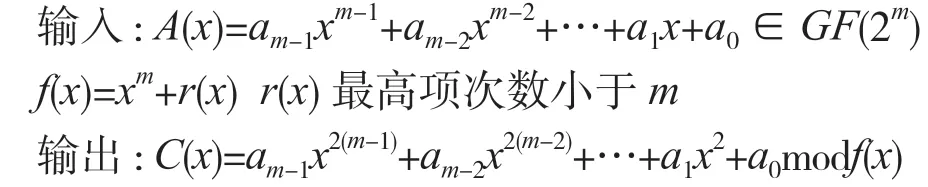
对约减多项式f(x)进行取模时，根据xm=r(x)modf(x)，将A2(x)中次数高于m-1 的多项式元素转化为低于m位，再把结果在同一位的所有值进行异或。在固定的约减多项式下，通过预计算，模平方运算可在一次异或运算时间内完成，且所用的资源不超过m个异或门。

针对特定的m≤233 与f(x)=x233+x47+1，对应的组合逻辑电路设计如图4 所示。

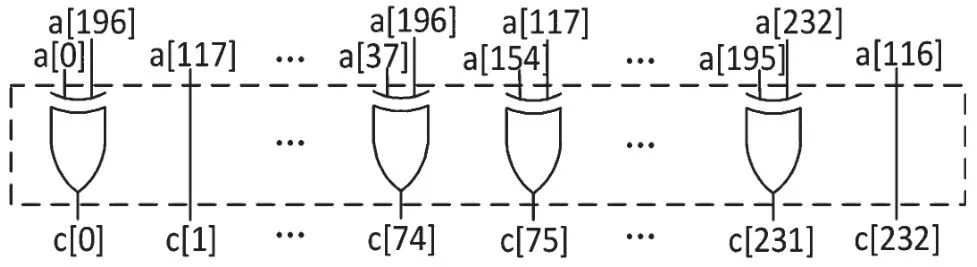
图4 GF(2233)域下模平方单元结构

2.4 模逆运算设计

模逆运算是有限域运算中最复杂也是最耗时的。GF(2m)域上的求模逆算法有两种——基于扩展Euclideam 算法和基于Fermat 小定理的算法[8]。前者通过判断、移位和异或来实现模逆运算，实现比较简单，但是需要增加单独的模逆运算模块，大大增加了整体面积；而基于Fermat 小定理的模逆算法是将有限域的逆运算转换为模幂运算，可以通过调用模乘和模平方来实现，算法如下。

可以看出，一次模逆运算需要m-2 次模乘和m-1 次模平方。尽管这样，一次模逆运算的计算效率还是较低。而由前文可知，模乘运算的计算复杂度比模平方复杂得多，本文采用Itoh-Tsujii 算法[9]改进运算，以减少模逆运算中的模乘运算次数。

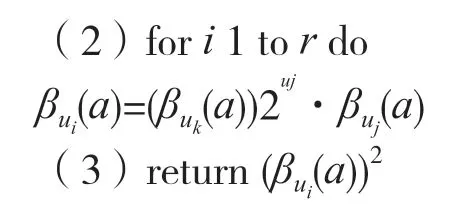
所以，当a∈GF(2233)时，可以得到加法链U=(1,2,3,6,7,14,28,29,58,116,232)。可以看到，求一次模逆运算仅需要10 次模乘和232 次模平方运算，具体的计算过程如表1 所示。由计算过程可知，每一步都具有相关性，只能串行执行。

表1 Itoh-Tsujii 模逆计算过程

在ECC算法中，模逆与乘法运算是分步进行的，因此可以将乘法器集成在模逆运算单元中，加上一个模幂运算单元组成乘/逆运算单元。其中，模幂运算可以利用一个计数器和一个模平方单元实现。具体的硬件结构如图5 所示。

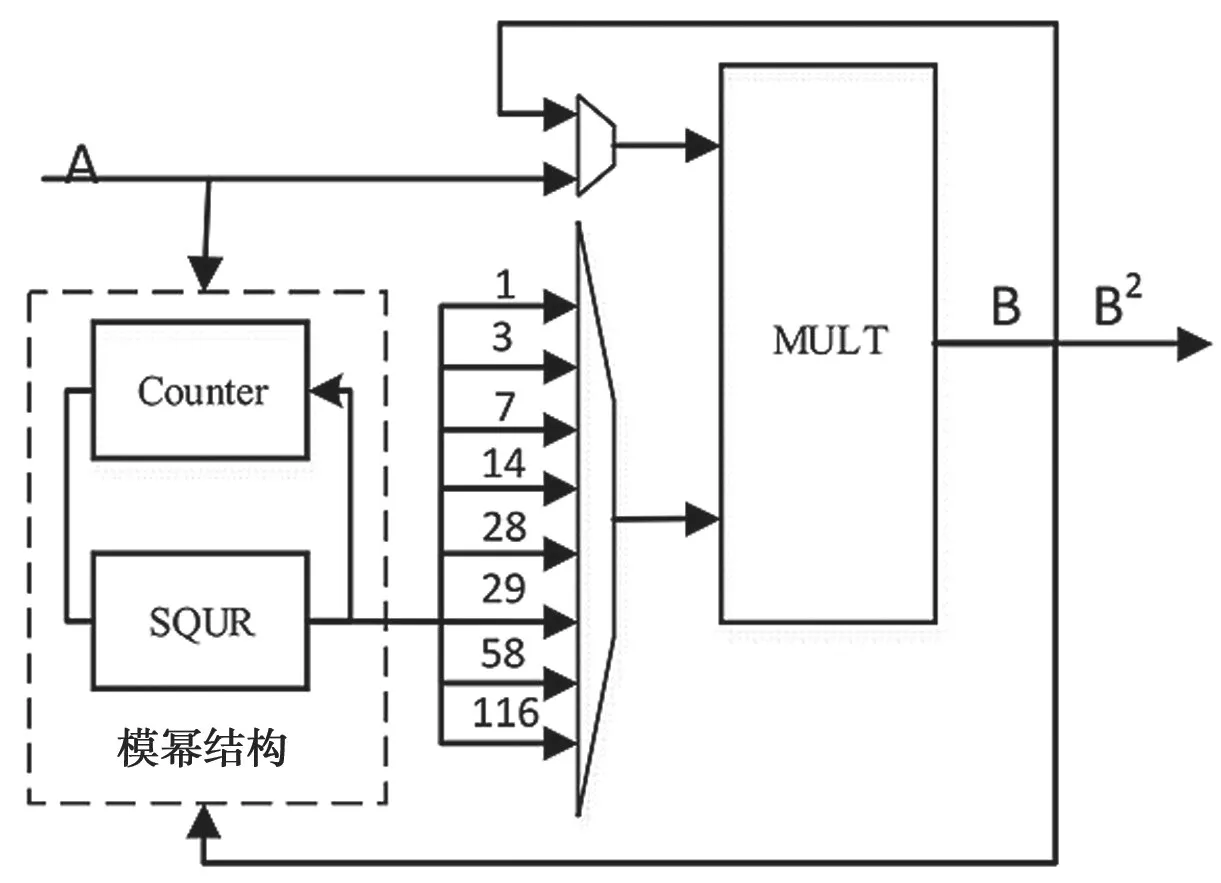
图5 GF(2233)域模乘/逆单元结构

3 点乘运算总体方案设计

3.1 点乘算法分析与设计

ECC 点乘算法包括模加、模平方、模乘和模逆运算，其中模逆运算的运算复杂度是其他运算的数十倍[10]。在仿射坐标下计算点乘需要多次模逆运算，而在投影坐标下只需要一次模逆运算。为避免进行多次模逆运算，本文采用投影坐标下的Montgomery点乘算法[11]。Montgomery 算法是现阶段最安全高效的点乘算法，相较于其他算法不需要进行预处理，且在计算过程中只用到点的横坐标，特别适合在硬件上实现。投影坐标下的Montgomery 算法包括初始化、主循环和坐标转换3 部分。

初始化部分主要实现对循环部分的输入数据初始化处理，输入投影坐标下点P(x0,y0)，输出投影坐标下点P1、P2，可以用两个模平方模块在1 个时钟周期内完成。P(x0,1)为点P 在射影坐标下的对应点，P2为P1的2 倍点，可以利用一个倍点运算在3 个时钟周期内实现。点加和倍点数据流分析，如图6所示。

主循环部分由m-1 次点加和倍点运算组成。由于两者之间没有数据依赖关系，可以同时计算。通过对循环部分的数据流进行分析，可以看出每次循环中共执行6 次模乘、5 次模平方及3 次模加运算。本文采用整体串行部分并行的结构，利用两个乘法器，将第i次循环中的点加和倍点运算（Montgomery算法中的①②（③④）步）划分为3 个阶段串行完成，每个阶段中的运算并行执行。

一次循环可以用2 个模乘模块、2 个模加模块和2 个模平方模块在3 个时钟周期内完成，因此整个主循环部分共需要3（m-1）个时钟周期。

坐标转换部分主要实现将投影坐标变换成仿射坐标，输入投影坐标下点P1、P2，输出仿射坐标下点Q(Qx,Qy)。主要计算过程为：

可见，它包括1 次模逆、10 次模乘、1 次模平方和7 次模加运算，可以用1 个乘法单元、1 个乘/逆单元、2 个加法单元和1 个平方单元在6+t个时钟周期内实现，其中t为一次模逆运算的时间。

3.2 总体电路结构设计

点乘运算3 个部分的结构可以共用，整体的硬件电路实现如图7 所示，共需要1 个模乘单元、1个模乘/逆单元、2 个模加单元和2 个模平方单元，共使用7 个寄存器X1、Z1、X2、Z2、T1、T2、R。其中，用来存储曲线的参数值x0、y0、b，寄存器X1、Z1、X2、Z2用来存储点乘算法中的坐标值，T1和T2寄存计算过程的中间值。

图7 点乘总体电路结构

4 实验结果分析

本文选用GF(2233)域上的Koblitz 曲线，y2+xy=x3+x2+1，对本文的点乘运算方案进行验证。以Artix7 器件中的XC7A100T 为硬件平台，利用Verilog 语言在FPGA 平台上进行结果仿真验证，并选用Modelsim 软件进行波形分析。图8 是本方案执行一次点乘运算的仿真结果。

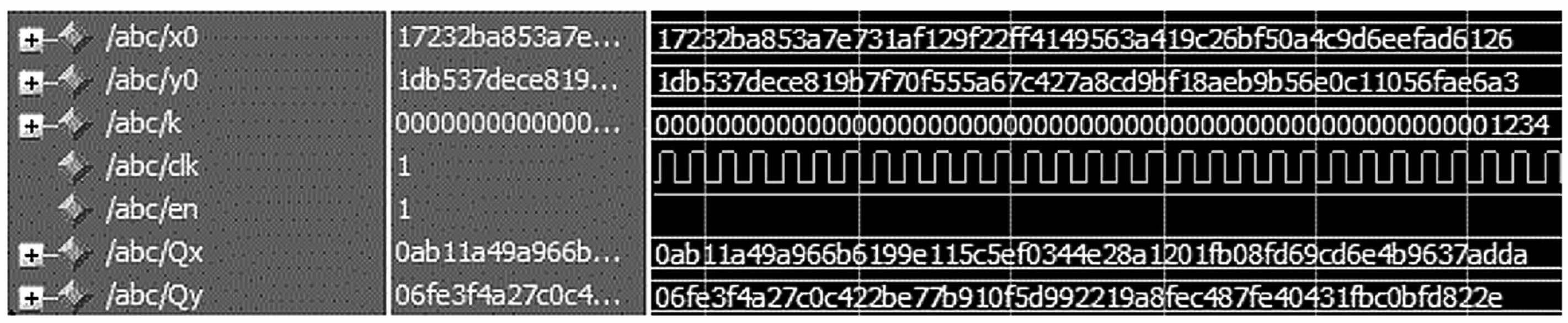
图8 仿真波形

根据本文设计的方案，在GF(2233)域内完成一次点乘运算共需要3+233×3+6+t个时钟周期，其中t为一次逆运算的时间。在FPGA 上的仿真结果及与其他方案的对比如表2 所示，算法执行过程中占用10 682 个Slices 资源，共用时1.644 4 ms。

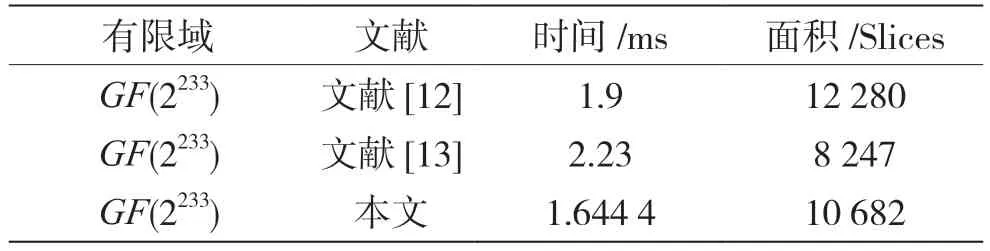
表2 测试结果及对比

通过与其他相关文献的对比可以看出，本文设计的点乘计算方案在占用面积和计算时间上都有所提升。

5 结语

本文通过对ECC 密码算法进行研究，针对不同运算层次的特点作了针对的优化改进，设计并实现了轻量化ECC 点乘计算方案。首，先通过对有限域的模运算单元进行研究，重点对模乘和模逆计算单元进行了改进；其次，根据Montgomery 点乘算法设计整体的计算流程，并以此为基础实现了有限域运算单元和整体点乘方案的电路结构设计。本文方案采用整体串行部分并行，经过在FPGA 平台上测试并与其他方案进行对比，达到了计算速度与占用面积的优化平衡，可以很好地适应于无线传感器网络等资源受限的场合。