一种基于单向HASH 函数的密钥矩阵加密方法*

于敬民，高媛媛

（陆军工程大学 通信工程学院，江苏 南京 210007）

0 引言

无线通信技术是人们生活中不可缺少的通信手段。但是，由于无线通信具有开放性和广播性，其信息的保密和安全一直是通信领域关注的问题。作为上层加密技术的补充，物理层加密技术是近年来提出的提高无线通信保密安全的有效方式。

物理层加密技术是利用无线信道的随机性、差异性和互易性等特性，结合信道编译码、调制解调和信号处理等技术，从物理层保护消息内容、调制方式等，为合法用户提供可靠通信的同时，防止窃听者获取有效信息的一种手段[1]。相比于传统的上层加密技术，物理层加密利用信道随机特性能够提供充足的密钥空间，保证信息的高度保密，同时具有低时延、低计算量的特点。在现今大数据、云计算兴起的信息时代，物理层加密方式已经成为一种有效的信息安全手段[2]。

人们在物理层加密技术上已经做了大量工作，各种加密方式层出不穷，如相位旋转加密[3]、符号模糊加密等，并根据量子互补原理、量子不可克隆原理和不可擦除原理研制了高度安全的量子加密技术，但是加密技术方面还存在加密算法困难、密钥空间匮乏等不足。

本文介绍的基于单向hash 函数的密钥矩阵加密方法密钥空间充足，加密算法简单，对信息的相位和幅值起到了良好的保护作用。由于单向hash 函数具有的抗碰撞性和不可逆性[4]，该方法可以较好地抵御明文密文攻击，提高信息的安全性。

本文首先介绍点对点的无线通信加密传输模型，其次分析密钥矩阵的生成过程以及加密和解密方式，最后从安全性和可靠性角度评估加密方案的性能。

1 密钥矩阵加密传输系统

本文针对最基本的无线传输模型即点对点的无线通信系统（如图1 所示），在对信息进行编码、调制后加入加密模块，从而实现对传输信息的加密（如图2 所示）。

图1 点对点无线传输模型

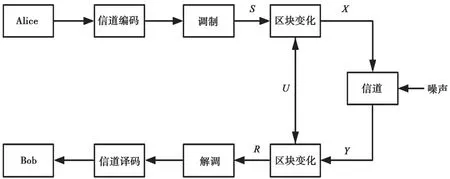
图2 点对点加密无线传输模型

首先发送端Alice 将所要传输的信息转变成二进制序列，经过信道编码和调制产生原始符号S=[s1,s2,…,sn]，调制方式可以是PSK 或者QAM 等。系统对产生的密钥序列进行区块变化，生成密钥矩阵U。将原始符号S和密钥矩阵U进行运算得到加密序列X=[x1,x2,…,xn]，将加密序列发送到合法信道中传输。接收端Bob 对接收到的信息Y=[y1,y2,…,yn]进行解密和去噪，得到接收符号R=[r1,r2,…,rn]。最后，对R进行解调和信道译码，得到原始的二进制序列信息。

1.1 密钥矩阵的生成

基于信道参数的密钥提取流程如图3 所示，主要包括信道特征测量、信道参数量化、一致性校验和密钥矩阵生成[5]。利用无线信道的随机性和不可预测性，理论上提取信道参数生成密钥，密钥具备良好的随机性。首先，Alice 和Bob 互相发送探测信号估计信道。根据信道的互易特性，在相干时间内双方的估计在某种程度上是相关的，因此理论上可以提取相同的密钥。

图3 基于信道参数的密钥提取流程

对获取的信道幅值|hB|采用如下方法进行量化。

首先，对|hB|进行归一化：

对|hB|N采用13 折线A 律编码，将|hB|N的范围变化到[-0.5,0.5]。按照13 折线A 律的编码规则，最终可以得到8 bit 的信道量化序列Q。

根据13 折线编码的量化规则，归一化后其量化精度为：

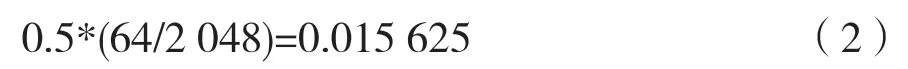
因此，归一化后的信道估计幅值在相差0.015 625 之内时，可生成相同的密钥矩阵。这一方面给予了接收端一定的估计空间，保证在存在误差的情况下依然可以正确解密，同时也给予了窃听端一定的破解余地。

根据信道互易性原则，理论上Alice 和Bob 生成的信道量化序列Q是相同的。但是，由于时延、噪声干扰、硬件环境等因素的影响，信道估计会产生一定的误差。为了解决上述问题，可以对信道量化序列进行一致性校验，如BBBSC 算法或者Cascade 协议，完成不一样的比特序列校正，从而生成一致的信道量化序列。最后，利用HMAC 算法和单向hash 函数，以信道量化序列为输入生成密钥矩阵。具体流程如图4 所示。

HMAC 算法是利用单向hash 函数，将两种输入信息结合，产生一种输出信息的算法[6]。本文中两种输入信息分别为信道量化序列和利用随机算法产生的随机序列。同时，定义两种8 bit 循环序列ipad 和opad，采用SHA-256 作为算法中的散列函数，函数分组长度为256 bit。由于最后生成的散列值会包含字母，因此这里定义由a～z 分别代表10～35。

密钥矩阵生成流程如下：

①将信道量化序列通过末尾补0 的方式扩充至64 bit。

②将信道量化序列与ipad 做异或运算，得到序列ipadkey。

③将随机序列与ipadkey 结合，组成新的序列。

④利用SHA-256 函数生成64 bit 散列序列num1。

⑤将信道量化序列与opad 做异或运算得到序列opadkey。

⑥将散列序列num1 与opadkey 结合，组成新的序列。

⑦再次利用SHA-256 函数生成64 bit 的散列序列num2。

⑧对散列序列num2 进行区块变化（即将64 位的散列序列转换为8×8 的矩阵，即n=8）。

⑨最后对H进行QR 分解：

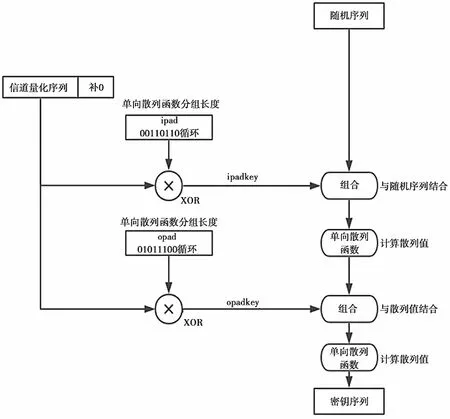
图4 密钥序列生成流程

其中，酉矩阵Q就是生成的密钥矩阵U：

合法接收者Bob 运用同样的算法即可生成密钥矩阵，然后对其共轭转置，便可得到解密矩阵UH。

本文采用随机序列作为其中一个输入信息，一方面增强了密钥矩阵的随机性，另一方面可以在相干时间内生成不同的密钥矩阵，增加了通信系统的安全性。利用SHA-256 函数可以生成容量较大的散列序列，提升了密钥矩阵的密钥空间。由于采用了HMAC 算法和单向hash 函数，即使信道估计存在略微差别，也会生成相差巨大的密钥矩阵，因此如果通信双发的密钥不完全一致，则无法实现解密，增加了通信系统的安全保密性能[7]。

1.2 加密过程

Alice 生成密钥矩阵后，将密钥矩阵U与符号序列S进行相乘运算，实现加密。

可以看出，加密运算使原有的符号序列S内所有的符号相互混叠产生了加密符号序列X。由于算法输入中包含随机序列，所以即使在相干时间内，不同的符号序列仍然可以采用不同的密钥矩阵加密。合法双方对随机序列生成的规律是已知的，因此很容易解密，但窃听端则很难破解密钥，从而提高了通信的保密性。

1.3 解密过程

Bob 接收到信号Y，通过解密矩阵UH对Y进行解密计算：

NB为信道的噪声，Bob 对R进行解调和判决就可以得到原始的二进制序列。仿真分析表明，密钥矩阵的引入并没有带来误码率的提升，因此无需考虑密钥矩阵对系统可靠性带来的影响，采用信道编码或者提高接收机的性能皆可改善噪声对误码率造成的影响。

2 仿真与分析

2.1 HMAC 算法和单向hash 函数性能分析

首先运用HMAC 算法保证信息的安全性。

①由于无线信道的独立性，不同空间位置的无线信道是唯一的，即合法信道和窃听信道的信道参数存在差异，因此窃听者无法通过计算得出与合法双方相同的密钥矩阵。

②由于算法利用随机序列，使算法具有瞬时性，在相干时间内可以对不同的信息实现不同的加密。

③在HMAC 算法的应用中，采用SHA-256 单向hash 函数具有高度的随机性，窃听者无法推测出下一个密钥。

另外，算法过程中运用单向hash 函数具备利于信息传输。

①对于给定的输入信息很容易计算散列值，保证了密钥生成的简单性。

②抗碰撞性，即随机找到两个消息M和M´，使得H(M)=H(M´)在计算上是不可行的，保证了密钥矩阵的唯一性。

③不可逆性，即无法通过H(M)反推输入信息M，保证即使密钥被窃听者窃取，窃听者也无法得到原始的信道量化序列。

根据上述特性，只要信道量化序列相同，便可以生成正确的解密矩阵。如图5 所示。

图5 信道估计误差与正确解密的概率关系

通过仿真当信道误差值小于0.015 时，存在47%～54%的概率可以正确解密。当误差值超过0.015 时，无法实现正确解密。从合法接收端来看，0.015 的容错空间可以使合法接收端在存在估计误差的情况下依然正确解密。从窃听端来看，由于窃听信道和合法信道存在差异，估计误差很难在0.015之内，因此可以保证系统的安全性。

2.2 加密星座图分析

如图6 和图7 所示，星座图可以清晰看出调制的方式。破解信息传输的调制方式也是窃听者窃听信息的重要环节，因此提高星座图的模糊程度可以大大加强对调制方式的保护[8]。

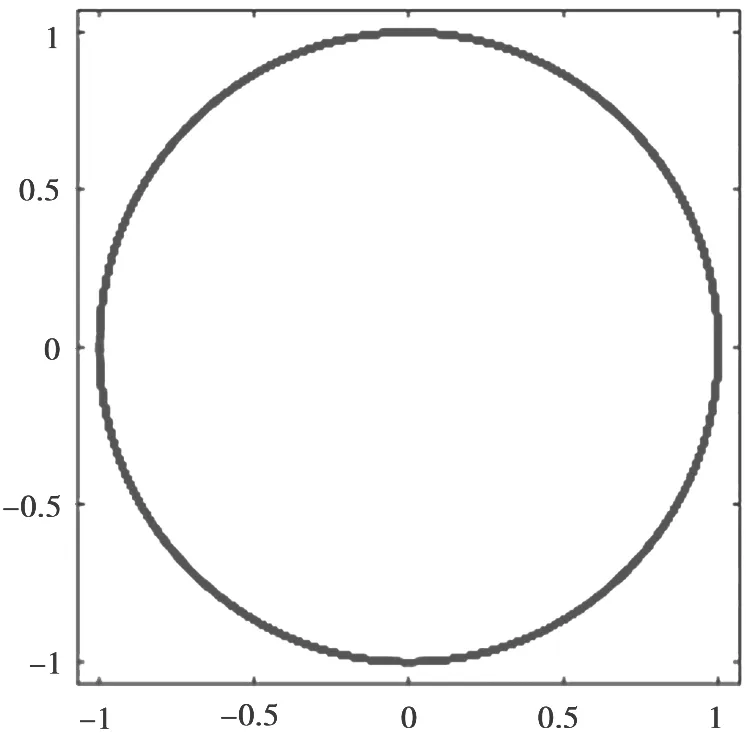
图6 4PSK 相位旋转加密星座

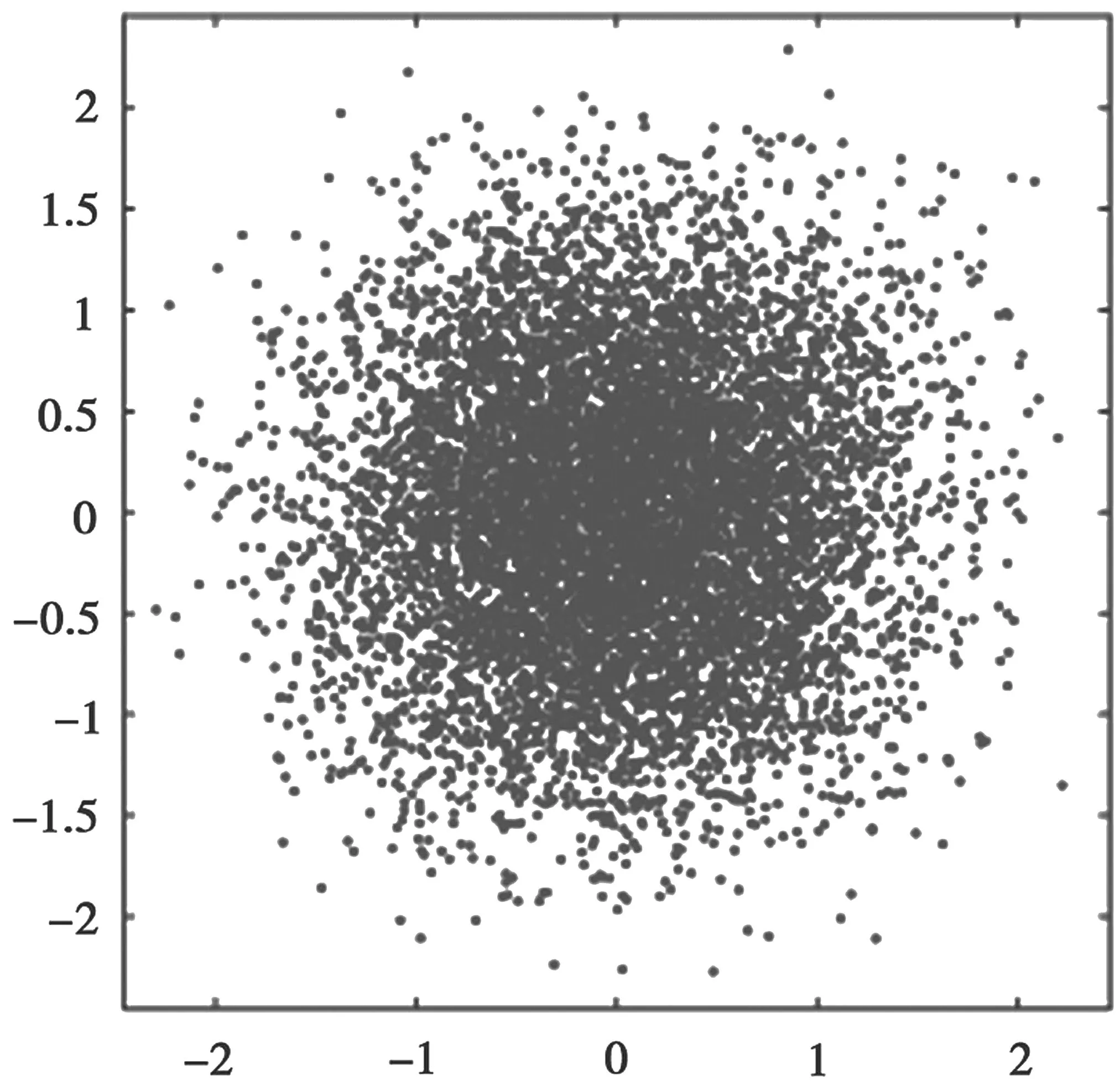
图7 4PSK 密钥矩阵加密星座

如图6 所示，4PSK 的相位旋转加密方法中，符号的映射点构成了一个圆，对信息调制的相位信息产生了良好的保护作用，但是幅度信息依然是暴露的，且星座图仍具有一定的规律性，系统的安全性还存在提升空间。图7 星座图的映射点混乱程度较高，对调制的相位和幅度信息都起到了良好的保护作用。

如图8 所示，采用16QAM 的调制方式，相比于4PSK 方式映射点的分布更加复杂，但是依然存在调制幅度信息暴露的问题。从图9 可以看出，无论是哪种调制方式，密钥矩阵加密的映射星座图都是高度混乱的，调制的相位和幅度信息都得到了保护，系统的安全性更高。

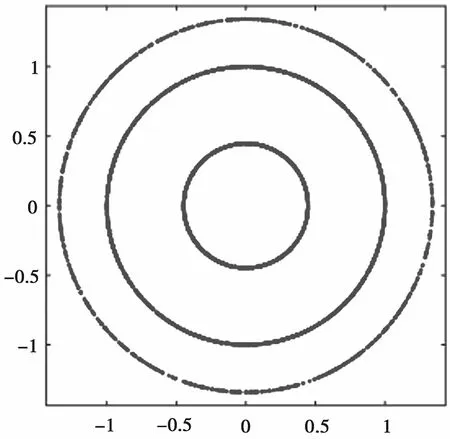
图8 16QAM 相位旋转加密星座

图9 16QAM 相位旋转加密星座

2.3 量化信息熵分析

为了从数据层面分析星座图的模糊程度，本文采用量化信息熵进行计算。假设加密信号x=a+j*b，量化信息熵的公式为[9]：

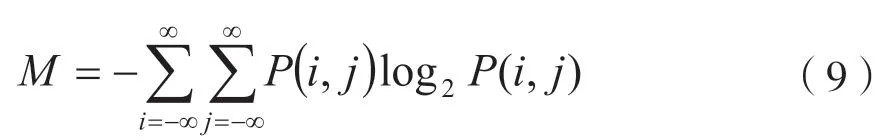
其中：

p(a,b)是a和b的联合概率密度。Δ 是量化精度，计算的量化信息熵越高，证明星座图越混乱，保密性越好。

本文以信噪比为10 dB、调制方式为QPSK 下的量化信息熵作为代表，仿真中设置数据长度分别为16 000 bit、80 000 bit 和160 000 bit，量化精度Δ=0.05，结果如图10 所示。

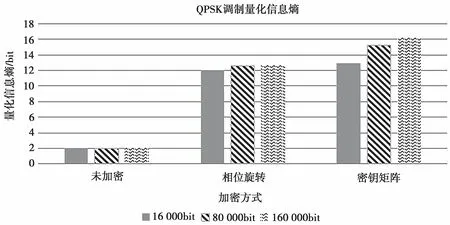
图10 量化信息熵对比

从图10 可以看出，信噪比为10 dB 的QPSK 调制下，当数据长度为16 000 bit 时，未加密的信息熵为2 bit，相位旋转加密的信息熵为12.09 bit，而密钥矩阵加密的信息熵为12.96 bit。可见，采用物理层加密技术对调制信息的量化信息熵有很大的提升作用，其中密钥矩阵加密方式量化信息熵更大。

当增加数据传输长度时，可以看出相位旋转加密的量化信息熵一直位于12 bit 左右，而密钥矩阵加密的量化信息熵达到了16 bit 左右。因此，数据长度越长，密钥矩阵加密的量化信息熵越高，星座图越模糊，系统的安全保密性越强。

2.4 仿真分析

本文在QPSK 的调制方式下对未加密的传输系统的合法接收端、密钥矩阵加密的合法接收端以及窃听者的误比特率进行计算。假设窃听者在完全不知道解密方式的情况下合法双发传输16 000 bit 的数据，结果如图11 所示。

图11 仿真对比

可以看出，在没有破解密钥的情况下，窃听者的误比特率非常高，达到了0.5 左右。另外，采用密钥矩阵加密方案并没有牺牲发送功率来换取通信的安全性，理论上根据无线信道的互易性并进行严格的一致性校验，合法双方能够生成一致的密钥矩阵。所以，与未加密系统相比，密钥矩阵加密方案没有造成合法接收者误比特率的上升，没有降低系统的可靠性。

3 结语

本文提出的基于单向hash 函数，利用HMAC算法的加密方案，对信息符号的幅值和相位起到了有效的保护作用，发端星座图呈现良好的随机性和高度的模糊程度，量化信息熵能够超过相位旋转加密方式，并随着传输数据长度的增加，相差更大。从误比特率角度来看，理论上加密方式并不会带来误码率的提升，同时在没有破解密钥的情况下窃听端误比特率高达0.5 左右，在保证安全性的同时没有降低通信系统的可靠性。另外，根据单向hash 函数和HMAC 算法的抗碰撞性和不可逆性，从理论上基于hash 函数密钥矩阵加密方案可以抵御窃听端对密钥的破解。