偏振纠缠双光子态的量子测距方案*

姚禹迪

（西南交通大学量子光电实验室，四川 成都 610031）

0 引言

量子纠缠态是在量子力学理论研究中非常重要的课题，广泛存在于多自由度体系和量子力学多粒子体系，自身具备很强的特殊性。通过对量子系统的不断研究探索发现，量子纠缠最具有代表性的特征是，人们对一个系统中的某个具体的子系统进行测量的结果无法与其他子系统的参数或是参量独立分开，也就是在测量其中某个具体的子系统时，其余的子系统对应的测量参数也会被逐步确定。为了便于理解，以纠缠双光子态为观察对象。不管两个光子距离相差多远，这两个光子相互间存在着特别的关联特性。特别是当针对于其中某个具体的光子实现测量时，与其纠缠的其他的具体光子状态通常会产生相应的改变。1935 年，著名学者Podolsky、Einstein 以及Rosen 基于大量研究和分析，编写了重要的文章成果，成为后来学者的研究理论依据，对于纠缠态研究的理论基础，被称作EPR 佯谬[1]。同年年初，著名学者Schrodinger 在搜集大量数据和资料的基础上编写了文献[2]，其中针对性地列举了两粒子体系对应的波函数的本质是非定域性纠缠态。在Schrodinger 的文章里涉及到的猫态，本质上看属于纠缠态。纠缠态的出现，使得人们开始广泛研究正统量子力学，促使同纠缠态有关的实验和理论快速发展。

截至目前，针对我国实验的具体情况来看，我们拥有很多能够完成纠缠态制备的方法，如基于非线性晶体（如BBO 晶体）的非线性效应进行参量下转换过程的制备纠缠态。采用该方法的有利之处在于其便于操作，且产生纠缠光子对的产率很高。1999 年，Kwiat[3]等人通过改进叠加两片I 型BBO晶体为基础，进一步提高了纠缠光子的产率。

量子力学涉及测不准原理，而该原理阐述了海森堡极限的理念，能够确定所有的测量精度对应的极限最大值，而使用比较传统的测量技术是不可能达到的，只可以完成测量工作。当工作人员在测量技术中加入量子纠缠理论时，基于特定状况察觉到现测量精度是能够突破传统测量极限（散粒噪声）的。现在社会有关量子理论正处于持续进步和发展阶段，因此对于量子测距技术的分析和研究至关重要。

1 基本原理

光场中，分析其中光的相干性与统计性质，通常使用关联函数来实现。基于经典光学的层面来看，通常采用一阶关联函数。但是，微观领域也会涉及量子关联的研究，需要引起注意[4-6]。

通常阐述的HBT 测量能够将其称作二阶相干测量，如图1 所示。1956 年，著名学者Richard Q.Twiss 以及Robert HanburyBrown 在Michelson 星体干涉仪的基础上开发了初期的强度干涉仪，能够测量光场强度涨落对应的有关函数[7-8]。

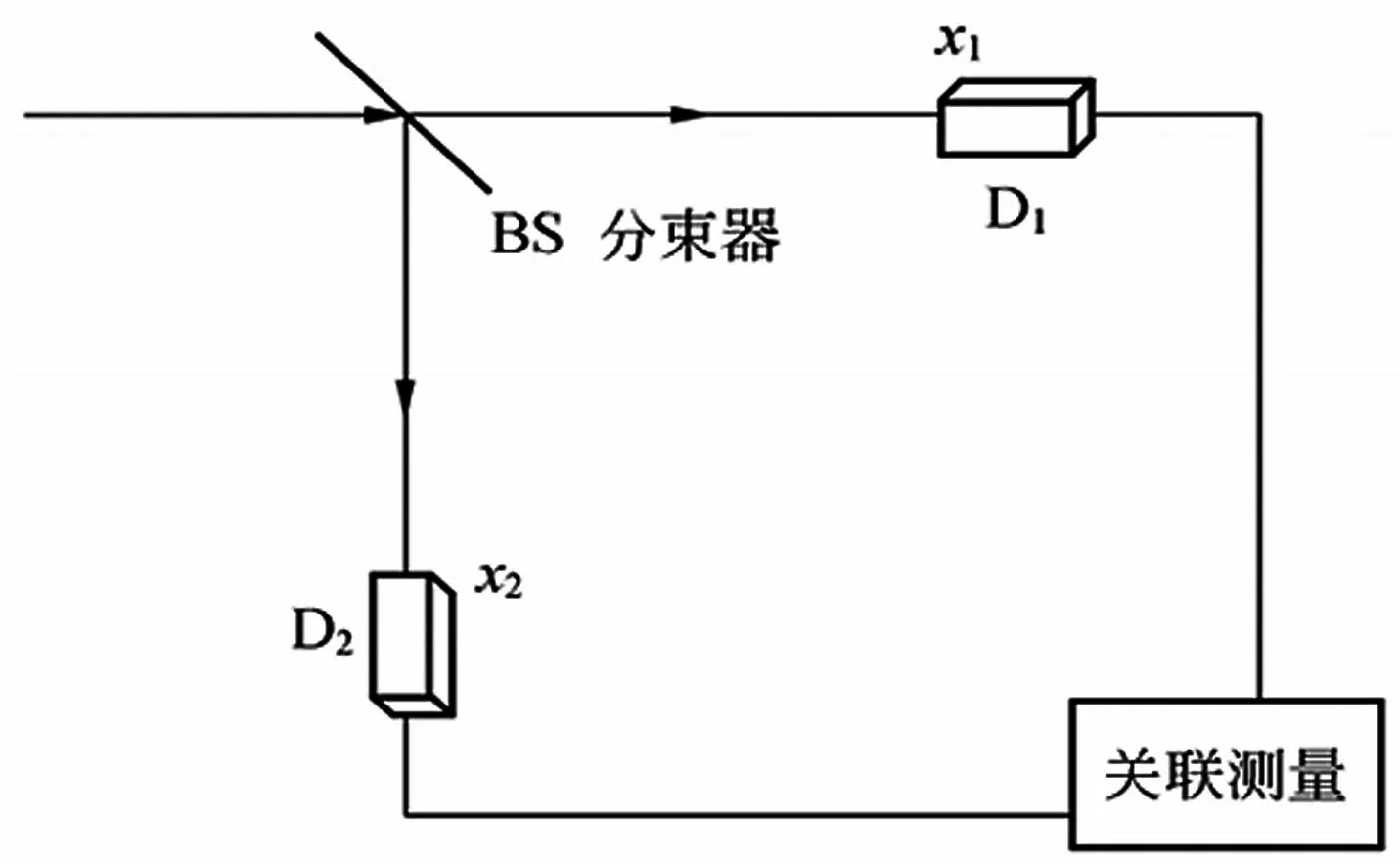
图1 HBT 符合测量实验

所有的光信号都是基于光源发出的，通过干涉后到达单光子检测器，位于时间(0,t)中，能够检测光子概率：

这里检测效率用k表示。站在多路关联实验的层面上看，存在n路光信号通过多路关联干涉后，随后会来到n个单光子检测器，其检测到光子的概率为：

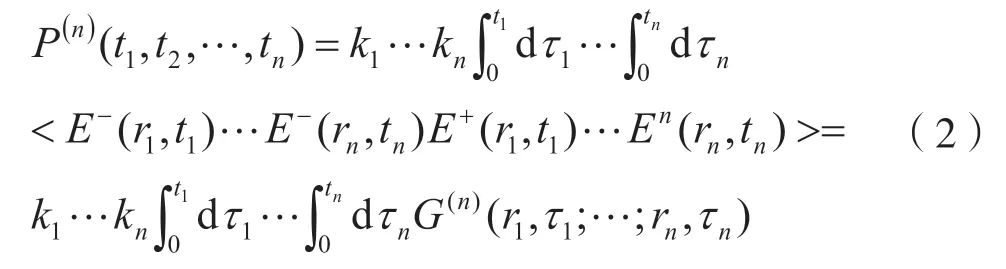
其中n阶关联函数为：

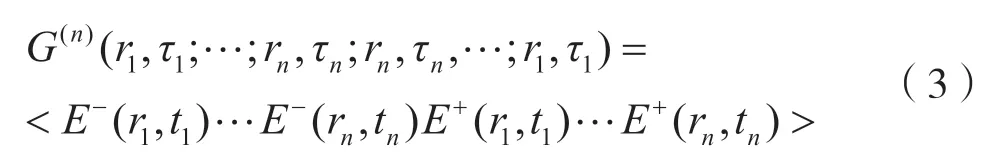
归一化后的n阶关联函数为：

通常来讲，以n阶关联函数为观察对象，它并不能够具体划分成n个一阶关联函数互相乘积的方式，即：

特别的，当n=2 时，可以得到光场的二阶关联函数：

归一化的二阶关联函数为：

在加入纠缠光子对时，对处在两个不同时空点(r1,t1)和(r2,t2)（r1和r2接近为零），τ=t1-t2时的光场的二阶关联特性为：

当τ=0 时，有G(2)(τ)=G(2)max。

当t1=t2即τ=0|τ0时，此时二阶关联函数的最大峰值会在τ0出现。

当t1≠t2时，二阶关联函数的最大峰值会出现在τ=t1-t2处。

2 实验系统与结果分析

偏振纠缠双光子包含两路光束——信号光路与闲置光路。基于纠缠光成对出现的现象，当激光光子经过II 类BBO 晶体发生参量下转换产生相应的纠缠光子信号、信号光子与闲置光子。两路光子经过不同的空间光路传输时，纠缠的主要表现是以两个光子为观察对象，在时间上具备了纠缠关联特性。

通过图2 的内容可以发现，其中的泵浦光主要是基于半导体激光器为主体而产生的持续激光，且该激光对应的中心波长为405 nm，功率约为90 mW，激光的偏振方向为垂直偏振。之后经过滤光片滤除噪音，由此获得纯净激光。随后借助两片反射镜完成光路的调节工作，同时使其在水平状态上保持，调节偏振片来固定激光的偏振方向，经过透镜后汇聚垂直入射到BBO 晶体。当来到BBO 晶体后会出现自发参量基础的转换过程，这种情况下光路主要能够划分成3 路——信号光、闲置光和未发生转换的泵浦光，并用光学垃圾桶收集残留的泵浦光。随后信号光照射到目标（反射镜），反射回的信号光经过光耦合器进入光纤；而闲置光进入光耦合器到达光纤中，再经过光纤延迟器改变光路延迟。

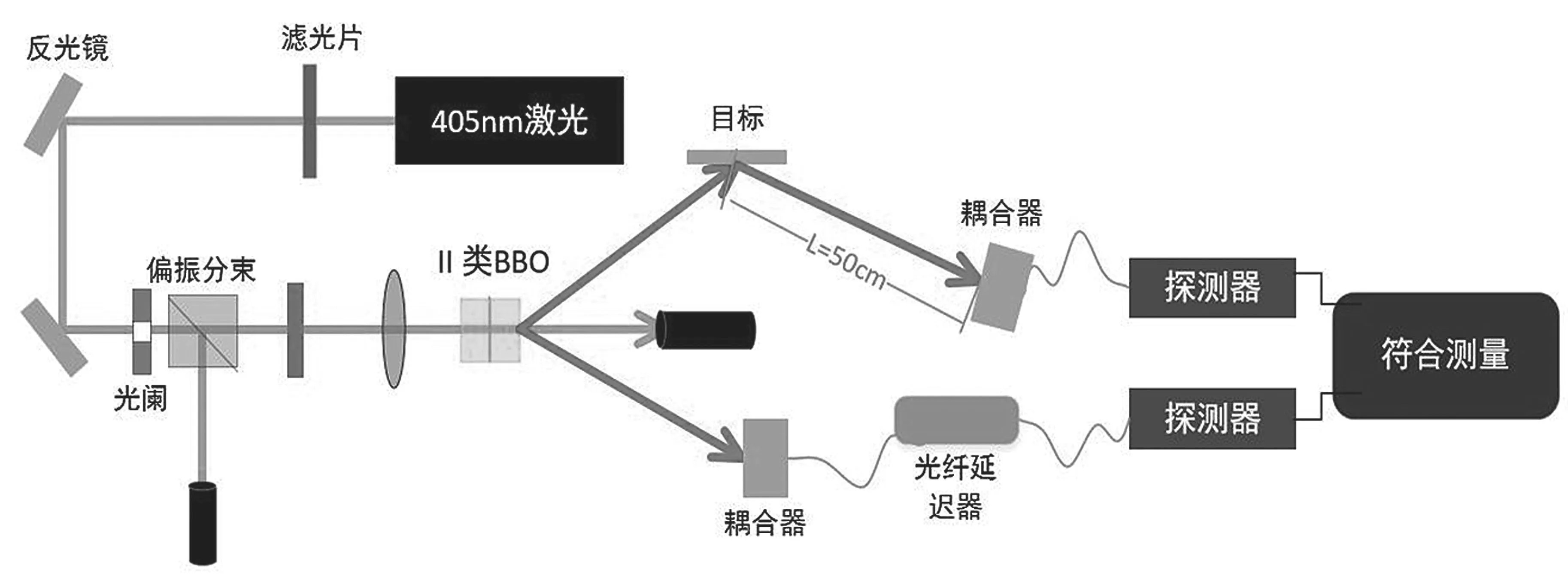
图2 实验架构

通过调解闲置路上的光纤延迟器，使得符合测量结果在0 延时处达到最大，从而根据延迟器的延迟时间τ得到目标的距离信息。

假设信号光和闲置光各自的传播时间分别为t1和t2，光的传播速度为c，那么光程差L即光源到待测目标的距离：

处于实验室现具有的条件中完成缠测距实验，首先应该将耦合端同参考光纤相连接，完成相应的数据采集工作，由此将其标记为首次测量。其次，在信号光路放入距接收距离50 cm（待测距离）的反射目标，光纤延迟器调为0 延迟进行第二次数据采集，记为第二次实验。最后，调节光纤延迟器的延迟，符合数据结果在0 延迟时刻再次达到最大。测量结果依次如图3、图4 和图5 所示。

经过曲线拟合，可以得到第一次测量时的中心峰值处的延迟时间为τ1=21ps；第二次测量时的中心峰值处的延迟时间为τ2=1 623ps；在第三次测量时，调节光纤延迟器使得的中心峰值处再次达到最大处，此时的符合曲线上的延迟时间为τ3=16ps，而此时在光纤延迟器上的延迟读数为τ=1 665ps。

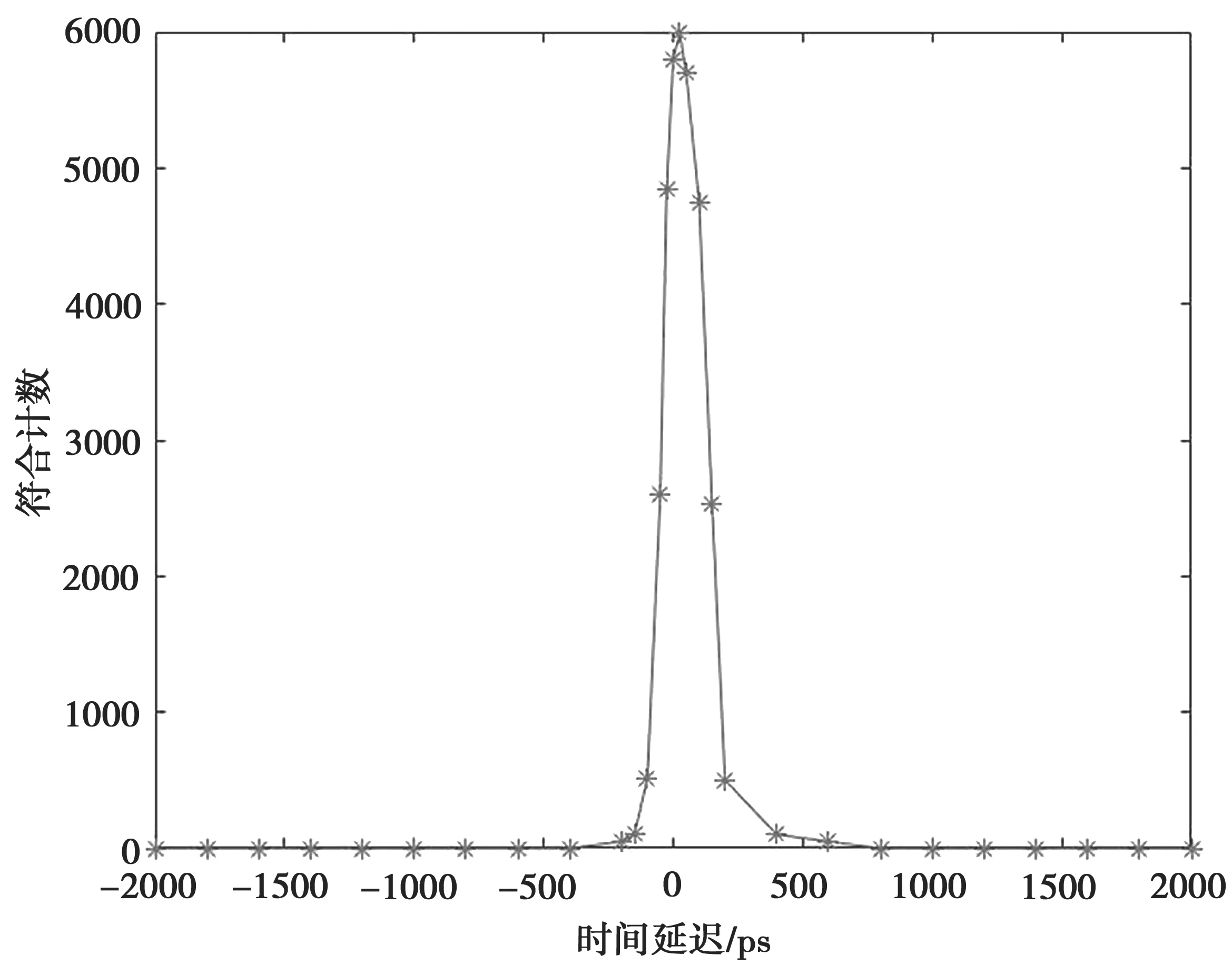
图3 第一次测量结果

根据上述提到的式（9），计算距离：

可以看出，在使用高精度的光纤延迟器调节延迟后，根据延迟器读取数据得到的测量距离结果接近实际的待测距离。可见，提出的利用光纤延迟器结合二阶关联测量原理的测距方案，在实验上是可行的。

图4 第二次测量结果

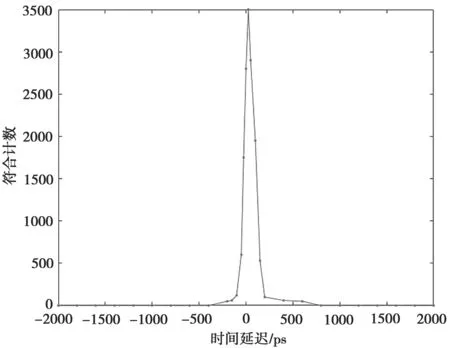
图5 第三次测量结果

3 结语

本文对于量子纠缠测距实验进行了有关讨论。基于纠缠光场的二阶关联理论，提出了利用光纤延迟器调节延迟时间的一种测距方案。在这个基础上搭建测距实验环境，在实验室现有条件下测量50 cm的短距离目标，并得到了初步可行的结果，开展实验验证，进一步观测各个参数对测量精度、量程等系统指标的影响。初步的理论分析和实验结果表明，提出的方案具有可行性，可为未来量子测距实验提供参考。