一种混叠采样条件下的自适应LMS 方法*

刘 宁

（中国西南电子技术研究所，四川 成都 610036）

0 引言

过去20 年，无线通信在全世界得到了快速迅猛发展，其中自适应信号处理广泛应用于无线通信的中射频领域，主要包含均衡、功放预失真、回波对消以及通道均衡等关键技术。随着调制技术的不断革新，通信信号的带宽不断加宽，对采样率提出了愈高的要求，现有数模转换器件已经不能满足信号带宽的需求。如何在采样率不足的条件下完成自适应的学习过程，成为亟待解决的技术难点。

本文从基本采样理论着手，分析采样混叠后信号的特点，算法设计中合理设置中频频率与采样率的关系，推导出了一种在混叠信号中进行自适应信号误差计算的方法，通过实验确认了其可靠性和有效性。

1 采样混叠

图1 为将连续时间模拟信号转换到数字信号的A/D 转换器原理框图[1]，采样周期为T。A/D 转换器的等效处理过程如图2 所示。

图1 采样A/D 转换示意

图2 等效采样过程

通过傅里叶变换可推导出xs(t)的频域表示：

考虑xc(t)为一种带限信号，其最高频率成分为ΩN，其频谱如图3 所示。

图3 原始连续时间信号频谱

显然，当Ωs-ΩN＞ΩN时，Xs(jΩ)频谱如图4 所示，原始信号可从采样后信号中完全重构，信号未产生失真。

当不满足奈奎斯特采样定律时，采样后信号会产生如图5 所示的混叠现象，使得无法从采样后信号重构出采样原始信号，则不能利用混叠后的采样信号进行有效正确的相关数字处理[2-3]。

图4 理想采样信号频谱

图5 混叠采样信号频谱

2 算法设计

2.1 特定采样率与中频频率下的采样信号

若信号f(t)=A(t)cos(f0t+φt)，带宽为B，在奈奎斯特采样定律的保证下进行采样，可以得到其可重构的无失真基带复信号[4-5]：

考虑如图6 所示的中频采样过程，其中f(t)是待采样中频模拟信号，中频频率为f0，采样率为fs。对f(t)=A(t)cos(f0t+φt)直接的等效数学表示如下：

图6 混叠采样过程

不妨设置采样率fs与中频频率f0的关系为，则中频直接采样后信号可推导为：

将式（5）展开，可得：

不妨再设置采样率fs与中频频率f0的关系为，则中频直接采样后信号可推导为：

将式（7）展开，可得：

比较式（6）和式（8）可见，通过设置不同的采样率fs与中频频率f0的倍数关系，可以得到不同混叠程度的采样信号。正如前面推导，如果合理设置，那么会得到式（8）的采样结果。一般实现中去掉符号的影响，则式（8）可转换为：

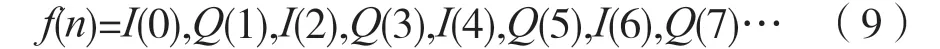
满足奈奎斯特条件下，得到的基带信号应为：

（1）式（9）采样结果得到过程中没有限制采样率fs和带宽B的关系，即在任何带宽B的条件下，不改变式（9）的结果；

（2）式（10）采样结果得到过程限制了采样率fs和带宽B的关系，即必须满足奈奎斯特采样定律。

（3）虽然式（9）得到的采样结果产生了混叠，但其采样信号刚好是式（10）理想采样基带信号的正交信号和同相信号的抽样合并。

显然，在基于图6 的采样结构下，设置中频频率与采样率的关系为，这样采样过程可以完全不满足奈奎斯特采样条件的要求，不限制采样率fs和带宽B的关系，得到的混叠采样结果恰好是理想采样基带正交信号和同相信号的抽样合并。

2.2 采样混叠条件下的自适应LMS 算法

对于如图7 所示的维纳滤波过程，横向滤波器的输入和期望响应都为广义平稳随机过程，且已知其二阶统计特性，根据最小均方误差准则求得最优滤波器参数。实现中一般采用迭代LMS 算法进行求解。

图7 维纳滤波过程

根据维纳滤波和LMS 算法理论，对其横向滤波器系数权向量的更新数学表示为：

实际工程中，为了避免白噪声的影响，一般对误差信号求平均后进行迭代运算，则e(n)可表示为：

结合式（13）和式（9）可以在混叠采样条件下解算出自适应LMS 算法的误差信号e(n)，从而完成迭代运算，完成权向量的收敛回归计算。这种方法只需要设置中频频率与采样率的关系为，不限制采样率fs和带宽B的关系，特别是在宽带信号应用中，不再对A/D 的采样率提出高的要求。值得注意的是，由于混叠采样在同样时间段内获取的基带信号不是完整的同相与正交分量，所以可用于计算的误差数据个数少于理想采样。例如，采样的条件下，混叠采样采用的误差数据是理想采样的一半，故而混叠采样的收敛时间是理想采样的2 倍。

3 仿真及实验结果

考虑如图7 所示的维纳滤波过程，期望响应为观测信号经过一个2 阶横向滤波器滤波后的输出，其系数w1=1，w2=3，分别利用理想采样后的基带信号LMS 算法和本文提出的混叠采样条件下的LMS算法进行仿真分析，仿真使用中频频率与采样率的关系为。

理想采样及混叠采样权向量收敛曲线分别如图8和图9 所示，两者权向量均收敛到目标值w1=1，w2=3。

图8 理想采样权向量收敛曲线

图9 混叠采样权向量收敛曲线

图10、图11 分别表征了理想采样及混叠采样误差收敛曲线。

图10 理想采样误差收敛曲线

图11 混叠采样误差收敛曲线

可见，混叠采样收敛于第2 000 次迭代左右，而理想采样收敛于第1 000 此迭代左右，收敛时间混叠采样是理想采样的2 倍，与理论推导相符。如表1 所示，两者具备相同的收敛性能，收敛误差均收敛于同样的稳态误差即4.19e-13。

表1 收敛稳态误差

4 结语

本文提出的一种采样混叠条件下的自适应LMS算法，合理配置中频频率与采样率的关系，从采样已经混叠的信号中恢复出可用于自适应计算误差计算的基带信号，以收敛时间为代价，利用其进行误差计算更新迭代，并收敛于与理想采样同样的稳态误差，可广泛应用于均衡、数字预失真、对消以及通道校准等广泛的自适应信号处理的应用。同时，采样率的配置与信号带宽无关，极大降低了对大带宽、高速率A/D 转换器的要求，使得其在宽带信号处理中的应用具备巨大的潜力。在后续研究中，可详细分析对不同中频频率与采样率配置，推导出不同配置下的基带信号，从而优选出中频频率与采样率的配置关系。