激发正交相干态的构建及其量子特性

吴亚女

激发正交相干态的构建及其量子特性

吴亚女

(漳州工业学校, 福建 漳州, 363000)

利用产生算符作用在正交相干态上构造新的量子态的方法, 构造了激发正交相干态。采用数值计算方法, 通过对光场的两个正交分量涨落、二阶关联函数、Mandel Q参量的计算, 讨论了该量子态的统计性质, 并研究了产生算符作用次数和相干态平均光子数对其量子特性的影响。结果表明: 激发正交相干态不呈现压缩效应, 但呈现出反聚束效应和亚泊松分布性质, 并且随平均光子数增大它的反聚束效应、亚泊松分布性质均减弱。另外, 算符作用次数对其量子特性有重大影响, 选择二次作用对增强态的反聚束效应和亚泊松分布性质有利。

量子光学; 算符重复作用; 激发正交相干态; 量子特性

光场量子态的构建, 量子特性的研究, 及其在开放系统中量子特性的保持等, 长期以来一直是量子光学领域研究的重要课题。在量子态构建方面, 常用的方法有2种: 一是利用量子力学态叠加原理, 如薛定谔猫态等[1–2]; 另一种是利用算符作用在参考态上构建新的量子态。

在算符作用方法方面, Agarwal等[3]最早引入了利用光子产生算符构造激发相干态的方案, Agarwal等[4]讨论了单光子减压缩真空态的非经典性质。随着研究的深入, 研究者们在湮没算符和产生算符单独作用的研究基础上, 将算符作用推广到算符叠加作用, 产生算符和湮没算符先后作用, 以及算符累次作用等情况[5–13]。如: Wu等[5]通过一模光子增加到双模压缩真空态上来构建新的量子态, 并讨论了它的统计性质; Wang等[6]研究了多光子减双模压缩相干态的非经典性质; Xu等[7]提出了湮没算符和产生算符先后多次作用在压缩真空态上, 构建新的量子态方案, 并考察了它的量子特性。实验上, Zavatta等[14]实现了利用Bose产生算符作用产生单光子激发相干态。近年来, 研究者们还提出了构建参考态的正交态的新思想, 并在实验上提出制备正交态的方案[15–17]。受前面研究的启发, 本文将产生算符作用在正交相干态上构建了激发正交相干态, 并讨论其统计性质, 如压缩效应、反聚束效应、亚泊松分布等。

1 激发正交相干态的构建

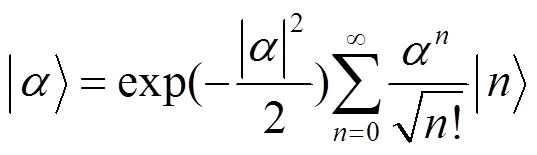
式中(,)为归一化常数。利用积分公式[19]

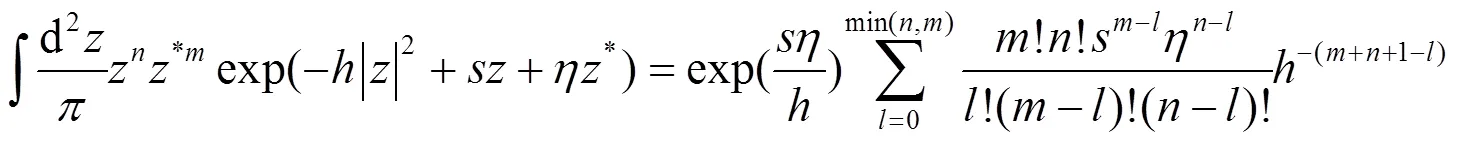
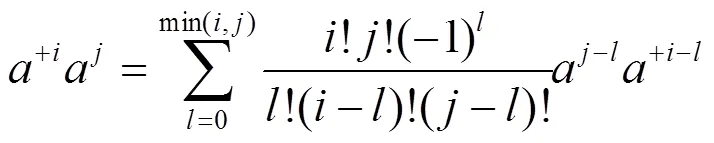
为了计算简单起见, 以下我们仅考虑= 1的情况, 这时

利用式(3), 具体计算得出

,

2 压缩效应

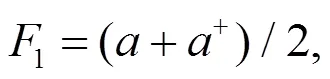
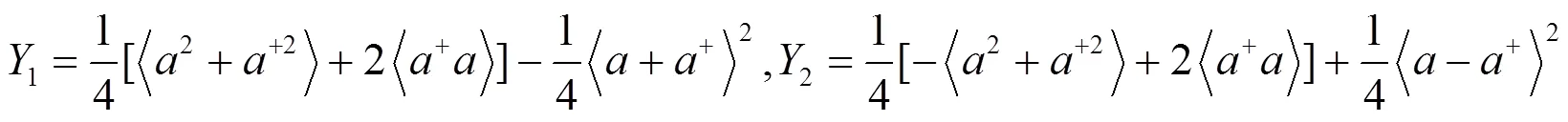
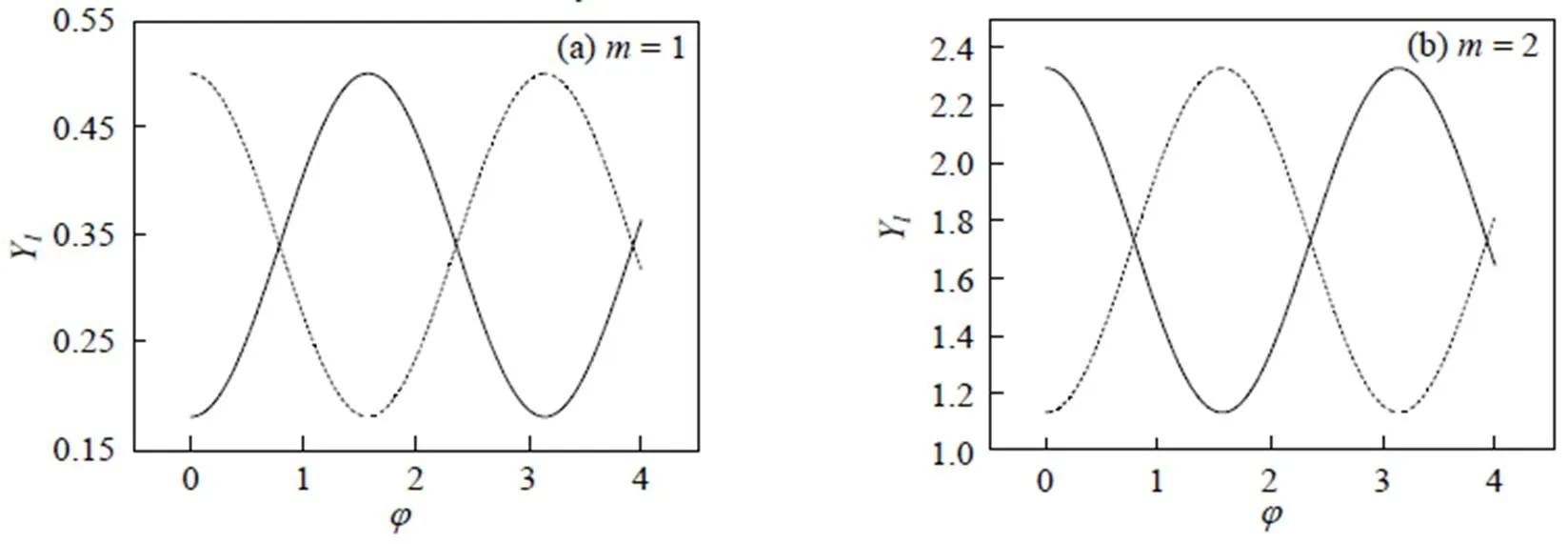
3 反聚束效应

光场的反聚束效应可用二阶关联函数来描述, 定义为[19]

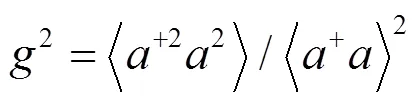
定义=2-1, 若< 0, 则称光场呈现出反聚束效应。

4 光场的统计性质

Mandel Q参量描述了光场的统计分布性质, 定义为[19]

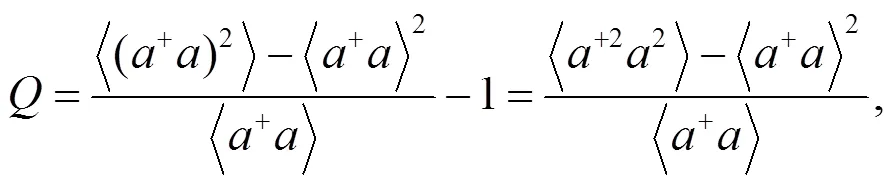
= 0表示其统计分布性质为泊松分布, 而> 0 (< 0)表示其统计分布为超泊松分布(亚泊松分布)。

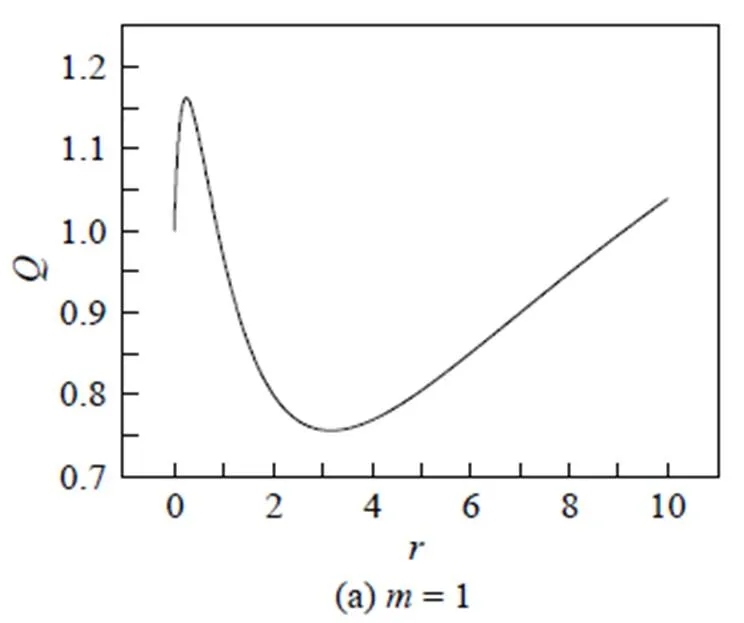
将式(4)的结果代入式(7), 可对Mandel Q参量随平均光子数的演化进行数值计算。计算结果如图3所示。由图3可知: 图3(a), 激发数= 1, 这时> 0, 表明EOCS态呈现出超泊松分布; 图3(b)和3(c), 激发数分别等于2和3, 在小于一定值的区域内< 0, 这时EOCS态表现出亚泊松分布性质。激发数= 2的曲线负值区域要比= 3的曲线负值区域大, 说明其亚泊松分布性质要比= 3的强。比较图3(a)、(b)、(c), 发现激发数对EOCS态的统计分布性质也有重要影响。计算结果表明, 选择激发数= 2对增强EOCS态的亚泊松分布性质也有利。另一方面, 其亚泊松分布性质随相干态平均光子数增大而减弱, 相干态平均光子数大于一定值后, 亚泊松分布性质消失。

5 结论

[1] 闫红梅, 李淑静, 何亚亚, 等. 相位抖动对“光学薛定谔”猫态制备的影响[J]. 量子光学学报, 2019, 25(1): 6–14.

[2] 李鹏茂, 萨楚尔夫, 苏少龙, 等. 薛定谔猫态光场与二能级原子相互作用系统的量子特性[J]. 原子与分子物理学报, 2015, 32(2): 275–280.

[3] Agarwal G S, Tara K. Nonclassical properties of states generated by the excitations on a coherent state [J]. Physical Review A, 1991, 43(1): 492–497.

[4] Biswas A, Agarwal G S. Nonclassicality and decoherent of photon-subtracted squeezed states [J]. Physical Review A, 2007, 75: 032104.

[5] Wu W F, Fan H Y. Single-mode photon-addition for the two-mode squeezed state and its statistical properties [J]. International Journal Theoretical Physics, 2017, 56(8): 2 651–2 658.

[6] Wang S, Yuan H C, Xu X F. Photon statistical properties of multiple-photon-subtracted two-mode squeezed coherent states [J]. Optics Communications, 2013, 298-299: 154–160.

[7] Xu X X, Yuan H C, Zhou L. Nonclassicality generated by repeatedly operating photon annihilation-then-creation and creation-then-annihilation on squeezed vacuum [J]. Optics Communications, 2015, 325: 133–139.

[8] Gu Yu-Wan, Shi Guo-Dong, Sun Yu-Qiang, Wang Shuai. Nonclassical propeities of multiple-photon-added two-mode squeezed coherent states [J]. Int J Theor Phys, 2014, 53: 1 784–1 796.

[9] Zhou J, Fan H Y, Song J. Photon-subtracted two-mode squeezed thermal state and its photon-number distribution [J]. International Journal Theoretical Physics, 2012, 51(5): 1 591–1 599.

[10] Lee S Y, Nha H. Quantum state engineering by a coherent superposition of photon-subtraction and addition [J]. Phys. Rev. A, 2010, 82(5): 053812.

[11] Hu L Y, Xu X X, Wang Z S, et al. Photon-subtracted squeezed thermal state: nonclassicality and decoherence [J]. Phys. Rev. A, 2010, 82: 043828.

[12] Zhou J, Song J, Yuan H, et al. The statistical properties of a new type of photon-subtracted squeezed coherence state [J]. Chinese. Physics Letters, 2012, 29(5): 050301.

[13] 兰海江, 庞华锋, 韦联福. 多光子激发相干态的Wigner函数[J]. 物理学报, 2009, 58(12): 8 281–8 288.

[14] Zavatta A, Parigi V, Kim M S, Jeong H, Bellini M. Experimental demonstration of the bosonic commutation relation via superpositions of quantum operations on thermal light fields [J]. Physical Review Letters, 2009, 103(14): 140406.

[15] Vanner M R, Aspelmeyer M, Kim M S. Quantum state orthogonalization and a toolset for quantum optomechanical phonon control [J]. Physical Review Letters, 2013, 110: 010504.

[16] Jezek M, Micuda M, Straka I, et al. Orthogonalization of partly unknown quantum states [J]. Physical Review A, 2014, 89: 042316.

[17] Coelho A S, Costanzo L S, Zavatta A, et al. Universal continuous-variable state orthogonalizer and qubit generator [J]. Physical Review Letters, 2016, 116: 110501.

[18] Yuan H C, Xu X X, Cai J W. Induced states from coherent state via photon-addition operation [J]. International Journal of Theoretical Physics, 2019, 53(6): 1 908–1 926.

[19] Ren G, Ma J G, Du J M, et al. Non-classical properties of photon-added compass state [J]. International Journal of Theoretical Physics, 2014, 53(3): 856–869.

[20] 范洪义, 楼森岳, 潘孝胤, 等. 涉及双变量多形式的二项式定理及其在量子光学中的应用[J]. 物理学报, 2014, 63: 110304.

The construction of the excited orthogonal coherent state and its quantum properties

Wu Ya’nv

(Zhangzhou Industrial School, Zhangzhou 363000, China)

Excited orthogonal coherent state (EOCS) is constructed by repeat operation of photon creation operator on the orthogonal coherent state. The squeezing, anti-bunching effect and sub-poissonian statistical property of EOCS are studied by using numerical calculation method. The influences of the repeat operation number of creation operator and the average number of photon in the coherent state on its quantum properties are discussed. Numerical results show that EOCS does not exhibit squeezing effect, but it displays the anti bunching effect and the sub-poissonian statistical property; in addition, its anti-bunching effect and sub-poissonian statistical property are weakened with increase of the average number of photon in the coherent state. On the other hand, the repeat operation number of creation operator has a significant impact on its quantum properties, and the two times operation of creation operator is benefit to strengthen its quantum properties.

quantum optics; the repeat operation of creation operator, excited orthogonal coherent state; quantum property

O 431.2

A

1672–6146(2020)03–0014–05

10.3969/j.issn.1672–6146.2020.03.003

吴亚女, lin_xi1998@sina.com。

2019–10–16

(责任编校: 张红)