基于AFDD的悬索桥模态参数识别
2020-07-18严开军王尧伟单德山
严开军,王尧伟,何 淼,单德山
(1.中电建路桥集团工程设计研究院,北京 100048;2.西南交通大学桥梁工程系,四川成都 610031)
结构模态参数是掌握结构动力特性的基本参数,结构的模态参数识别一般分为理论、试验以及运营三大分析方法。其中频域的PP法[4]、FDD法[5]、EFDD法以功率谱为基础;时域随机子空间法则以状态方程为基础。单德山[1]等对模态参数识别的几种常见方法进行了对比分析,对一座斜拉桥进行了模态参数识别,并总结了各种方法的优缺点。王睿[2]等将稳定图融入到PP法原理中,识别了钢结构塔柱的模态参数。为降低噪声的影响,Brincker[3]等在PP法的基础上用奇异值分解了测量响应信号的功率谱密度矩阵然后识别到了模态参数,而且结果表明此方法对密集模态具有相对较好的识别效果。
在众多的模态参数识别方法中,频域法或多或少都需要人为干预才能得到结构的模态参数,这对于数据量较少的试验模态分析是可行的,但是运营状态下结构产生的连续实时响应数据是十分庞大的,要对如此庞大的数据进行带有很强的人为干预的模态识别显然是不可取的,而且人为干预带有很强的主观性,对密集模态也不好处理。时域法中的随机子空间方法虽然能得到较稳定的频率与阻尼比,但是计算效率相对低下。
为解决此问题,本文以频域分解法为基础,引入尺度空间方法,对奇异值曲线进行尺度空间缩放,最终形成具有峰值自动拾取的AFDD法。并以一座大跨度悬索桥为工程背景,选取符合结构模态参数识别要求的数据使用AFDD进行频率、振型以及阻尼比的识别,验证了方法的可行性与高效性。
1 工程背景
某地锚式悬索桥安装有长期实时健康监测系统,对结构长期的工作状况进行监测。该桥主梁上安装有14个竖向加速度传感器,7个横向加速度传感器。竖向加速度传感器布置在上下游的八分点,横向加速度传感器布置在上游的八分点,且竖向、横向加速度传感器都安装在靠近下平联的主桁上,单向加速度传感器编号及示意如图1所示,其中传感器记为:VIB-L**-X/Y/Z。其中VIB表示加速度传感器缩写;L表示钢桁梁代号;**表示传感器系统编号;X/Y/Z分别表示桥梁的顺桥向(以立面与平面图向右为正)、横桥向(以上游侧为正)以及竖桥向(向上为正)。为避免吊杆对加速度信号的影响,图示所有单向加速度传感器都布置在非吊点竖杆上。长期监测系统对加速度信号采样频率设为20 Hz。由于实桥长期监测系统受环境等不确定性因素干扰比较大,为减小干扰得到比较好的识别结果,本文在进行结构模态参数识别之前使用探索性数据分析(EDA)筛选出了质量较高的原始数据。
2 理论模态分析
本文采用大型通用有限元软件ANSYS建立有限元模型分析悬索桥动力特性,其中主梁采用beam4单元,主缆以及吊索使用Link10单元,索塔由于存在变截面使用beam44单元。主梁与索塔之间使用耦合约束模拟竖向支座以及横向抗风支座。有限元模型如图2所示。本文提取前2阶横弯模态以及前4阶竖弯模态与运营状态下识别得到的进行对比,提取结果见图3。
通过对上述ANSYS有限元的分析结果进行汇总,可以得到如表1所示的模态信息表。
通过对该悬索桥的模态信息表分析可知,主梁的前6阶振型都位于[0,1]Hz区间内,其在该区间内,共有4阶竖弯振型,以及2阶横弯振型,后续章节的AFDD计算将建立在此先验结果的基础上,通过将AFDD算法计算出来的频率、振型等模态参数与有限元模型的计算结果进行对比,进而验证AFDD算法实用性。
3 AFDD算法原理

图1 单向加速度传感器编号及示意(单位:m)
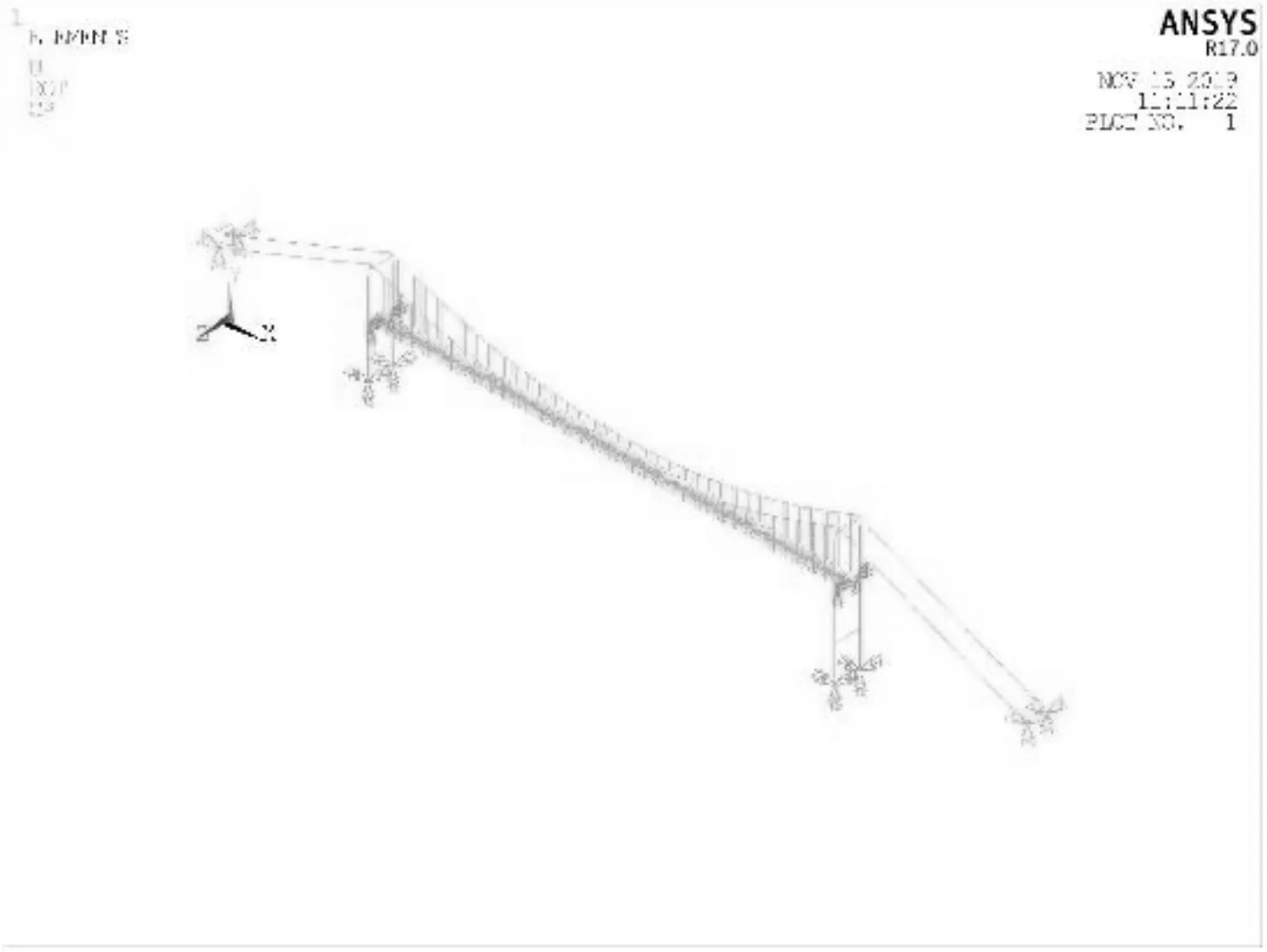
图2 某悬索桥有限元模型

表1 模态信息
3.1 FDD原理
频域分解法为对峰值拾取法(PP)的改进,其首先求出待分析信号的功率谱密度矩阵,其次对功率谱密度矩阵做奇异值分解(SVD),进而将多自由度系统转换为单自由度系统的叠加,进而识别结构的模态参数。
白噪声激励下频响函数Sxx为常数,定义复数βi:
(1)
对待分析信号求自功率谱密度函数为:
Syy(ωi)=βiψiψiH
(2)
功率谱密度矩阵Syy为Hermitian矩阵,即其奇异值分解结果与特征值分解结果一致,对功率谱密度矩阵Syy进行SVD分解,不为零奇异值的个数即为矩阵的秩(假设为r),有:
Syy(ω)=USVT=USUH
(3)
式中:U是酉矩阵,其中包含r个奇异值向量;S是由r个从大到小排列的正实数奇异值组成的对角矩阵。基于矩阵运算法则,特征频率对应的不为零奇异值个数应为1或着模态振型数。
比较式(2)和式(3)可知,对Syy进行SVD分解后,将多自由度系统分解成为单自由度系统的叠加,实现了多自由度系统的解耦。奇异值对应单自由度系统的功率谱密度函数,峰值点对应的频率即为单自由度系统的特征频率;奇异值向量即为特征频率对应模态振型的估计,由模态振型的正交性可知,当这些奇异值向量正交时,这种估计才能成立。
3.2 AFDD原理
自动频域分解法(AFDD)同频域分解法(FDD)类似,也是一种频域模态参数识别算法,其主要流程为:首先,求分析信号的功率谱密度矩阵;其次,对信号的功率谱密度矩阵做SVD分解,得到U、S、V矩阵;最后,通过峰值自动拾取算法得到奇异值曲线的峰值,以峰值点所在坐标确定振型以及阻尼比。
相对于FDD,AFDD增加了峰值自动拾取部分,进而减少了因人为选取峰值产生的误差,其原理主要为类似于小波变换的尺度空间方法,通过对奇异值曲线进行尺度空间的缩放,进而识别到较为密集的频率信息,AFDD的主要流程如图 4所示。

图3 频率振型提取结果

图4 AFDD算法原理
4 实桥信号模态参数识别
为了更准确地识别结构模态参数,以该大跨度悬索桥为背景,取该悬索桥2020年1月1日—2020年1月7日的主梁竖向及主梁横向加速度数据为分析内容,采用AFDD分析方法对该桥运营状态下长期监测系统的测试数据进行分析处理,以验证该算法对大跨度悬索桥模态参数识别的适用性。
4.1 频率识别
根据AFDD的算法步骤,计算得到2020年1月1日—2020年1月7日主梁竖向及横向加速度数据的功率谱密度曲线,因每天的功率谱密度曲线图形非常接近,故本章节仅展示2020年1月4日的主梁功率谱密度曲线,根据自动识别峰值算法,对主梁竖向及横向加速度的功率谱密度曲线求峰值,其中,根据有限元的先验计算结果,将主梁竖向峰值拾取个数均取为4,横向峰值拾取个数取为2,其中,竖向及横向的峰值拾取点对应的频率均分布在[0,1]Hz区间,故图形中频率轴仅展示[0,1]Hz,具体结果见图 5、图6。

图5 拾峰后的主梁竖向加速度功率谱密度曲线

图6 拾峰后的主梁横向加速度功率谱密度曲线
根据上述分析结果,对功率谱密度曲线的峰值拾取结果进行汇总,因可能存在模态混叠,故对拾取的频率进行基于振型相似度的MAC判别,对相似度较大的频率点进行了合并,最终频率分析结果如图7、图8所示,经观察发现,每天的频率分析结果较为接近,说明AFDD算法的频率计算效果较好,且在算法内部设定参数后后续不许人为干预。

图7 主梁竖向频率AFDD识别结果
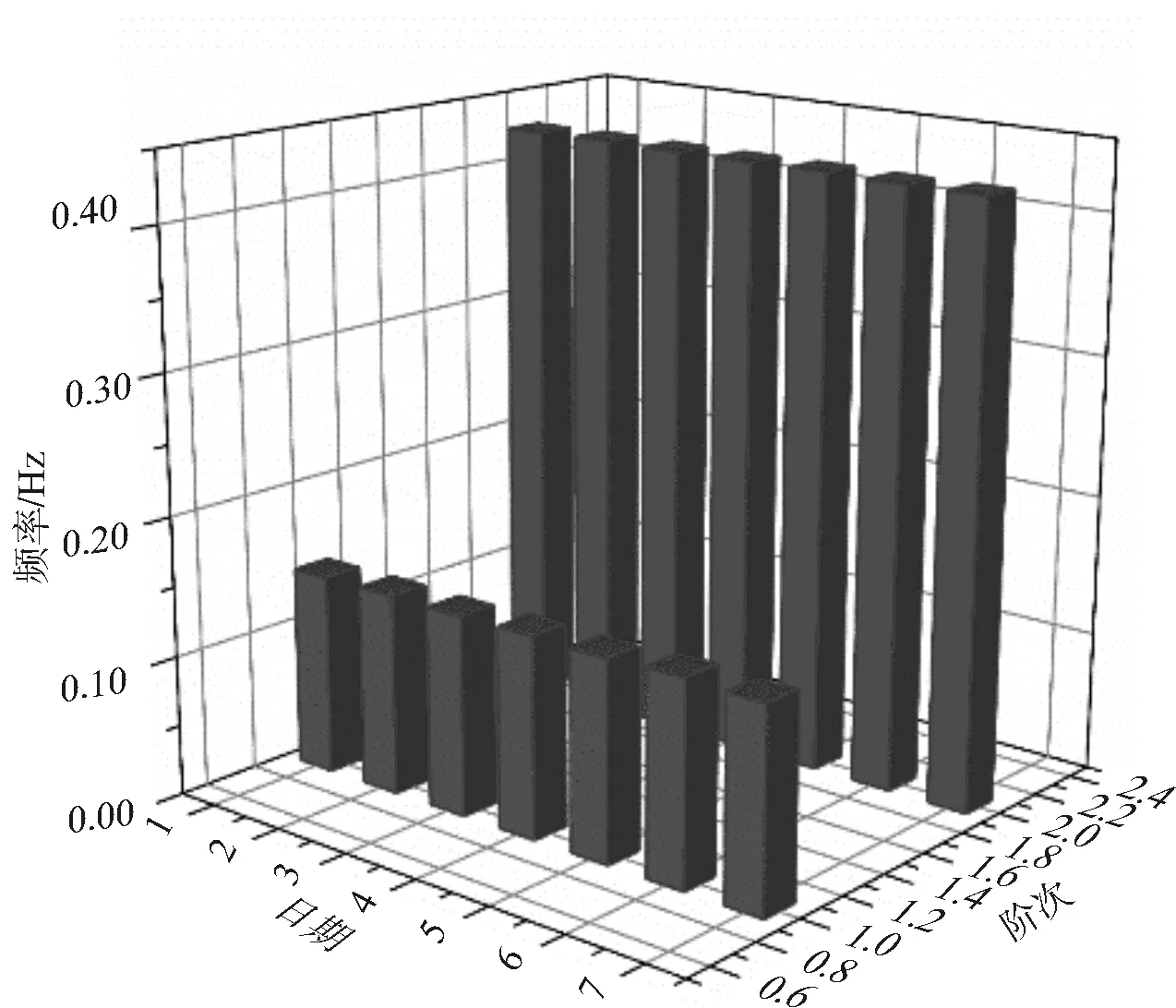
图8 主梁横向频率AFDD识别结果
4.2 振型识别
经过分析发现,AFDD算法能够识别出主梁竖向加速度的前4阶振型,以及主梁横向加速度的前2阶振型,因2020年1月1日—2020年1月7日的主梁横向及竖向加速度振型分析结果较为接近,故此处仅展示2020年1月4日的分析结果,主梁竖向及横向加速度数据的振型分析结果如图9、图10所示。

图9 主梁竖向振型AFDD识别结果
通过对图示的结果进行分析,AFDD计算出来的振型与ANSYS有限元的分析结果较为接近,但其对应的频率值仍然具有一定的误差,主要原因为有限元建模使用的是鱼骨梁模型,作为钢桁架与正交异性钢桥面组合结构在建模时未考虑桥面板对刚度的贡献,所以频率值存在偏小的情况。

图10 主梁横向振型AFDD识别结果
4.3 阻尼比识别
对2020年1月1日—2020年1月7日的主梁竖向及横向加速度识别的阻尼比进行汇总,如图 11、图12所示,通过观察图形中阻尼比数值的分布规律可知,AFDD法对阻尼比识别的精度较差,有待进一步研究提升精度。

图11 主梁竖向阻尼比AFDD识别结果
5 结论
基于某大跨度悬索桥健康监测系统一周的测试数据,本文利用AFDD算法进行了桥梁运营模态参数识别的研究,得到如下结论:

图12 主梁横向阻尼比AFDD识别结果
(1)AFDD在设定了相关参数后,后续的运算过程完全不需要人为干预,适应长期结构监测数据分析,自动化程度高。
(2)基于峰值自动拾取的AFDD法,能够较好地识别到代表桥梁信息的频率峰值点,识别精度高。
(3)AFDD的主梁竖向及横向频率识别结果,与ANSYS有限元的分析结果较为接近,分布规律一致,能作为大跨度悬索桥的模态参数识别。
(4)AFDD的主梁振型识别结果较为精确,MAC准则可以较好地进行振型相关性的判别。
(5)AFDD的主梁阻尼比的识别结果欠佳,有待进一步研究提升精度。
