由一道习题引发的反思

盛维林

（韶关学院 数学与统计学院，广东 韶关 512005）

常微分方程在科技理论中具有非常广泛的应用，是高等数学的重要内容之一［1］，一阶线性微分方程是其中重要的一类方程［2］.通常解一阶线性微分方程的方法有常数变易法［3-4］和积分因子法［5］.此外，一阶线性微分方程还有其他一些解法［6］.这些解法中，“常数变易法”是求一阶线性非齐次微分方程通解的最重要的方法［7］，但由于“常数变易法”过于巧妙，学生在做题时，还是会出现一些问题.在求解一道一阶线性微分方程的习题中，学生出现了四种不同的解法，其中有两种解法有别于常规解法，笔者对这些解法进行了分析和总结.

1 常系数变易法

一阶线性非齐次微分方程：

其中P（x），Q（x）是闭区间［a，b］上的连续函数.称：

为与（1）对应的一阶线性齐次微分方程.常系数变易法通常是先求出（1）所对应的齐次方程（2）的通解.因为方程（2）是可分离变量的微分方程，分离变量得，

两端分别积分，得：

即

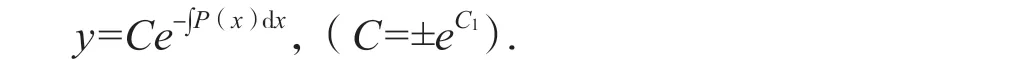
然后设y=C（x）e-∫P（x）dx为（1）的解，代入（1）求得C（x）=∫Q（x）∫P（x）dx+C，从而得到（1）的解.以上是课本上的推导过程.

2 一道习题引发的不同解法

在这节课的课后，笔者布置了以下这道题目作为课后习题［1］.求方程

的通解.

（5）式所对应的齐次方程为：

解法（一）：对（6）式分离变量、 两边积分得，

令y=e-x2+c（x）代入（5），得

解法（二）：对（6）式分离变量、 两边积分得：

解法（三）：（5）式变形为

分离变量、 两边积分得：

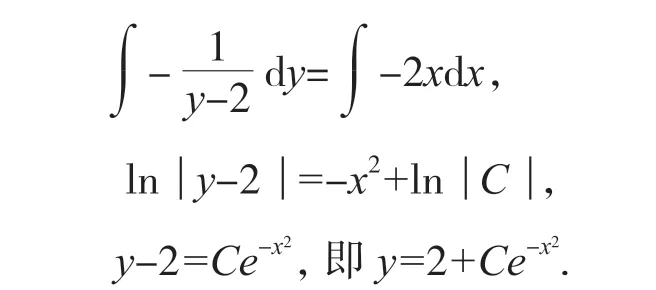
解法（四）：对（6）式分离变量、 两边积分得：

将y=C（x）e-x2代入（5）得C'（x）e-x2=4x.

所以（5）式的解为y=2+Ce-x2，其中C 为任意常数.

3 对这些解法的分析与思考

解法（一）、（二）、（四）都是用到了常系数变易法来解题，只是在解齐次方程（6）时出现了（7）、（9）、（11）不同的表示，导致后面代入求通解时也不同，转化为（8）、（10）、（12）求解C（x），显然（8）、（10）求解起来要比（12）复杂一些.其实解法（一）中（7）式令eC=C1，解法（二）中（9）式令那么后面的解法就和解法（四）一样了，但是即使这样做了，由于C1≠ 0，（7）、（9）与（11）比较就少了y=0 这个解.如果仔细分析会发现，解法（四）也少了y=0 这个解.问题出在哪里呢？就在两边同时除以y 时，没有讨论y 是否为0，应该分y=0 和y ≠ 0 来讨论，y ≠ 0 时是以上解答，其中C ≠ 0，由于y=0 也是解，所以将C 改为任意常数即可.虽然这样做比较麻烦，但对培养学生思维严谨性是有益的.后来笔者查看了几本《高等数学》的教材：《大学数学——微积分及其在生命科学、经济管理中的应用》第三版，谢季坚，李启文主编；《微积分》第三版，同济大学数学系编；《微积分》第三版，中国人民大学朱来义主编.这几本教材无一例外的都是直接两边除以y.另一本由东北师范大学数学系微分方程教研室编写的《常微分方程》中，是分y=0 和y ≠ 0 来讨论的.笔者认为这种处理方式比较妥当.

反观笔者的教学过程，在（3）式之前分离变量时讨论y=0 是齐次方程的解，y ≠ 0 时两边同时除以y，得到的C ≠ 0.由于C=0 时，y=0，所以将C 改为任意常数.紧接着让学生观察（4）式，如果把C1写成ln│C│（C ≠ 0）行不行?学生心里肯定产生疑问，可不可以这样做？为什么要这么做？先来回答第一个问题，提示学生考虑ln│C│的值域，这样做是可行的.为什么这样做？联想对数函数的运算性质，可以简化运算，很快得出y=Ce-∫P（x）dx（其中C ≠ 0）当C=0 时，对应的解为y=0，此时只需要将C ≠ 0 改为C 为任意常数即可.由于部分同学中学时对数函数的运算这里掌握得不牢固，导致在C1写成ln│C│时，所以出现解法（一）.解法（二）的出现是因为在解（3）式时，为了不节外生枝，没有说明如果负号放在y 这边的情形.但既然作业中出现了这个问题，就有必要跟学生澄清一下.回到（3）式，如果是改成则这里可以令C1=C（C ≠ 0），即y=Ce∫-P（x）dx，这样费一番周折之后还是与之前一致.因此，通过这道习题，可以跟学生强调，在解一阶线性微分方程对应的齐次方程时，如果有负号，负号不要放在y 那边，如果有系数，也不要放在y 那边.

反观解法（一）、（二），虽然有些不严谨的地方，但是也不是毫无意义，它们最终转化为（8）、（10）的解答，怎么解出C（x），这是一个很好的问题，让学生思考.第一步都是要将含有C（x）的项放在一边，由（8）得C'（x）eC（x）=4xex2，由（10）得得到然后解答这两个方程，这里要用到复合函数求导法则和除法法则才能求出来，这无疑也是对学生思维的一次挑战.通过对比，可以总结出，常规解法（四）的优越性，从而进一步强调常数C 的变形是有益的.同时对给出解法（一）、（二）的同学给予肯定.对于解法（三）的同学也要表扬，因为他们观察很仔细，这个方程可以看成可分离变量的微分方程，解答起来更简洁.

4 结语

一些教材限于篇幅和体系安排，比较注重传授知识，而对解决问题的思路分析就相对偏少.另外，会有一些细节的地方，可能考虑不到.这就需要老师平时用心钻研教材，精心设计教学.另外，在教学中总会出现意想不到的结果［8］，作为教师，不要盲目否认学生的思维，当出现非常规的解答时，教师应该认真反思，查找思维形成的原因.对一道习题多种解法的分析和总结，有利于拓宽学生的解题思路，提高学生探究问题的热情和学习高等数学的积极性，培养和发展学生的思维能力.