基于模糊PD 算法的竞速小车过弯策略研究
2020-07-17谢智阳庞项文
谢智阳,庞项文
(1.河源职业技术学院 机电工程学院,广东 河源 517000;2.河源市工业机器人技术应用工程技术研究中心,广东 河源 517000)
竞速小车按寻迹传感器进行分类大致包含光电传感器导航[1]、电磁导航[2]、CCD 摄像头导航[3]和激光雷达导航[4].光电传感器导航有成本低廉、易于实现等优点,一直以来都是简易寻迹小车的研究热点.竞速小车的成绩除受寻迹传感器的影响之外,尤为重要的是其控制算法的优劣会在竞速赛中起到关键性的作用,然而小车在直道行驶中很难体现出各自的差距,因此研究如何快速通过弯道是算法设计的重点.
文献[5]研究了在停车过程中采用了梯形规划曲线的停车策略,初步解决了停车过程中减速距离短、平稳性差的问题;文献[6]采用强化学习的方法在一定程度上解决了智能车路径认知的问题;文献[7-8]在智能车避障和多工况方面作了较深入的研究.鉴于前人对过弯策略研究的较少,可借鉴的经验很难从文献中找到,且缺乏系统性的研究策略.笔者以开源的Arduino UNO 单片机为控制核心构建了竞速小车,并用固定参数的PID 算法和模糊PD 算法进行了系统性的过弯策略研究.
1 系统总体设计方案
系统主要由Arduino UNO 单片机、八路光电传感器探测模块、陀螺仪模块、红外避障传感器、电机驱动模块和转向系统组成.Arduino UNO 单片机为主控模块,负责采集各种传感器的输入信号和控制算法的运算;八路光电传感器探测模块负责探测小车相对于赛道的偏离情况,并将探测结果反馈至主控单片机;陀螺仪模块负责探测小车的倾斜角,用以判断小车是处在平道、上坡和下坡3 种状态中的何种状态;赛道终点处设有障碍物,当红外避障传感器探测到前方有障碍物时,实现停车功能.
寻迹模块采用TCRC5000 红外传感器,红外传感器采集到路径信息通过比较器后直接传到MCU 进行处理,同时JY901 陀螺仪捕捉角度信号输入MCU,MCU 统一将各传感器输入数据进行综合判断、运算,并输出信号控制舵机及电机驱动模块BTS7970.
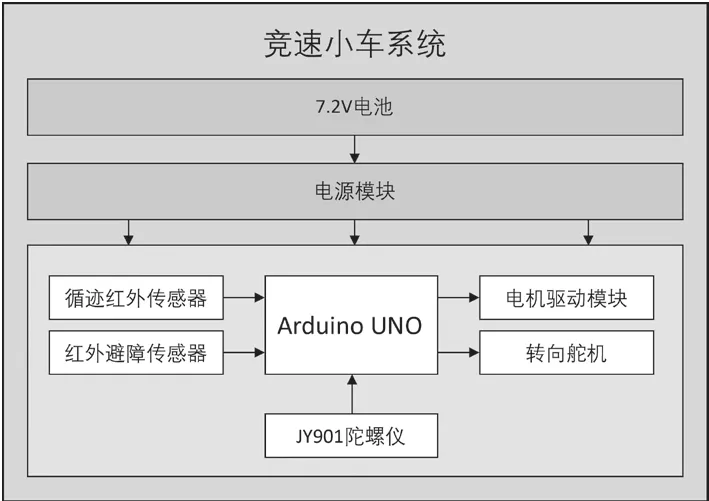
图1 系统硬件结构
2 硬件电路系统设计
2.1 电机驱动模块设计
电机驱动模块选用BTS7970,该电机驱动模块具有功率大、性能稳定、体积紧凑等特点,非常适合小车的电机驱动,其原理见图2.
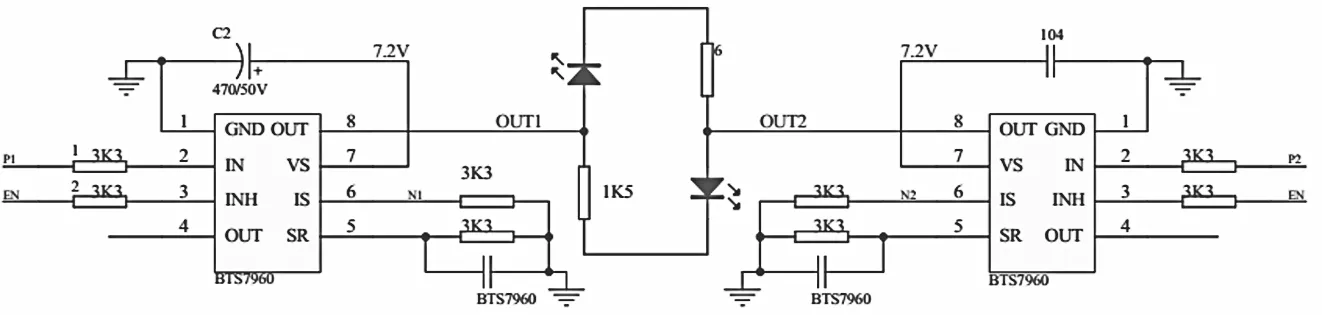
图2 单路电机驱动原理
2.2 寻迹模块的设计
八路光电传感器探测模块选用TCRC5000 红外模块,此模块集成度高、布局灵活、接线简易.为保证小车具有较好的前瞻性,寻迹模块安装在距小车前车轮9~10 cm 处.安装位置距离过长会导致小车上坡时与赛道发生剐蹭,到达坡顶时易丢失信号;距离过短会导致实时性不强,速度受限.探测模块共由八组红外光电传感器组成,根据本赛道的实际宽度,每组红外光电传感器的间隔为2.5 mm,具体布局见图3,若改变赛道黑线的实际宽度,则需重新调整红外光电传感器的间距.

图3 八路光电传感器探测模块布局
3 软件系统的设计
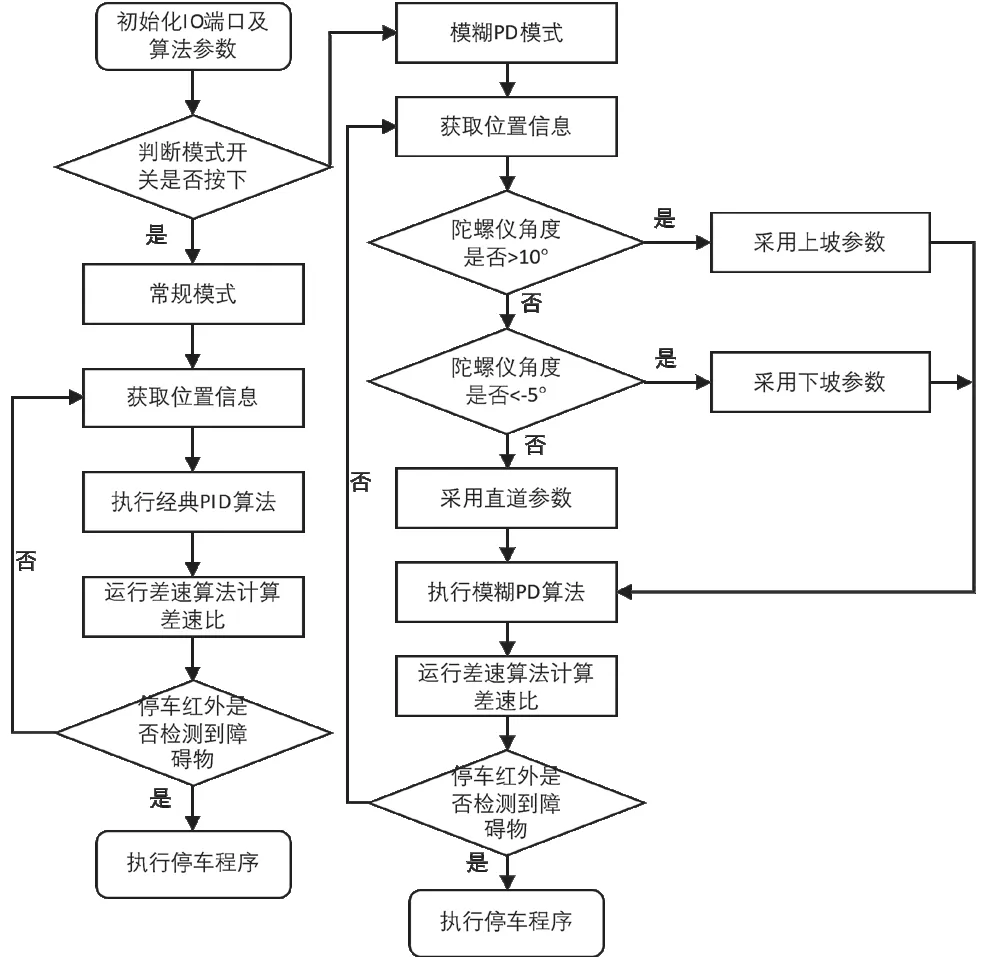
图4 软件系统结构
3.1 软件总体设计方案
在结合文献[9-12]的基础上,设计并优化本系统的控制策略,系统总体执行流程见图4.系统软件流程包含常规模式和模糊PD 模式,常规模式执行经典的固定参数PID 算法,模糊PD 模式则执行参数根据赛道实际情况参数可变的模糊PD 算法,且引入陀螺仪传感器,用以实现坡度检测功能,能有效防止小车因车速过快冲出赛道.
3.2 寻迹模块输入信号映射
TCRC5000 红外模块是开关量输入,即压黑线为低电平,没压黑线为高电平,因此只需读取相关IO 端口的电平状态便可获知相关传感器是否压到黑线,如想把零乱的8 个传感器的输入值反馈至控制算法中计算就必须对传感器输入的值进行组合量化排序.首先对与传感器连接的IO 端口进行初 始化,把IO 口设置成输入模式以读取传感器输入的高低电平信号,用for循环将8 组传感器的值存至一个八位数组里,并按表1 的映射关系进行映射,映射前,寻迹模块的探测精度为1/8,映射后的探测精度为1/15,在不增加硬件成本的情况下,将探测精度提升一倍,有效保证竞速小车行驶的稳定性.
3.3 差速策略
小车驱动电机采用BTS7970 电机驱动进行驱动,该电机驱动模块引出4 个引脚IN1~IN4 供用户操作,IN1 和IN2 控制左轮,IN3 和IN4 控制右轮.本文重点研究了如何在不脱离赛道的前提下快速通过弯道,处理方式主要是直道以正常速度行驶,在进入弯道时进行减速同时给予两个轮相应的差速以模拟真车的差速器来达到过弯时更顺畅快速,弯道的减速处理将传感器位置和电机进行关联,具体策略见公式(1).

公式(1)中V 为期望速度,即小车在该赛道上的上限速度;Kp为比例参数;error 为小车的方向偏离值.小车无偏离时,偏离值为0,误差随黑线偏离中间传感器距离增大而增大,一边误差为正一边为负具体偏离值的映射值见表1.
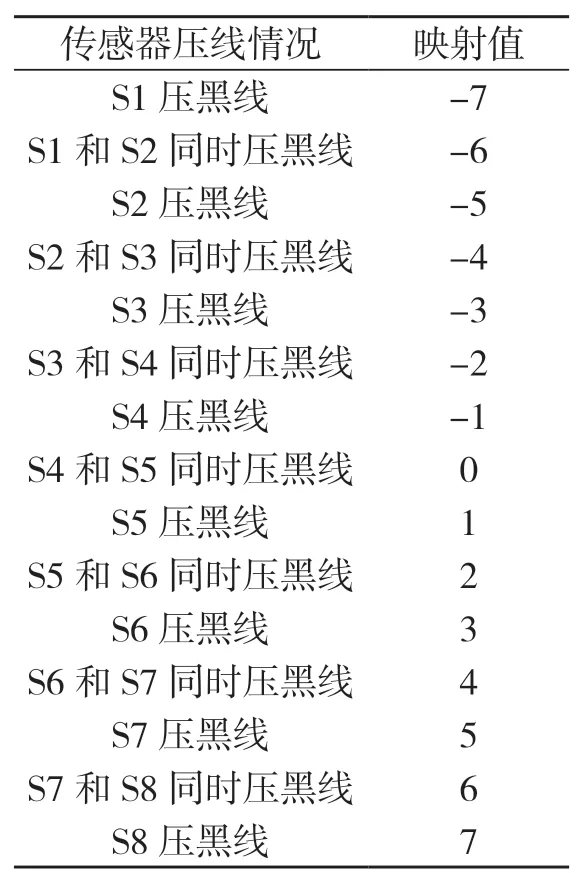
表1 传感器映射关系

表2 有差速的对应

表3 无差速的误差
由表2 和表3 可知,有无差速的各个误差的左右电机的PWM 对应关系,其差速与误差成一定的线性关系,会根据赛道的路况的变化而变化,具有一定的适应性,性能表现会比一般的等速过弯有显著的提升.
3.4 固定参数PID 算法实验
PID 参数整定过程是理论与工程实践经验相互结合的过程,实验前需结合小车模型大致推算出PID 参数的范围,工程实践中需反复调试参数进行实验分析,从而得到最佳的PID 参数组合.
PID 的经典公式为:
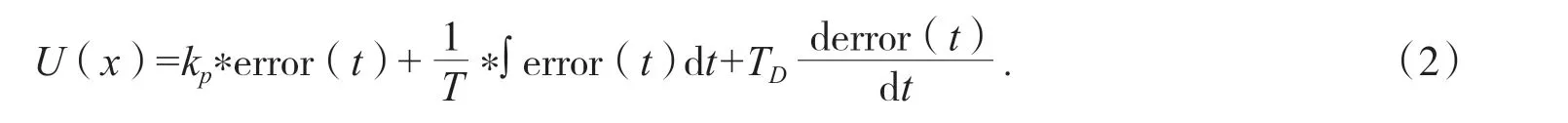
由图5 和PID 的经典公式可知,经典的PID 控制算法由期望值、反馈值、比例项调节参数、积分项调节参数、微分项调节参数和输出值构成.
由经典的PID 公式得出本文的数字PID 公式(3).
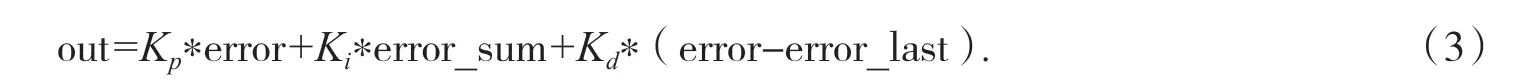
由公式(3)和图5 可知,PID 的输入为误差error、输出为舵机PWM 的关联值out,此值经换算后为舵机的PWM 值.
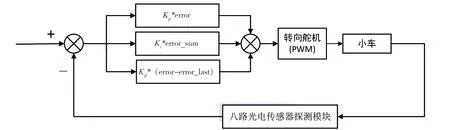
图5 本文数字PID 框架
第一步,整定比例参数Kp,此时微分参数和积分参数为零,即out=Kp*error,实验结果见图6.
由图6 可知Kp为7 时,整个系统的反应速度快,但震荡也较大,且震荡频率会相对较高.
Kp为2 时,整个系统的反应速度会变得非常缓慢,但到了引导线后波动不大,该参数的应变能力不强,不适合用于赛道.
本文采用比较折中比例参数,即Kp为4,从图6 可看到该参数在震荡和系统响应速度上都比较理想.
经实验分析,比例参数相对较大时,系统反应会迅速,但系统的震荡也会很大,误差会在期望值间来回震荡,整个系统显得很不稳定且效率低下,并不理想.而把比例值调到相对较小时,系统的反应就会相对缓慢,越小越慢,由于比例值小所以到了期望值后它的震荡不会很明显,但响应迟钝.增大Kp则响应快但震荡大,减小Kp则震荡小但响应慢,这是一个矛盾体,因此经典的PID 算法在Kp的基础上引入积分参数,当Kp调到系统适中的时候,固定Kp,紧接着调试Ki,具体见公式(4).
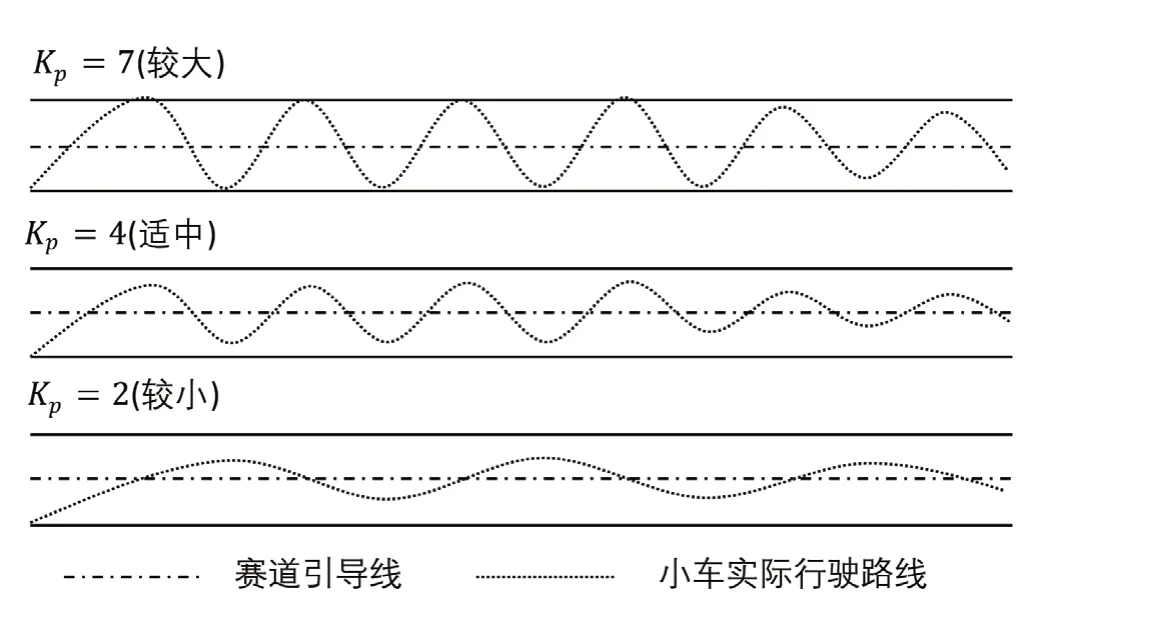
图6 比例值大小效果对比

公式(4)中的error_sum 是误差进行自我累加的结果,如果进行操作后误差还没消除,error_sum 便会愈加愈大,操控的力度也会愈大,直到消除误差,它便会渐渐减小,直至为0.积分参数在消除静态误差效果比较好,如果误差较大且短时间内修正不好的话,error_sum 便会累加到系统的极限,会超过相应的硬件的执行极限,导致系统崩溃,此时要进行积分分离处理,操作相对复杂.对此,选择屏蔽积分参数,即Ki=0.
其实只引入比例项参数Kp时,已经得到初步的寻迹效果,但想得到更好的过弯的效果,便要引入微分项参数Kd.本文重点对引入微分项参数Kd进行实验分析,见公式(5),通过实验得到最佳的微分项参数Kd.
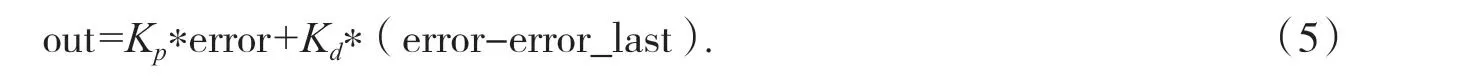
在Kp的基础上引入微分项参数Kd会起到预测变化、抑制误差增大的作用,弥补Kp比例的缺陷.微分简要的说是把当前误差与上次误差进行比较,来得出它的变化曲线、变化规律,再施加一定的阻尼力,让误差接近0 时减小调节力度,使小车可从震荡中恢复过来,增加动态稳定性,提高小车的抗干扰性.
3.5 模糊PD 控制器设计
由于赛道路况较复杂,若想获得极佳的过弯效果,固定参数的PID 算法还不足以适应复杂的赛道情况,为了得到更快的过弯速度,需对PID 算法参数进行简单的模糊化.经过多次实验分析,本文重点对PD参数进行实验整定,模糊控制器总体框架见图7.
模糊控制器的输入量为误差e 与误差的变化率ec,输出为PD 控制器的比例参数Kp和微分参数Kd的语言变量,本文的Kp、Kd的模糊子集为{负、零、正},模糊规则见表4,Z1 为激进PD 参数,Z2 为中等偏激进PD 参数,Z3 为中等折中PD 参数,Z4 为保守PD 参数,参数再根据计算和经验进行赋值.
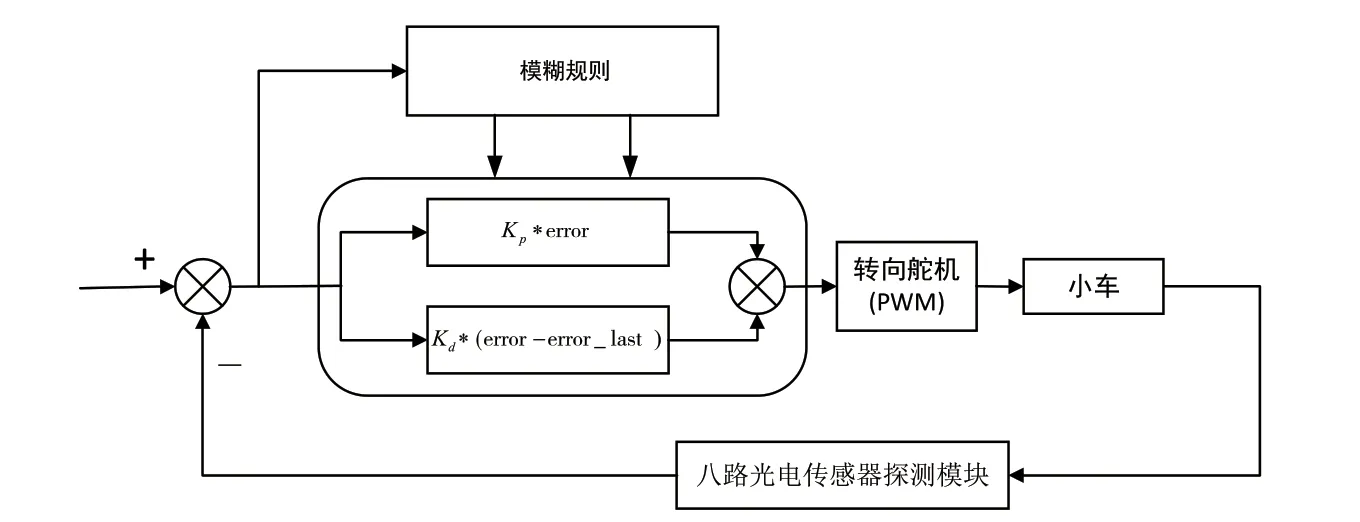
图7 模糊控制器架构
4 实验结果分析
单独运用固定参数的PID 算法并不能很好的适应赛道,在长直道入弯的时候由于惯性的作用使小车偏离赛道甚至有冲出赛道的可能,且过弯后恢复稳定的时间过长,并不适合该赛道使用,因此本文在固定参数的PID 的基础上加入了模糊规则,使系统具有一定的适应性.根据图8 的实验结果可知,相比于固定参数的PID 算法,模糊PD 算法能稳定、快速的通过弯道,且小车摆动幅度较小.
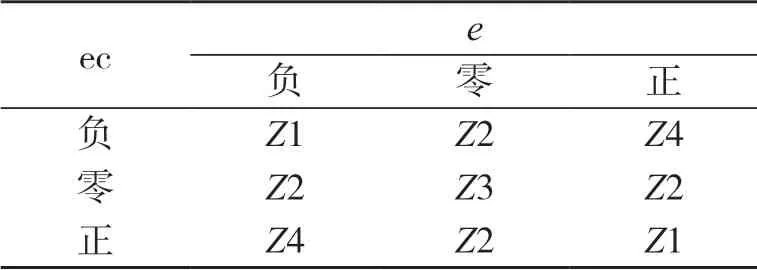
表4 模糊规则表
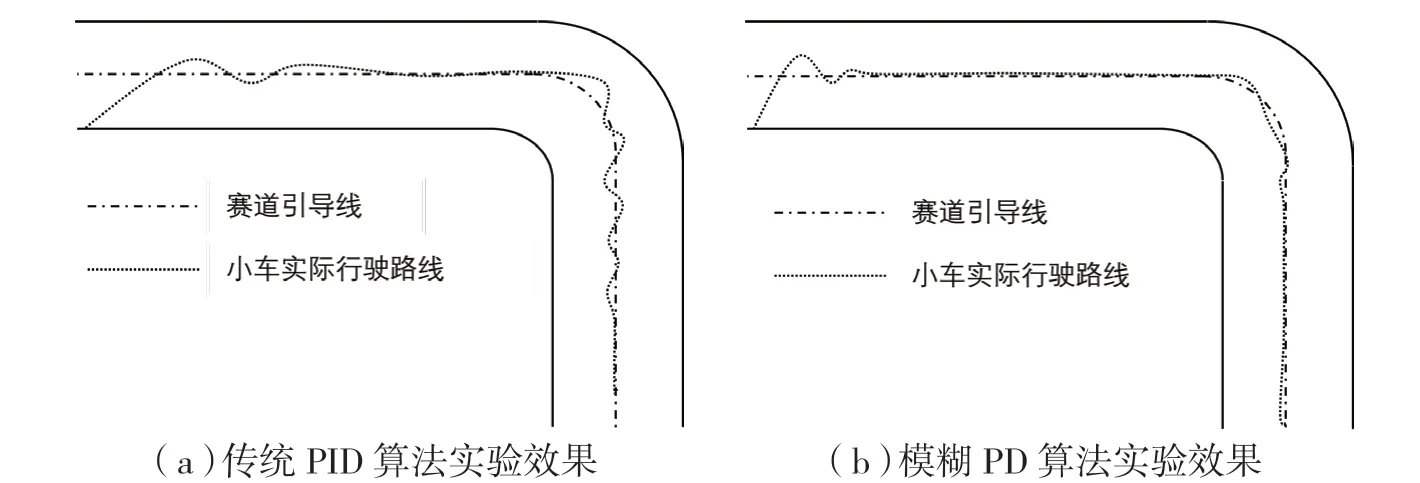
图8 模糊后的小车过弯行径
5 结论
(1)设计了由Arduino UNO 单片机、八路光电传感器探测模块、陀螺仪模块、红外避障传感器、电机驱动模块和转向系统组成的竞速小车.
(2)笔者分别从比例算法、固定参数PD 算法和模糊PD 算法进行了系统性的实验研究.实验结果表明,固定比例算法、固定参数的PD 算法在直道上与模糊PD 算法并无明显差异,而在弯道上模糊PD 算法明显优于固定参数PD 算法和比例算法.同时,给出了详细的调参过程和实验数据分析,为竞速小车过弯策略研究提供了重要的试验经验.
