一类有意识分类和控制策略的艾滋病性传播模型
2020-07-17刘小佑
代 帆,刘小佑
(南华大学 数理学院,湖南 衡阳 421001)
0 引 言
众所周知传染病是直接危害人类健康的重要因素之一,这其中就包括艾滋病(AIDS),它是一种危害极大的传染病。据WHO报道,艾滋病毒仍然属于一项全球主要公共卫生问题,到目前为止已造成3 200多万人死亡。2018年,全球有77万人死于与艾滋病毒相关的病症。目前仍没有针对艾滋病毒感染的治愈方法,但通过有效的抗逆转录病毒药物可使病毒得到控制且利于预防传播,从而使艾滋病毒感染者以及面临重大风险人员能够长期享有健康且有益的生活(见https://www.who.int/zh/news-room/fact-sheets/detail/hiv-aids)。艾滋病具有很强的社会危害性,会给个人、家庭和社会带来不可估量的损失。
到目前为止,已有许多专家学者对艾滋病的传播做了深入的研究,各种刻画艾滋病传播规律的数学模型也相继被提出来[1-7]。艾滋病的主要传播途径有血液传播、毒品注射传播、母婴传播和性接触传播。据中国疾控中心、联合国艾滋病规划署和世界卫生组织联合评估,性传播是主要传播途径,2017年报告感染者中经异性传播占比为69.6%,男性同性传播为25.5%(见http://www.chinacdc.cn/mtbd_8067/201811/t20181128_197565.html)。各种统计数据表明,性传播是艾滋病目前最主要的传播途径,且男男同性性传播占比逐年提高[8]。另外随着艾滋病防治和宣传工作的不断深入,如今人们对艾滋病的认识逐步加深,已有相关研究表明,人们对艾滋病的认识程度及主观防治意识等因素在艾滋病的防治中能起到一定的积极作用[9-14]。
基于上述原因,本文将考虑一类具有意识分类和控制策略的艾滋病性传播模型。该模型具有常数输入、指数死亡和标准发生率,将考虑性传播(包括男男同性)、意识分类和控制策略等主要因素。将所考虑的区域中总人口分为八类:
1)无意识易感者女性(Sf)(没有艾滋病防治意识,可能会无意间经过性接触传播途径成为无意识感染者女性);
2)无意识易感者男性(Sm);
3)有意识易感者(Sa)(有艾滋病防治意识的易感者,不会主动参与任何有风险的艾滋病感染行为);
4)无意识感染者女性(If)(没有艾滋病防治意识且不知道自己已经感染的女性感染者,可能会无意间经过性接触感染他人);
5)无意识感染者男性(Im);
6)有意识感染者(Ia)(有艾滋病防治意识的感染者,不会主动感染别人);
7)艾滋病患者(A);
8)接受治疗的感染者(T)(有意识感染者中通过艾滋病防治意识宣传教育后开始接受治疗的感染者,该类人群不会参与任何与艾滋病传播有关的行为)。
该艾滋病性传播(包括男女异性和男男同性)模型的主要假设为:
1)新加入人口都为成年人,不考虑垂直感染;
2)新感染者都是无意识的感染者;
3)艾滋病只在无意识易感者和无意识的感染者之间传播;
4)国家及社会在艾滋病防治意识及治疗等方面采取相关干预控制策略。
具体模型如下:
(1)
模型(1)中各参数的意义如下:
Λ:人口输入常数;
ε:女性输入比例为(0<ε<1);
N:总人口数,也即N=Sf+Sm+If+Im+Ia+A+Sa+T;
d:自然死亡率;
τ:因病额外死亡率;
θ:感染者从无意识向有意识的自然转化率(即通过自身身体变化,自主意识到感染艾滋病毒的概率);
δ:艾滋病感染者成为艾滋病患者的转化率;
η:接受治疗的感染者成为艾滋病患者的转化率;
β1:无意识易感者女性(Sf)和无意识感染者男性(Im)之间的有效接触率;
β2:无意识易感者男性(Sm)和无意识感染者女性(If)之间的有效接触率;
β3:无意识易感者男性(Sm)和无意识感染者男性(Im)之间的有效接触率;
控制强度系数p1:无意识易感者女性(Sf)通过艾滋病防治意识宣传教育成为有意识易感者(Sa)的转移率;
控制强度系数p2:无意识易感者男性(Sm)通过艾滋病防治意识宣传教育成为有意识易感者(Sa)的转移率;
控制强度系数q1:无意识感染者女性(If)通过艾滋病防治意识宣传教育成为有意识感染者(Ia)的转移率;
控制强度系数q2:无意识感染者男性(Im)通过艾滋病防治意识宣传教育成为有意识感染者(Ia)的转移率;
控制强度系数q3:有意识感染者(Ia)通过艾滋病防治意识宣传教育成为接受治疗的感染者(T)的转移率。
1 模型平衡点的存在性
为方便起见,引入记号a1=δ+θ+d、a2=δ+d、a3=τ+d。模型(1)的平衡点EP=(Sf,Sm,If,Im,Ia,A,Sa,T)可通过求解下面方程组得到。
(2)
若Im=0,可得
If=0,Ia=0,A=0,T=0,
即模型(1)有无病平衡点,其各项的值由上式表示,该无病平衡点记为
EP=(Sf′,Sm′,0,0,0,0,Sa′,0)。
若Im>0,可推出
以及一个关于Im的一元二次方程
(3)
其中
若方程(3)有正解Im,则模型(1)有地方病平衡点,并记其为
通过计算,可定义基本再生数[15]为
定理1若0
证明:把方程(3)中常数K改写成
K=-Q(R0-1)。
另引入一元二次函数
显然S(Im)=R0与一元二次方程T(Im)=0同解。一元二次函数S(Im)开口向上,且有S(0)=1,其顶点坐标为(Im-min,Q(Im)-min),其中
若0 因而有 由一元二次函数图像可知方程S(Im)=R0无正解,即模型(1)无地方病平衡点。 首先给出一个下文中将要用到的稳定性判定定理。 引理1若方程组的系数矩阵的所有特征值均具有负实部,则方程组的零解是渐近稳定的[16]。 计算可得方程组(1)的Jacobian矩阵为 (4) 定理2若0 证明:由矩阵(4)可得模型(1)在无病平衡点处的特征多项式为 当0 计算可得特征方程为 (5) 其中 显然有L>0和H>0。将方程组(2)中第4式的变形式 代入M中可得 现在讨论特征方程(5)中因式λ2+(L+M)λ+LM-H。考虑以下一元二次方程 x2+(L+M)x+(LM-H)=0, 其判别式 Δ=(L+M)2-4(LM-H)=(L-M)2+4H>0。 另据韦达定理有 x1+x2=-(L+M)<0。 为方便计算,引入 L=B+C,M=D+E 其中 则有 x1x2=LM-H=(B+C)D+BE+CE-H。 (6) 可得 CE-H=0。 故最后可得 x1x2=LM-H=(B+C)D+BE>0。 这表明特征方程(5)中二次因式项有两个负实根。 综上可知特征方程(5)存在8个负实根,满足引理1,故定理成立。 本文考虑了一类具有意识分类和控制策略的艾滋病性传播(包括男女异性和男男同性)模型。通过分析与计算,给出了模型的基本再生数,证明了模型的无病平衡点和地方病平衡点的存在性及其稳定性。其中基本再生数表达式为 从基本再生数的表达式中可以发现,三类性接触的有效接触率(β1、β2和β3)越小,则基本再生数也相应越小。另一方面,控制变量p1、p2、q1和q2越大,相应的基本再生数也会越小,也就是干预强度越大、控制策略越多,相应的疾病流行趋势就会降低。 本文主要限于考虑模型(1)平衡点的存在性及其稳定性,在后续研究中,将考虑它的最优控制问题。2 模型平衡点的稳定性

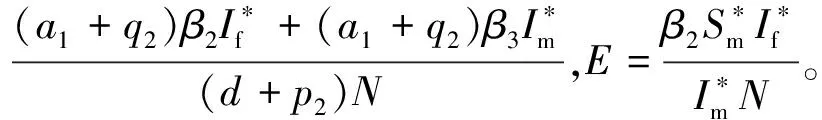
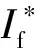
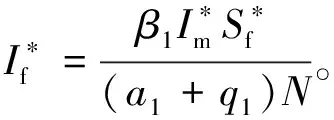
3 结 论
