风量罩测量球形喷口的模型优化与数值模拟研究
2020-07-17王汉青李铖骏窦秀敏
吴 祥,谢 东*,王汉青,李铖骏,窦秀敏
(1.南华大学 土木工程学院,湖南 衡阳 421001;2.南华大学 建筑控制技术湖南省重点工程实验室,湖南 衡阳 421001)
0 引 言
为了调节高大空间的温湿度,控制污染物浓度,改善室内的空气品质,需要对室内引入足够的风量。而通风系统的平衡与否直接影响系统的能耗,为了满足各个区域的风量设计要求并实现通风和空调系统的高效节能运行,常常通过测量风量对通风和空调系统进行风平衡调试[1-2]。风量测量的方法主要分为:风管内测量和风口测量。目前国内外学者对于风量测量的研究主要集中风管内的测量优化而风口的风量测量鲜有研究。均速管以其优越的性能被广泛运用于管内风量的测量,因此提高均速管的测量精度成为大部分学者的研究目标。C.Can[3]研究了在均速管(averaging pitot tube,APT)下游设置的空气阻尼器后对配风系统管内风量测量的影响,提出相应的数学模型并对均速管(APT)流量计算公式进行修正,提高了流量测量精度。M.Kabacinski[4]建立了均速管(APT)静压口和全静压口周围流动的数学模型,并进行了求解。利用数值模拟的结果对均速管(APT)的几何结构进行了优化。J.L.Zhang[5]提出了新型的均速管结构,对其周围的气流流动建立了数学模型,给出了流线和管道周围压力的分布,并测试了其性能。夏南琪[6]基于方形均速管流量系数的理论公式,提炼出结构参数检测杆横截面当量直径、静压孔中心与检测杆横截面中心角度两个关键参数,采用正交试验方法设计了方形均速管流量系数主效应因素试验,并以不同试验目标参数设计了主效应因素水平对比试验,确定了方形均速管的最优结构形式。刘亚成[7]根据均速管流量计的工作原理,分析均速管横截面当量直径、静压孔角度和风管平均流速这三个因素对均速管流量系数的影响,根据正交试验理论设计了CFD数值仿真试验,对迎流角的角度、迎流边的形状、背流边的形状和长度以及取压口的大小和形状进行了优化研究。毛新业[8]通过研究矩形管道中流体流动的特点提出了不同的矩形大管道风量测量方法,并对不同方法进行了比较分析。风管内风量的测量技术发展已经较为成熟,但关于风口风量的测量研究还相对较少。现有的风口风量测量方法主要有风速仪法和风量罩法[9],孙旭灿[10]利用标准风洞试验台对测定风速计算风量的修正系数进行了实验研究,对格栅式风口进行了不同风量、测试距离、测试仪器和计算面积的修正系数实验;王成凤[11]针对市场上常用的几种风量罩体进行实验,分析了罩体的选择及不同摆放位置对双层百叶风口测量的影响;罗运有[12]介绍目前风口风量的测量方法和特点,分析风量罩罩体阻力对风机盘管送风口测量结果的影响,研究表明风量罩的罩体阻力使得风口风量降低约1.0%。随着时代的发展,大空间建筑越来越多,大空间主要采用球形喷口送风[13],而球形喷口风量测量的精确度没有相关研究,为了实现系统的高效节能运行,同时达到精确控制室内环境的目的,研究球形喷口准确测量的方法是十分必要的。
1 模型建立
1.1 几何物理模型
为了提高网格离散效率及数值计算精确度,对风量罩测量球形喷口风量模型进行简化,如图1(a)所示,该模型由风量罩(分为罩体段和基座段)、喷口段和风管段组成。风量罩的基座简化为长度为260 mm,直径为400 mm的圆筒,而在基座的中间设置有测量风量的矩阵测量支架,其简化模型如图1(b)所示,长度为20 mm,宽度为10 mm,在测量支架的两侧设有接收测量风量所需的全、静压孔,各有16个测点,测点位置如图1(c)所示;风量罩的罩体段一端连接基座段,另一端连接喷口段,罩体的罩口由610 mm×610 mm的矩形接口构成;喷口段将球形喷口装饰圈、壳体忽略,仅保留球形喷口的流体域,简化后的球形喷口喉部曲率与实际球形喷口一致,其简化模型如图1(d)所示;风管段一端连接球形喷口,一端设置进风口,风管的直径与球形喷口的入口直径一致,长为1 500 mm。
1.2 数学模型
1)模型假设
因风量罩测量球形喷口风量的过程是湍流流动过程,为简化其复杂性,做如下假设:(1)流体域内空气为定常不可压缩流体;(2)不考虑风管温降,流动过程为等温稳态湍流流动;(3)风管的进风口气流为均匀的紊流速度入口;(4)测量过程密闭性良好,进出口满足质量守恒。
2)控制方程
本文采用Realizable k-ε两方程湍流模型对流动空气的三维稳态湍流流动进行数值模拟。
3)测量相对误差评价指标
相对误差是用来说明测量精度的高低。测量球形喷口风量的相对误差计算公式[14]如下:
(1)
(2)
(3)
式中:γ风量测量的相对误差值,%;Qs为实际风量值,m3/h;Q为采用风量罩测量的风量值,m3/h;A为风量测量断面的面积,m2;v为测点的平均速度值,m/s;α为测量支架的流量系数值,无量纲数;ρ为流动空气的密度值,kg/m3;ΔP为测量支架前后测点的全静压差值,Pa;Pq,i为测量支架前各测点的全压值,Pa;Pj,i为测量支架后各测点的静压值(Pa);N为测量支架全压或静压的测点总数。
1.3 数值求解
本文采用非结构化网格对计算区域进行划分,对喷口和测量支架速度等梯度较大的地方进行网格加密处理,模型的网格数量均在80 W以上。离散方法采用SIMPLEC的压力-速度耦合算法,动量、k和ε都采用二阶迎风格式。数值模拟的边界条件设置如表1所示。
1.4 模型实验验证
模型实验验证根据在不同风量下采用风量罩测量的测试风量与通过数值模拟在测量断面计算得到的模拟风量进行对比,如图2所示。其中不同工况下的模拟参数如表2所示,风量值通过不同实验工况在风管中采用毕托管多组测量后取的平均值,而对应的模拟入口速度根据测量的风量计算得出。
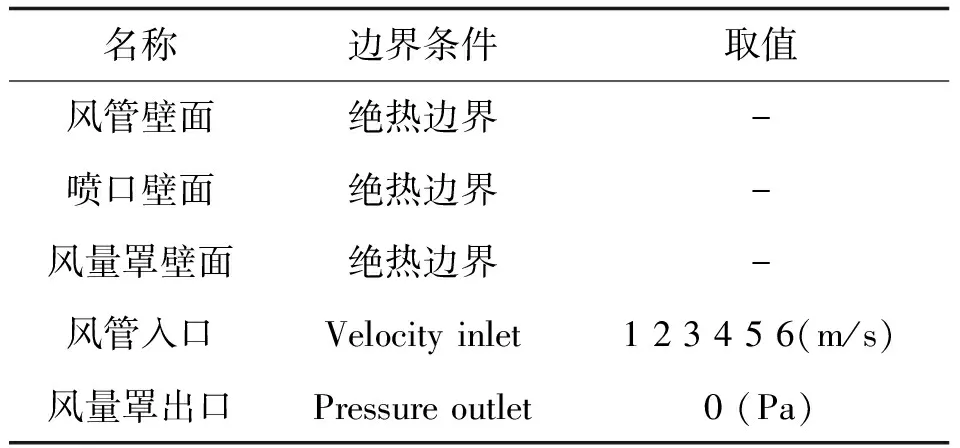
表1 数值计算边界条件设置
从图2可知,模拟风量与测试风量的数据匹配度较高,模拟的相对误差为10%~11.5%,误差原因在于本文对风量罩和喷口结构进行了简化,同时实验仪器也存在一定测量误差。对比数据验证了本文数值模拟所选用湍流模型及边界条件设置的正确性。

表2 实验验证的模拟参数
2 现有风量罩测量的误差分析
现有风量罩测量的误差分析是通过对现有风量罩测量球形喷口进行数值模拟,通过对罩体内的速度分布、矢量分布、压力分布以及不同风速下的测量误差进行分析,总结现有风量罩测量球形喷口风量精度低的原因。
图3为入口速度2 m/s时y=0和z=0剖面的速度分布图,可以发现,在入口速度均匀分布时,同时不考虑风管温降,喷口出口的球形喷口射流在罩体中y=0和z=0剖面速度分布基本一致,趋于轴心对称;测量支架区域的速度分布从中心到边缘有较大的下降趋势且存在明显的“断层”现象,这是由于球形喷口射流直接轴向喷射到测量支架上,到达测量支架时射流仍未扩散到罩体壁面上,罩体对球形喷口射流没有起到引流作用,同时核心速度的衰减程度不够,导致测量支架中心区域的速度与测量支架边缘的速度相差较大。
图4为入口速度2 m/s时y=0和z=0剖面的矢量图,可以看出,球形喷口射流在罩体中y=0和z=0剖面矢量分布趋于一致,同时结合两个剖面可以明显发现,喷口出口的球形喷口射流直接罩体出口的中心区域流出,而罩体出口的边缘区域存在少量的外部气流回流,这与风量测量的流动需求严重不符,将可能导致出现较大的测量误差。
图5为入口速度2 m/s时不同剖面的压力分布图。x=0剖面是测量支架的迎风面,输出测量断面各测点的全压值,从该剖面全压分布可以看出,最内环测点的全压值在10 Pa左右,而最外环测点的全压值0 Pa,这是由于球形喷口射流仅从迎风面中心区域流过,气流的动压值转化为测点的全压值,导致迎风面内环测点的全压值相差较大;x=-0.02剖面是测量支架的背风面,输出测量断面各测点的静压值,从该剖面全压分布可以看出,最内环测点的静压值在-4 Pa左右,而最外环测点的静压值为-0.1 Pa,这是由于罩体出口的边缘区域存在少量的外部气流回流,使得外环的静压值大于内环值的静压值;结合x=0和x=-0.02剖面可以发现,内环测点得到的全静压差远远大于外环测点得到的全静压差值,大约在14倍左右,使得从各测点得到平均全静压差值偏大,测量得到的风量值远远大于实际风量值。
图6为在不同风速下的风量与模拟风量以及风量测量相对误差值,由图6可知,随着入口风速的增加,模拟风量均大于实际风量,而不同风速下的相对误差值均趋于58%左右。说明采用现有风量罩测量φ250球形喷口的风量时,测量的风量值偏大,实际风量的大小对测量相对误差影响不大,相对误差值均在58%左右,即测量风量值是实际风量的1.58倍左右,测量结果无法满足工程实际的测量要求,按该风量罩测量结果对通风系统进行调试可能导致作用区域的控制参数远远达不到设计要求。
综上所述,采用现有风量罩测量φ250球形喷口风量时测量的相对误差在58%左右,测量误差与实际风量无关,而测量误差主要源于现有风量罩结构的不匹配,对球形喷口射流没有充分的衰减导流作用,气流无法在测量位置上呈现相对均匀分布,内外环测点间的数据相差较大,导致测量精度低。
3 风量罩模型优化研究
3.1 模型优化策略
通过对球形喷口风量测量的误差分析结果可知,要提高测量精度,需对风量罩进行结构优化,使气流在测量位置上均匀分布。球形喷口射流在断面上呈圆形分布,为了使罩体更好的导流,首先将罩体优化成圆台型。考虑到影响测量位置气流分布的因素主要为:罩口直径D1、罩体长度L以及基座直径D2,为了减少计算量,采用正交表L9(34)[15]进行风量罩结构优化模拟,其中三因数三水平的取值如表3所示。而测量方法对测量误差影响较小,为了简化模型,忽略现有风量罩的测量支架,并在相同的测量断面上根据《公共建筑节能检测标准》采取圆环法选取不同结构模型的测点位置和测点数目[16],模型优化的示意图如图7所示。
3.2 试验方法
根据正交表L9(34)设计9种不同的风量罩优化结构,并建立风量罩测量球形喷口风量的优化模型,依据前文所述的数学模型和数值求解方法,同时以风管入口速度为2 m/s对模型进行数值模拟,将模拟得到的测量相对误差γ作为正交设计的试验指标。

表3 L9(34)三因数三水平取值表
3.3 正交试验结果分析
表4为L9(34)正交试验直观分析计算表,从表4可以看出,A因素的第3个水平的测量相对误差均值最小,B因素的第3个水平的测量相对误差均值最小,C因素的第1个水平的测量相对误差均值最小,因此正交试验设计的最佳水平组合为A3B3C1,即当罩口直径D1为600mm、罩体长度L为1 000mm和基座直径D2为200mm时风量罩测量球形喷口的相对误差值最优,精确度最高;根据极差的大小可知,影响测量相对误差的主次顺序为基座直径D2>罩体长度L>罩口直径D1,其中基座直径D2对于测量误差的影响最大。
图8为各因素在不同水平的相对误差均值变化趋势,可以发现1)随着罩口直径D1的增加,相对误差均值先增大后减小,说明较小或较大的罩口直径D1都有利于风量测量,这是因为较小的罩口直径有利于更早对球形喷口射流进行束缚作用,而较大的罩体直径形成的导流角更大,更有利于导流;2)随着罩体长度L的增加,相对误差均值不断减小,说明罩体长度L越长,测量结果越好,这是因为罩体长度的增加有利于球形喷口射流核心速度的衰减,球形喷口射流运动距离越长,气流在断面的分布将越趋于均匀;3)随着基座直径的增加,相对误差均值增加,增加跨度较大,说明基座直径的选择是影响测量误差的关键因素,基座直径越小测量结果越好,但风量罩所产生的阻力也会增加,可能产生额外的阻力误差,因此提高测量的精确度应先选择与风口相匹配的较小基座直径。

表4 L9(34)正交试验直观分析计算表
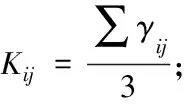
3.4 优化后的风量罩模拟结果分析
通过正交试验结果分析得到优化后的风量罩结构为:罩口直径D1为600 mm、罩体长度L为1 000 mm和基座直径D2为200 mm,以风管入口速度为2 m/s对优化后的模型进行数值模拟。
图9是优化后的风量罩在入口速度为2 m/s时y=0和z=0剖面的速度分布图,从图9可以发现优化后的模型在测量位置区域的速度分布从中心到边缘的下降趋势明显的改善且“断层”现象已经消失,罩体对球形喷口射流有一定的引流作用,测量支架中心区域的速度与测量支架边缘的速度相差较小。
图10为优化后的风量罩在入口速度为2 m/s时y=0和z=0剖面的矢量图,可以看出喷口出口的球形喷口射流从罩体出口的整个断面流出,已经不存在外部气流回流现象,已符合风量测量的流动需求。
图11为优化后的风量罩在x=0剖面的速度与动压分布图。优化后的模型根据x=0剖面上各测点的速度或动压来计算测量的风量值,从该剖面速度和动压分布可以看出,内环测点的速度和动压分别在3.8 m/s和9 Pa左右,外环测点的速度和动压分别在2 m/s和3 Pa左右,内外环测点动压值相差3倍左右,与现有风量罩的相差14倍相比,各测点的相对均匀度已大大提升,通过输出各测点的数据计算风量测量的相对误差为0.12%,这说明风量罩结构对球形喷口风量测量的影响已基本消除。
4 结 论
通过对风量罩测量球形喷口风量的误差分析以及测量优化的数值模拟研究可知:
1)现有风量罩测量φ250球形喷口风量时测量的相对误差在58%左右,测量误差与实际风量基本无关,而测量误差源于现有风量罩结构与风口不匹配,对球形喷口射流没有充分的衰减导流作用,气流无法在测量位置上呈现相对均匀分布,内外环测点间的数据相差较大,导致测量的精度低。
2)影响风量罩测量球形喷口风量精度的主次顺序为基座直径>罩体长度>罩口直径,优化风量罩结构以准确测量球形喷口风量时应优先考虑与风口相匹配的较小基座直径,同时选择合适的罩体长度和罩口直径。
3)正交优化后的风量罩测量φ250球形喷口风量的相对误差为0.12%,说明通过罩体结构优化可以解决现有球形喷口风量测量精度低的问题。
