团簇Ti3Al3的磁性及自旋密度研究

方志刚，王君奥，陈 林，李历红，秦 渝

（辽宁科技大学化学工程学院，辽宁鞍山 114051）

粒子的磁性在量子力学中与磁矩有关，磁矩可以从电子自旋角动量与轨道角动量两个量和一些与粒子有关常数的乘积求得，而磁性就是由分子磁矩有序排列所产生的。另外，分析电子自旋密度的分布也可以得出物质的磁学性能，进而分析出物质的稳定性能[1-5]。近年来，研究Ti-Al体系的学者越来越多，如Ramos和Reveles等人研究双金属Ti、Al亚纳米团簇中储氧[6],Quanlin Shi和Botao Qin等人对热爆炸反应制备的Ti、Al金属化合物的合成与性能进行了研究[7],Ramos和Arasa等人分析了Ti包覆Al表面的加氢脱氢[8]。Ti-Al化合物的相关研究虽然在许多方面已经取得了一定的进展，但是仍然有许多问题尚未解决，如Ti-Al体系的电子自旋态密度与磁性、Ti-Al体系的热力学等。如今非晶态合金是一种高新技术材料，被称为跨世纪的新型功能材料，具有极其优秀的物理、化学和力学性能,在电力、通信、航空等高新技术领域有重要作用，目前该体系市场需求量大，产业化前景广阔。本文利用密度泛函理论，通过分析各原子的磁距和各轨道的电子自旋态密度图，研究团簇Ti3Al3的磁学性质，希望能够为非晶态合金Ti-Al的深入研究提供理论支撑。

1 模型和计算方法

首先依据拓扑学原理[9]，设计二、四重态中团簇Ti3Al3可能存在的所有构型，并采用含相关校正的密度泛函理论（Density functional theory，DFT）[10-11]中的B3LYP/Lan12dz[12]进行一系列的全参数优化、频率计算以及验证，排除含有虚频或重复的构型，最终得到其优化构型。计算时对金属Ti、Al原子采用Hay等人[13]的含相对论校正的有效核电势价电子从头计算基组，即采用18-eECP的双ξ基组，以上计算均采用Gaussian09程序在启天M7150微机上完成。

2 数据分析及讨论

2.1 优化构型的结构

图1为经过全参数优化计算后得到的9种最终构型：戴帽四角锥（1（4））、戴帽三角双锥（1（2）、2（4）、2（2）、3（4）、4（4）、4（2）、5（2））以及四角双锥（3（2））3种构型。以1（4）的能量为零点，将这些优化构型按照能量由低到高进行排序，右上角的数字代表多重态。

2.2 团簇Ti3Al3的磁学性质

2.2.1 原子轨道的成单电子数

在3d过渡金属（如Fe、Co、Ti等电子排布时最后一个电子排在3d轨道上的原子）及合金中，由于轨道冻结，它的磁矩仅依赖于自旋磁矩。像电子、质子一类的基本粒子会因自旋而产生自旋磁矩，磁矩的方向与粒子的自旋方向相同。因此想要研究团簇Ti3Al3的磁学性质，首先要研究各原子不同轨道上的电子成单情况。根据自旋多重度的定义，二重态有1个成单电子、四重态有3个成单电子，因此团簇Ti3Al3的优化构型中二、四重态共9种构型均有磁性。表1表示了s、p、d轨道上的成单电子数。对于成单电子，根据其自旋方向可以划分为自旋向上的α电子（用正值表示）和自旋向下的β电子（用负值表示）。首先从整体分析各优化构型的s、p、d轨道，其中构型2（4）、3（4）、4（4）、4（2）的数据全为正值，说明上述构型的s、p、d轨道均净剩了自旋向上的α电子，其余构型1（4）、1（2）、2（2）、3（2）、5（2）的数据有正有负，说明其s、p、d轨道上既有自旋向上的α电子也有自旋向下的β电子。再者，比较表中数值的大小发现，相较于s、p轨道来说，9个构型都是d轨道上的成单电子最多，p轨道为次，s轨道最少。因为α电子是磁性主要贡献者，β电子对磁性有削弱作用，但二者加和发现团簇Ti3Al3二、四重态构型磁性的起到主要作用的是d轨道，其次是p轨道。在正常情况下因为电子尽可能占据能量最低的轨道，所以s层轨道都是被成对电子占据，但由表中数据可知还存在少量成单电子，据此推测可能是团簇Ti3Al3不同原子间相互影响，使得电子发生交换。

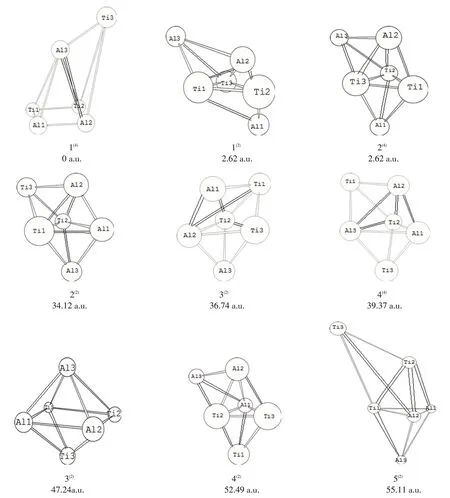
图1 团簇Ti3Al3的优化构型图

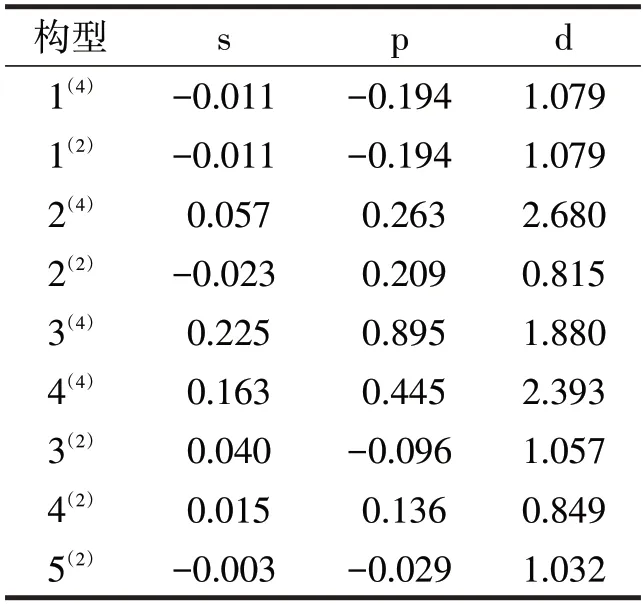
表1 团簇Ti3Al3二、四重态优化构型s、p、d轨道成单电子数

2.2.2 团簇Ti3Al3不同原子的磁矩

在铁磁金属中，由于存在交换作用的结果，参与运输的2种取向的电子在数量上是不等的。当电子数量不等即不能完全配对的时候，就会出现自旋极化。当体系有磁性并进行自旋极化计算时，可根据密里根型集聚数[13]定义磁矩：为了验证团簇Ti3A l3中不同原子对其磁性贡献的差异，通过上式计算，作出图2以对不同二、四重态构型中Ti、Al原子的磁矩进行分析比较。分析图表可以清晰地发现构型1（4）、1（2）、3（2）、5（2）中的Al原子数值为负，在构型2（4）、2（2）、3（4）、4（4）、4（2）中Al原子数值为正，但总体磁矩均为正；这就说明Al原子在团簇中有时产生削弱磁性的影响有时起到增强磁性的影响。而Ti的磁矩在所有构型中均为正，且远大于Al原子的磁矩，说明Ti原子是所有构型磁学性质的主要贡献者。再者，在构型3（4）、4（4）中Al原子的磁矩绝对值明显大于其它构型，其中构型3（4）与3（2）的差值最大，二者相差0.96μB。结合有正有负的Al原子的磁矩值能够说明，相同的原子在不同构型中对团簇的磁性产生的影响也不相同。

图2 团簇Ti3Al3二、四重态优化构型各原子的磁矩

2.2.3 团簇Ti3Al3的自旋态密度图

为了更加直观地表现各个轨道对团簇Ti3Al3磁性的贡献情况，作出如图3所示的二、四重态轨道电子自旋态密度图。图中的实线与虚线分别代表自旋向上的α电子与自旋向下的β电子在不同能量范围内的分布。磁性是由未配对的电子即净剩的α电子或净剩的β电子提供的。实线、虚线两条态密度曲线对能量的积分之和即是该轨道的成单电子数，其中自旋向上电子的态密度曲线对能量的积分为正值，反之为负值，具体数值与表3相对应。2条态密度曲线的对称性越好，则说明它们对能量的积分值就越趋向于大小相等、符号相反，则该轨道上的成单电子数越少。

如图所示，团簇Ti3Al3无论是二重态还是四重态构型，在s轨道的自旋态密度图关于横轴的对称性均较高。由此表明s轨道上净剩的成单电子较少，其对团簇Ti3Al3的磁性贡献不大。而p轨道与d轨道上电子的自旋态密度曲线则与s轨道不同，α电子态密度曲线对能量的积分值明显大于β电子态密度曲线对能量积分值的绝对值，这说明净剩自旋向上的α电子使得团簇Ti3Al3具有了磁性。d轨道的电子自旋态密度曲线是3个轨道中对称性最差的轨道，大多数构型中d轨道甚至都没有明显的最高峰，而是由多个小峰组成，这就表明d轨道上的成单电子最多，情况也最复杂，即团簇Ti3Al3的d轨道是其磁性的主要贡献者。将3组轨道整体观察，发现二、四重态构型中，不同轨道上α电子的自旋态密度最高峰均出现在p轨道电子的自旋态密度图中，说明p轨道对团簇磁性的影响同样不可忽略。

仔细观察图3发现所有构型在s轨道的0 eV处中均出现实线与虚线上下交换的情况，或者说α电子与β电子发生了转换，α电子变成了β电子自旋向下，β电子变成了α电子自旋向上。电子的自旋是粒子与生俱来的一种角动量，并且其值是量子化的，在没有外界因素干扰的前提下，无法被改变（但自旋角动量的指向可以通过干预来改变）。经过研究发现若想出现电子的自旋方向改变，它必须经过进动的过程。此处发生电子是如何产生交换作用的原因是巡游电子的磁性导致。但要说明其中的原因却不是一件容易的事情，至今仍是磁学界深入研究的重要理论课题，目前一种普遍的观点认为这和电子间的关联效应有关[15]。同一原子内3d电子自旋通过原子内交换作用相互耦合形成有序排列，它在巡游期间电子自旋的方向保持不变，这又会和另外一个原子内的3d电子自旋相互耦合而有序，于是形成铁磁性。由于这种耦合来自原子内电子之间的交换作用，所以3d金属的居里点比较高。3d电子既不像4s电子那样可以用自由电子近似来处理，也不像4f电子那样可以完全看作是局域电子，所以称之为巡游电子。

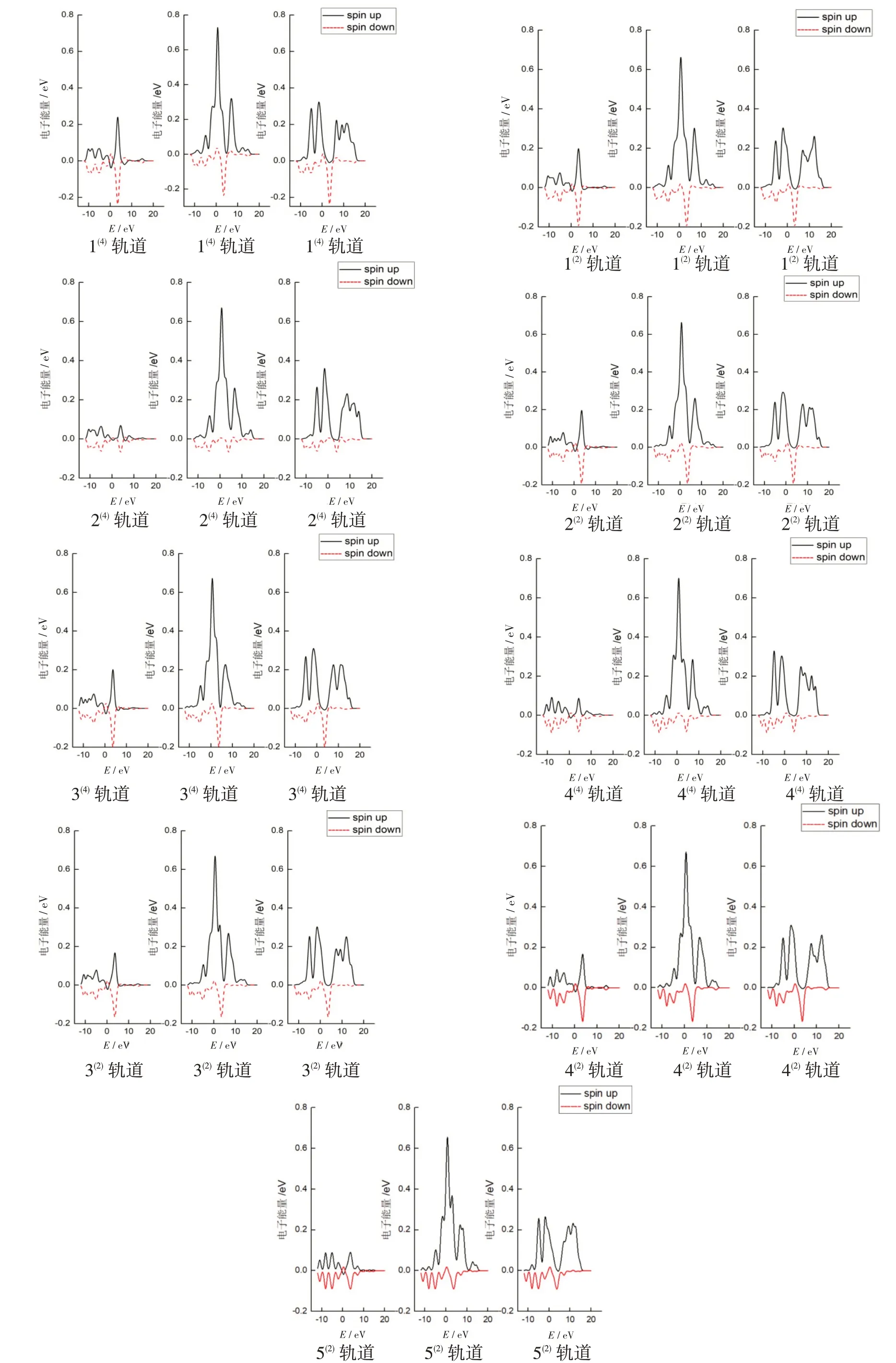
图3 团簇Ti3Al3二、四重态优化构型s、p、d轨道的自旋态密度图

3 结论

①在团簇Ti3Al3中Ti原子的磁矩对总磁矩贡献较大。②d轨道均是电子自旋态密度对称性最差的轨道，其上的成单电子最多，p轨道电子自旋态密度图的对称性稍好于d轨道，但仍有部分没有对称，由此可说明团簇Ti3Al3的d轨道是其磁性的主要贡献者，同时p轨道上的成单电子对团簇Ti3Al3磁性也有一定的贡献。③由于巡游电子的磁性导致自旋向上的α电子和自旋向下的β电子在能量值为0 eV处发生互换，且改变量完全对称。