二元函数可导性与可微性的探讨
2020-07-17王仲梅孟献青
王仲梅 ,孟献青
(1.湖南工商大学数学与统计学院,湖南长沙 410205;2.山西大同大学数学与统计学院,山西大同 037009)
1 连续、偏导数及可微的概念
定义1如果,则称函数f(x,y)在点(x0,y0)处连续。如果f(x,y)在区域D上每一点都连续,则称f(x,y)在区域D上连续。
定义2设函数z=f(x,y)在点(x0,y0)的某个邻域内有定义,如果极限存在,则称此极限为函数z=f(x,y)在点(x0,y0)处对x的偏导数,记作即类似地,函数z=f(x,y)在(x0,y0)处对y的偏导数定义为
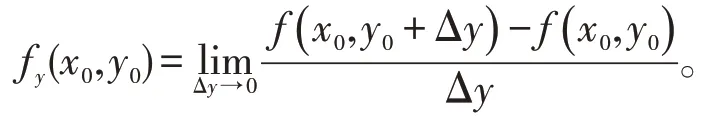
定义3如果函数z=f(x,y)在点(x,y)的全增量Δz=f(x+Δx,y+Δy)-f(x,y) 可以表示为Δz=AΔx+BΔy+o(ρ),其中,则称函数z=f(x,y)在点(x,y)可微分,AΔx+BΔy称为函数z=f(x,y)在点(x,y)的全微分,记为dz,即dz=AΔx+BΔy。
2 连续、偏导数及可微的重要定理
关于二元函数f(x,y)的连续、偏导数存在及可微已有的相关定理。
定理1若z=f(x,y) 在点(x,y) 可微分,则z=f(x,y)在(x,y)处连续。
定理2若z=f(x,y) 在点(x,y) 可微分,则z=f(x,y)在(x,y)处偏导数存在。
定理3若z=f(x,y)两个偏导数在点(x,y)处连续,则z=f(x,y)在(x,y)处可微。
定理4如果函数z=f(x,y)的两个二阶混合偏导数都在区域D内连续,则在D内,即二阶混合偏导数与求偏导的先后次序无关[1-3]。
3 连续、偏导数及可微的主要结论
结论1二元函数f(x,y)在点(x,y)的偏导数存在,但在该点可能不连续。
例1函数在点(0,0)处不连续,但偏导数在。
解故f(x,y)在点(0,0) 处极限不存在、不连续;fx(0,0)=同理,fy(0,0)=0,故f(x,y) 在点(0,0) 处偏导数存在且fx(0,0)=fy(0,0)=0。
结论2二元函数f(x,y)在点(x,y)连续、偏导数存在,但是在该点不可微。
例2函数在点(0,0) 处连续、偏导数存在且fx(0,0)=fy(0,0)=0,但f(x,y)在(0,0)不可微。
解由夹逼定理有
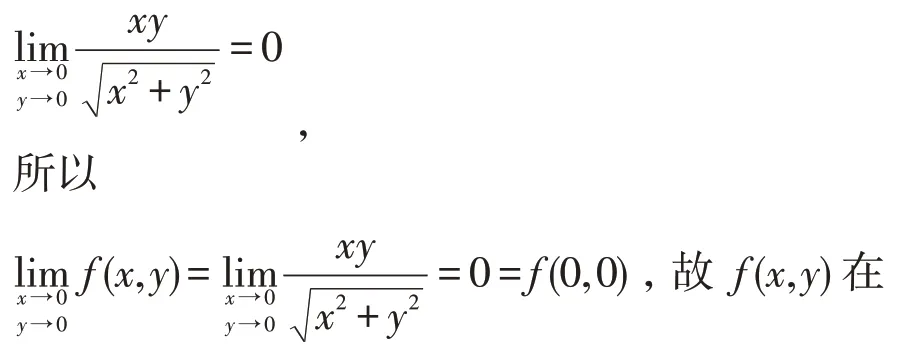
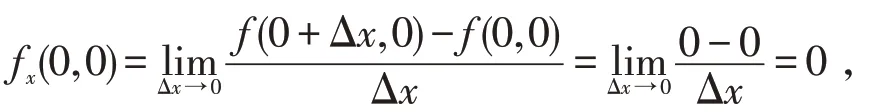
点(0,0)处连续;又同理,fy(0,0)=0,故f(x,y)在点(0,0)处偏导数存在且fx(0,0)=fy(0,0)=0;而
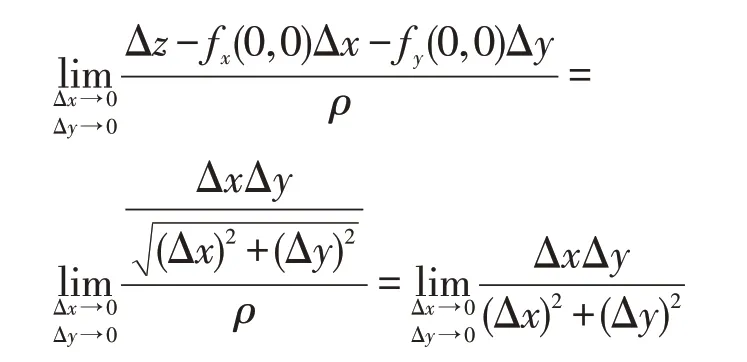
不存在,故f(x,y)在点(0,0)处不可微。
结论3二元函数f(x,y)在点(x,y)可微、但是偏导数不连续,即定理3的逆命题不成立。

例3函数在点(0,0)处连续、偏导数存在、可微,但偏导数不连续。
解故f(x,y)在点(0,0)处连续;
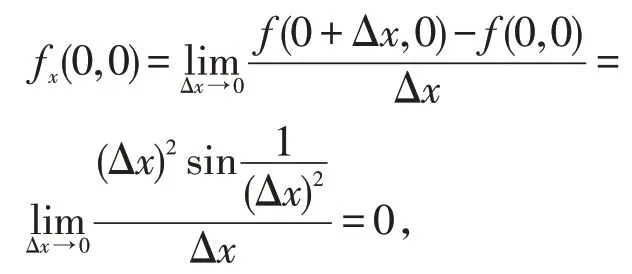
同理,fy(0,0)=0,故f(x,y)在点(0,0)处偏导数存在且fx(0,0)=fy(0,0)=0;又
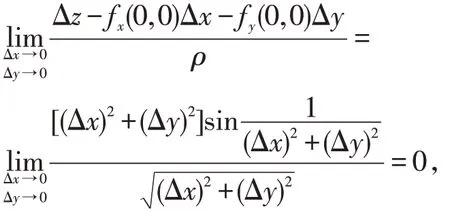
故f(x,y)在点(0,0)处可微;
当x2+y2≠0时,fx(x,y)=不存在,故不存在,所以fx(x,y)在点(0,0)处不连续。
结论4二元函数f(x,y)在点(x,y)的混合偏导数不一定相等。
例4函数fxy(0,0),fyx(0,0)存在,但是不相等。
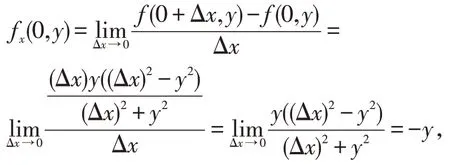
所以
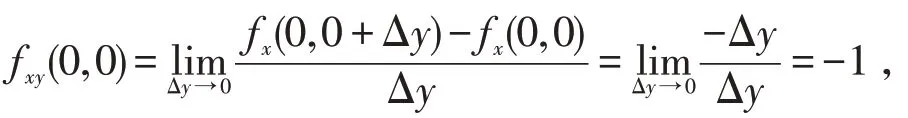
类似可得fyx(0,0)=1。
