大跨高铁梁拱组合桥轨底标高精调影响因素分析
2020-07-16徐汉斌高清炎
徐汉斌, 李 杰*, 高清炎, 贺 峥
(1.郑州大学土木工程学院,河南 郑州 450001;2.中铁十八局集团有限公司,天津 300222)
由于高速列车对运行的平稳性和舒适性要求高,因此高铁线路对线形精度要求严苛,且为了保证结构沉降稳定之后线形能够精准预测,桥梁工程成为高速铁路主要工程载体。为了满足高速铁路运行需求,一般采取跨度较小桥梁,但是由于特殊地貌、地形需要,修建大跨度桥梁不可避免,而大跨度梁拱组合体系桥在高铁桥梁选型中具有一定优势。大跨度高铁桥梁的成桥线形影响因素多而复杂,轨底标高控制为施工中主要难点。目前国内外学者主要开展了桥梁结构变形研究[1-6],如吊杆张拉和混凝土收缩徐变对结构线形影响,对于高铁桥梁轨底标高精调相关研究较少,还需进一步加强。因此,研究后期施工因素对轨底高程及轨底标高精调影响,并将实测值与理论值进行对比分析以便指导线形精调施工十分有必要。
1 工程概况
某高速铁路跨越南水北调干渠特大桥,该桥采用(74+160+74)m预应力连续梁拱组合结构形式,桥跨结构为刚性梁—柔性拱。主梁采用单箱双室变截面预应力混凝土连续箱梁,上部钢管混凝土拱肋由预制钢构件拼装成拱后泵送混凝土,采用“先梁后拱”施工顺序。拱轴线采用二次抛物线形式,拱轴线方程为y=-1/200x2+0.8x。其中计算矢高f=32 m,计算跨径L=160 m,矢跨比为1/5;横桥向设置两道拱肋,拱肋中心距为11.8 m。施工矢高f=32.12 m,拱肋实际施工均采用施工拱轴线制作和拼装。
2 建立有限元模型
采用有限元软件Midas/Civil建立该桥杆系模型,其中桥墩、主梁及拱肋采用梁单元进行模拟,拱脚采用实体单元进行模拟,吊杆采用只受拉桁架单元进行模拟。边界的模拟主要包括桥墩永久支座和0#段临时固结。按照设计图纸,每个主墩上各有3个球形钢支座,在对支座进行模拟时,在支座位置处建立上下2个节点,其中上节点与主梁刚接,下节点与主墩刚接,上下节点采用一般支承中的弹性支承进行连接,弹性连接的刚度大小由支座刚度确定。0#段临时固结采用6根钢管混凝土桩,在建立模型时,临时固结按照设计图纸建立钢管混凝土桩模型,节点与主梁采用刚性连接。全桥有限元模型共计1 733个节点和1 638个单元。
3 轨底标高精调影响因素分析
由于高速铁路运行速度较高,成桥线形会直接影响轨面标高以及行车舒适和安全性[7]。不同吊杆张拉方案、存梁时间长短、二期铺装等因素均会对成桥线形产生一定影响,不同因素对其影响也不同。本文假定结构线形变化与轨底标高直接相关。
3.1 吊杆张拉方案影响
为分析吊杆分次张拉对全桥桥面位移影响,建立两个理想状态下的模型进行对比,且张拉前存梁时间设置为3个月,两种张拉方案如下。
方案一:15组吊杆同时张拉,且初张拉每根吊杆张拉力为50 kN(约20%),二期铺装完成后,进行索力调整,一次张拉直接调整至设计张拉力大小,称为一次张拉一次调整。
方案二:15组吊杆同时张拉,且初张拉每根吊杆张拉力为50 kN(约20%),二期铺装完成后,进行索力调整,依次同时张拉至40%、60%、80%、100%(期间不考虑张拉力的损失,张拉力大小采用理论计算值),称为一次张拉分次调整。
3.1.1 梁面位移分析
仅考虑张拉吊杆引起的主梁竖向变形时,方案一和方案二主梁合计竖向位移大小如图1所示。

图1 不同张拉方案对梁面竖向位移的影响
由图1可知,对于方案一,边跨累计位移向下,最大位移处位于边跨跨中,最大位移为-0.83 mm;中跨累计位移向上,最大位移处靠近跨中,最大位移为1.62 mm。对于方案二,边跨累计位移向上,最大位移处位于边跨跨中,最大位移为11.31 mm;中跨累计位移向下,最大位移处位于中跨跨中,最大位移为-57.03 mm。由图1也可以得出,采用一次张拉一次调整方案时,梁面位移变化较小,采用一次张拉分次调整时梁面位移变化较大。
3.1.2 成桥线形分析
依据成桥分析,吊杆张拉前边跨梁面高程高于设计标高,最大高程高于设计高程20.08 mm;中跨梁面高程低于设计高程,最低高程低于设计高程47.82 mm。吊杆初张拉后,边跨梁面高程高于设计标高,最大高程高于设计高程17.43 mm;中跨梁面高程低于设计高程,最低高程低于设计高程33.59 mm。
当剩余吊杆力一次张拉调整,吊杆张拉完成后边跨梁面高程高于设计标高,最大高程高于设计高程11.51 mm;中跨梁面高程低于设计高程,最低高程低于设计高程63.43 mm。当剩余吊杆力多次张拉调整,吊杆张拉完成后边跨梁面高程高于设计标高,最大高程高于设计高程22.71 mm;中跨梁面高程低于设计高程,最低高程低于设计高程121.73 mm。吊杆张拉完成后,两种张拉方案成桥线形如图2所示。

图2 不同张拉方案对成桥线形的影响
由图2可知,两种不同张拉方案对主桥线形影响不同,且差别较大。采用方案二吊杆拉力损失较大,线形与设计线形相差较大;采用方案一吊杆张拉力损失较小,且成桥线形更接近设计线形,也更利于后期铺轨。因此,在实际施工中应优化吊杆力张拉工艺,尽可能减少张拉次数。
3.2 存梁时间对轨底线形影响
存梁时间实质是收缩徐变发生过程[8]。假设成桥1 000 d时主梁收缩徐变全部完成,某一龄期主梁关键截面梁顶面由收缩徐变引起的竖向总变形可以分为两部分:当前存梁状态下由于收缩徐变引起主梁竖向变形;当前存梁阶段已经发生的竖向变形量与成桥1 000 d竖向变形量差值,即竖向剩余变形量。
该桥设计要求成桥后存梁半年左右,然后进行轨道板等二期恒载施工;但由于工期原因,轨道板需要提前施工,这可能影响桥面最终线形进而影响铺轨。以下考虑不同存梁时间,探讨其对成桥线形的影响。
3.2.1 梁面位移分析
由于混凝土收缩徐变作用,梁面会产生竖向位移,且存梁时间不同梁面位移也不同[9]。吊杆初张拉及全桥剩余钢束张拉完成后,开始进行存梁,考虑存梁时间最大为1 a。当仅考虑收缩徐变效应对梁面位移影响时,根据计算模型可知,不同存梁时间关键截面位移变化情况见表1(“+”值表示向上位移,“-”值表示向下位移,下同)。
表1不同存梁时间关键截面梁顶面竖向位移mm

存梁时间/月边跨跨中中跨1/4截面中跨1/2截面中跨3/4截面边跨跨中10.01-0.110.80-0.110.0120.06-0.261.41-0.260.0630.14-0.421.95-0.420.1440.21-0.582.43-0.580.2150.29-0.752.88-0.750.2960.37-0.913.29-0.910.3770.52-1.234.04-1.230.5280.67-1.554.71-1.550.67120.82-1.845.33-1.840.82
由表1可知,由于中跨跨径远大于边跨跨径,故存梁时间对边跨竖向位移影响较小,对中跨竖向位移影响较大。当存梁时间为6个月时,边跨跨中竖向向上位移为0.37 mm,中跨1/4截面竖向向下位移为0.91 mm,中跨跨中竖向向上位移为3.29 mm;其余截面竖向位移关于跨中位置对称。根据计算可知,以中跨1/2截面为例,存梁第2个月主梁竖向位移相对变化量为(1.41 mm-0.80 mm)/1.41 mm=0.43,同理可得其他存梁时间下主梁关键截面梁顶面竖向位移相对变形量,不同存梁时间下主梁关键截面梁顶面竖向位移相对变形量见图3。

图3 主梁关键截面梁顶面竖向位移相对变化量
由图3可知,当存梁时间为6个月时,由收缩徐变引起主梁竖向位移相对变化量逐渐稳定且各截面相对变形量均小于22%,这与设计要求存梁时间一致,因此存梁时间为6个月的方案相对合理。但由于工期要求,实际施工中存梁时间缩短为2.5个月,由图3可知,相对于设计要求,存梁缩短为2.5个月时各截面相对变形量较大,均大于31%,此时收缩徐变对梁面位移影响较大。
3.2.2 梁面剩余变形分析
吊杆调索和二期铺装结束后,假定混凝土1 000 d完成收缩徐变。根据计算模型,当仅考虑收缩徐变效应时,关键截面梁顶面竖向剩余变形见表2。
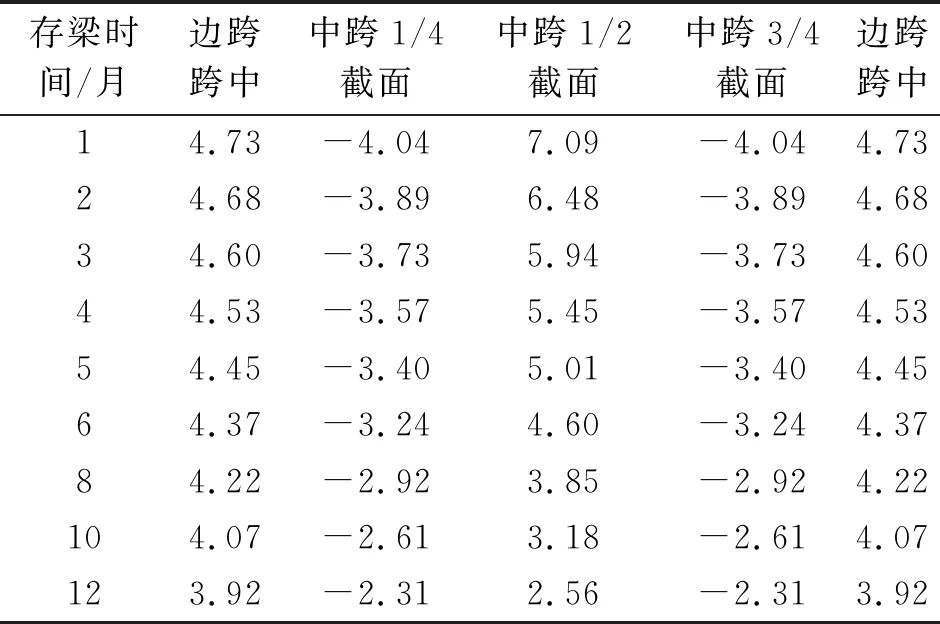
表2不同存梁时间关键截面梁顶面竖向剩余变形mm
存梁时间/月边跨跨中中跨1/4截面中跨1/2截面中跨3/4截面边跨跨中14.73-4.047.09-4.044.7324.68-3.896.48-3.894.6834.60-3.735.94-3.734.6044.53-3.575.45-3.574.5354.45-3.405.01-3.404.4564.37-3.244.60-3.244.3784.22-2.923.85-2.924.22104.07-2.613.18-2.614.07123.92-2.312.56-2.313.92
根据计算模型可知,以存梁6个月时中跨1/2截面剩余变形为基准,其存梁时间为1个月时主梁竖向剩余相对变形量为7.09 mm/4.60 mm=1.54,同理可得,当仅考虑收缩徐变效应时,关键截面梁顶面竖向相对剩余变形量见图4。

图4 主梁关键截面梁顶面竖向剩余相对变形量
由图4可知,仅考虑收缩徐变时,存梁时间对边跨剩余变形影响小,对中跨剩余变形影响大。存梁时间1个月时,边跨跨中剩余变形是存梁时间6个月时剩余变形的108.7%,中跨跨中剩余变形是存梁时间6个月剩余变形的154.0%;存梁时间3个月时,边跨跨中剩余变形是存梁时间6个月时剩余变形的105.3%,中跨跨中剩余变形是存梁时间6个月剩余变形的129.1%。存梁2.5个月时,除中跨1/2截面竖向剩余相对变形量较大,为135.0%,其余截面竖向剩余变形较小,均小于120.0%。综上所述,当存梁时间为6个月时,各截面位移相对变形量和剩余相对变形量均较小。相对变形量越小,后续轨底线形精调就越方便且越精准,存梁时间为6个月的方案相对合理。
3.3 二期恒载对轨底标高影响
施工过程中,二期恒载会使梁面产生竖向位移,由于高速铁路桥对轨面标高要求高,且一般要求在施工中不宜对轨道扣件、弹簧、垫板等进行调整(留作后期运营),施工中调整二期铺装(主要是轨道板)可改善线形以满足后期铺轨。因此,根据现场实际高程,在允许范围内调整二期铺装,使成桥时轨面高程与设计高程更为吻合。
3.3.1 二期恒载的确定
桥面二期恒载重量包括钢轨、扣件、轨道板、混凝土基座等线路设备重,以及防水层、人行道栏杆、防护墙、防抛网、电缆槽盖板及竖墙等附属设施重量。本梁为直线无声屏障,设计给出的二期恒载集度为145 kN/m,通过调整轨道板厚度改变二期恒载分析其对梁面变形影响。不同模型二期恒载集度及轨道板厚度如表3所示,其中模型四为设计值。为了简化问题,假设二期恒载引起轨道板厚度变化沿桥纵向相同。

表3 不同模型轨道板厚度及二期恒载
3.3.2 轨底标高分析
根据数值分析,不同轨道板浇筑厚度下,主梁关键截面梁顶面竖向变形见表4。
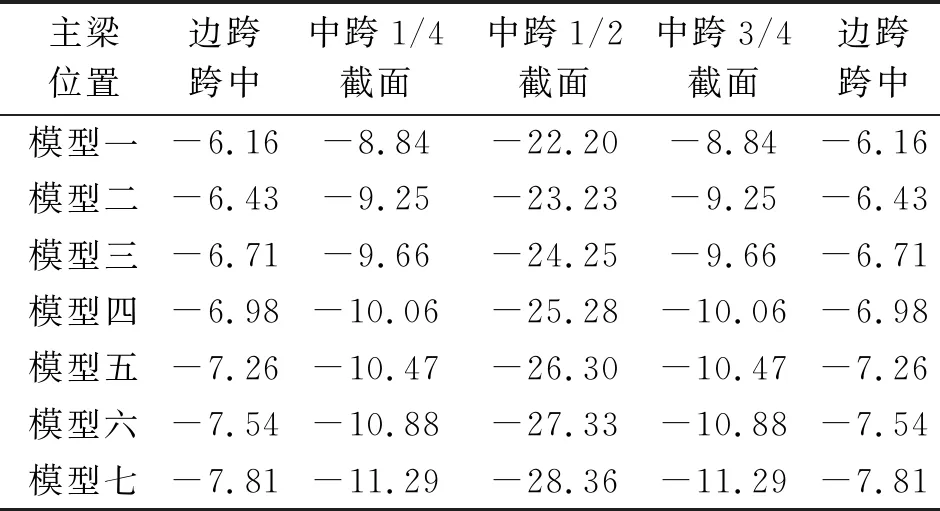
表4 二期恒载作用下主梁关键截面梁顶面轨面竖向变形mm
以轨道板厚度为500 mm对应的轨底标高为基准,即假设500 mm对应的轨底高程为0,那么以模型一为例,由于轨道板厚度不同引起相对向上变形量为25.28 mm -22.2 mm =3.08 mm,但轨道板厚度薄了60 mm,故轨底标高实际下降了56.92 mm。同理可得其余模型实际轨底标高变化量,不同轨道板厚度实际轨底标高变化见图5(以中跨1/2截面为例)。

图5 不同轨道板厚度对应中跨1/2截面实际轨底标高变化
由图5可知,轨道板浇筑厚度与轨底标高基本呈线性变化。当轨道板铺设厚度为440 mm时,中跨1/2截面对应轨底标高为-56.92 mm;当轨道板铺设厚度为480 mm时,中跨1/2截面对应轨底标高为-18.97 mm;其余截面对应轨底标高关于中跨跨中截面对称。可以看出,通过合理范围内调整轨道板厚度可以精调轨底标高。
4 现阶段轨底线形精调建议
现场实际施工过程中,主梁合龙完成后存梁2个月,随后进行拱肋拼接与吊装;待拱肋吊装完成后,在45 d内进行钢管拱混凝土灌注;之后2个月进行吊杆安装以及初张拉;2.5个月后,进行桥面轨道板以及混凝土基座的铺装;最后调整吊杆张拉力值至设计要求。在调索完成后,立即对全桥轨底高程进行了测量,轨底现阶段实测高程与设计高程差值对比情况如图6所示。

图6 轨底实测高程与设计高程差值对比
由图6可知,除边跨附近轨底实测高程高于设计高程外,其余位置轨底实测高程均略低于设计高程,最大高程差15.4 mm,位于中跨3/4截面附近,其余截面轨底高程差均小于15 mm。鉴于上述分析与实际线形,对于大桥静态验收前轨底线形精调,建议在铺设轨道板的时候,可以通过调整每段里程对应轨道板厚度,以达到所需轨底标高的精度要求。
5 结论
(1)施工过程中,不同张拉方案对主桥线形影响不同,且差别较大。当采用分次张拉时,吊杆拉力损失较大,线形与设计线形相差较大,且分次越多,吊杆拉力损失越大;但当采用一次张拉时,吊杆张拉力损失较小,且成桥线形更接近设计线形,建议施工中采用吊杆一次张拉的施工方案。
(2)由于中跨跨径远大于边跨跨径,故存梁时间对边跨竖向位移影响较小,对中跨竖向位移影响较大。但由于工期要求,实际施工中存梁时间缩短为2.5个月,此时收缩徐变对梁面位移影响相对较大,但仍处于可控范围之内,可通过最终轨底标高精调以保证顺利铺轨。
(3)仅考虑收缩徐变时,存梁时间对边跨剩余变形影响小于对中跨剩余变形影响。存梁2.5个月时,各关键截面梁顶面竖向剩余相对变形量较小,处于可控范围之内,后续施工的高铁线路轨底线形精调可通过调整轨道板或者扣件等方式进行精调。
(4)本桥除边跨附近轨底实测高程高于设计高程外,其余位置轨底实测高程均略低于设计高程,最大高程差位于中跨3/4截面处附近,最大差值为15.4 mm,桥梁静态验收前轨底标高精调可通过调整轨道板厚度实现。
