基于自由变形技术的汽车除霜风道导流板参数优化

曹斯诗，张志飞，徐中明，贺岩松，陈竹，周涛

(1.重庆大学汽车工程学院，重庆，400044；2.重庆长安跨越车辆有限公司，重庆，404000)

驾驶员快速从结霜的前挡风玻璃获得清晰的视野，对行车安全至关重要，因此，如何提高汽车除霜系统性能具有重要的实际意义。而随着计算流体力学的不断进步，数值模拟方法已成为国内外学者研究汽车除霜性能的主要手段之一。GOLDASTEH 等[1]利用k-ε湍流模型对前挡风玻璃表面风速分布进行仿真，并与实验结果进行对比，验证了仿真结果的准确性。邓峰等[2]利用半舱模型探讨了风速、湿度、温度等参数对除霜、除雾性能的影响。赵林林等[3]利用实验和数值模拟的方法，证实整车进行除霜性能稳态仿真可用半舱模型代替。李明等[4]利用k-ε湍流模型研究了出风道结构特征、出风口冲击角和温升规律对除霜效果的影响。KUMAR 等[5]优化了前挡风玻璃表面风速分布，证实了风速分布对融霜速度有较大影响。JAHANI 等[6]证实除霜风道结构对前挡风玻璃表面风速分布有较大影响。谷正气等[7]对除霜风道内的导流板进行参数优化，消除了前挡风玻璃表面的吹风死角，满足了除霜要求。虽然国内外学者对汽车除霜系统进行了大量研究，证实k-ε湍流模型能准确模拟汽车除霜性能，除霜风道结构会影响前挡风玻璃表面风速分布，从而影响除霜速度，但由于汽车除霜风道形状往往比较复杂，且不易选取参数进行优化，因此，寻求除霜风道的快速参数优化方法非常重要。自20 世纪80 年代以来，SEDERBERG 等[8]提出自由变形技术(free form deformation，FFD)，由于FFD 技术可对复杂几何进行简单、高效参数化，因而在航空、汽车等气动优化设计领域得到广泛应用。SAMAREH[9]证实了自由变形技术在气动优化中能减少参数数量，是一种有效的气动形状优化方法。LEE等[10]将FFD技术和B 样条曲面控制技术应用于3 种优化问题，发现FFD 技术更适合复杂形状的参数优化。王丹等[11]验证了FFD 技术对飞机快速参数化的应用效果，使飞机的气动阻力显著减小。汪怡平等[12-13]利用自由变形技术对汽车进行快速参数化，并建立近似模型，成功实现了汽车的气动减阻优化。考虑到自由变形技术能对复杂几何进行简单、高效的参数化的优势和除霜风道结构复杂、不易参数化的缺点，本文作者将自由变形技术应用到汽车除霜系统参数优化中。为了验证自由变形技术在汽车除霜系统优化中的可行性，以某轻型载货汽车的除霜系统作为优化对象；综合考虑该车除霜的稳态和瞬态仿真结果后，选取驾驶员侧除霜风道内的3块导流板放入晶胞型控制框架中进行参数化；利用拉丁超立方试验设计，搭建可信度高的径向基模型，最后采用遗传算法寻得导流板的最优参数，并比较优化前后的除霜性能。

1 汽车除霜性能的数值模拟

1.1 模型的建立与网格划分

图1 所示为乘员舱及玻璃分区示意图。根据GB 11555—2009[14]将图1 中的前挡风玻璃划分为A，A′和B区。

图1 乘员舱及玻璃分区示意图Fig.1 Schematic diagram of the passenger compartment and glass partition

除霜系统内气流流动复杂，因此，对除霜系统内网格进行加密处理；对空气域采用网格质量好、求解稳定性好的六面体网格，玻璃域采用四棱柱网格进行离散；近壁面采用3 层四棱柱网格，总厚度为3 mm，网格厚度增长率为1.2。求解域中截面网格划分如图2所示。网格单元数约为629万个，玻璃厚度为4 mm。

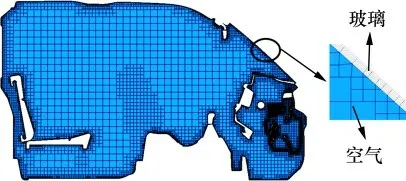
图2 求解域中截面网格划分Fig.2 Meshing of the section in the solution domain

1.2 边界条件与物理条件设置

计算域入口设置为质量流入口，流量为280 m3/h；出口设置为压力出口，为1×105Pa；空间离散格式为二阶迎风格式，计算方法为SIMPLE算法，湍流模型为Realizablek-ε模型。在瞬态计算时，除霜风道入口送风温度如图3所示；设置霜层厚度为0.44 mm，环境温度为255.13 K，设置玻璃、空气和冰层物性如表1 所示；步进为1 s，最大内部迭代为5步，计算时长为2 400 s。

1.3 初始模型除霜效果分析

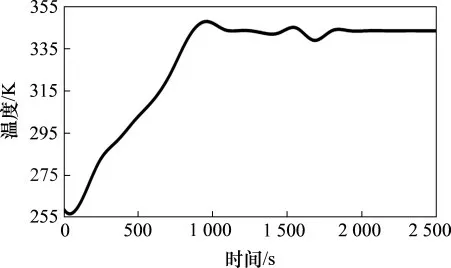
图3 送风口温升曲线Fig.3 Temperature rise curve of air inlet

表1 材料物理属性Table 1 Physical properties of materials

对该款轻型载货汽车模型进行除霜稳态分析，计算所得前挡风玻璃内表面的速度场如图4 所示。由图4 可见：在1.5 m/s 和2.0 m/s 以上风速覆盖区中，A区的覆盖面积比A′区的覆盖面积小。图5所示为不同时刻前挡风玻璃冰层厚度云图。由图5可见：融霜速度受风速分布影响较大，即A 区融霜速度比A′区的慢，且在A 区右下侧前挡风玻璃融霜速度最慢。

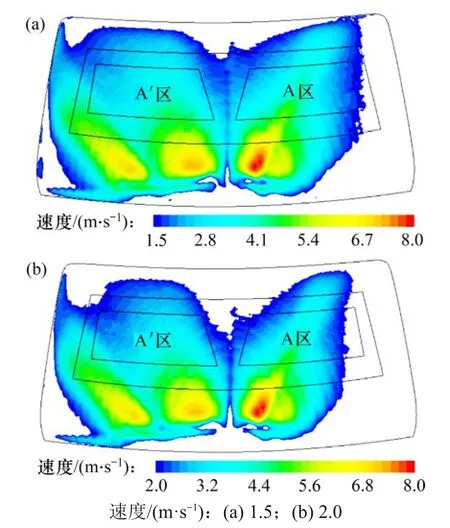
图4 挡风玻璃内表面速度分布云图Fig.4 Cloud image of velocity distribution on windshield

根据 GB 11555—2009 规定，A 区、A′区和 B区均满足除霜要求，但A′区风速分布比A 区的均匀，这使得A 区除霜速度明显比A′的区慢，且驾驶员正对A 区，使A 区遮挡驾驶员视线的时间较长，不利于行车安全。因此，有必要提高A 区除霜速度，使驾驶员快速获得清晰的视野，从而提高行车安全性。

2 基于自由变形技术的除霜优化模型

在汽车暖通系统鼓风机功率不变的情况下，A区融霜速度主要受挡风玻璃表面暖风气流分布情况的影响，而在不改变除霜风道的外形条件下，气流的分布主要由除霜风道内导流板的几何形状决定[4-7]，合理布置驾驶员侧除霜风道内的导流板几何形状对A 区的除霜性能非常重要，因此，选取驾驶员侧除霜风道内主要影响A 区流场的J1，J2和J3导流板进行变形优化，其在风道内的布置如图6所示。

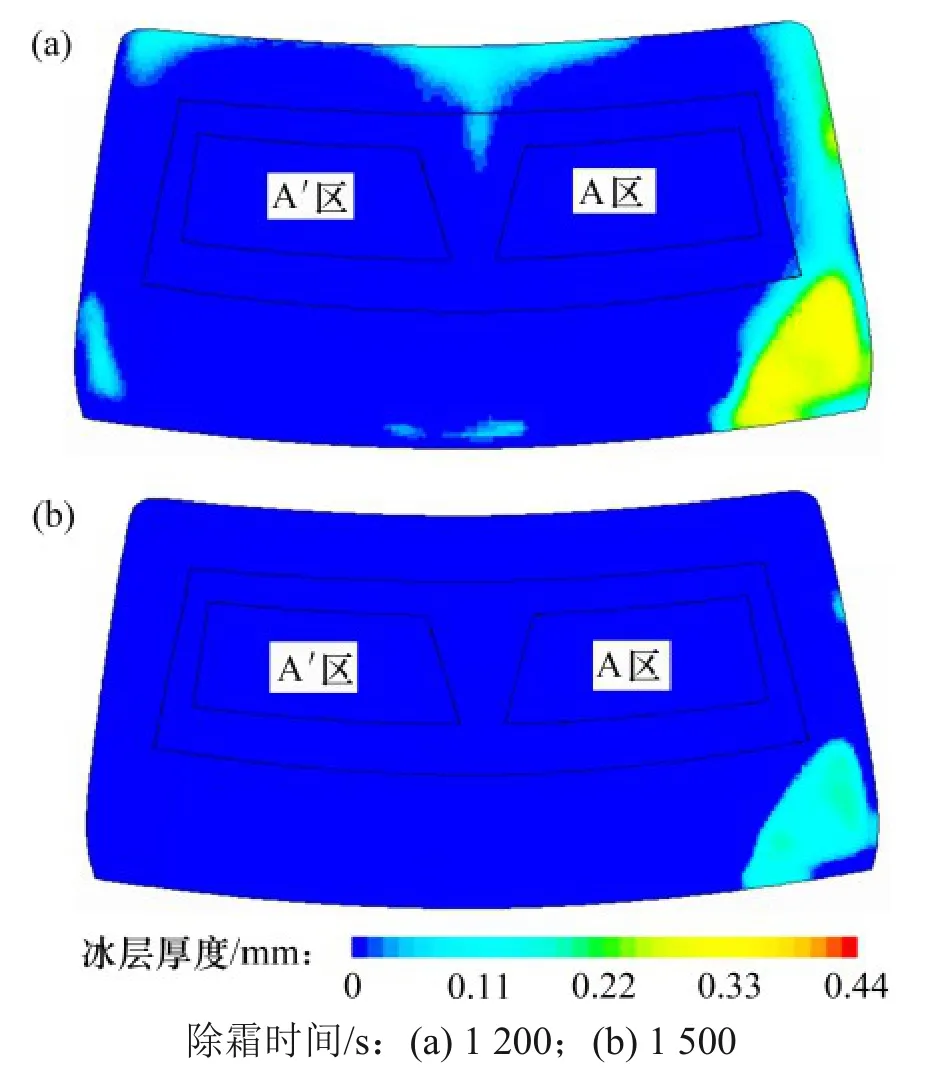
图5 不同时刻前挡风玻璃冰层厚度云图Fig.5 Cloud image of windshield’s ice thickness at different time

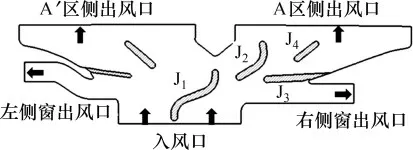
图6 除霜风道内导流板安装位置示意图Fig.6 Schematic diagram of installation position of inner deflector in defrosting duct

由于导流板J1，J2和J3几何形状较复杂，且难于多参数优化，现引进自由变形技术对导流板J1，J2和J3进行快速参数化，尽量减少参数数量。

2.1 自由变形技术

自由变形技术FFD 采用Bernstein 基函数来建立晶格控制点与晶胞型控制框架内任意点位置之间的函数关系[8]，其表达式为

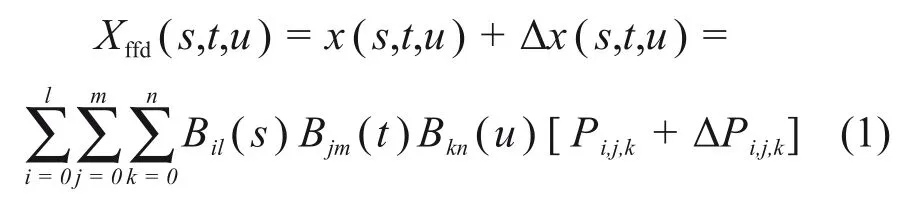
式中：(s,t,u)为晶胞型控制框架中任一点的局部坐标；Xffd(s,t,u)为对应局部坐标点(s,t,u)变形后的全局坐标；x(s,t,u)和Δx(s,t,u)为对应局部坐标点(s,t,u)的全局坐标和位移量；l，m和n为在局部坐标轴S，T和U上划分的晶格控制点数量；Pi,j,k和ΔPi,j,k为某晶格控制点变形前的全局坐标和位移。

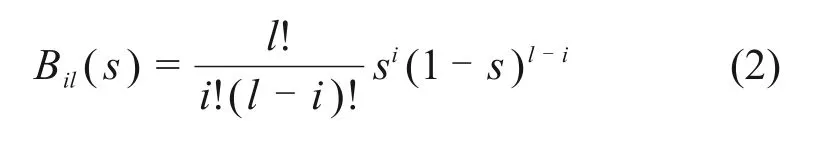
式中：Bil(s)为第i个l次Bernstein多项式基函数。

以1个半径为10 mm的球体为例，将该球体嵌入3×3×3 个晶格控制点所组成的晶胞型控制框架中，通过移动顶部中心的晶格控制点5 mm后获得如图7所示结果。该自由变形过程主要分嵌入和变形2步。

1) 将球体模型嵌入3×3×3 个晶格控制点所组成的晶胞型控制框架中，设置局部坐标系X0STU。计算球体上各点的局部坐标(s,t,u)和对应点全局坐标x(s,t,u)。

2)拖动晶胞型控制框架顶部中心晶格控制点，移动ΔP1,1,2，并通过式(1)计算球体模型变形后各点全局坐标Xffd(s,t,u)，根据球体模型变形后的全部全局坐标最终获得图7所示结果。

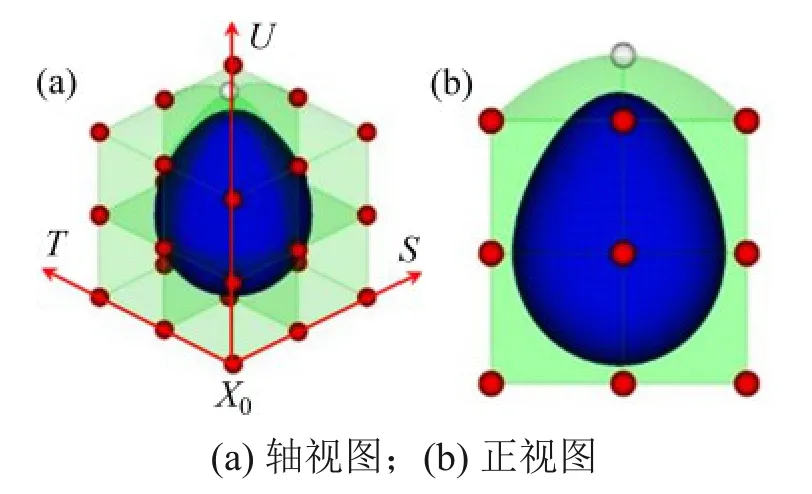
图7 球体自由变形示意图Fig.7 Schematic diagram of free deformation of sphere

2.2 设计变量与优化目标

在除霜风道中提取出导流板J1，J2和J3的几何数据，并利用FFD技术将提取的3块导流板的几何数据放入如图8所示的晶胞型控制框架中，该晶胞型控制框架为根据导流板几何形状构建的异形六面体。

如图8(b)所示，选取5个位置，以每个位置的4 个晶格控制点作为1 个变形控制点；将位置1，2，3，4 和 5 的各变形控制点坐标X1，X2，X3，X4和X5和位置点2 的变形控制点坐标Z2作为设计变量，各设计变量初始值为0，取值范围如表2所示。将剩余控制点固定不动。

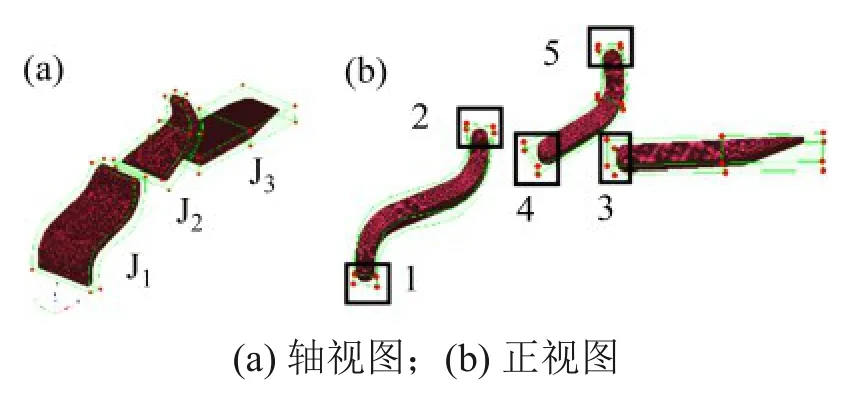
图8 导流板及晶格与参数示意图Fig.8 Deflector,lattice and parameter diagrams

表2 设计变量取值范围Table 2 Value range of design variables

由于挡风玻璃的除霜性能可由挡风玻璃表面的流场分布预测，而在工程实际应用中，可通过分析A 和A′区80%的区域是否被2.0 m/s 以上的风速覆盖以及B 区80%的区域是否被1.5 m/s 以上的风速覆盖来评估除霜性能是否达到除霜要求[15]，因此，以A和A′区表面2.0 m/s和2.5 m/s以上的风速覆盖比SA,2.0，SA,2.5，SA′,2.0和SA′,2.5与 B 区表面 1.5 m/s和2.0 m/s 以上的风速覆盖比SB,1.5和SB,2.0作为目标函数。

3 试验设计与近似模型

3.1 试验设计

考虑到设计变量和目标函数较多，在满足试验设计要求的前提下，应尽量少采样。而拉丁超立方方法可以大幅降低多因子、多水平试验设计的采样次数[12,16]，因此，选用拉丁超立方方法进行试验设计。

试验因子为变形控制点的位置参数，取值范围见表2。使用拉丁超立方设计进行42组采样，采样结果如表3 所示。根据表3，移动变形控制点的相应位置，获得42组导流板几何数据。

考虑到乘员舱(全舱模型)体积较大，且全舱模型后部回流的气流对前挡风玻璃内表面的流场分布影响甚微，且截取B 柱前部的乘员舱模型(半舱模型)和全舱模型的除霜稳态结果几乎一致[3]，因此，为节省计算时间，将该乘员舱从B 柱中间截断，保留B柱前部的半舱模型，如图9所示，并将变形后的导流板J1，J2和J3的几何数据导入半舱模型中进行数值计算，获得如图10所示的42组目标函数值。

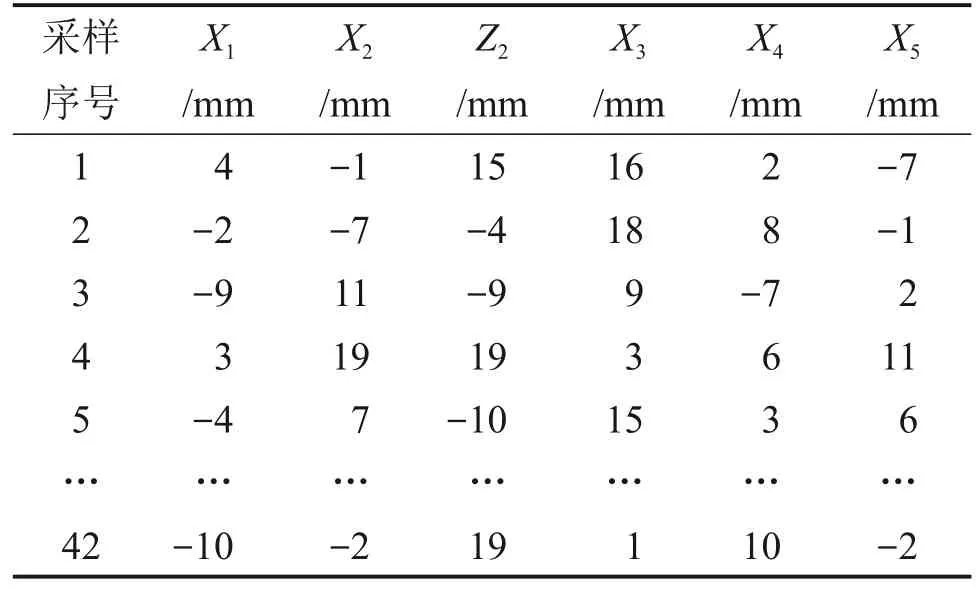
表3 试验设计结果Table 3 Test design results

3.2 近似模型的建立与检验

由于设计变量和目标函数较多，采样数据较少，近似模型关系较复杂。径向基模型(radial basis function，RBF)是一种神经网络模型，能很好地逼近复杂非线性函数，在同等条件下，尤其适用于较少样本点的情况，具有近似模型质量好、拟合速度快和精度高等优点[17]，因此，选用RBF模型作为导流板优化的近似模型。

为检验RBF 模型拟合精度，借助决定系数R2进行评估，R2越大，拟合精度越高[13]。经过计算，RBF 模型的R2=1，拟合精度满足要求(R2＞0.9)。为更直观地检验RBF 模型的拟合精度，另外选取除42组采样点外的3组新采样点作为检验点，3组检验点集如表4所示。根据3组检验点对导流板进行自由变形，并将变形后的导流板几何数据导入半舱模型中进行数值模拟，得到的仿真结果与RBF模型中对应的结果进行比较，对比结果如表5 所示。由表5 可知：3 组检验点的仿真结果与对应RBF 模型结果的相对误差均在±5%以内，拟合精度高，因此，选择RBF 模型可以作为导流板优化的近似模型。

3.3 近似模型的求解

除霜性能的优化目标是在保证A′区除霜效果的同时，提高A区和B区的除霜效果，属于典型的多目标优化问题[18]。针对多目标问题，通常是将其转化为单目标问题进行寻优[19]，因此，设定单目标函数Fmax为

图9 半舱模型示意图Fig.9 Diagram of half passenger compartment model

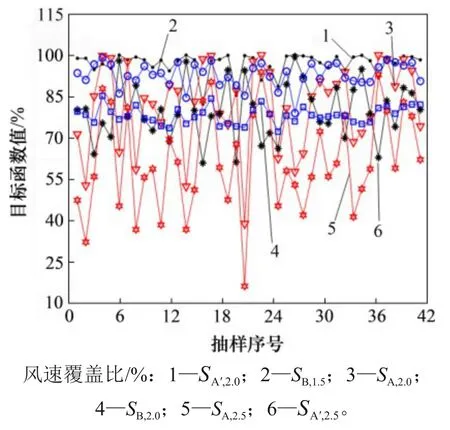
图10 采样点目标函数值Fig.10 Objective function value of sample point

表4 检验点集Table 4 Checkpoint set

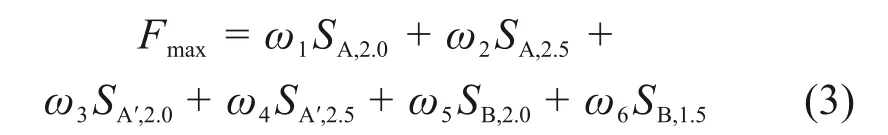
式中：ω1，ω2，ω3，ω4，ω5和ω6为权重系数；0.8＜SA,2.0＜1.0，0.8＜SA′,2.0＜1.0，0.8＜SB,1.5＜1.0。 根 据GB 11555—2009 规定，检验 A 区、A'区和 B 区满足除霜性能要求的时间分别为20，25 和40 min，且各区表面各风速对除霜均有效果，因此，根据1 h 内各区除霜速度，令权重系数分别为0.21，0.21，0.18，0.18，0.11和0.11。

由于遗传算法为群体搜索，利于搜出全局最优，且效率高[7]，因此，利用遗传算法在建立的RBF 模型上进行全局寻优。为了得到准确的优化结果，将遗传算法的初始种群数G按式(4)计算并设为106 个，最大内部迭代为50 步，最小内部迭代为25步，突变率为0.01。

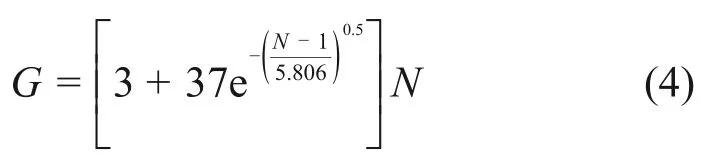
式中：N为设计变量个数。

最终设计变量优化结果如表6所示。按优化后的设计参数对导流板进行自由变形，并与初始导流板J1，J2和J3进行对比，变形前后导流板对比示意图如图11 所示。由图11 可知：优化后的导流板J1和J2较平顺，弯曲弧度没初始的大；导流板J1较初始的长，而导流板J3较初始的短。3块导流板之间的最小间距增大。

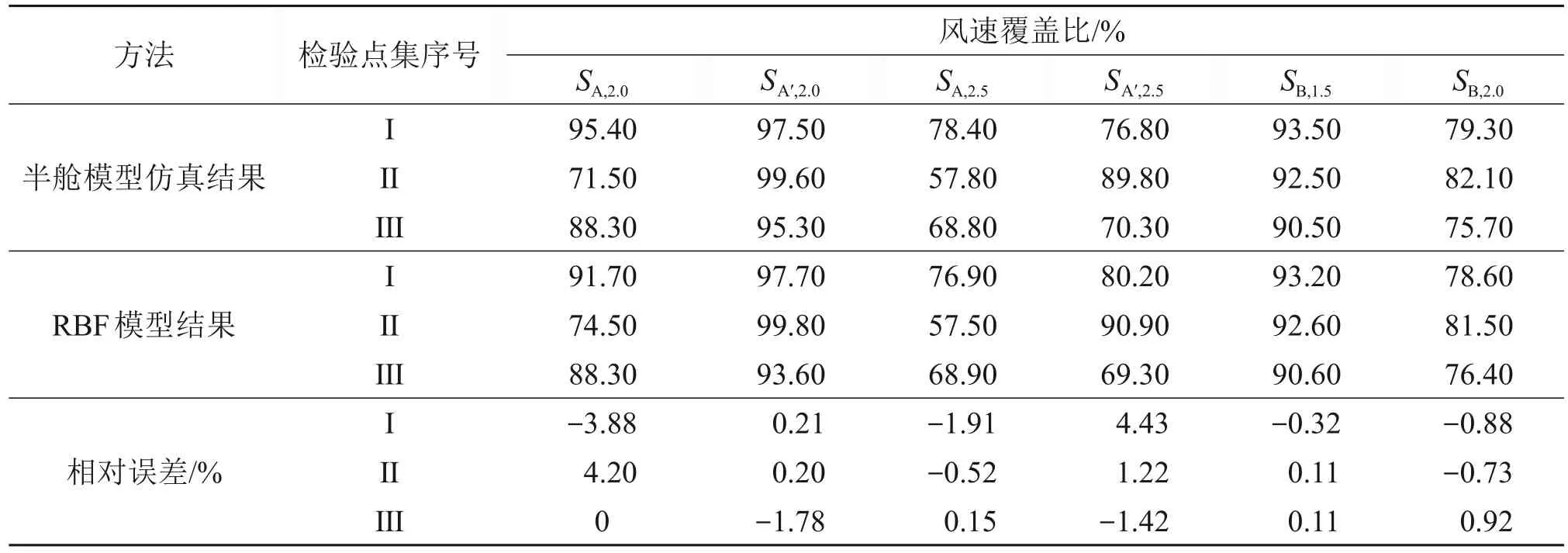
表5 RBF模型精度检验Table 5 Accuracy test of RBF model

表6 设计变量优化结果Table 6 Optimization results of the designed variables

图11 变形前后导流板示意图Fig.11 Schematic diagrams of the deflector before and after deformation

将优化后的导流板J1，J2和J3的几何数据导入半舱模型中进行数值模拟。将得到的半舱模型仿真结果与RBF 模型中对应的寻优结果进行比较，如表7所示。由表7可知：A区表面2.5 m/s以上风速覆盖比的相对误差最大，为-5.98%，其余区域风速覆盖比的相对误差均在±3%以内，说明所建RBF近似模型可信度高。

表7 风速覆盖比仿真与寻优结果对比分析Table 7 Comparison and analysis of simulation and optimization results of wind speed coverage ratios

4 除霜效果分析

将优化后的导流板J1，J2和J3的几何数据导入全舱模型中进行数值模拟，并与半舱模型的数值模拟结果进行对比，如表8所示。由表8可知：半舱模型与全舱模型数值模拟结果相似，误差均在±5%以内，进一步说明对体积较大的乘员舱进行优化研究时，可用半舱模型进行研究。

表8 半舱和乘员舱模型各区风速覆盖比Table 8 Wind speed coverage ratios in each section of the model of half cabin and crew cabin

4.1 稳态结果分析

为了更直观地说明优化后模型的风速分布情况，将优化后的全舱模型与初始的全舱模型进行对比。图12 所示为除霜风道内流线图，表9 所示为优化前后各区风速覆盖比。由图12和表9可知：

1)由于优化后的导流板J1被拉长，阻碍了除霜风道内驾驶员侧气流流向副驾驶员侧，使A′区2.0 m/s 和2.5 m/s 以上风速覆盖比从初始的99.63%和90.41%分别下降到99.47%和86.96%；

2)与初始导流板J2相比，优化后的导流板J2弯曲弧度减小，更平滑。流经导流板J2附近区域的气流更顺畅、发散，使A 区2.0 m/s 和2.5 m/s 以上风速覆盖比从初始的82.79%和64.09%提升到99.34%和86.91%，提升比例均在19%以上。

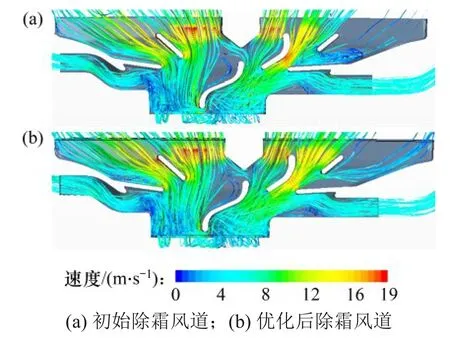
图12 除霜风道内流线图Fig.12 Internal flow diagram of defrosting duct

表9 优化前后各区风速覆盖比Table 9 Wind speed coverage ratios of each district before and after optimization

3) 优化后的导流板J3更短，且在导流板J3上部，靠近前挡风玻璃侧，无涡流作用，使气流流动更顺畅；而且导流板J3与上部导流板J2和J4协同作用，加速气流流动。这使B 区的1.5 m/s 和2.0 m/s 风速覆盖比均提升4.5%以上，从初始的93.98%和79.11%提升到98.48%和84.81%。

4.2 瞬态结果分析

图13 所示为前挡风玻璃不同时刻各区域除霜覆盖比，由图13 可见：由于优化后的A′区表面各风速覆盖比相比初始模型的略有下降，但A区和B区表面风速分布得到明显改善，增强了A区和B区的对流换热能力，使A 区除霜面积达到80%和100%的时间分别比初始模型提前17 s和40 s；B区除霜面积达到95%的时间比初始模型提前6 s；而A′区除霜面积达到80%和100%的时间仅比原模型分别延后了5 s和7 s。对比结果表明，优化后前挡风玻璃表面的除霜总时间缩短，前挡风玻璃A 区融霜速度比A′区的快。因此，对除霜风道内的导流板进行优化，能有效提高汽车的除霜性能。

图13 前挡风玻璃不同时刻各区域除霜覆盖比Fig.13 Defrosting coverage ratio of each area in front windshield at different time

5 结论

1)对某轻型载货汽车除霜系统进行数值模拟，发现A 区表面流场分布没有A′区的均匀。为此，本文作者以除霜风道内的3 块导流板为优化对象，利用自由变形技术对其进行快速参数化，减少了优化的参数数量。

2)通过抽样的方法搭建了高精度的近似模型，并利用遗传算法寻优得到了最优结果。优化后A区2.0 m/s 和2.5 m/s 以上风速覆盖比均提高19%以上，A区除霜面积达到80%和100%的时间分别提前 17 s 和 40 s；使 B 区 1.5 m/s 和 2.0 m/s 风速覆盖比均提升4.5%以上，B 区除霜面积达到95%的时间提前6 s，有效改善了前挡风玻璃表面风速分布和对流换热能力。

3)自由变形技术能简单、高效地对除霜风道内复杂形状的导流板进行快速参数化，有效改善汽车除霜系统性能。