改进的属性区间识别方法及其在隧道突涌水风险评估中的应用

2020-07-16周宗青孔军杨为民陈元培张琦李利平石少帅

中南大学学报(自然科学版) 2020年6期

周宗青，孔军，杨为民，陈元培，张琦,3,4，李利平，石少帅

(1.山东大学齐鲁交通学院，山东济南，250002；2.齐鲁交通发展集团有限公司，山东济南，250101；3.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京，210098；4.山东省高速公路技术和安全评估省级重点实验室，山东济南，250002)

突水、涌泥灾害已成为国内外学者及现场技术人员重点关注的地质灾害之一[1-2]。人们采用应用属性识别理论[3]、模糊综合评价法[4]、层次分析法[4-5]、神经网络法[6-7]、加权平均法[8]、可拓理论[9]、灰色聚类[10-11]等方法，对隧道突水、涌泥危险性进行了分析和评价，并建立了相应的评价模型与评判标准。李利平等[11-12]对岩溶隧道及深埋长隧道突水灾害的主要影响因素进行了分析，构建了评价指标体系及动态评价系统。然而，模糊综合评价法因隶属函数的构建问题，取值运算时会舍去大量中间值信息，从而导致分类不明确、结果不合理等问题；而神经网络模型不仅需要人为设计网络参数，还要通过多次迭代才能得到较理想的结果[13]。程乾生[14]提出了属性识别理论模型，重点讨论了定性描述的度量问题，有效解决了有序分割问题。而隧道突水、涌泥风险评价问题可归结为对定性描述的度量问题，因此，属性识别理论为解决该问题提供了理论基础。周宗青等[2]应用属性识别理论对岩溶隧道突水风险进行了评价与识别，发现理论结果与现场结果一致，验证了其应用于突水、涌泥风险评价的可能性。此外，属性识别理论模型也已成功应用于其他领域。吴毅江等[15]应用属性识别模型，对山坡稳定性进行了评价；LI等[16]将属性数学理论与层次分析法相结合，应用于煤层底板突水风险评价；文畅平等[17-19]应用属性综合评价系统对煤层瓦斯突出等多个工程问题进行研究，均证明该方法理论评价结果是合理且可行的。然而，采用上述方法对灾害进行风险评价时，其评价指标仅仅取1个固定值，未考虑到工程地质条件存在的复杂性以及灾害风险的不确定性。李群等[20]构建了属性区间识别模型，将评价指标的等级划分标准拆为2个标准，但其评价指标仍是1个值，并未将评价指标扩展为一个小范围区间。李术才等[21-22]初次将评价指标扩展为一个小范围区间，并将属性区间识别理论应用于突水、岩爆、底板透水、瓦斯突出等灾害风险评价中，使得风险评价上升到了定量阶段。本文作者基于文献[20-21]中的评价方法，提出一种新的属性区间识别方法，并将其应用到岩溶隧道突涌水风险评价中；通过与其他评价方法进行对比，验证本文方法的可行性与有效性。

1 改进的属性区间识别方法

1.1 单指标属性测度分析

设评价对象有m个评价指标Ij(j=1，2，…，m)，对于每个评价对象都有K个评价等级Ck(k=1，2，…，K)。考虑地质条件复杂性和不确定性，实际工程中第j个评价指标的取值范围为[tjx，tjy]，其单指标属性测度通过构建属性测度函数来计算，用一个属性测度区间[μjk]=[-μjk，μˉjk]来表示。采用属性识别模型中的属性测度函数构建方法[20]，将其风险评价指标的等级划分标准(见表1，ajk和bjk分别为第j个评价指标的第k个评价等级对应的指标取值范围的下限值和上限值)用2个矩阵来表示，如式(1)～(2)所示。

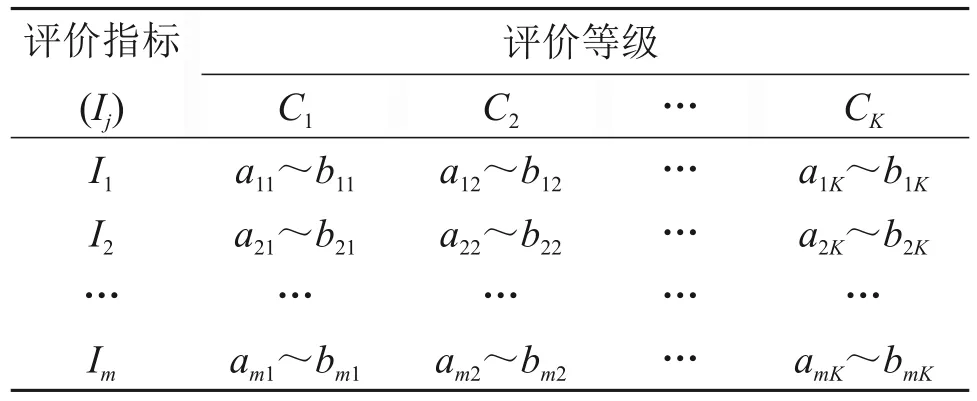
表1 评价指标等级划分标准Table 1 Classification criteria of evaluation indices grades

式中：ajk＜bjk并满足aj1＜aj2＜…＜ajK，bj1＜bj2＜…＜bjK；或者ajk≥bjk并满足aj1＞aj2＞…＞ajK，bj1＞bj2＞…＞bjK。

当ajk＜bjk且aj1＜aj2＜…＜ajK，bj1＜bj2＜…＜bjK时，单指标属性测度计算方法如下(计算时tj分别取指标取值范围的下限tjx和上限tjy进行计算)：

当tj≤aj1时，取

当tj≤bj1时，取

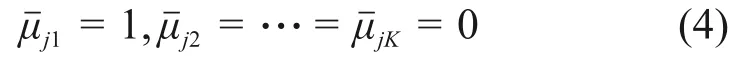
当tj≥ajK时，取

当tj≥bjK时，取

当ajk≤tj≤ajk+1时，取

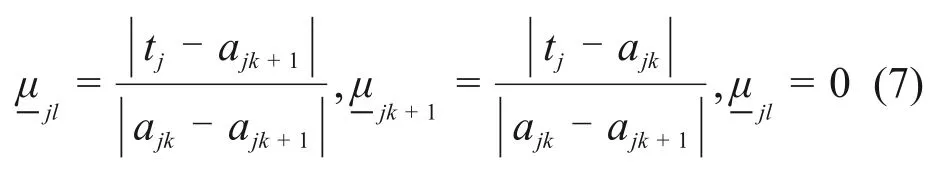
式中：l＜k或l＞k+1。

当bjk≤tj≤bjk+1时，取

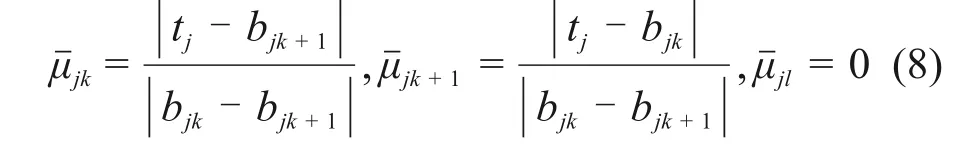
式中：l＜k或l＞k+1。

对于tjx，计算后可得到2 个单指标属性测度矩阵：

对于tjy，计算后同样可得到2个单指标属性测度矩阵，形式与式(9)和(10)相同。

1.2 多指标综合属性测度分析

对于式(3)～(8)计算得到的单指标属性测度矩阵，相对应地可以得到4个综合属性测度，计算式如下：

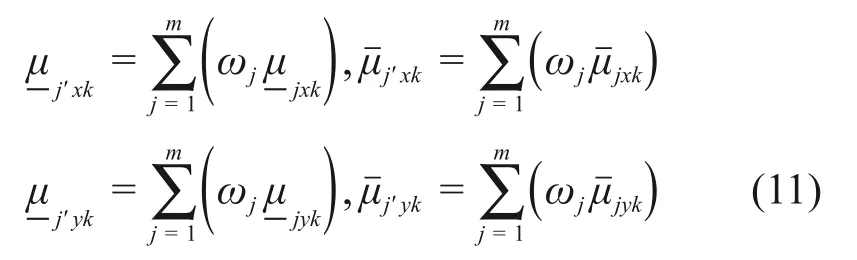
式中：ωj为第j个评价指标的权重，满足

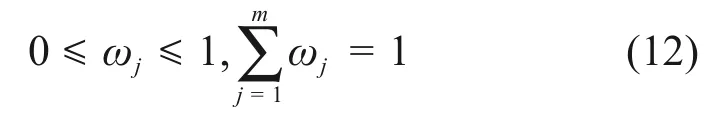
1.3 属性识别分析

属性识别分析采用置信度准则，置信度系数λ一般取0.6～0.7[14]。

当C1＞C2＞…＞CK时(C1为微危险性对应的评价等级，C2为低危险性对应的评价等级，…，CK-1为中危险性对应的评价等级，CK为高危险性对应的评价等级)，即C1优于C2，C2优于C3，…，CK-1优于CK时，若满足：

则认为评价对象属于Ck0级别。

当C1＜C2＜…＜CK时(C1为高危险性对应的评价等级，C2为中危险性对应的评价等级，…，CK-1为低危险性对应的评价等级，CK为微危险性对应的评价等级)，即CK优于CK-1，…，C3优于C2，C2优于C1时，若满足：

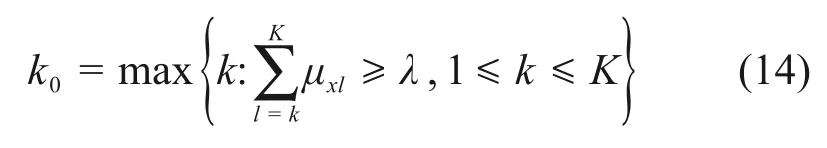
则认为评价对象属于Ck0级别。

本文作者基于式(11)计算得到的综合属性测度，提出一种改进的属性识别方法。

1.3.1 定性分析

首先，计算第k个评价等级对应的综合属性测度平均值μk：

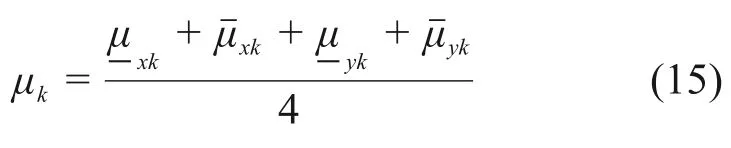
然后，基于式(15)计算得到的μk，根据置信度准则判别评价对象的风险。

1.3.2 概率分析

定义向量：

此时，式(9)～(10)可表示为

测量上限tjy对应的单指标属性测度矩阵可表示为

从而得到2个单指标属性测度矩阵：

式中：

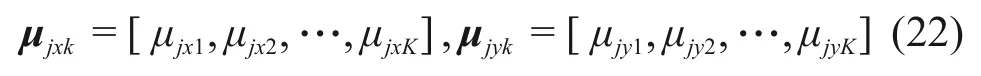
将μjxk和μjyk按序排列组合构建1个m×K阶矩阵Ujk(即指评价对象第j个指标的单指标属性测度组成的向量作为Ujk的第j行)，通过上述方法构建可以得到2m个Ujk。

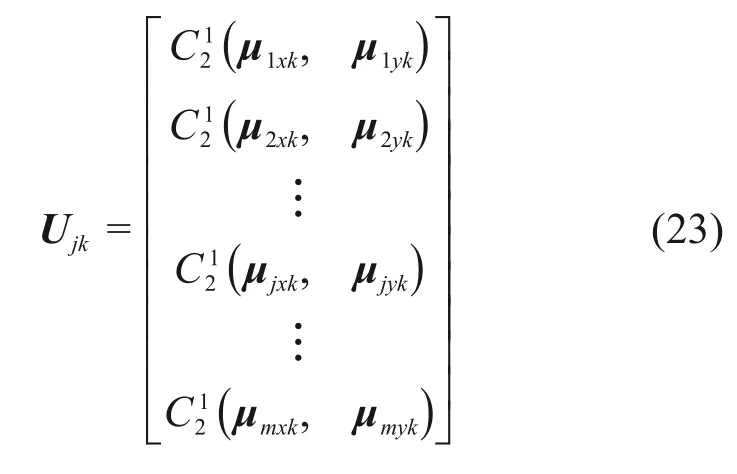
Ujk可以表示如下：

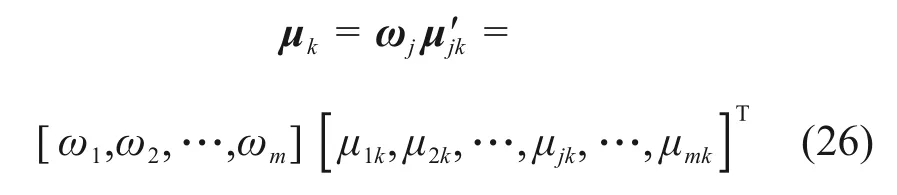
式中：ωj为评价指标的权向量。

最后，针对计算得到的每1 个Ujk，采用置信度准则进行风险等级评判。每1个Ujk都对应着1个风险等级Ck0，同理可得到2m个k0；然后，统计k0分别取1，2，…，K时各有多少种情况，并计算其所占的比例。

2 岩溶突水风险属性区间识别模型

2.1 风险评价指标

参照文献[2,21]中的评价指标及分级标准，通过属性测度的分析，对其分级标准上下限进行量化设定，转化为有限区间，见表2。

2.2 属性测度函数

根据表2 中的评价指标分级标准以及式(3)～(8)，构造属性测度函数，如图1所示。其中，评价指标I1分为岩层可溶性与专家评分2 种标准。I1，I2，I6和I7专家评分的属性测度函数一致(见图1(a))。

2.3 指标权重分析

选用主观客观综合赋权法，该方法结合了频数统计法与层次分析法，不仅可参考专家意见，避免过于依赖统计或数学定量方法，同时可根据现实情况调整各评价指标，尽量避免主观随意性。

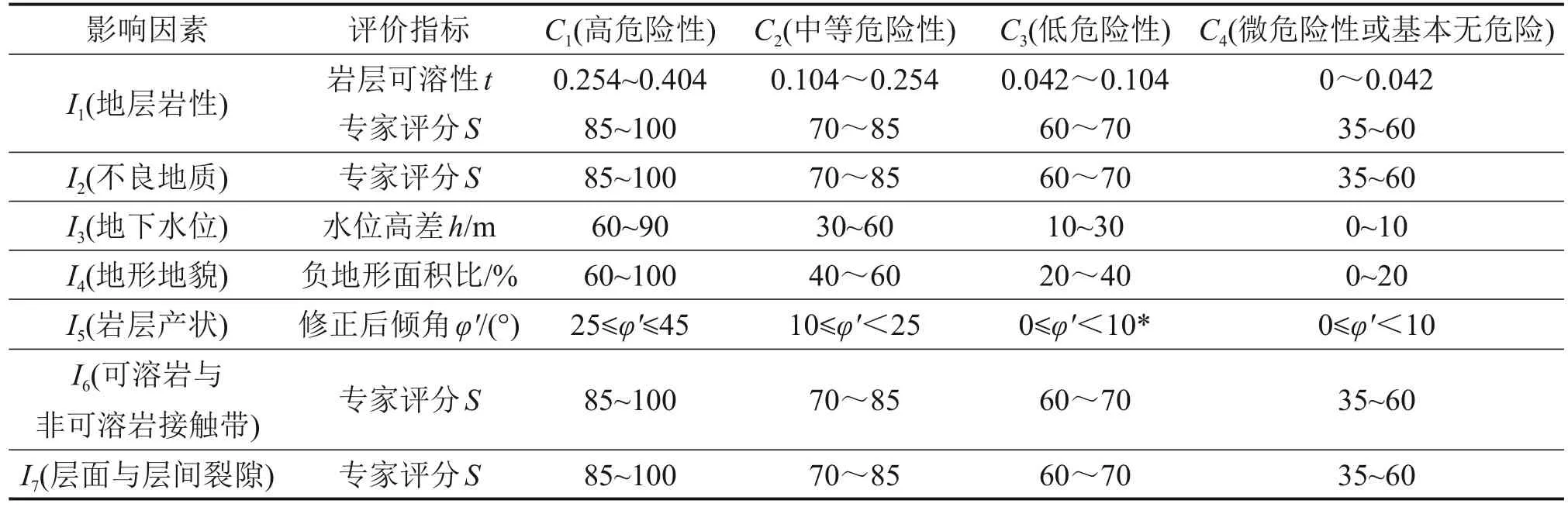
表2 突水风险评价指标及分级标准[21]Table 2 Indices and criteria for risk assessment of water inrush[21]

图1 突涌水风险评价指标属性测度函数Fig.1 Single attribute mathematical functions of risk indices of water inrush

式中：ωj1为客观权向量；ωj2为主观权向量；ψ1为客观权重的权值；ψ2为主观权重的权值。

参考文献[21]，进行权向量取值：

主、客观权值均取0.5，则综合权向量ωj为

3 工程应用与验证

3.1 鸡公岭隧道突涌水灾害风险评价

结合文献[21]中的属性识别分析案例，对三峡翻坝高速公路鸡公岭隧道ZK19+509—ZK19+539段突涌水灾害风险进行评估，其评价指标的取值区间见表3。

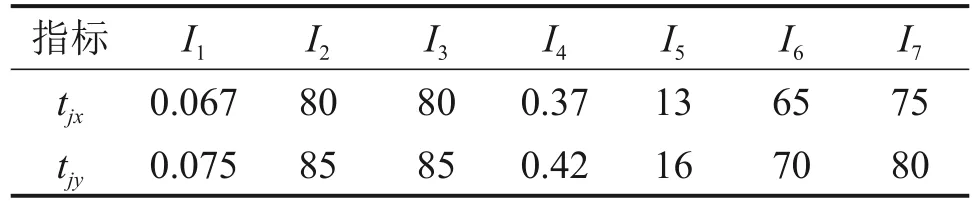
表3 评价指标取值区间[21]Table 3 Value ranges of evaluation indices[21]

根据图1 构建的属性测度函数，对表3 中的tjx和tjy进行相应的属性测度计算，得到单属性测度矩阵：

应用本文第1.2 节方法进行综合属性测度分析，采用定性与概率分析2种方法对案例1进行分析对比。

3.1.1 定性分析

由式(11)求得μk属性测度：

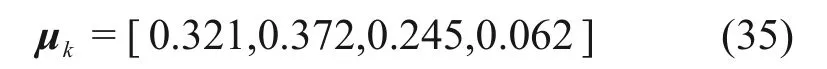
进行风险等级评估时，置信度系数λ取0.65，根据式(13)和(14)可得k0=2，即说明该段隧道突水风险等级属于C2级。

3.1.2 概率分析

由式(20)得到矩阵Ujxk与Ujyk，通过μjxk和μjyk排列组合，得到27种组合，即128个Ujk。针对计算得到的每一个Ujk，采用置信度准则进行风险等级评判。

分析结果表明：在Ujxk与Ujyk的128种有序组合中，有20种组合k0=1，对应风险为C1级；有84种情况k0=2，对应风险等级为C2级；有24 种组合计算结果在0.345～0.355 之间，难以准确对其进行归类。可认为该段隧道段可能发生C1级突水概率为15.625%，发生C2级突水的概率为65.625%，另有18.750%的危险性介于C1～C2级之间。

图2 所示为风险评价结果对比。由图2 可知：采用本文定性分析方法，认为该段突涌水风险等级为C2级；采用本文概率分析方法，认为该段大概率发生C2级突涌水，小概率发生C1级突涌水，仅有18.750%的概率发生C1～C2级突涌水(分类模糊)；根据文献[21]，该段发生C2级突涌水风险的概率为50%，另有50%的概率发生C1～C2级突涌水，也就是50%的结果出现了分类模糊或分类不清的现象。对比可知，与文献[21]中方法相比，本文所述概率分析方法所得的结果中分类模糊的情况更少，评估结果更明确。

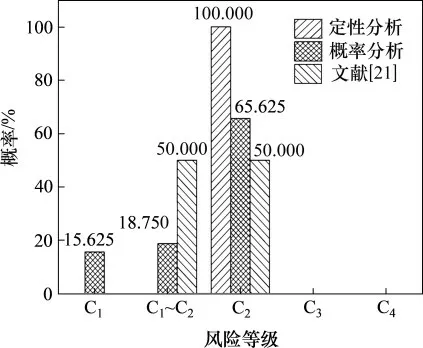
图2 风险评价结果对比Fig.2 Results comparison of risk assessment

3.2 峡口隧道突涌水风险评估验证

3.2.1 评价指标取值区间

结合文献[21]中的工程案例，选取峡口隧道XJK0+060—XJK0+110段，进行突水危险性等级评价。评价指标取值区间如表4所示。

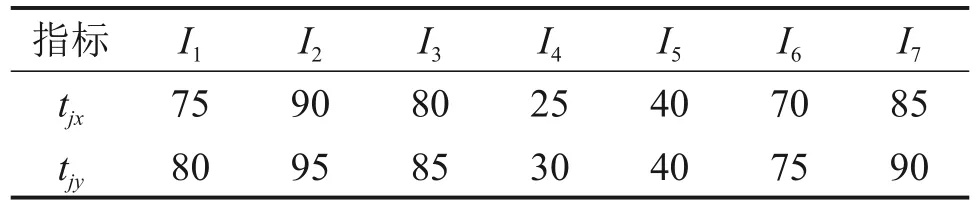
表4 XJK0+110～XJK0+060段评价指标取值区间[21]Table 4 Value intervals of evaluating indices for XJK0+110～XJK0+060[21]

3.2.2 突水风险属性识别分析

根据本文第1.2节，对表4中tjx和tjy进行属性测度计算，计算结果以矩阵表示，如式(37)～(40)所示。

1)定性分析。采用定性分析，可计算得到综合属性测度μk：

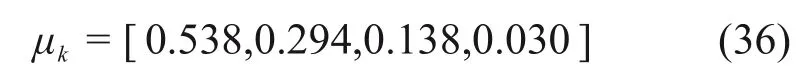
根据置信度准则见(式(13)和(14))计算，取λ=0.65，可知k0=1。

2)概率分析。通过μjxk和μjyk排列组合，各组矩阵组合结果均为k0=1，说明该隧道发生C1级突水的概率为100%。

李术才等[21]运用属性区间评价理论对该工程案例的评价结果均为C1级，与本文改进属性区间识别理论的评价结果一致，且在实际工程开挖过程中，在掌子面XJK0+101，XJK0+093，XJK0+087—XJK0+063 和 XJK0+095—XJK0+080 段均发生重大突涌水灾害，验证了评价结果的准确性。