地铁车轮凹陷磨耗对踏面接触应力的影响

周志军，李伟，陈斌，温泽峰

(西南交通大学牵引动力国家重点实验室，四川成都，610031)

地铁车辆在运行过程中受线路条件、轮轨参数匹配、运行速度和频繁牵引制动等因素的影响，车轮踏面不可避免地发生磨耗和疲劳损伤等现象。车轮凹陷磨耗是典型的踏面磨耗现象，表现为轮缘磨耗轻微，名义滚动圆附近磨耗严重，两侧磨耗量逐次递减。车轮出现凹陷磨耗后，轮轨接触区域产生强非线性接触特性，轮轨相互作用关系恶化。车轮踏面在长期反复滚动接触载荷作用下，会产生局部永久性累积损伤，导致接触表面产生剥离等疲劳损伤现象，影响列车安全运行。国内外学者针对车轮凹陷磨耗和踏面剥离损伤现象，结合现场试验和数值仿真法展开了研究。SAWLEY 等[1]调查发现北美货车6 700 个车轮踏面廓形中21%的车轮凹陷磨耗量大于2 mm，模拟结果表明，当凹陷磨耗量大于2 mm时，轮轨滚动阻力增加，轮轨接触应力明显增加。黄照伟等[2]的研究表明当高速列车凹陷磨耗车轮与标准钢轨匹配时，在多个平衡位置间跳跃造成“轮缘到假轮缘”的冲击振动，影响车辆运行性能。孙宇等[3]基于传统的Kik-Piotrowski方法，考虑轮对摇头和多点接触问题，仿真分析了具有磨耗车轮的轮轨动力相互作用关系，发现车轮凹陷磨耗会增加轮轨高频垂向振动，使轮轨横向力的振动幅值显著增加，影响行车平稳性和安全性。陶功权等[4-5]基于车辆系统动力学仿真模型，建立了考虑安定图和损伤函数的车轮滚动接触疲劳分析模型，研究了车辆通过3种不同半径曲线时轮轨磨耗状态对车轮滚动接触疲劳损伤的影响。陆文教[6]研究了轮轨磨耗对车辆动力学性能及轮轨接触损伤特性的影响，发现车轮磨耗后(踏面磨耗均匀，轮缘磨耗明显)，表面疲劳指数比标准轮轨时的大，出现滚动接触疲劳的可能性增大。陶功权等[7]对比分析了不同磨耗车轮与标准CN60钢轨匹配时，利用三维弹性体非Hertz 滚动接触理论及其数值程序CONTACT 以及三维轮轨接触有限元模型计算轮轨接触应力的算法，发现CONTACT程序计算得到的轮轨接触斑面积小于有限元计算结果，但CONTACT计算得到的轮轨间最大接触压力和最大等效应力大于有限元结果。针对车轮磨耗后容易出现的多点接触问题，2 种算法误差较大，采用有限元计算结果更可靠。由于有限元方法计算轮轨接触应力时不受弹性无限半空间和材料弹性假设限制，赵腾等[8]建立了不同轮缘磨耗程度的轮轨弹塑性接触模型，发现车轮轮缘厚度由32 mm 磨耗至27 mm 过程中，与磨耗钢轨匹配关系较好，接触斑面积较大，轮缘部分的接触等效应力较小。结合现场试验和有限元方法，FRÖHLING等[9]研究了车轮踏面凹陷磨耗导致的滚动接触疲劳损伤危害问题，讨论了车辆曲线通过性能和凹陷磨耗限值。LIU等[10]基于轮对纵向振动研究车轮踏面剥落机理，发现轮对纵向振动改变了轮轨接触特性、力学特性及接触面上主应力方向，导致轮轨接触面疲劳，最终导致车轮踏面剥落。结合全尺寸制动装置试验和基于有限元法，ESMAEILI等[11]考虑车轮踏面滚动接触疲劳和反复制动同时受到的机械载荷和热载荷问题，对踏面制动进行数值模拟，研究了制动温度和滚动接触疲劳对踏面裂纹的影响。我国某城市地铁线路车辆运营后，车轮普遍出现了凹陷磨耗和踏面接触疲劳剥离现象。经现场调查发现，车轮踏面剥离位置位于轮缘根部附近，呈不规则的网状或鱼鳞状裂纹，沿裂纹处有层状剥离掉块特征。在车辆实际运营过程中，由于车轮凹陷磨耗导致其型面发生显著变化，恶化了轮轨接触相互作用关系。因此，本文作者开展车轮磨耗状态下对轮轨接触状态影响的研究，基于地铁列车运营后出现的车轮踏面疲劳损伤现象，利用有限元软件ABAQUS 建立考虑轮轨真实几何关系的三维轮轨弹塑性接触数值仿真模型，结合轮轨接触几何关系分析，计算车轮不同凹陷磨耗状态下踏面材料应力、应变状态及其对踏面剥离损伤的影响。

1 轮轨接触几何关系分析

轮轨接触几何是研究轮轨关系的基本参数，轮轨型面的匹配程度直接影响列车运行的稳定性、平稳性、曲线通过性能及轮轨接触力和磨耗等。

1.1 凹陷磨耗车轮廓形及磨耗分布

现场试验调查发现全列车轮中80%以上的车轮踏面磨耗量大于2 mm，50%以上的车轮踏面凹陷量(车轮踏面范围内，凸起与凹陷部分的差值)大于0.4 mm，但钢轨磨耗比较轻微。定义T1，T2和T3 为3 种不同踏面磨耗量轮对，其中T1 为标准LM型车轮踏面。

图1所示为3种不同磨耗状态的车轮廓形和磨耗分布情况，车轮磨耗量统计见表1。由图1 和表1可知：车轮轮缘磨耗轻微，踏面磨耗较严重。由图1可见：车轮踏面主要凹陷磨耗区域为车轮踏面横向位置-30 ～ 50 mm，且在-30 ～ -20 mm 处存在较明显的磨耗突变。

1.2 轮轨接触点位置

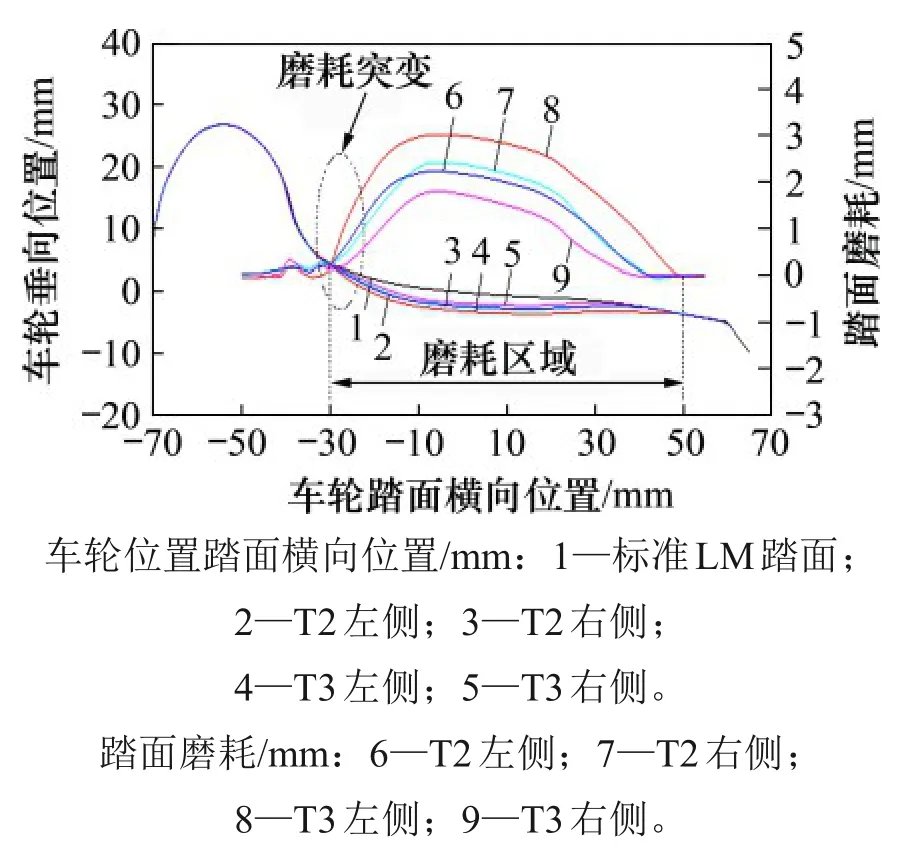
图1 车轮廓形及踏面磨耗分布Fig.1 Wheel profile and tread wear distribution

表1 车轮磨耗量统计Table 1 Wheel wear statistics

车轮出现凹陷磨耗后会严重影响轮轨接触点位置，选取不同踏面磨耗状态(3 种工况)的车轮与60 kg·m-1标准钢轨进行轮轨接触几何关系的数值计算(不考虑摇头角)。其中，车轮名义滚动圆半径为420 mm，轨距为1 435 mm，轨底坡为1/40，轮对横移量为-9～9 mm，每隔0.5 mm 计算1 个接触点。

图2 所示为不同工况下轮轨接触点对分布图。图2中，正值表示轮对向左侧横移，负值表示轮对向右侧移动，0表示轮轨对中接触。图2(a)中，T1轮对发生横移时轮对接触点位置随横移量基本均匀分布，接触状态良好。图2(b)和(c)中，车轮凹陷磨耗后轮轨接触几何呈强非线性特性。T2 左侧车轮横移-8～0 mm 和右侧车轮横移 0.5～8.0 mm 时，轮对接触点位置分别集中在车轮踏面横向位置-30 ～ -20 mm 或 20～30 mm。T3 左侧车轮横移-8.0 ～-0.5 mm和右侧车轮横移0～8.0 mm时，轮对接触点位置位于车轮踏面横向位置-32 ～-20 mm或20～32 mm。另外，轮轨对中接触时，在多个平衡位置处轮轨接触点出现了特别明显的跳跃，导致在跳跃处易产生两点接触，轮对运行会伴随有一定的冲击振动。

若考虑线路不平顺时轮轨接触点位置将会在不考虑不平顺时的轮轨接触点位置附近波动，因此凹陷磨耗车轮的轮轨接触点分布位置都较接近。横移量为0～8.0 mm或-8.0 ～-0.5 mm时，主要接触区域位于车轮车轮踏面横向位置-32 ～-20 mm 或20～32 mm。当车辆频繁通过小半径曲线时，易造成该区域轮轨接触频次较多，由于踏面磨耗突变导致的轮轨接触应力较大，踏面材料易发生疲劳剥离损伤。这与现场调查发现的车轮踏面剥离位置基本吻合。

1.3 滚动圆半径差

列车在运行过程中受外界激扰和轮轨系统本身的影响容易产生蛇行运动，伴随出现轮对不同横移现象[12]。带有凹陷磨耗车轮的车辆在实际线路运行时，滚动圆半径差在不同横移量时会发生明显的变化。图3所示为T1，T2和T3轮对滚动圆半径差与轮对横移量之间的关系。由图3 可知：T1在横移量为-9～9 mm 范围内滚动圆半径差变化较平缓；T2 和 T3 在横移量为 0～2 mm 和-2～0 mm 范围内滚动圆半径差增大，在横移量为2～8 mm 和-8 ～-2 mm 的滚动圆半径差值变化相对缓慢。当凹陷磨耗车轮通过小半径曲线时，轮对横移量增大，车轮滚动圆半径差增大，轮轨纵向蠕滑力随之升高，车轮踏面磨耗和疲劳损伤增大[12]。

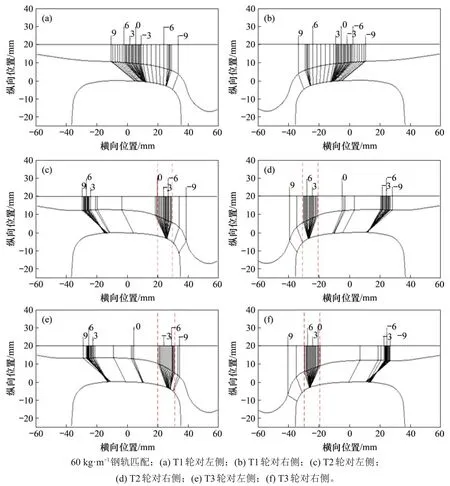
图2 不同工况下的轮轨接触点对图Fig.2 Wheel-rail contact point diagrams under different conditions

以上轮轨接触几何关系表明车辆通过小半径曲线时，轮轨在磨耗突变区容易集中接触，而现场观测到的车轮滚动接触疲劳裂纹就发生在此区域，在车轮磨耗突变区域，轮轨接触半径较小，轮轨接触应力较高，材料容易发生塑性变形，很难用解析法对其分析[13]。虽然KULKARNI 等[14]建立了弹塑性滚动接触问题的分析方法，但方法过于简化，且其前提假设是满足赫兹接触条件，无法反映真实轮轨关系，需考虑非赫兹接触。下面基于轮轨接触几何分析结果，通过建立考虑轮轨真实几何和材料弹塑性本构关系的三维轮轨接触数值模型，进一步探明车轮凹陷磨耗对轮轨接触区域的踏面接触应力及踏面剥离的影响。

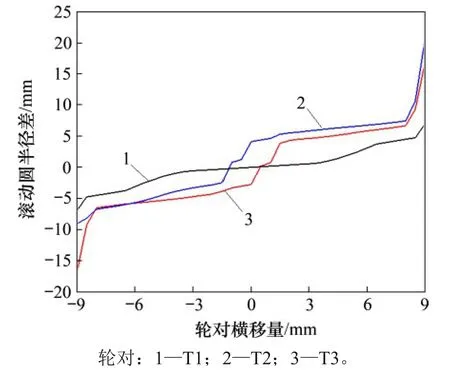
图3 滚动圆半径差与横移量之间的关系Fig.3 Relationship between radius difference of rolling circle and transverse displacement

2 三维弹塑性轮轨接触有限元模型

利用有限元软件ABAQUS 建立三维弹塑性轮轨接触有限元模型，如图4所示。模型考虑了不同凹陷磨耗状态车轮、60 kg·m-1标准钢轨和轨道板实体模型，具体参数见表2。

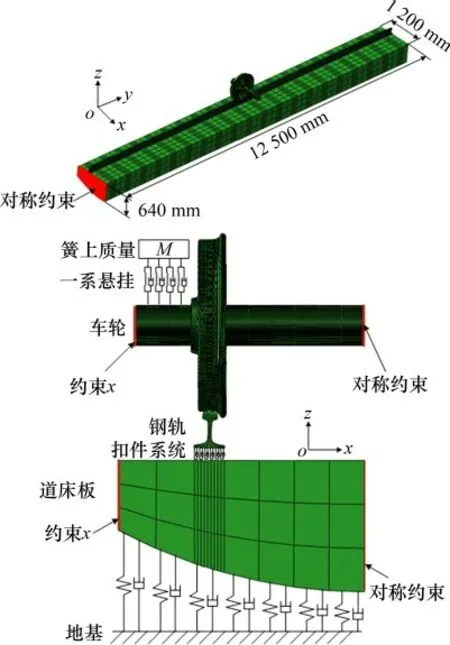
图4 三维弹塑性轮轨接触有限元模型Fig.4 Finite element model of three-dimensional elasticplastic wheel-rail contact

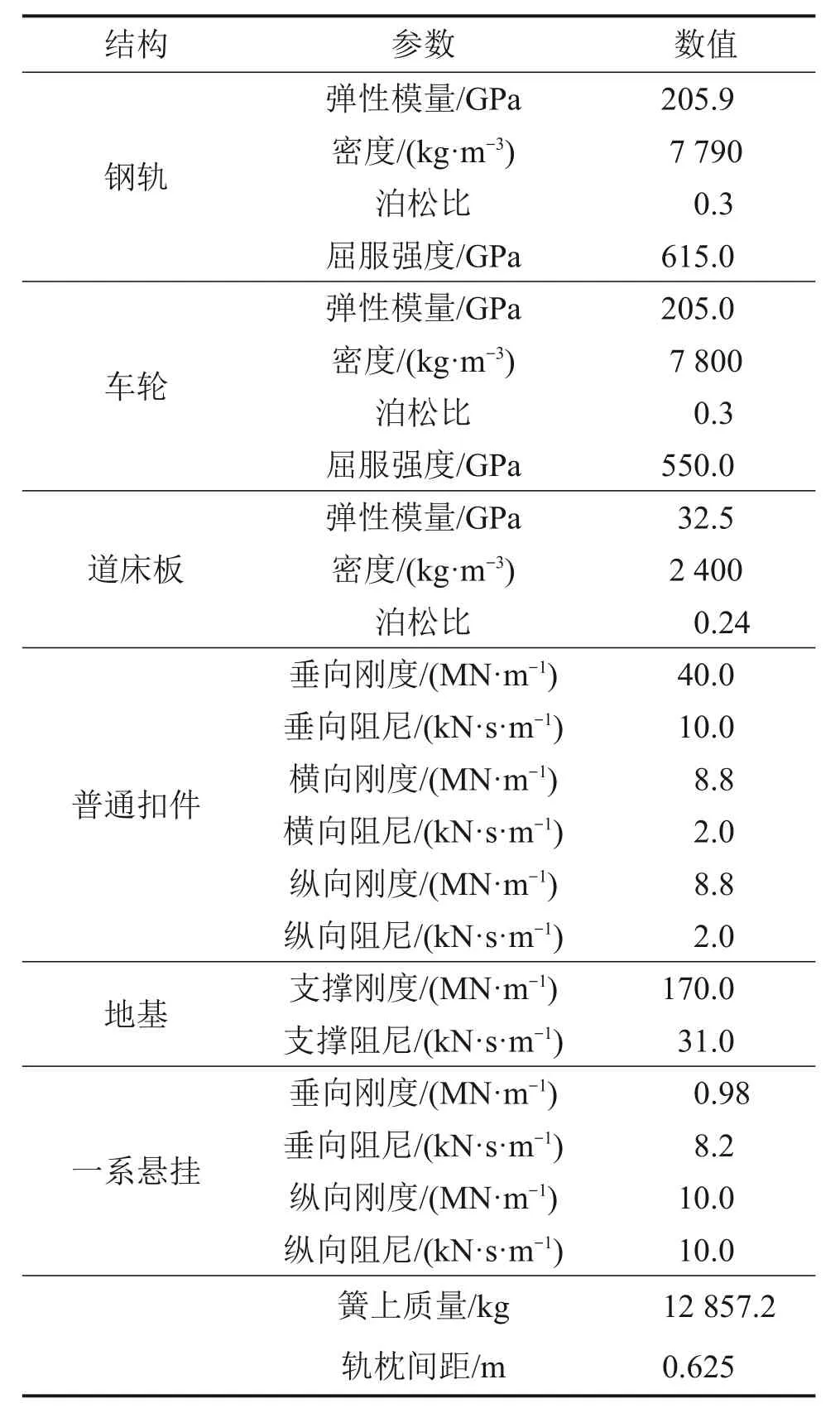
表2 三维弹塑性轮轨接触有限元模型结构参数Table 2 Structure parameters for finite element model of three-dimensional elastic-plastic wheel-rail contact

张宝安等[15]的研究表明当轮对横移量超过5 mm时，轮轨的结构柔性会导致轮轨接触参数发生明显变化，因此在该模型中将轮对考虑为柔性是必要的。模型中未将轨枕和扣件实体考虑在内，两侧离散支撑的扣件系统由间距为50 mm 的20 组弹簧阻尼单元模拟，且考虑了垂横纵方向刚度阻尼特性。将车辆簧上质量M等效为一质量点，并通过一系悬挂(弹簧阻尼单元)与车轴相连。轮轨接触类型采用“面－面”接触，法向接触关系定义为“硬”接触，切向接触关系采用罚函数的摩擦公式定义，轮轨摩擦因数为0.5。为了分辨接触斑内接触压力的分布状态，将轮轨接触区域网格细化，其他区域进行过渡稀疏网格划分，最小单元尺寸为1 mm。车轴对称面横向(x)对称约束，端面横向位移约束；钢轨端面纵向(y)对称约束；轨道板对称面横向对称约束，端面纵向对称约束，侧面横向位移约束。实体模型采用C3D8R 八节点六面体单元离散，共673 076 个节点和585 688 个单元。因考虑到轨道、车轮和轨道板的对称性，本模型只取车轮、钢轨和轨道板的一半建模，以提高求解效率[16]。模型中车轮沿横向平移施加横移量，沿垂向(z)调整接触主从表面的初始位置，且在轮轨接触时设置误差限度使得车轮与钢轨法向接触，确保轮轨接触求解完全收敛。

考虑车轮磨耗突变接触区域的局部塑性变形，轮轨材料采用双线性随动强化弹塑性材料模型，材料本构关系如图5 所示。钢轨材料为U75V，车轮材料为CL60，屈服条件为Von-Mises 屈服准则。线性强化塑性材料模型的应力-应变方程[17]为

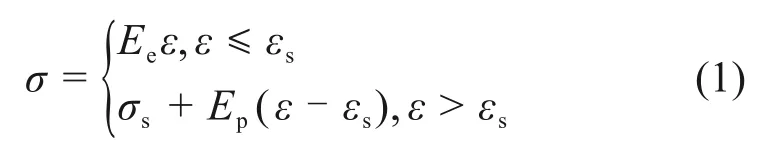
式中：σ为应力；ε为应变；σs为屈服极限；Ee为弹性模量；εs为屈服点处总应变；Ep为应变强化模量；钢轨和车轮Ep为17.254 GPa。

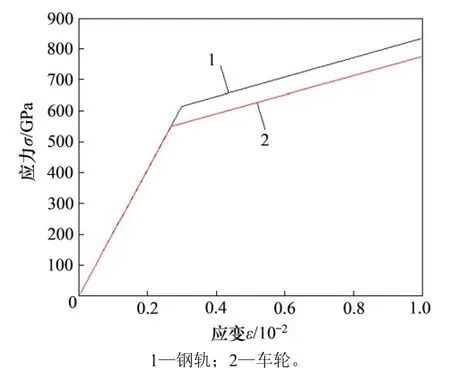
图5 轮轨材料本构关系Fig.5 Constitutive relationship of wheel-rail material

3 结果分析

利用建立的轮轨接触有限元模型，计算分析轮对不同横移量下(-9～9 mm)轮轨接触参数(包括轮轨接触斑面积、最大接触压力、Von-Mises 等效应力、等效塑性应变)及其对应的变化趋势。

车轮发生凹陷磨耗后，轮轨主要接触点位于车轮踏面横向位置20～32 mm或-32 ～-20 mm。图6所示为典型的轮对横移量为-6 mm时轮轨接触斑情况。图中，a和b分别为接触斑长轴和短轴，A为接触斑面积，x为接触斑中心与钢轨中心线的相对距离。由图6 可知：3 种工况轮轨接触斑形状有显著变化(轮轨接触斑面积分别为107.3，57.3 和57.4 mm2)，T1 轮轨接触斑近似圆形，T2 和 T3 轮轨接触斑为沿纵向狭长椭圆形。值得注意的是，凹陷磨耗车轮相对标准车轮的轮轨接触斑中心位置向钢轨内侧偏移约6.7 mm，接触位置在钢轨轨距角或轮缘根部附近。凹陷磨耗车轮狭长的轮轨接触斑面积使得相同载荷下轮轨接触应力较高，导致在该接触位置中心处容易出现滚动接触疲劳。对于T1 车轮(标准车轮踏面)，轮轨最大接触应力为960 MPa；对于凹陷磨耗T2 和T3 车轮，轮轨最大接触应力分别为1 465 和1 490 MPa，与T1 车轮相比，增加了约53%。

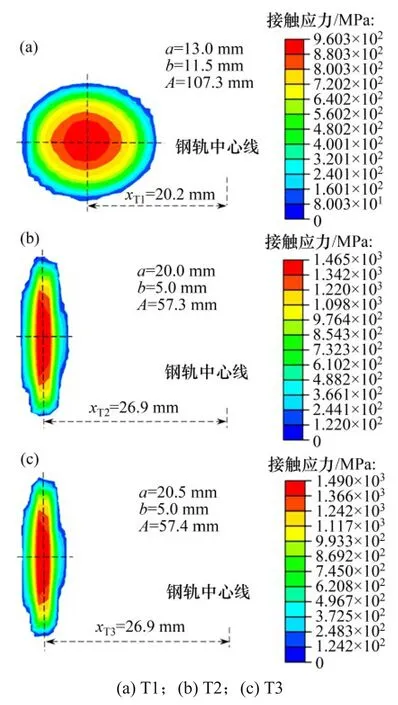
图6 轮轨接触斑面积Fig.6 Area of wheel-rail contact patches

图7 所示为轮对不同横移量时轮轨接触Von-Mises 等效应力变化趋势。由图7 可知：当轮对横移量为正时，T2 和T3 的Von-Mises 等效应力变化趋势基本相同；当轮对对中接触时，T1 的Von-Mises 等 效 应 力 最 大 (605 MPa)，T3 的 最 小(460 MPa)，这是因为凹陷磨耗车轮在横移量为0 mm时，轮轨呈曲面接触，凹陷磨耗量较大的车轮接触斑面积较大；当轮对横移量为负时，3种工况下轮轨接触Von-Mises等效应力差异明显，在凹陷磨耗车轮的轮轨频繁接触区域内(轮对横移量为-0.5～-8.0 mm)，T2 和 T3 轮轨 Von-Mises 等效应力剧增。

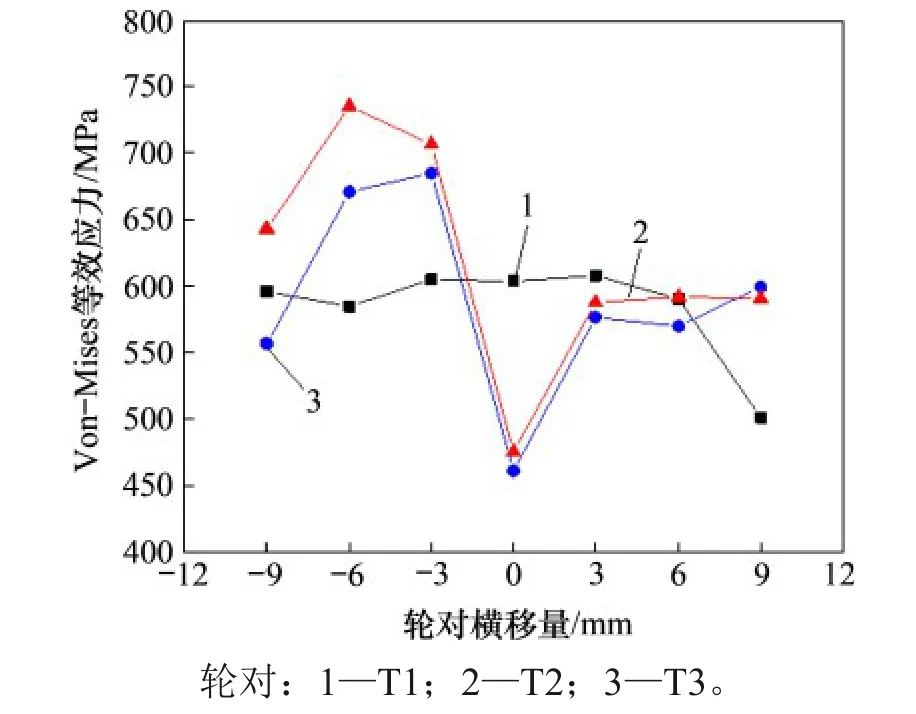
图7 Von-Mises等效应力随轮对横移量变化趋势Fig.7 Trend of maximum Von-Mises equivalent stress of wheel-rail with wheelset transverse shift

图8所示为车轮横移量为-6 mm时轮轨接触区域Von-Mises 等效应力云图。由图8 可知：3 种工况下轮轨接触区域均出现了较明显的等效应力集中区域，凹陷磨耗车轮相比标准车轮的等效应力集中点向钢轨内侧偏移倾向，其位置靠近轮缘和钢轨轨距角。为了表征Von-Mises等效应力影响范围，分析Von-Mises等效应力沿车轮踏面接触斑深度方向的变化趋势，如图9所示。由图9可知：凹陷磨耗车轮在接触斑表面以下0～3.6 mm 深度范围内Von-Mises 等效应力最大，而标准车轮Von-Mises 等效应力较小。另外，与T1 轮对相比，T2和T3车轮对Von-Mises应力出现的位置更接近车轮表面；随着深度的增大，3 种工况下Von-Mises 等效应力逐渐减小。

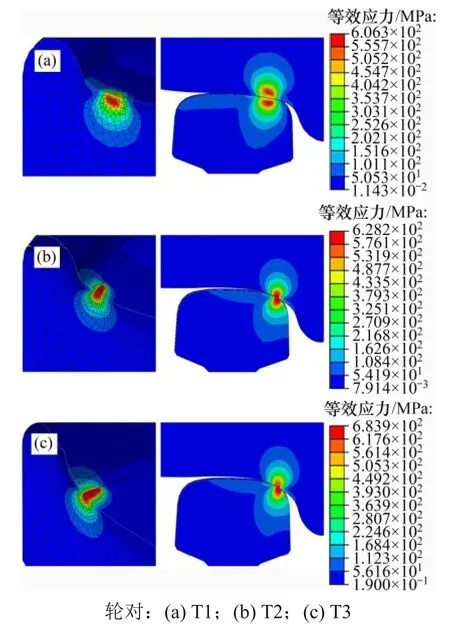
图8 轮轨Von-Mises等效应力云图Fig.8 Von-Mises equivalent stress distribution of wheel-rail

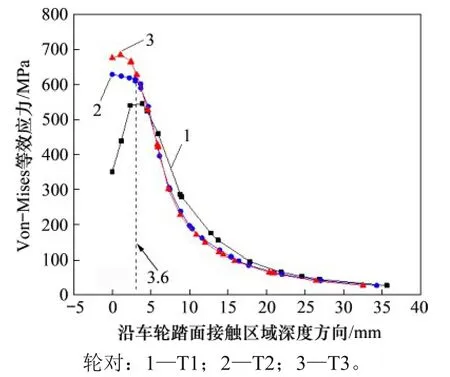
图9 Von-Mises等效应力沿接触斑深度方向的变化Fig.9 Variation of Von-Mises equivalent stress along depth of contact patch

图10 所示为轮对不同横移量时轮轨等效塑性应变变化情况。由图10 可知：当轮对横移量为负时，凹陷磨耗车轮相比标准车轮的轮轨等效塑性应变急剧增大，且在横移量为-9～-6 mm时其值达到最大。这主要是因为横移量为负时轮轨接触点位置发生较大偏移，轮轨接触斑面积变小和应力集中导致的。图11 所示为等效塑性应变最大值处的轮轨等效塑性应变云图。由图11可知：T1轮轨等效塑性应变较小，塑性变形区主要集中在车轮次表层。T2和T3轮轨等效塑性应变较大，T3等效塑性应变约为T2 的4.35 倍，为T1 的151 倍，变形区集中在车轮表面且沿车轮轮缘圆周狭长分布。凹陷磨耗车轮较大的塑性应变容易引起接触表面材料的塑性流动和残余应力的产生。车轮踏面出现凹陷磨耗后，车辆频繁地通过小半径曲线，在长期反复滚动接触载荷作用下，易在磨耗突变区造成较高的等效应力和等效塑性应变，产生局部永久性累积损伤，导致轮缘根部表面材料剥离损伤，这与现场观察到的踏面剥离基本吻合。

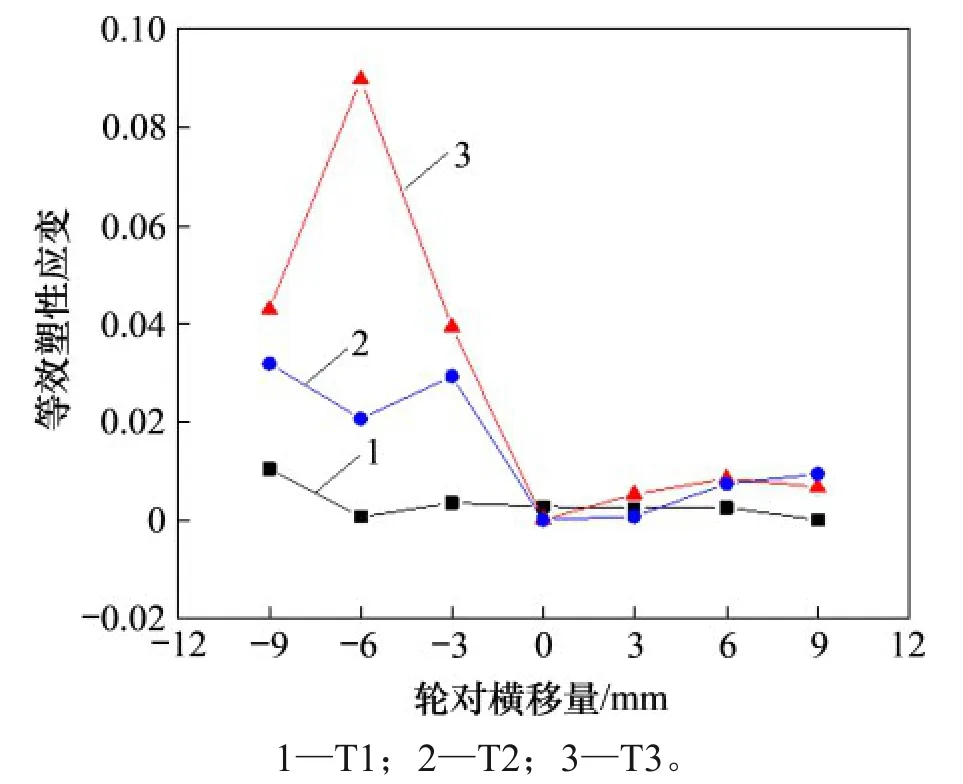
图10 轮轨等效塑性应变随轮对横移量的变化Fig.10 Change of equivalent plastic strain of wheel-rail with wheelset transverse shift

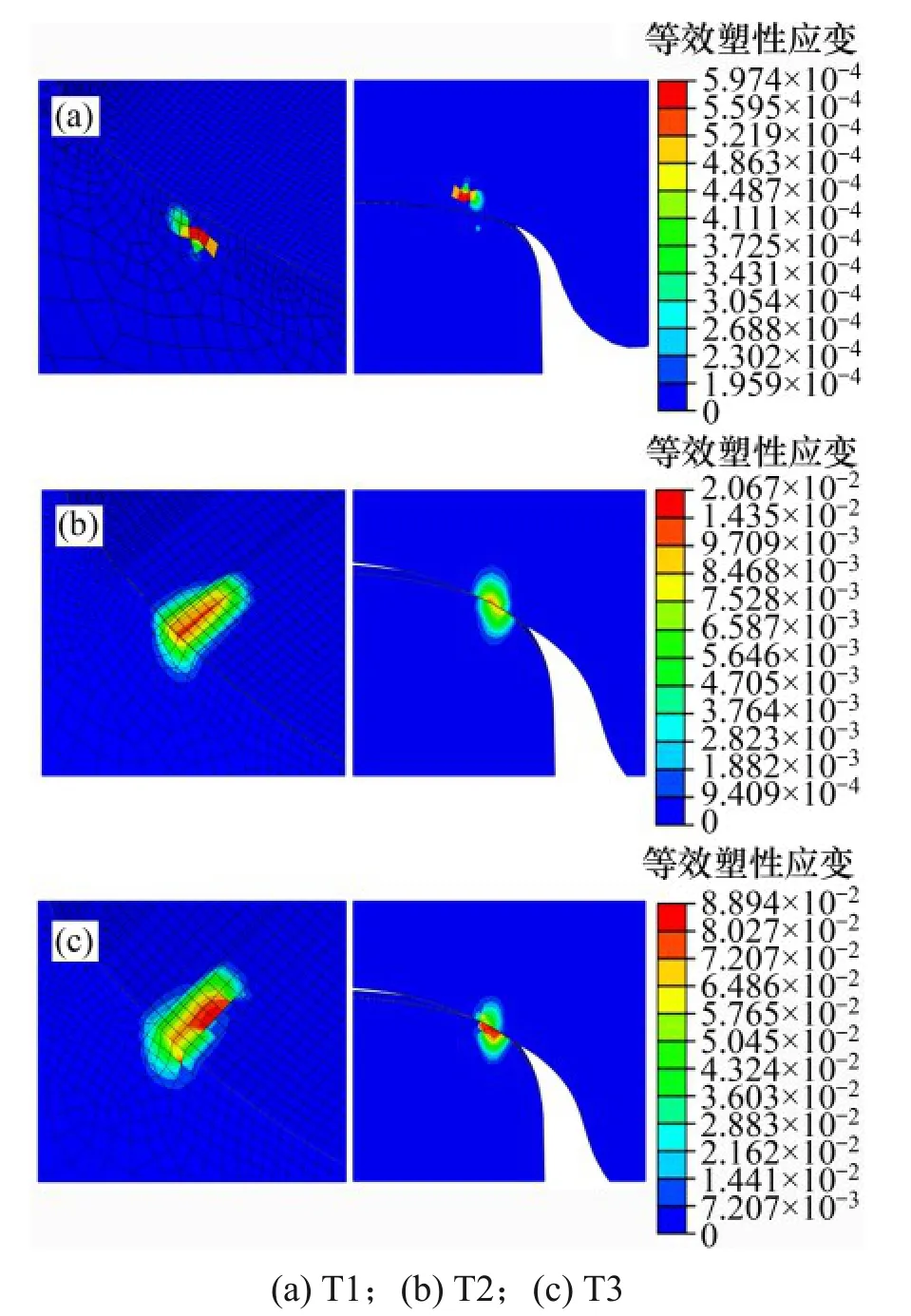
图11 轮轨等效塑性应变云图Fig.11 Equivalent plastic strain distribution of wheel-rail

4 结论

1)地铁列车车轮踏面主要凹陷磨耗区域为车轮踏面横向位置-30～50 mm，全列车轮中80%以上的车轮踏面磨耗量大于2 mm，钢轨磨耗轻微。轮轨接触几何关系呈强非线性特性，其接触点位置主要集中在车轮踏面横向位置20～32 mm 或-32 ～-20 mm，与现场调查发现的车轮踏面剥离位置吻合。且当轮轨对中接触时，在多个平衡位置处轮轨接触点位置出现了明显的跳跃。

2)车轮不同凹陷磨耗状态下的轮轨接触状态差异显著。尤其在磨耗突变区(-30 ～-20 mm)轮轨集中接触，接触斑面积呈狭长椭圆分布，导致相同载荷下轮轨接触应力较大。

3)当轮对向外轨横移时，车轮凹陷磨耗接触区域材料易进入屈服状态，此时车轮踏面沿接触斑深度方向0～3.6 mm范围内Von-Mises等效应力最大，踏面表层材料等效塑性应变最大。当车轮踏面出现凹陷磨耗后，车辆频繁地通过小半径曲线时易在磨耗突变区造成较高的等效应力和等效塑性应变，从而导致轮缘根部表面材料产生剥离损伤。