立体几何问题的正确打开方式:“算”与“思”(上)
2020-07-16曾荣
曾 荣
同学们,你们知道立体几何研究什么吗?在高考中是怎么考查的吗?
近几年的全国卷立体几何解答题,绝大部分采用“一半证明,一半计算”的方式,即第一问主要考查线面位置关系的证明,第二问涉及角与距离或体积的计算.在解决几何计算问题时,综合几何法和向量坐标法是两种常用的方法.
敲黑板
立体几何主要研究现实世界中物体的形状、大小与位置关系.高考立体几何试题考查的重点内容为点、线、面位置关系的判断、证明和计算等问题.
依托空间向量,注重计算,算思结合
例1 (2019年高考全国I理科卷)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
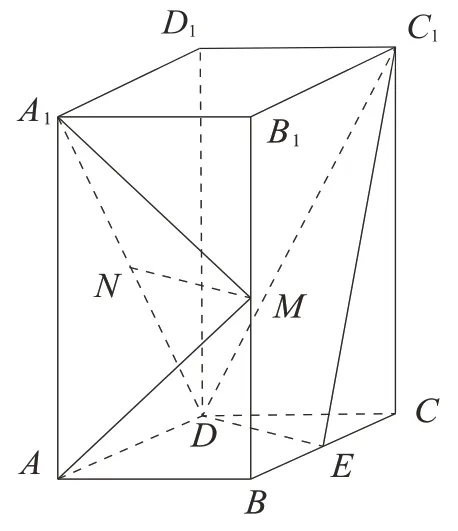
图1
【思路剖析】
第一问思路:证MN∥平面C1DE的大方向是证MN∥ED.通常的方法有:
①直接法:将MN,DE置于四边形MNDE中,证明四边形MNDE是平行四边形;
②间接法:通过第三条直线过渡证明平行关系.取AD的中点F,连结FB.通过FB∥MN,FB∥ED证明MN∥ED.
第二问思路:本题研究的几何体是直棱柱,故z轴的方向是明确的.试题中已知底面是菱形,且∠BAD=60°,故能否结合这一图形特征挖掘垂直关系,建立合适的坐标系成了解决问题的关键.
①建系方案
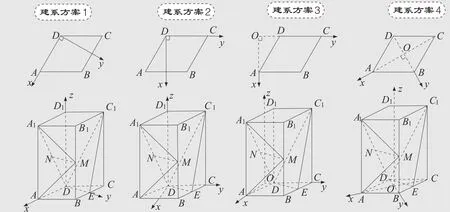
图2
②方案比较

方案方案1方案2方案3方案4以上四种方案,各有优点,结合本题的图形特征和数据特征,本题采用方案1、2、4比较合适相关点的坐标A(2,0,0),B(1,3,0),C(-1,3,0),D(0,0,0)E(0,3,0),M(1,3,2),N(1,0,2),A1(2,0,4)A( 3,-1,0),B( 3,1,0),C(0,2,0),D(0,0,0)E(3 2,3 2,0),M( 3,1,2),N(3 2,-1 2,2),A1( 3,-1,4)A( 3,0,0),B( 3,2,0),C(0,3,0),D(0,1,0)E(3 2,5 2,0),M( 3,2,2),N(3 2,1 2,2),A1( 3,0,4)A( 3,0,0),B(0,1,0),C(-3,0,0),D(0,-1,0)E(-3 2,1 2,0),M(0,1,2),N(3 2,-1 2,2),A1( 3,0,4)优点直接利用了图形中已有的垂直关系AD⊥DE,建系方式便捷与方案1 位置不同,本质一样,其中AMA1的法向量已知,无需另求需要作出辅助线,建系方式相对隐蔽,各点的坐标均为正数具有对称性,点的坐标容易写出
【规范解答】
(1)证法一:连结B1C,ME.
在直四 棱柱ABCD-A1B1C1D1中,A1B1∥AB,AB∥DC,
A1B1=AB,AB=DC,
所以A1B1∥DC,A1B1=DC.
所以四边形A1DC B1为平行四边形.
所以B1C∥A1D且B1C=A1D.
因为M,E分别为BB1,BC的中点,
所以ME∥B1C,且.
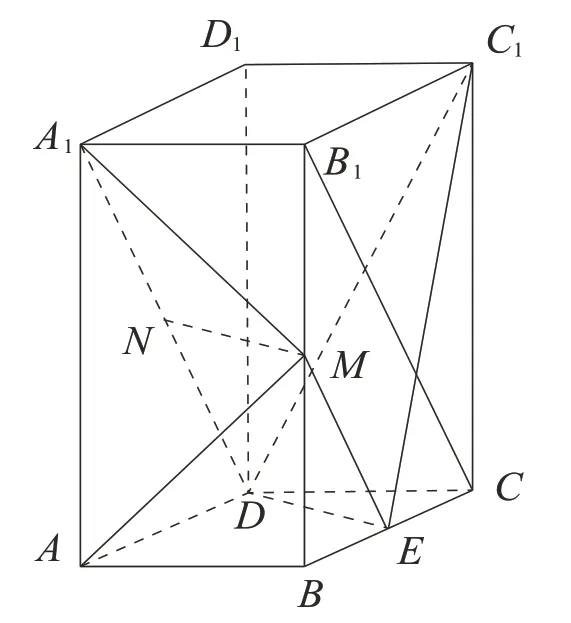
图3
又因为N为A1D的中点,所以.
所以ME∥ND,ME=ND,
因此四边形MNDE为平行四边形,MN∥ED.
又MN⊄平面C1DE,DE⊂平面C1DE,所以MN∥平面C1DE.
证法二:请同学们参考证法一的过程自行完成.
(2)解法一:在直四棱柱ABCD-A1B1C1D1中,D1D⊥DA,D1D⊥DE.
因为底面是菱形,∠BAD=60°,所以三角形BCD为等边三角形,
因为E是BC的中点,所以DE⊥BC,所以DE⊥DA.
以D为坐标原点,DA,DE,D1D所在的直线为x轴、y轴、z轴,建立如图4所示的空间直角坐标系D-xyz.
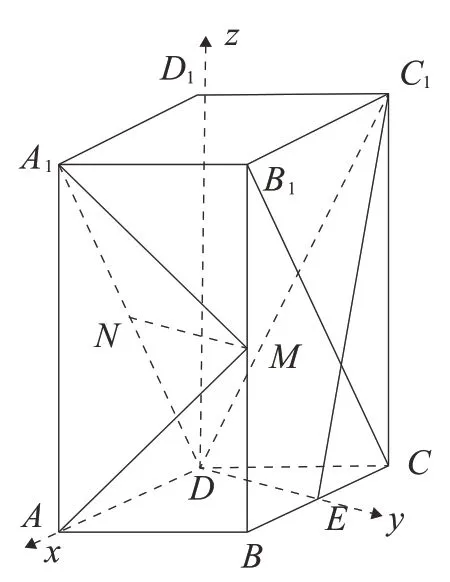
图4
设m=(x,y,z)为平面A1MA的法向量,则
设n=(p,q,r)为平面A1MN的法向量,则
所以二面角A-MA1-N的正弦值为.
其他解法:请同学们参考解法一的过程自行完成.
【归纳提升】

