消纳大规模风电的电-气互联系统鲁棒区间调度模型与方法

2020-07-15王文睿瞿凯平王克英史守圆

控制理论与应用 2020年6期

王文睿，瞿凯平，余涛，王克英，史守圆

(华南理工大学电力学院，广东广州 510640)

1 引言

作为能源互联网的重要基础和过渡[1-2]，电-气互联系统(integrated electric and gas system，IEGS)将电力网络和天然气网络通过燃气机组和电转气(power to gas，P2G)装置紧密耦合在一起，实现了可再生能源的高效利用.而在能源互联网的实现条件下，风能将成为其主要的电力发电来源[3]，如何消纳带有发电不确定性的风能因此成为IEGS面临的一个主要挑战.

文献[4-6]采用随机规划处理IEGS中的风电不确定性问题，随机规划依据概率分布抽取大量场景，以各个场景下成本的概率加权值作为决策目标，但由于难以获得准确的概率分布，导致其决策的可靠性降低[7].文献[8]提出了基于自适应鲁棒优化方法(adaptive robust optimization，ARO)的IEGS机组组合模型，ARO将调度分为预决策和再决策两个阶段，再决策阶段在风电不确定性被观测后，通过调整燃气机组和P2G装置的出力，使系统过渡到安全状态.但文献[8]在应对风电出力波动进而调整燃气机组的出力时忽略了到对气网运行约束的影响，为此文献[9]基于ARO提出了进一步考虑气网运行约束的经济调度和备用配置模型，其将燃气机组的风电备用范围转换为进气范围，并将进气范围构造为不确定性集合形成气网可行性检验子问题，最终构成一个电网调度与备用配置-风电不确定校验-气网可行性检验的3层优化问题，由此可见，基于ARO形成的进一步气网运行约束的IEGS鲁棒调度模型结构复杂，且由于管道气流约束为非凸，导致其求解进一步难度增大.

P2G技术具有响应速度快、调度特性灵活的特点[10]，当风电波动时，P2G装置可配合燃气机组进行功率调节以追踪风电出力.文献[8，11-12]在再决策阶段中将P2G装置作为自由调节的手段，忽略了P2G运行成本较高[10]特点，在日前未对P2G的风电备用容量进行整定，其经济性在一定程度上脱离于现实情况;文献[9]并未将P2G装置纳入其数学模型中，忽视了P2G装置进一步消纳风电的作用，仅在日前考虑整定燃气机组应对风电波动的备用容量.

针对以上研究背景，为了更简单有效地解决IEGS引入风电不确定性后难以考虑对气网运行的影响这个问题，同时充分计及P2G装置应对风电波动时的配置问题，本文基于仿射可调节鲁棒优化方法(affinely adjustable robust optimization，AARO)[13-14]提出了一种IEGS鲁棒区间调度模型.相较于ARO，AARO简化了再调度阶段，将再调度决策阶段的调整措施描述为自动发电控制(automatic generation control，AGC)机组的仿射校正过程[15]，基于此可将IEGS风电鲁棒调度模型描述为一个单层优化问题.具体而言，本文的贡献主要如下:

1) 计及燃气机组参与AGC调节响应和P2G装置追踪风电波动，建立了一种IEGS鲁棒区间调度模型，通过模型优化得到风电可消纳区间、AGC机组和P2G装置的允许出力区间，进而将允许出力区间转换为最大耗气量和最小耗气量场景以进一步校验气网的可行性.

2) 为提升模型的鲁棒性，将AGC机组和P2G装置的风电承担系数作为待优化变量，并对因此引入的非线性项进行松弛处理.

3) 设计了一种计及再调整的日后校正过程，通过对不同的算例场景进行蒙特卡洛模拟，对比分析仿真结果后验证了本文所提模型与方法的有效性.

2 IEGS鲁棒区间调度模型

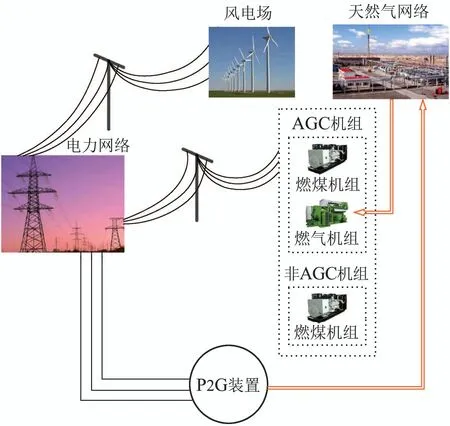
图1 系统框架Fig.1 Framework of system

在满足电网和气网约束条件下，本文所提模型旨在通过以下资源来实现调度的安全性与鲁棒性:

1) AGC机组:燃气机组和部分燃煤机组参与AGC调节，当风电场实际出力在风电容许区间内波动时，即时，可通过AGC机组进行调节使系统稳定过渡到安全状态.

2) 非AGC机组:部分燃煤机组不参与AGC调节，其出力严格追踪日前计划值.

3) P2G装置:考虑在电网装设P2G装置参与风电消纳，P2G作为电网负荷在基点状态下消纳一部分风电:当风电实际出力时，P2G装置继续消纳这部分弃风功率，以进一步提高风电消纳区间的上限，将提高后的上限称为“P2G风电上限”，计为

4) 风电场:风电场在基点状态下追踪预测区间的期望出力，即利用风电基态出力在追踪期望出力在实际调度中，风电场严格追踪区间内的任意风电出力.

根据以上叙述，将各类风电出力的关系描述为

在IEGS鲁棒区间调度中，风电实际出力在风电容许区间波动时所产生的风电功率不平衡量由AGC机组承担，而非AGC机组则严格执行基态出力值;而当风电实际出力大于风电容许区间上限时，由P2G装置继续承担风电不平衡量.引入机组风电承担系数和P2G装置风电承担系数，本文将其设为待优化变量，进而将机组实际出力和P2G实际电功率描述为

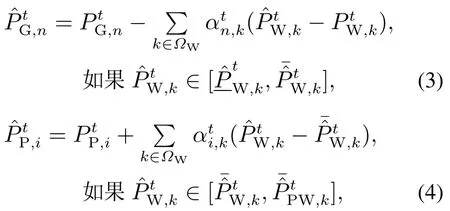
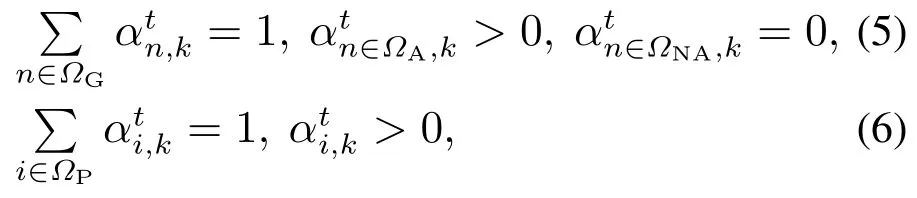
式中:ΩG为所有机组集合;ΩA和ΩNA分别为AGC机组和非AGC机组集合，非AGC机组不承担风电波动;ΩP为所有P2G装置集合.

本文假设风电场出力预测区间服从某种概率分布，期望出力(即预测出力)作为概率分布中最可能出现的情况，系统需要在利用风电基态出力追踪风电预测出力的前提下，使风电容许区间和P2G风电上限也尽可能地追踪风电预测区间，以体现最大化利用风电.为实现上述过程，在优化目标中需添加风电惩罚项:

式中设置φWF，k=200，φW，k=φWP，k=100.

模型以最小化基态供能成本和最大化风电利用为目标:

式中:ΩT，ΩGC，ΩS，ΩC分别为所有时间断面集合、所有燃煤机组集合、所有气源集合和所有储气库的集合;分别为燃煤机组n的煤耗量、P2G装置i 的产气量、气源j 的出气量和储气库的出气量及进气量;cW1=15$/MWh，cW2=30$/MWh，cW1和cW2分别反映了在日前配置AGC机组和P2G装置追踪风电波动的备用容量单位成本.其中，燃煤机组、燃气机组和P2G的耗量特性可描述为

式中 HHV 为天然气的热值系数，HHV=39 MJ/Mm3.

2.1 电网约束

本文采用直流潮流描述电力网络，包括总功率平衡约束、机组出力约束、机组爬坡约束、旋转备用约束、P2G功率约束，以及支路传输功率限制.根据文献[13]可知，在鲁棒区间调度中，无论风电实际出力在消纳区间中如何变化，电网中的所有决策变量均不能超过电网约束的限制，因此可将上述约束的鲁棒区间形式总结如下:

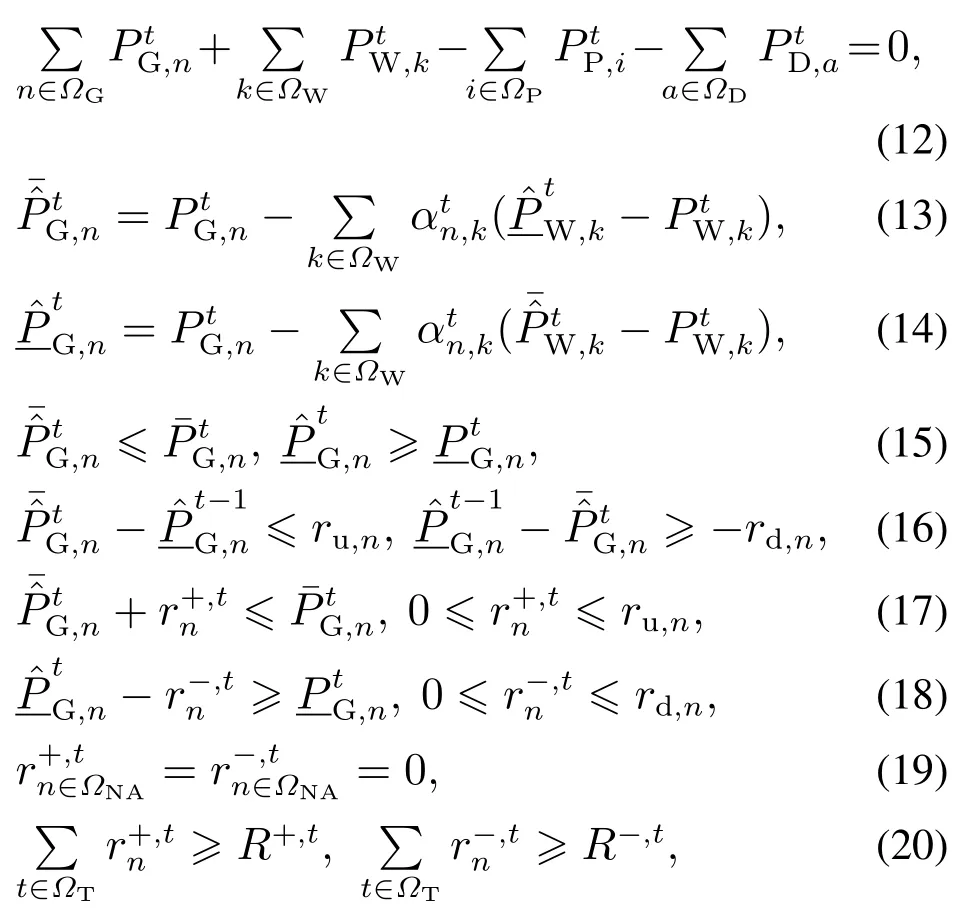
其中:式(12)为总功率平衡约束，式(13)-(15)为机组出力约束，式(16)为机组爬坡约束，式(17)-(20)为旋转备用约束.

为最大程度地减少弃风，目标函数中设置的风电惩罚项系数在数值上比P2G的产气成本大，为防止系统在基态下因为追踪P2G风电上限而消纳更多的P2G电负荷，进而造成基态成本过高，本文限制基态下P2G装置仅在弃风时段启动，可将基态下的P2G功率约束归纳如下:

P2G实际消耗的最大、最小电功率同样不能超出其功率限制:

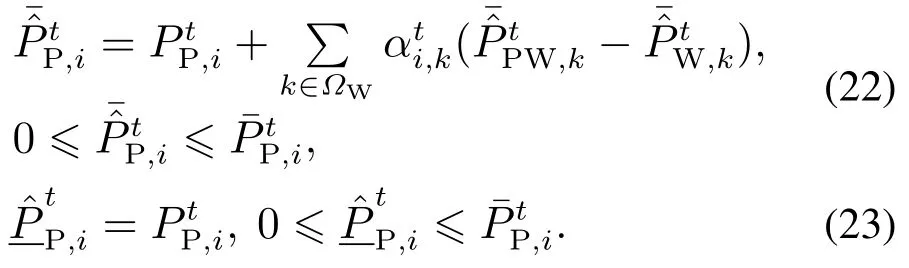
依据上文分析，将风电消纳区间内的潮流约束分为两种情况，即在风电容许区间内和在区间内的线路传输功率均不可以超过限制:

2.2 气网约束

对于一条理想的天然气管道，由于气流传输的缓慢性，其出口气流并不等于入口气流，根据文献[17]，可采用有限差分技术对气流动态特性进行描述:

式中:下标m，n代表天然气网络节点，并分别对应连接管道m-n的首末节点;考虑将管道分为NP段，d为管道分段索引，d=0，1，2，…，NP;分别对应管道m-n第d段的气压和气流.分段后的天然气管道模型如图2所示.

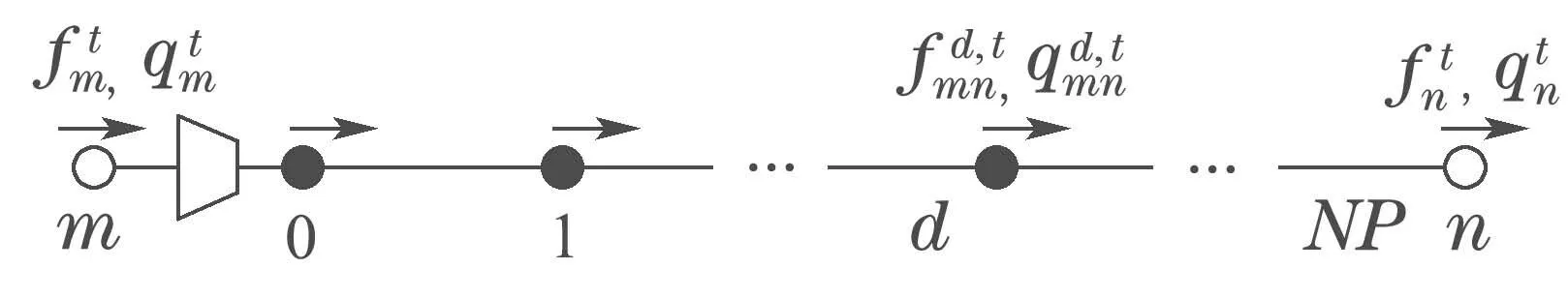
图2 管道模型Fig.2 Model of gas pipe

天然气网络中的管道可分为有加压站管道和无加压站管道.对于无加压站管道，首末端节点的气压有如下关系:

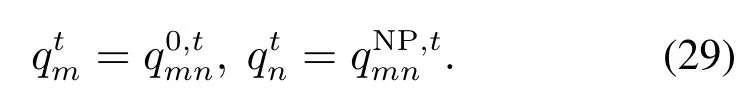
由于加压站消耗的气流量相对于流经的气流很小，本文忽略其耗能而只保留气压升降关系[18]，则对于有加压站管道，其首端节点有如下关系:

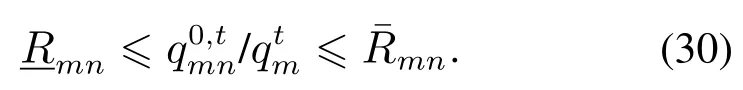
天然气网络中考虑引入储气库作为应对管道故障或需求增长的应急气源，其约束可表示为

气源出力和节点气压需满足上、下限约束:

由式(27)可知，管道首端注入天然气流与末端流出天然气流不相等，首末端相差的天然气流短暂地储存在管道中，称之为“管存”.为了合理使用管存，天然气网络运行一个周期后的管存量将不得低于管存量初始值，为下个调度周期预留一定的调节裕度.为此，需要考虑如下对管存裕度的校验:

根据以上叙述，天然气网络节点m的流量平衡方程可描述为

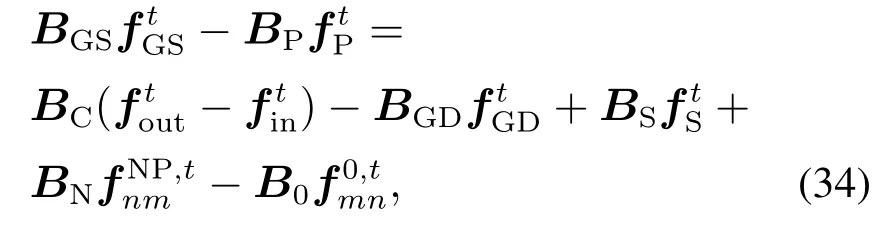
将式(27)-(34)所描述的基态下的气网约束简化为如下紧凑形式:

式中 xg为式(27)-(34)中的气网基态决策变量向量.

为追踪风电波动，燃气机组出力和P2G装置的耗电功率是可调节的，因而除了基态下的气网约束，还需要进一步考虑调节状态下的气网约束，将调节状态下的气网实际决策变量向量表示为式(27)-(34)所描述的调节状态下的气网约束同样可简化为如下紧凑形式:

燃气机组出力和P2G装置的耗电功率的变化将引起气网节点气压和管道流量的改变，本文考虑系统通过调节气源出力和管存来应对波动，储气库则不作为调节资源，调节状态下气源和管存的变化总量应等于燃气组耗气量和P2G进气量的变化总量，因而存在调节状态和基态的耦合约束:

进一步地，将式(36)-(38)所描述的调节状态下的气网约束表示为

由上文分析可知，在调节状态下的燃气机组实际耗气量和P2G装置实际产气量存在如下关系:

3 模型求解

3.1 非线性项的消除

在本文所描述的模型中，由于机组和P2G装置的风电承担系数为变量，在式(13)-(14)(22)(25)-(26)中存在机组和P2G装置的风电承担系数与风电不平衡量相乘的非线性项，使得模型难以得到准确求解.为消除式(13)-(14)和式(22)中的非线性项，可结合式(5)-(6)可做如下转换处理:

式中用机组和P2G装置承担风电波动变量替换原有机组和P2G风电承担系数与风电不平衡量相乘的非线性项，如此替换后的模型并不完全等价于替换前的模型，此时机组对风电的正、负波动采用了不同的承担系数，但这样处理后可以扩大变量的可行域，提高模型的鲁棒性，使目标优化效果更好.

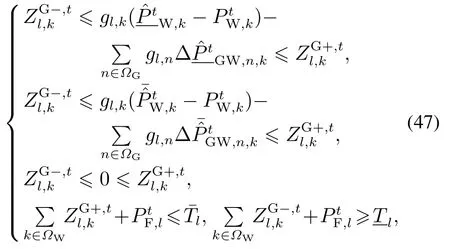
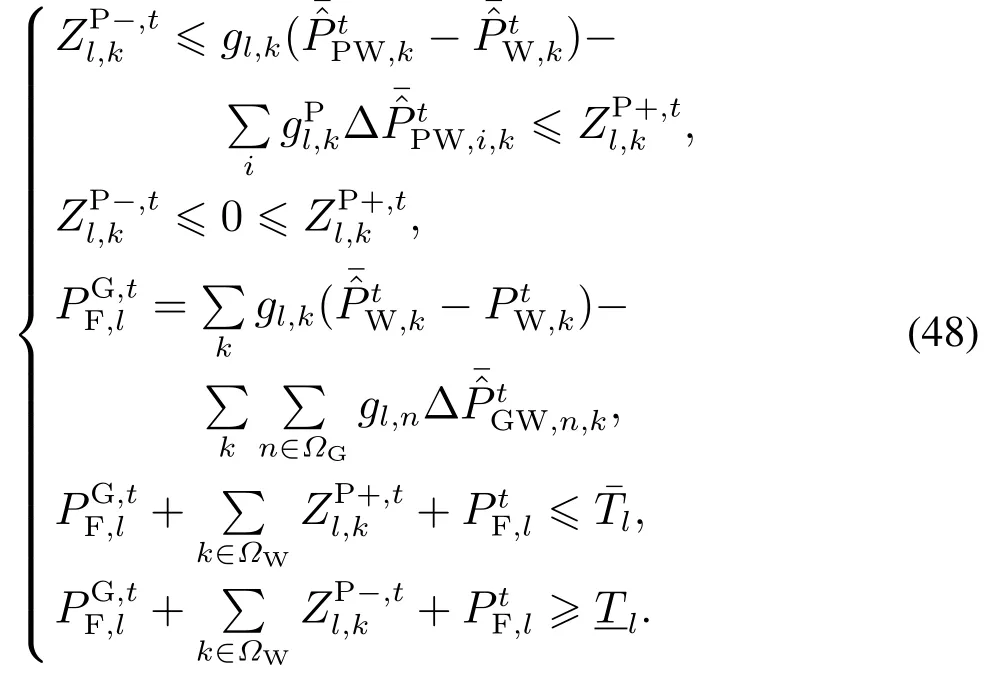
3.2 气流方程的凸化

消除非线性项后，模型的非凸性由式(35)和式(43)-(44)中形如式(28)的管道气流方程造成，此管道气流方程的等式关系可用两个不等式关系表示:

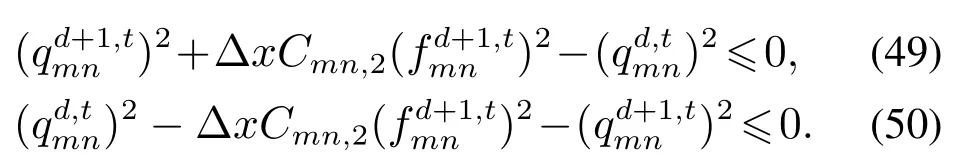
式(49)为一个标准二阶锥约束，其本身为凸约束，则只需对式(50)进行凸化.式(50)是一个典型的凸函数差约束，可根据文献[19]提出的罚凸凹过程进行凸化.用一阶泰勒公式对式(50)中的被减凸项进行近似，同时引入松弛变量对近似后的不等式进行松弛，得到

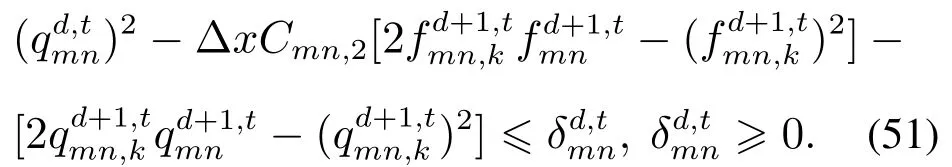
式(51)中，带下标k的变量为常数，其值为上一次迭代过程得到的变量值.罚凸凹过程通过在目标函数中设置惩罚系数ρ不断对进行惩罚，以使松弛域不断紧缩，直至收敛.在迭代初期，对的惩罚很小以便获得一个足够好的初始点，随着迭代进行，对的惩罚逐渐增大，以使趋近于0.此外，罚凸凹过程的收敛准则保证了最后两次的计算结果足够接近.因此，当罚凸凹过程收敛时，式(51)的松弛是紧的.关于罚凸凹过程的收敛性证明可参考文献[19].忽略形如式(51)的凸松弛约束和目标函数中对松弛项的惩罚，进而求出初始点.罚凸凹过程的收敛准则为

式中 δk+1为所有气流方程松弛项所构成的向量.

若式(52)的收敛准则被满足，则停止计算;否则，更新惩罚系数后重复罚凸凹过程，直至满足收敛准则.惩罚系数的更新原则如下:

式中 v为惩罚系数的更新因子，其数值应大于1.

至此，本文所描述模型的求解过程已完全转化为二次规划问题，可采用求解器CPLEX进行迭代求解.

4 算例分析

本文以修改的IEEE39节点电力网络和比利时20节点天然气网络搭建IEGS，电力网络中共有8台发电机组和2个风电场，其中:1，5号机组为燃气机组，其余机组为燃煤机组.考虑1，5，6号机组作为AGC机组，其余机组均为非AGC机组，即系统内所有燃气机组和6号燃煤机组作为AGC机组，并假设风电出力预测区间中点作为风电预测出力值;系统的天然气网络中共有2个气源和4个储气库，2 台燃气机组分别连接于气网的4，10节点，2台P2G装置接入气网的13，14节点.IEGS仿真系统的拓扑图，机组参数、电网负荷和风电出力预测数据，气源、储气库、P2G 参数及罚凸凹过程参数详见附录A.

各个算例场景在求解得到日前调度策略后，需要通过日后校正模型，并采用文献[20]中基于Nataf变换的蒙特卡洛模拟过程进行仿真，进而得到各算例场景的校正成本，具体的日后校正过程及模型详见附录B.假设风电实际可用出力服从正态分布，并以99.9%的概率覆盖风电预测区间，进而抽取100个随机的风电实际可用出力场景进行模特卡洛模拟.为充分说明本文模型的有效性，考虑设置如下4个算例场景:

1) 场景1:传统IEGS确定性调度，其忽略风电出力波动，约束条件均为确定性约束.

2) 场景2:基于AARO的IEGS鲁棒调度，在文献[9]的模型基础上加入P2G装置，考虑在日前优化追踪风电正、负波动的AGC机组备用容量和追踪风电正波动的P2G备用容量由于本文模型风电惩罚项的惩罚系数设置得很大，此时可认为场景3所优化的风电容许区间为仿真系统所能消纳的最大风电波动区间，故将作为限制场景2模型中风电不确定性集合的边界条件，并将不确定性预算参数设定为具体的数学模型详见文献[9].

3) 场景3:IEGS鲁棒区间调度，即本文所提出的完整模型.

4) 场景4:IEGS鲁棒区间调度，在场景3的基础上忽略调节状态下的气网约束.

通过对比场景1-3的调度结果分析本文模型的有效性;通过对比场景3-4的调度结果分析在IEGS鲁棒区间日前调度中考虑调节状态气网约束的必要性.

4.1 仿真结果分析

在求解5个算例场景的日前调度模型后，得到日前调度的基态供能成本，进而将日前调度策略代入校正模型中进行蒙特卡洛模拟，得到各个算例场景的日后校正成本.其中，日后校正成本则包括了弃风、弃负荷成本、AGC燃煤机组(电网)、气源(气网)及P2G出力的调整成本.日后校正成本均为蒙特卡洛场景的平均值，系统的实际调度成本=基态供能成本+校正成本，仿真结果如表1所示.

表1 各调度场景的仿真结果对比Table 1 Result comparison of each scheduling scenario

4.1.1 鲁棒区间调度的有效性分析

在场景1的确定性调度中，其风电和机组出力情况如图3和图4所示.由图3和图4可知，场景1的风电基态出力曲线完全贴合于预测出力曲线，系统能够完全追踪预测出力，而P2G装置仅在弃风时段4-5启动，以消纳基态下的弃风;由于燃气机组和AGC燃煤机组的发电成本较高，因而机组出力大部分由非AGC机组承担，燃气机组和AGC燃煤机组的出力在整个调度周期中维持较低的水平.

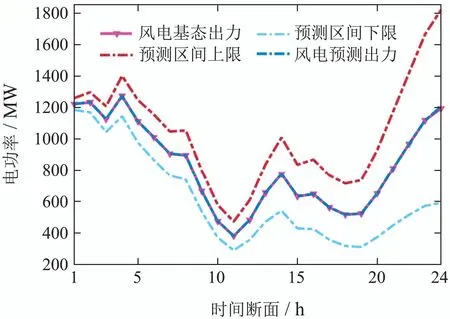
图3 场景1的风电出力概况图Fig.3 Diagram of wind power output in Scenario 1

图4 场景1的机组和P2G出力概况图Fig.4 Diagram of generator and P2G power output in Scenario 1

在场景2和场景3的鲁棒调度中，均考虑AGC机组和P2G装置追踪风电波动，其风电和机组出力情况分别如图5-6和图7-8所示.

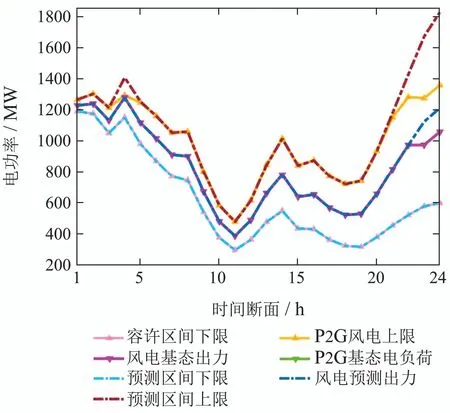
图5 场景2的风电出力概况图Fig.5 Diagram of wind power output in Scenario 2

图6 场景3的风电出力概况图Fig.6 Diagram of wind power output in Scenario 3

图7 场景2的机组及P2G出力概况图Fig.7 Diagram of generator and P2G power output in Scenario 2

图8 场景3的机组及P2G出力概况图Fig.8 Diagram of generator and P2G power output in Scenario 3

由图5和图6可知，场景2和场景3的风电基态出力曲线在时段23-24不能完全贴合于预测出力曲线.将场景2的AGC机组基态出力与其应对风电负、正波动的备用容量相加、相减的机组出力和的与场景3中的AGC机组出力容许上、下限称为AGC机组应对风电波动的鲁棒上限和鲁棒下限，以及场景2中的P2G装置基态出力与其应对风电正波动的备用容量相加的出力和场景3中的P2G装置出力容许上限统一称为P2G装置应对风电波动的鲁棒上限，并将上述鲁棒上、下限曲线反映在图7-8中，由此可知相比于场景1，场景2和场景3趋向于提高燃气机组和AGC燃煤机组的基态出力，在留有足够的风电负波动鲁棒备用容量的前提下，留有一定的风电正波动鲁棒备用容量，即在保证完全追踪风电预测区间下限的前提下，尽力追踪风电预测区间上限:在风电预测区间上下限相差较大的时段23-24，由于AGC机组的鲁棒备用容量有限，系统趋向于压低风电基态出力，以减小系统日后所需应对的最大风电向下波动，进而在基态下产生弃风.

由表1的数据可知，由于场景2和场景3中燃气机组基态出力高于场景1，进而造成鲁棒调度的基态供能总成本高于传统确定性调度;而由于场景1在日前没有给AGC机组分配合理的备用容量和优化机组的风电承担系数，限制了其在日后应对风电波动的调节能力，因而对比于场景2和场景3，场景1在日后蒙特卡洛模拟的极端风电出力场景中产生更多的弃负荷，造成其日后校正成本高于场景2和场景3，进而造成其实际调度成本高于场景2和场景3.由此可见，相较于传统的确定性调度，场景2和场景3对于风电波动具有明显的鲁棒性.

进一步由表1的数据可知，场景2在日后校正的过程的中产生了弃负荷，而场景3并不会产生弃负荷，这是因为:场景2基于AARO的IEGS鲁棒调度旨在最小化风电在区间内波动时所带来的最大功率缺额，因而场景2 的优化过程并不会遍历区间内的所有风电波动情况:而场景3的鲁棒区间调度旨在最大化区间的同时，保证风电在区间内波动时都不会出现功率缺额.因此，场景3的日前调度结果更为保守，其基态供能成本高于场景2，但场景3在日后校正过程中能够保证极端情况下不发生弃负荷.同时，对比图7和图8可知，在时段1-3场景3趋向于将应对风电正波动的备用容量转移给AGC燃煤机组，而场景2中则趋向于转移给P2G装置，这一区别导致在日后校正过程中场景2 的P2G 校正成本高于场景3，最终导致其实际调度成本高于场景3.由此可见，对比于场景2 的AARO调度，场景3的鲁棒区间调度日前调度的基态成本虽然较高，但其能够严格保证调度策略的鲁棒性，且更为合理地分配AGC机组和P2G装置应对风电波动的备用容量，以降低其在日后校正过程中的调整成本.

4.1.2 调节状态气网约束的必要性分析

场景4的鲁棒区间调度在场景3的基础上忽略了两种调节状态下的气网约束，其风电和机组出力情况如图9和图10所示.

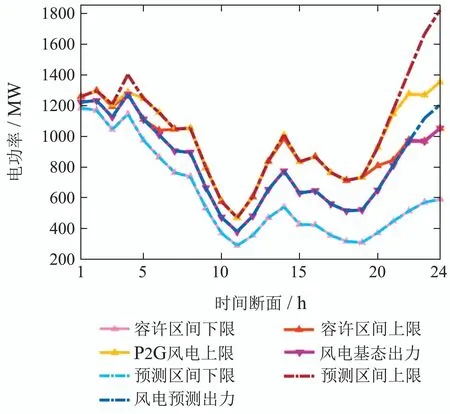
图9 场景4的风电出力概况图Fig.9 Diagram of wind power output in Scenario 4

图10 场景4的机组出力概况图Fig.10 Diagram of generator power output in Scenario 4

由图9可知，对比于场景3，场景4的风电基态出力曲线和容许区间下限曲线与场景3保持一致，但其容许区间上限曲线在时段14-16完全贴合于预测区间上限曲线，即场景4在时段14-16的风电容许区间大于场景3.

由图10可进一步分析场景4风电容许区间增大的原因:由于场景4忽略了调节状态下的气网约束，系统高估了气网调节资源在最大耗气量调节状态下的调节能力，因此拉高了燃气机组出力的鲁棒上限，进而在时段14-16将追踪风电预测区间下限的风电负波动鲁棒备用容量过多地分配给了燃气机组，对比图8可知，场景4中燃气机组应对风电负波动的鲁棒备用容量明显多于场景3;同时由于燃气机组承担了较多的风电负波动鲁棒备用容量，AGC燃煤机组无需通过压低基态出力而留出过多的风电负波动鲁棒备用容量，因而AGC燃煤机组同样可以提供足够的风电正波动鲁棒备用容量，进而压低P2G应对风电正波动的备用容量，最终导致了场景4的AGC机组在时段14-16能够追踪风电预测区间的上限.

根据以上分析可知，由于AGC机组在日前备用容量的配置成本低于P2G装置，场景4在日前对气网调节能力的高估将导致其趋向于将大部分应对风电正波动的备用容量分配给AGC机组，虽然这样能够降低日前的基态供能成本，但其在日后必然需要通过更大幅度的校正过程来纠正日前对气网调节能力的误判.进一步分析表1中数据可知，场景4的气网校正成本高于场景3，最后导致其实际调度成本高于场景3.由此可见，在IEGS鲁棒区间日前调度中考虑调节状态的气网约束，可以减少在日后的校正成本，充分体现其经济性.

5 结论

本文基于风电出力的预测区间建立了IEGS鲁棒区间调度模型，并基于IEEE 39节点电力网络和比利时20节点天然气网络搭建仿真模型验证了算法的可行性与有效性，进而得出以下结论:

1) IEGS鲁棒区间调度的基态供能成本虽然高于传统确定性调度，但其调度策略所得到的风电允许出力区间能够使系统在实时调度中较好地应对风电波动，在减少弃风的同时降低系统校正成本.

2) IEGS鲁棒区间调度的日前调度结果虽然比现有基于AARO的鲁棒调度更为保守，但其调度策略能够严格保证在风电在可消纳区间内波动时不产生弃负荷，并且更为合理地分配AGC 机组和P2G装置应对风电波动的备用容量，以减小日后的校正成本.

3) 由于气网的供气量存在一定范围，系统未必能够提供足够的天然气给燃气机组进行AGC 调节，因此在IEGS鲁棒区间调度模型中考虑调节状态下的气网约束，可以使IEGS在应对风电波动时得以考虑到对气网运行的影响，使调度决策更符合系统实际运行情况，以减小日后的校正成本.

附录A仿真算例参数

图A1 IEGS仿真拓扑图Fig.A1 Simulated topology diagram of IEGS

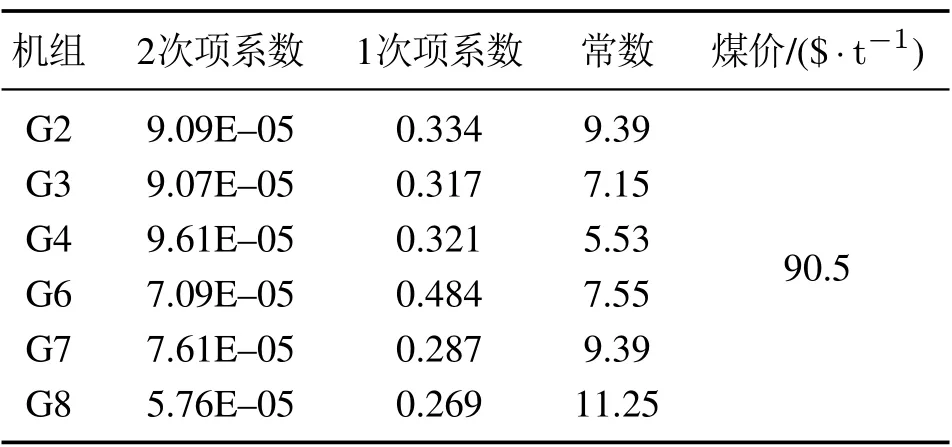
表A1 燃煤机组煤耗系数(t/MWh)Table A1 Fuel consumption coefficients of coal-fired generators(t/MWh)

表A2 燃煤机组出力参数Table A2 Output parameters of coal-fired generator

表A3 燃气机组参数Table A3 Parameters of gas-fired generator

表A4 电网负荷预测数据(MW)Table A4 Forecasted data of grid load(MW)

表A5 风电场1预测出力区间(MW)Table A5 Forecasted power output of wind farm 1(MW)

表A6 风电场2预测出力区间(MW)Table A6 Forecasted power output of wind farm 2(MW)

表A7 气源参数Table A7 Parameters of gas sources

表A8 储气库参数Table A8 Parameters of gas storages

表A9 P2G装置参数Table A9 Parameters of P2G device

表A10 罚凸凹过程初始化参数Table A10 Initial parameters of penalty convex-concave process

附录B IEGS的日后校正模型以最小化校正成本作为优化目标:

式中:不带上标“∧”的均为日前调度所求解的基态变量;dn，di，dj，m1，m2分别为AGC燃煤机组出力调整成本、P2G调整成本、气源出力调整成本、弃风成本以及弃负荷成本;为进入校正模型后的风电实际可用出力;dn=30$/MWh;di=1$/(Mm3·s-1);dj=0.25$/(Mm3·s-1);m1=100$/MWh;m2=5000$/MWh.

5种算例场景下校正模型的共同约束条件:

上述约束条件分别为:功率平衡、风电实际出力、负荷实际值上下限、机组实际出力、旋转备用、P2G实际耗电量以及气网约束条件.其中，分别为应对风电场k出力波动和负荷节点a产生切负荷后机组n所承担的功率不平衡量，为当风电场k实际可用出力大于容许区间上限时P2G装置i 所承担的功率不平衡量.另外，共同的约束条件还包括耗量特性、机组实际出力上下限、机组爬坡和潮流断面上下限约束，在此不一一列出.

1) 对于场景1的确定性调度，在进入校正模型后，其弃风量为目标函数中的弃风项，弃风量和机组应对风电波动的和再调整出力均为变量，存在