具有抗毁性的无线传感器网络有向拓扑模型

刘浩然，王星淇，覃玉华，邓玉静，尹荣荣

(燕山大学信息科学与工程学院，河北秦皇岛 066004;燕山大学河北省特种光纤与光纤传感重点实验室，河北秦皇岛 066004)

1 引言

无线传感器网络(wireless sensor networks，WSNs)是由大量微型传感器节点通过无线通信的方式，自组织形成的一个多跳分布式网络系统.目前应用于环境监测[1]、军事侦察[2]、智能交通网络[3]、电力网络[4]和物流配送网络[5]等领域，有着广泛的应用前景.网络抗毁性[6]是指当网络受到选择性或随机性攻击时，网络维持或恢复其性能到一个可接受程度的能力，作为WSNs的一种重要特性，其理论意义和应用价值日益受到人们的关注和重视.如何构建具有良好抗毁性的有向无标度网络拓扑，成为WSNs面临的一个重要挑战.目前，对于WSNs抗毁性拓扑的研究，大多建立在经典无标度BA(Albert-László Barabási and Réka Albert)模型基础上[7]，通过引入抗毁性相关参数因素，达到提高网络抗毁性的目的.文献[8]借助节点批量到达的Poisson网络模型，提出了一种WSNs无标度容侵优化拓扑(scale-free intrusion-tolerance optimization topology，SIOT)模型，通过优化拓扑中的幂律指数提高网络容侵性.文献[9]通过减少网络度分布的程度，建立了理论模型增加系统在恶意攻击和随机攻击下相关网络的抗毁性.文献[10]在添加连接链路的基础上提出一种辅助优先附件策略，提高了相互依赖网络的鲁棒性.文献[11]基于最短路径，通过合理分配有限成本，添加连接链路和依赖链路，所构建拓扑比只添加连接链路或依赖链路具有更强的抗毁性.文献[8-11]多是从节点度或介数中心性相关理论角度提出策略或生成拓扑进行研究，虽然均在一定程度上提升了WSN的抗毁性，但是考虑角度比较单一，在优化网络抗毁性上仍存在局限性，且添加连接链路的方式大大增加了计算连接条件的复杂度，难以应用于工程实践.文献[12]结合路径中心性和节点度，提出路径算子演化中心(path operator calculus centrality，POCC)，一定程度上提高了网络的能耗和性能.文献[13]从节点度和介数中心性两方面建立了无标度网络的鲁棒性模型，有效地增强了无标度网络对级联失效的抗毁性.上述文献虽从不同角度对网络抗毁性进行大量研究，但均未考虑实际数据传输过程中的有向性.为了将WSNs相关理论更广泛地应用到人类生产生活和实践当中，许多学者对有向网络的研究进行了一系列深入探索，文献[14]通过引入了一种定量标准来描述有向网络社区，并利用马尔可夫链蒙特卡洛(Markov chain Monte Carlo，MCMC)随机搜索技术优化有向局部社区结构，同时提高其抗毁性.文献[15]利用等价变换和相关划分，研究了有向加权符号网络(multiagent system，MAS)的能控性和稳定性.文献[16]同时考虑了单向拓扑和双向拓扑，证明了在联合强连通和无线联合连通时，网络的一致性问题.虽然文献[14-16]对有向网络相关问题进行了探索，但对抗毁性的研究不够深入，更没有在全局性和局域性角度全面考虑提升抗毁性的因素.而实际应用中，有向网络承受恶意攻击的能力对于网络持续有效地运行有着至关重要的作用.

基于以上分析，本文结合节点出入度和介数中心性两种抗毁性因素，同时考虑网络数据传输过程中的有向性，以提高有向网络面对不同攻击方式的抗毁性为目标，构建了可以衡量网络抗毁性的抗毁性度量模型.继而将其引入节点择优连接概率中，构建了具有抗毁性的有向传感网络拓扑模型(destruction resistant topology model of directed sensing network，DRTD)，并通过理论和仿真证明通过本文方法构建的拓扑模型具有强抗毁性.

2 抗毁性度量模型

WSNs网络抗毁性是指当网络中的节点或边发生故障或遭受攻击时，网络拓扑结构保持连通的能力[17].本节从全局性和局域性角度出发，结合基于最短路径数的介数中心性及节点自身特性的节点出入度两种因素，构建抗毁性度量模型，衡量节点的重要性及其对网络抗毁性的影响程度，公式为

其中:i为节点编号，A表示邻居节点的集合.为全局抗毁因子，由单独节点和总体介数中心性的比值构成.介数中心性是衡量节点重要性的指标之一，其定义为网络中所有最短路径中经过某一节点的路径数目在最短路径总数中占有的比例[18]，它体现了节点传输数据时可选择路径的多少.对于有向网络，数据沿着不同方向传输时，最短路径也会改变，导致节点传出数据时的介数中心性BCi(out)和接收数据时的介数中心性BCi(in)不相等，二者分别表示用经过节点的出度路径数目和入度路径数目刻画该节点重要性的指标.在数据传输过程中，节点之间是否有可选择的冗余链路是网络具有抗毁性的主要原因.因此，介数中心性反映了相应的节点在整个网络中的作用和影响力，参考文献[18]中的定义，介数中心性的公式为

其中:n为网络节点数;σkt(i)为节点k到节点t的最短路径经过节点i的次数;σkt为节点k和节点t之间最短路径数.最短路径是网络中节点数据传输的重要途径，在网络面临攻击和破坏的情况时，最短路径数越多，数据传输途径的选择越多，网络抗毁性越强.因此节点间最短路径数对于提升网络抗毁性有着重要意义[19].

由式(1)可知，抗毁性度量值与节点的介数中心性和节点度的变化呈正比关系.当网络不够均匀时，处于重要位置的度大节点较少，绝大多数节点的抗毁性度量值过小甚至趋于零，网络面对选择性攻击的抗毁性较差;反之，当网络足够均匀时，节点之间互异性较小，抗毁性度量值大的重要节点较多，网络面对选择性攻击的抗毁性较强.

3 抗毁性有向网络模型拓扑及动态特性分析

假设节点均匀部署在无线传感器网络中.为了获取具有抗毁性的有向拓扑模型，解决有向WSNs面对不同攻击方式时抗毁性较差的问题，将抗毁性度量模型引入到WSNs拓扑节点的出入边择优连接概率中，演化生成出具有抗毁性的有向网络拓扑结构，并对其进行动态特性分析.

3.1 DRTD演化模型

由于网络中节点的通信半径有限，当有新的节点加入到网络时，在只考虑局部信息的情况下，通过对其进行择优连接来构建局域世界.再根据节点总是将接收到的数据向sink节点传播这一方向性，结合无标度理论，将节点发送与接收时的抗毁性度量分别引入到节点出边和入边择优连接过程中.类似于经典BA模型，同样将DRTD算法分为增长和择优连接两部分，构建的演化模型具体描述如下:

1) 增长:由m0个节点，e0条有向边任意相连而组成的初始网络.在每个时间步长内，新加入的节点new与网络中已存在的m ＜m0个节点相连，形成新的有向网络.

2) 有向局域世界择优连接:新节点new的M1个邻居组成它的出度局域世界，用A1表示;M2个邻居组成它的入度局域世界，用A2表示，同时引入参数p∈[0，1].

节点和边的增长规律遵循以下原则:

①pm条有向边将新节点new与网络中的已存在的pm个节点相连，连接概率与当前节点的介数中心性和出度有关，边的方向都是从节点new指向己经存在的节点.该节点i被选择的概率为

②其余的(1-p)m条有向边与网络中剩下的(1-p)m个节点相连，边的方向都是从网络中已经存在的节点指向新节点new.该节点i被选择的概率为

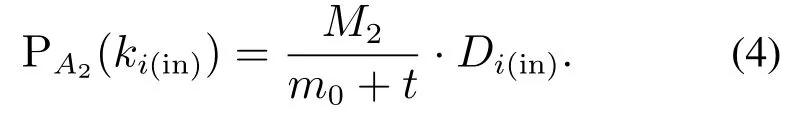
经过t时间步后，将形成一个具有N=m0+t个节点，mt+e0条有向边的无标度网络.

从DRTD演化模型可以看出，节点在进行择优连接时，同时考虑了全局抗毁因子和局域抗毁因子两种因素.下面通过对DRTD演化模型动态性能进行分析，分别得到拓扑的出度和入度的度分布表达式.

3.2 DRTD模型动态特性分析

借助Mean-Field理论来分析有向网络中出度和入度的度分布，解析得到网络中节点的出度和入度随时间的分布情况.假设新节点new在t时刻加入网络(如图1所示)，R0为初始时刻网络半径，R0+t为t时刻的网络半径，Rnew为新加入new节点的通信半径.具体情况见图1.

图1 模型有向组网示意图Fig.1 Schematic diagram of model directed networking

因监测区域内节点部署服从均匀分布，选择新节点new的邻节点集的概率可由节点new覆盖区域的面积与t时刻网络区域的面积比来近似，则首先对于节点出度的节点度分析为

由于网络中的节点均匀分布，新节点new局部区域内节点出度的总和可表示为

其中:N(t)为t时刻网络中的总出节点数;ki(out)为网络中节点的平均节点出度.

将式(6)和式(7)代入式(5)得

其中f(BCi(out))=.借助连续性和连续场理论，可通过平均场近似方法求得算法中节点出度同时间的演化关系.假设节点k是连续变化的，则ki(out)连续变化的速率可以表示为

求解该微分方程可得

其中:ki(out)(t)为t时刻节点i的出度;C为常数.将初始变化条件ki(in)(t)=m代入式(10)，解得常数C:

到节点i的节点出度随时间变化的规律为

节点i的出度小于k的概率P(ki(out)(t)＜k)可由下式求得:

由于在择优增长过程中，ti服从均匀分布，其概率密度满足如下条件p(ti)=，代入式(13)可得节点出度分布P(ki(out))的表达式为

同理，对节点入度进行节点度分析得到节点入度分布P(ki(in))的表达式为

由式(14)和式(15)可以看出，演化生成的有向无标度拓扑，其出度和入度均服从幂律分布，分布的幂率指数为γ=，因此上述的分析结果表明由DRTD模型生成的拓扑具有无标度特性.

4 仿真分析

通过MATLAB软件对DRTD模型进行实验仿真.为了明确通过抗毁性度量模型衡量网络抗毁性的正确性和所构拓扑网络自身的抗毁性，首先对模型自身的网络度分布及抗毁性度量进行仿真，实验环境参数见表1;其次在最大连通分支比例和网络效率两方面对DRTD拓扑模型和文献[8]、文献[10]、文献[12]模型进行对比分析，验证所提出模型的优越性.同时，为了较好的研究不同算法的性能差异，在4种算法运行之初规定相同的网络规模，并假设拥有相同的初始节点链接，数据结果均取50次实验的平均值.

表1 实验环境参数Table 1 Experimental environment parameters

4.1 DRTD模型动态特性分析

节点按照均值为λ 的泊松分布随机部署在500 m×500 m的方形区域中[21]，节点数目设为100个，依据表1所示实验参数，演化出了本文所构建的具有抗毁性的有向网络拓扑结构，如图2所示.

图2 网络拓朴结构Fig.2 Network topology structure

图2中:黑色箭头表示出边，即网络数据从其他节点向该节点传输;灰色箭头表示入边，即网络数据从该节点向其他邻居节点传输.从图中可以看出，该算法生成的有向网络拓扑结构均匀，拥有少量居于重要位置且度较大的关键节点，例如80号节点、82号节点和99号节点等，且簇与簇之间同样有连接，与理论分析结果一致.

4.2 节点出入度分布分析

网络拓扑节点的出度和入度度分布如图3所示.

图3 网络节点出入度度分布Fig.3 Network node access degree distribution

从图3中可看出，本文所构DRTD演化模型生成的有向网中的节点出度和入度度分布均近似服从幂律分布，遵循了形成无标度拓扑的必要条件，满足无标度的网络特征，与理论分析结果一致.

4.3 网络抗毁性效果分析

根据本文所提出的的网络抗毁性度量计算公式，分别对网络抗毁性度量随介数中心性及节点度而变化的趋势和各个节点的抗毁性度量值进行仿真.仿真效果如图4所示.

图4 抗毁性度量值效果图Fig.4 Effect diagram of damage resistance measurement value

根据图4可看出，网络抗毁性度量随着节点介数和度的增加呈正幂次递增趋势.网络中拥有少量介数和节点度较大的关键节点，大量的介数和节点度较小的小度节点.从节点重要性分布角度观察，有助于提高网络抗毁性.

4.4 最大连通分支比例对比

为了分析不同算法下的网络对节点失效规模的容忍程度，衡量DRTD算法形成拓扑的抗毁性，将此模型同上文所提3种模型进行对比仿真，分别统计随机移除和选择性移除节点后网络的最大连通分支比例.本实验中，最大连通分支比例定义为当网络中的失效节点被移除时，剩余网络各连通分支存活节点数总和同网络总节点数的比值，如图5-6所示.

图5 随机移除情况下最大连通分支比例对比图Fig.5 Comparison of the maximum connected branch ratio under random removal

从图5中可看出，4种模型在面对随机移除时均表现出一定的抗毁性能，这是因为它们的建立均基于无标度演化规则，拓扑中度小的节点数量较多，移除并失效的概率偏大，而度小节点的失效往往不会严重影响网络的连通性.随着随机移除比例不断增大，DRTD模型最大连通分支比例始终高于其他3种模型.这是由于在择优连接时，DRTD模型考虑到节点自身介数和节点度，有关因素的全面分析使得对连接节点的选择更合理，有助于增强网络的健壮性，相当于其他3种模型，也表现出更强的抗毁性.

从图6中可看出，网络最大连通分支比例随着选择性移除比例的增大而迅速降低.但相比其他3种模型，DRTD模型所构建网络连通性的损坏程度较低，表现出更强的抗毁性.当重要节点遭受选择性攻击并被移除时，影响的节点范围增大，连接节点数大量减少，网络连通性迅速下降.当选择性移除比例达到0.12%时，其他3种模型的最大连通分支比例降为0，而DRTD模型仍达到近0.1%.这是因为DRTD模型在节点之间连接的概率因素中考虑了全局性和局域性因素，通过最短路径数所获得的介数中心性和节点度以更加合理的比重将连接链路分配给节点，因此所构拓扑相对于其他3种模型更加稳定，也表现出更好的抗毁性.

图6 选择性移除情况下最大连通分支比例对比图Fig.6 Comparison of the maximum connected branch ratio under selective removal

4.5 网络效率对比

为了更好地反映出无标度网络在面临部分节点失效时，连通分支尺寸从大到小的演化过程，本文又针对不同模式的节点失效状态下网络效率E的变化进行对比仿真.网络效率公式为E=其中dij为任意两点间最短距离的跳数.在节点失效后，E值保持越大，表明网络抗毁性越好，并且有E∈(0，1]，其中，E=0对应全孤立点网络，E=1对应全局耦合网络.仿真结果如图7所示.

从图7可看出，本文所提出的DRTD模型的网络效率E相较于其他3种模型初始值较高，在随机移除和选择性失效情况均有优势.例如，在随机节点失效达到较高的0.2%时，DRTD模型网络效率达到0.05%，而其他3种模型在0.04%以下;在选择性失效情况下，DRTD 模型曲线更为平缓，网络效率下降速度较为缓慢，在失效比例达到0.3%时仍处于对比模型中最高的一种.

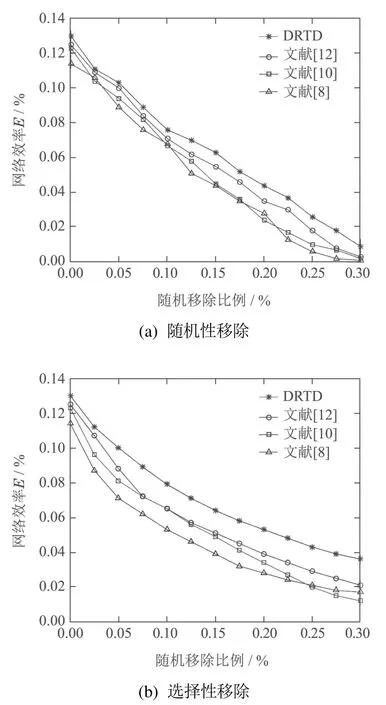
图7 网络效率随节点失效比例变化图Fig.7 Network efficiency changes with node failure ratio

由上述实验分析可得，由DRTD模型所建立的有向无标度网络拓扑对于网络遭受攻击，特别是选择性攻击时，表现出更加优越的抗毁性能，节点之间的连接更为稳定，网络变得更均匀化.同时比较文献[12]与其他两种只考虑单一因素的算法，也证明了本文算法考虑角度的正确性.DRTD模型更符合WSNs拓扑的演化规则，更符合实际应用的要求.

5 结论

本文在深入研究无线传感网络抗毁性的基础上，提出了一种结合节点出入度和介数中心性两种抗毁性因素的有向传感网络拓扑模型DRTD.通过动态性能分析，证明了该拓扑中节点出度和入度均服从幂律分布，符合无标度特性.仿真结果表明，通过该算法生成的有向拓扑网络中，抗毁性度量值随节点出入度和介数中心性的增大而呈正幂次递增趋势.当面对选择性攻击和蓄意攻击时，同文献[8]、文献[10]、文献[12]3种不同模型相比，DRTD模型的最大联通分支比例和网络效率在下降速率和网络崩溃临界值上，都表现出更好的抗毁性，为研究有向无线传感器网络提供了新思路.