直线与圆锥曲线

一、填空题

1.若过点（-2，0）的直线l与双曲线C的方程为有且仅有一个公共点，则满足条件的直线的条数为.

3.过点P（-1，1）作直线交椭圆=1于A，B两点，若线段AB的中点恰为P，则AB所在直线的方程为________.

5.设抛物线C：y2=4x的焦点为F，过点（-2，0）且斜率为的直线与C交于M，N两点，则________.

6.若斜率为1的直线l与椭圆1相交于A，B两点，则AB的最大值为________.

7.已知抛物线C：y2=8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若，则QF=________.

8.如图，已知C，B分别是椭圆E：=1的上，下顶点，F是它的左焦点，点M为线段BC（包括端点）上的一个动点，射线MF交椭圆于点N，若向量则λ的取值范围是________.

（第8题）

二、解答题

（1）若以原点为圆心，椭圆短半轴长为半径的圆与直线y=x+2相切，求椭圆的焦点坐标；

（2）若点P是椭圆C上的任意一点，过原点的直线l与椭圆交于M，N两点，直线PM，PN的斜率的乘积为，求椭圆的方程.

10.在平面直角坐标系xOy中，椭圆C：的右准线方程为x=4，右顶点为A，上顶点为B，右焦点为F，斜率为2的直线l经过点A，且点F到直线l的距离为.

（1）求椭圆C的标准方程.

（2）将直线l绕点A旋转，它与椭圆C相交于另一点P，当B，F，P三点共线时，试确定直线l的斜率.

11.已知抛物线C的顶点为O（0，0），焦点为F（0，1）.

（1）求抛物线C的方程；

（2）过点F作直线交抛物线C于A，B两点.若直线AO，BO分别交直线l：y=x-2于M，N两点，求MN的最小值.

（第11题）

（1）求椭圆C的方程；

（2）若不过点A的动直线l与椭圆C相交于P、Q两点，且求证：直线l过定点，并求出该定点N的坐标.

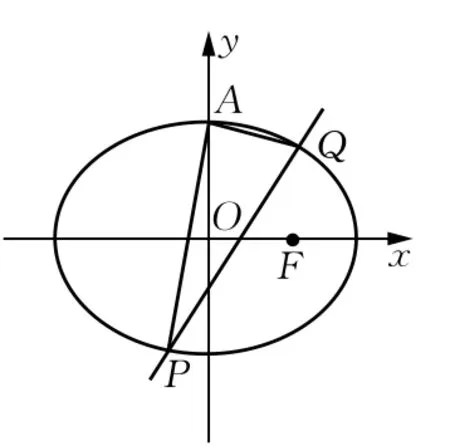
（第12题）

三、挑战高考（2019年江苏卷第17题）

13.如图，在平面直角坐标系xOy中，椭圆的焦点为F1（-1，0），F2（1，0）.过F2作x轴的垂线l，在x轴的上方，l与圆F2：（x-1）2+y2=4a2交于点A，与椭圆C交于点D.连结AF1并延长交圆F2于点B，连结BF2交椭圆C于点E，连结DF1.已知.

（第13题）

（1）求椭圆C的标准方程；

（2）求点E的坐标.