认真审题，选择顺序，轻松解题——一道习题的解法及启示

邵一明

今天老师让我上黑板板书了一道习题，这是一道椭圆中直线求斜率的题目.老师看了我的板书后，表扬了我的解题方法，我很高兴.仔细想来，我在解题过程中有一些体会，与大家分享.

【问题呈现】

在平面直角坐标系中，椭圆C的右准线方程为x=4，右顶点为A，上顶点为B，右焦点为F，斜率为2的直线l经过A点，且点F到直线l的距离为.

（1）求椭圆的标准方程.

（2）将直线l绕点A旋转，它与椭圆C相交于另一点P，当B，F，P三点共线时，试确定l的斜率.

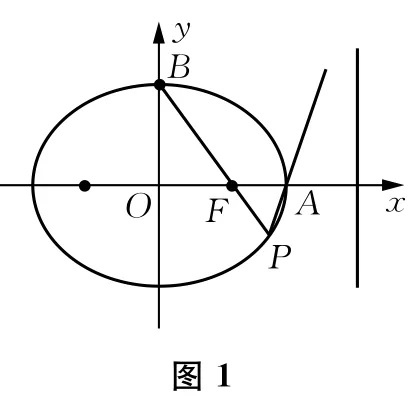
【解题经历】

●分●析 本题是一道比较简单的求椭圆方程和直线斜率的题目.题目看似简单，但我认为内涵丰富.第（1）问考查椭圆方程求法，属基础题，利用待定系数法易求出椭圆方程为.第（2）问，我一看到题目就想到先设直线l的方程，与椭圆方程联立，求点P的坐标，于是就有了如下解法：

●解●法●1 设直线方程为y=k（x-2），

代入椭圆方程，化简可得（3+4k2）x2-16k2x+（16k-12）=0，

因为B，F，P三点共线，又已知，

解题结束，回顾解题过程，我觉得很烦琐，想起数学老师每次讲完一道题总会问我们一句：“你们还有其他什么方法吗？”那这道题，除此解法，还会有什么简洁的方法吗？我仔细看了一眼插图，当看到B，F，P三点时，忽然想起“当B，F，P三点共线时”我豁然开朗，点B，F坐标是已知条件，lBF：显而易见，由此我想到了以下解法：

又因为A（2，0），所以.

图2

【反思感悟】

此题虽然不算太难，但我总认为能有多种解题方法的题目都不失为一种好题目.解题过程中，我还得出一些感悟：解题不要漏看题目中的插图，好的图形有助于打开解题思路.解题除了可以用常规思路求解，还要学会反思，在反思中提高数学思维能力，在反思中找到学习数学的乐趣.

【老师点评】

解析几何的运算是不少高中学生所惧怕的，这里既有题目的难易因素，也有做题的心理因素.邵一明同学在练习时能够沉着冷静，注意观察题目的条件和图形结构，选择了第二种方法，顺利解出了本题.从中同学们能够得到什么启发呢？

（邵一明，江苏省兴化中学高三（6）班；指导老师：徐永忠）

本期“牛刀小试”“真题练”参考答案

P9“真题练”：1.（1）2或6；（2）存在定点P（1，0），过程略.

P38“牛刀小试”：（1）1；（2）｛1｝；（3）略.

改编1：（1）｛x|-2≤x≤3｝；（2）（-∞，-6］∪［2，+∞）.