供水管网节点流量不确定性对漏损定位的影响

雷雨晴 杜坤 丁榕艺 毛润康 陈攀

摘 要：供水管网中的节点流量具有不确定性，为了研究节点流量不确定性对供水管网漏损定位能力的影响，建立供水管网节点流量分布在不同条件下的需求分布水力模型。一种是供水管网中各节点平均分配流入量的均匀模型，另一种是在供水管网各节点按需分配流入量的分配模型，比较两种需求分布模型的漏损定位性能。利用加权最小二乘算法完成供水管网水力模型的漏损定位，加权最小二乘算法具有模型精度高和计算效率高的优点，该方法通过计算供水管网中监测值与水力模型模拟值的差异，判断是否发生漏损，并能准确定位漏损节点。最后通过实例证明供水管网节点流量的不确定性对供水管网漏损定位性能有突出影响。

关键词：供水管网;节点流量;漏损定位;加权最小二乘法;蒙特卡罗算法

DOI： 10. 11907/rjdk.192295

开放科学（资源服务）标识码（OSID）：

中图分类号：TP319

文献标识码：A

文章编号：1672-7800（2020）001-0144-04

0 引言

供水管网作为城市重要基础设施，对于保障人类正常生活至关重要。供水管网在地下铺设纵横交错、范围遍布广、运行管理复杂、管道老化等因素极易造成供水管网漏损，供水能耗增大[1]。供水管网漏损浪费了珍贵的水资源，加大了企业供水成本，并且在一定程度上造成水质污染，还会降低居民生活品质。因此，及时定位供水管网漏损非常重要。

供水管网疏密不均、用水情况复杂，使得供水管网节点流量具有明显不确定性，研究节点流量不确定性对供水管网漏损定位造成的影响，对供水管网漏损定位和优化设计意义重大[2]。关于供水管网节点流量的不确定性，国内外许多专家学者对此展开研究。Lansey[3]等基于节点流量、节点压力、管段摩阻的随机性，在假定它们服从正态分布的情况下，提出了不确定性条件下供水管网优化设计方法，建立了机会约束模型并进行了求解;刘孟君[4]等利用一阶泰勒展开式导出的节点压力对节点流量的偏导矩阵，研究了节点流量不确定性对供水管网水力特性的影响，发现当节点流量变异系数较大时，所作的随机分析会产生较大误差;Kapelan[5]等在仅考虑节点流量不确定性的条件下，提出了一个随机优化设计模型，并用遗传算法进行了求解;常丽慧[6]等利用蒙特卡罗随机抽样法研究了节点流量和水损系数不确定性对供水管网节点测压管水头和管段流量的影响，得出节点测压管水头和管段流量计算方法。

目前，有关供水管网节点流量不确定性对管网水力特性的研究较多，但节点流量不确定性对供水管网漏损定位研究很少[7]。供水管网漏损定位利用需求分配细节设定需求分布模型，第一种是按管网中节点流量消耗比例分配的分解模型，另一种是管网中所有节点均匀分配流量的均匀模型。通过比较两种需求分布模型的漏损定位性能，进而研究供水管网节点流量不确定性在不同需求分布模型下对漏损定位的影响。

1 管网水力模型建立

当供水管网拓扑结构固定时，某一节点发生漏损，将会影响这一节点和供水管网其余节点的流量变化，Perez[8]等发现基于模型的方法适用于管网漏损定位问题。为了研究供水管网节点流量不确定性对漏损定位的影响，建立两种需求分布水力模型。第一个水力模型是在供水管网中所有节点平均分配流入量，称为均匀模型;第二个水力模型在供水管网节点分配不同的流入量，称为分解模型。其中，分配模型是根据每个节点用水量占供水管网总用水量比例设置管网内各节点的用水权从而分配用水量[9]。

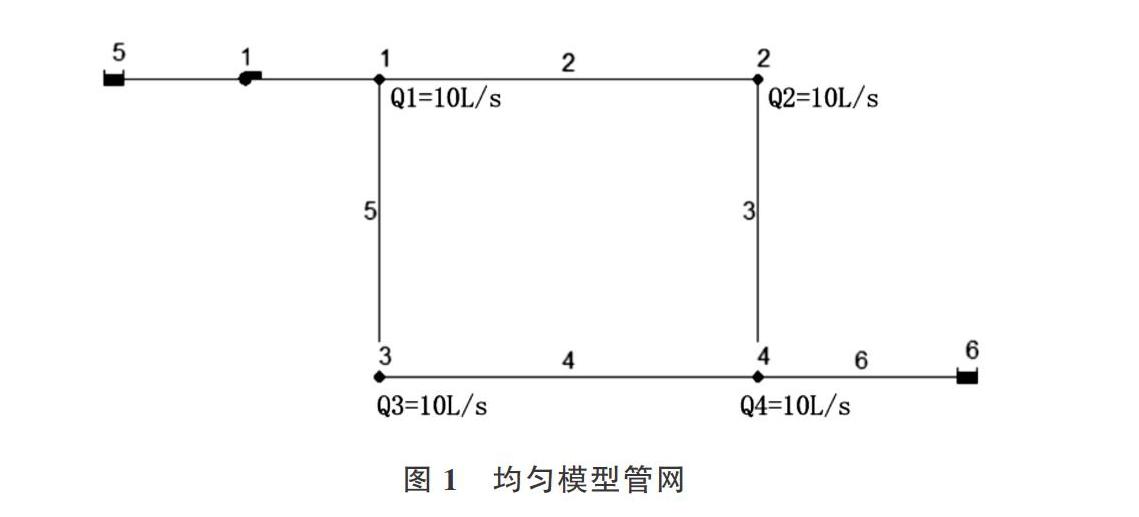
因此，可以利用这两种不同的需求分布水力模型，根据监测点信息，通过计算得出供水管网漏损位置。图1和图2为简单的供水管网拓扑结构，该供水管网是典型的环状管网，包括4个节点、1个高位水池、6根管段、1个水泵供水，入口处的流量测量使用特定需求分布（均匀或分解）分配给网络上的各节点。图1显示了供水管网均匀模型各用水节点平均分配流入量，图2显示了供水管网分配模型。

2 节点流量不确定性分析

运行供水管网时，因为管网中管段分布纵横交错导致了供水管网节点流量有着明显的不确定性[11]。节点流量不确定性会对供水管网的水力水质特性产生影响，对研究节点流量对供水管网漏损定位的影响具有重要意义[11]。

供水管網中的不确定性是一个概率问题，近年来节点流量对供水管网水力不确定性研究较多，在供水管网水力不确定性分析中应用最广的是蒙特卡洛模拟（Monte Carlomethod，MCS）。舒诗湖[12]等采用蒙特卡罗随机抽样法从输入精度方面分析了供水管网参数的不确定性。蒙特卡洛随机抽样法是关于随机变量的数值模拟方法，通过建立问题的概率分布模型，根据模型概率抽样得到一组随机数，重复抽样计算过程得出目标解[13]。

本文通过MCS算法分析供水管网节点流量不确定性，可以得到该管网节点流量的概率分布，从而量化节点流量不确定性的置信区间[14]。供水管网节点流量的不确定性边界可预警供水管网漏损事故，水务公司可及时采取相应策略以解决问题。实际供水管网中节点流量有着时空不确定性，因此研究节点流量对供水管网水力不确定性具有重要意义，同时能够为及时定位供水管网漏损事故提供便捷[20]。

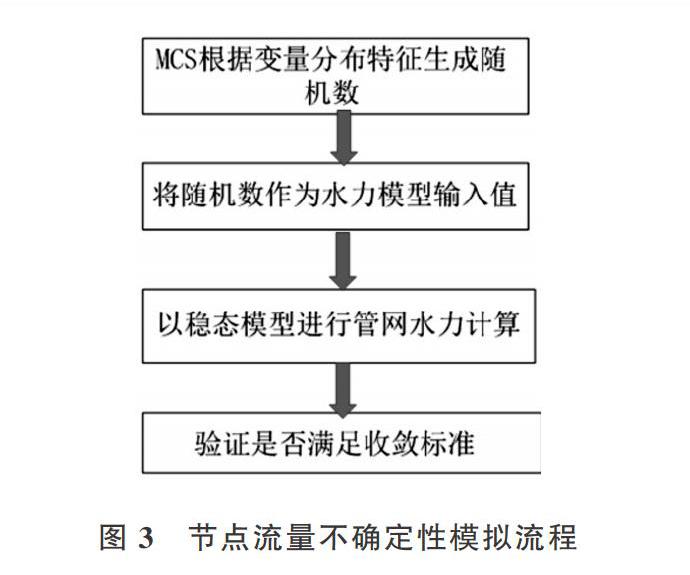
研究供水管网节点流量不确定性对供水管网漏损定位的影响，首先利用蒙特卡罗随机抽样法对供水管网节点流量的分布特征模拟生成仿真值，以随机数作为水力模型输入值，然后按稳态模型（连续性方程和动力学方程）进行管网模型水力计算，验证是否满足收敛标准[15]。节点流量不确定性模拟流程如图3所示。

3 供水管网漏损定位模型算法

通过加权最小化二乘误差平方和进行残差计算实现供水管网漏损定位的方法称为加权最小二乘法（ WeightedLeast Squares，WLS）。加权最小二乘法是梯度迭代算法的一种，具有参数设置简单且收敛速度快的优点[16]。WLS算法能够在拟合时对变化较小的测量值赋予较大权重，更好地提高模型精度，而且计算效率高，被广泛用于各类工程问题。Kang&Lansey[17]等用加权最小二乘法校核了供水管网节点流量和管道阻力系数，并用随机取样法估计了节点流量的波动范围，可以对供水管网中可能发生的漏损事故作出预警。供水管网漏损会影响供水管网流量监测值范围，通过构建供水管网水力模型，供水管网漏损定位问题可以用WLS算法解决[18]。该方法是计算供水管网中监测值与水力模型模拟值的差异，残值大于临界值则进行漏损预警，并且建立目标函数，利用加权最小二乘回归分析，比较目标函数残差值，残差值越小，即为供水管网漏损点[19]。

考虑供水管网中每个变量观测数据的误差分布不同，一般定义加权目标函数为：

4 管网漏损定位

为探究供水管网节点流量不确定性对漏损定位影响，对两个需求分布水力模型进行模拟，观察其漏损定位性能表现。

利用WLS算法求解供水管网漏损定位问题的目标函数为：

选用图1和图2中的两个小管网作为例子，这两个管网除节点流量分布外基本一致。假设管网中节点2、3、4顺序漏損，同时赋予其不同的节点漏损量进行模拟，找到观测值与模拟值误差最小的点即为管网漏损点。管网中各管道的管长均为150m，管径均为75mm，海澄威廉系数均为90。利用Matlab对WLS算法进行编程得到的目标函数节点流量残差如图5所示。

图5给出了均匀模型和分解模型在节点2和节点4时发生漏损，并针对不同漏损量计算得出的目标函数残差。可以看出，当管网中某一节点发生漏损时，由供水管网节点流量不确定性引起的两种需求分布水力模型计算得到的残差不同，均匀模型计算出的残差值远大于分解模型计算出的残差值，并且随着漏损量变大，虽然两种模型残差值都在减小，但分解模型的残差值更加趋近于零。由此可见，模拟相同漏损情况下分解模型较均匀模型在供水管网漏损定位方面更为高效。

5 结语

为了研究在供水管网中节点流量不确定性对漏损定位的影响，通过在水力模型中设置两种不同的流量分布得到分解模型和均匀模型，运行两种模型后，分解模型较均匀模型产生了更好的结果。研究发现，供水管网定位漏损时使用分解模型对供水管网漏损定位更为高效。由于供水管网漏损定位不仅取决于水力模型建模方法，还取决于供水管网中测量设备的实际位置。未来将重点研究传感器设备放置策略对实际供水管网漏损定位的影响。

参考文献：

[1]舒诗湖，何文杰，赵明，等.供水管网漏失检测技术现状与进展[J].给水排水.2008（6）：114-116.

[2]刘书明，王欢欢，徐锦华，等.基于智能优化算法的供水管网漏水点 定位[J].同济大学学报（自然科学版），2014，42（5）：740-744.

[3]KAPELAN Z. SAVIC D， WALTERS G A. Robust least cost design ofwater distribution systems using GAs[C].International Conference onComputing and Control for the Water Industry' London. 2003.

[4]BABAYAN A V. SAVIC D A，WALTERS G A.Multiobjective optimi-zation of water distribution system design under uncertain demand and pipe roughness[C].Venice： Impacts of Global Climate Change， 2005.

[5] 刘孟君，邹平华，何钟怡.供水管网中节点流量随机性的影响分析[J].给水排水，2007. 33（ zl）：350-354.

[6]BOULOS P F，ORMSBEE L E.Explicit network calibration for multi-ple loading conditions[J]. Civ. Eng. Syst.， 1991，8（3）：153-160.

[7]KAPELAN Z S，SAVIC，D A， WALTERS G A.Calibration of water dis-tribution hydraulic models using a Bayesian-type procedure[J].Jour-nal of Hydraulic Engineering， 2007（8）：927-936.

[8]吴学伟.赵洪宾.给水管网状态估计方法的研究[J].哈尔滨建筑大学学报，1995，28（6）：60-64.

[9] 范江，杜坤.基于加权最小二乘法的供水管网节点流量校核[J].土木建筑与环境工程，2016， 38（3）：73-79.

[10]ZHENG， FEIFEI. Noncrossover dither creeping mutation-based ge-netic algorithm for pipe network optimization [J]. Journal of Water Resources Planning and Management ， 2014 ， 140（ 4） ： 553-557.

[11]YU S， SHIPENG C . ZHANG T Q ， et al.A greedy sampling design al-gorithm for the modal calihration of nodal demand in water distribu- tion systems[J] . Mathematical Problems in Engineering， 2019 ： 1-1 1.

[12]SEIFOLLAHI-ACHMIUNl S. BOZORG HADDAD 0 ， OMID M H ， et aI.Effects of pipe roughness uncertainty on water distribution net- work performance during its operational period [ J] . Water ResourcesManagement， 2013 ， 27（ 5 ） ： 1581-1599.

[13]PILLER O.Modeling the behavior of a network-Hydraulic analy-sis and sampling procedures for parameter estimation [ D ] . BordeauxCedex ： Univ.of Bordeaux， 1995.

[14]杜坤，供水管网水力模型校核与损定位研究[D]，重庆：重庆大学 ， 2014.

[15]DI NARDO A. DI NATALE M. GISONNI C. et al. A genetic algo-rithm for demand pattern and leakage estimation in a water distribu-tion network [Jl. Water Supply ： Res. Technol. -Aqua， 2015 ， 64（ 1 ） ， 35-46.

[16]BEAL C . STEWART R.ldentifying residential water end uses under-pinning peak day and peak hour demand [DB/OL]. Water Resour.Plann. Manage. ， 10.1061/（ ASCE ） WR.1943-5452.0000357 . 04014008 ， 2014.

[17 ]赵洪宾.供水管网水力、水质型校核标准探讨 [ J ] .给水排国水. 2008，24（ 18）. 104-106.

[18] GOLDBERC D E， DEB K. A comparative analysis of selectionschemes used in genetic algorithms [ J] . Foundations of genetic algo- rithms[ J] . Foundations of Cenetic Algorithms . 1991 （ l ） ： 69-93.

[19] GOLDBERC D E. Cenetic algorithms in search， optimization andmachine learning [Ml. Menlo Park： Addison-Wesley Longman， 1989.

[ 20]NHU DO ， ANGUS SIMPSON ， JOCHEN DEUERLEIN ， et al. Demandestimation in water distribution systems： solving underdeterminedproblems using genetic algorithms [ C ] . In XVIII International Confer-ence on Water Distribution Svstems . WDSA2016. 2017 ： 193-201.

（責任编辑 ：孙娟 ）

基金项目：国家自然科学基金项目（ 51608242）;云南省应用基础研究青年项目（2017FD094）

作者简介：雷雨晴（1995-），女，昆明理工大学建筑工程学院硕士研究生，研究方向为市政工程;杜坤（1986-），男，博士，昆明理工大学建筑工程学院讲师，研究方向为市政工程。本文通讯作者：杜坤。