多媒体信息技术辅助中职数学的教学探讨

陈燕凤

【摘要】现代多媒体信息技术具有形象性、艺术性、趣味性的特点，如果教师在教学中利用现代多媒体信息技术辅助数学教学往往可以使高度抽象的内容具体化、静止内容活动化、数形结合的内容形象化、模拟实验的内容直观化，从而吸引学生的注意力和激发学生的学习兴趣。

【关键词】理解  运用  掌握  深化

【中图分类号】G712   【文献标识码】A 【文章编号】2095-3089（2020）21-0113-02

数学内容自身的特点：抽象、多变、枯燥等，如果教师在课堂上仍然是“一张嘴、一支笔、一块黑板、一本书”的教学模式，会使本来基础薄弱的中职生对数学产生畏惧心理，有可能发展到放弃数学。如何能激起学生对抽象枯燥的概念和严格生硬的定理、公式、法则感兴趣？现代多媒体信息技术具有形象性、艺术性、趣味性的特点，如果教师在教学中利用现代多媒体信息技术辅助数学教学往往可以使高度抽象的内容具体化、静止内容活动化、数形结合的内容形象化、模拟实验的内容直观化，将一些概念和定理变得生动、通俗、具体、直观，就能吸引学生的注意力和激发学生的学习兴趣。如何充分利用多媒体信息技术辅助中职数学教学，是当前中职数学教师要深入进行研究解决的重要课题。下面结合教学实践，谈谈我的一些体会。

一、利用多媒体信息技术使抽象的内容具体化，有助于理解

中专数学教材中许多概念都是由具体的事物观察而抽象出来的。要正确理解概念，就必须引导学生对概念逐字逐句加以推敲分析，对于那些不易被理解的词语，用具体的事例引出并加以归纳，以求把抽象的东西变得更具体化，这样能使学生容易理解数学概念。而多媒体信息技术恰好能巧妙地将具体的事例通过丰富色彩的图片、动听的声音、有趣的动画等融于一体直观地展示出来，让学生经历概念的形成过程并加以归纳，使概念变得简单形象、趣味化。

例如，在讲函数的概念时，如果按照课本用很抽象的语言描述函数的概念，学生理解起来有困难。若运用多媒体信息技术制作实际事例的动画片，突出函数的概念形成过程，给学生具体的印象，有助于理解。展示如下：

1.实例引入：（选用学生熟知的购物情景录制成视频，使学生自然的走向知识点）

动画片里有一位学生说：今天太热了，听说学校商店新进了一批果汁饮料，我得去尝一尝。然后店员告诉他说：“每瓶2.5元。”

（1）问题（质疑、思考）

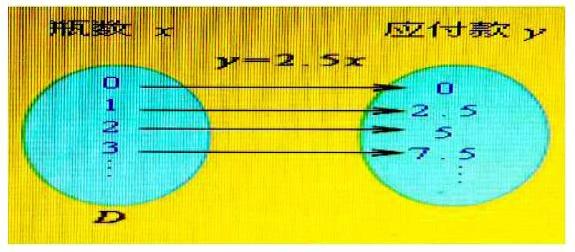
学校商店销售某种果汁饮料，售价每瓶2.5元，购买果汁饮料的瓶数与应付款之间具有什么关系呢？

（2）解决（仔细分析讲解关键词语，引导启发学生体会对应）

设购买果汁饮料x瓶，应付款为y元，则计算购买果汁饮料应付款的算式为y=2.5x。

（3）归纳（充分讲解函数变量和法则之间的关系）

因为x表示购买果汁饮料瓶数，所以x可以取集合{0，1，2，3…}中的任意一个值，按照算式法则y=2.5x，则应付款y有唯一的值与之对应。

两个变量之间的这种对应关系叫作函数关系。

（4）概念（带领学生总结上述问题得到函数概念）

在某一个变化过程中有两个变量x和y，设变量x的取值范围为数集D，如果对于D内的每一个x值，按照某个对应法则f，y都有唯一确定的值與它对应，那么，把x叫作自变量，把y叫作x的函数。

通过多媒体信息技术录制的视频从实例入手展示，把抽象的知识直观地显示出来，同时也刺激了学生的感觉器官，使学生注意力集中到概念的关键特征上，提高理解概念的效果。

二、利用多媒体信息技术使静止内容活动化，有助于运用

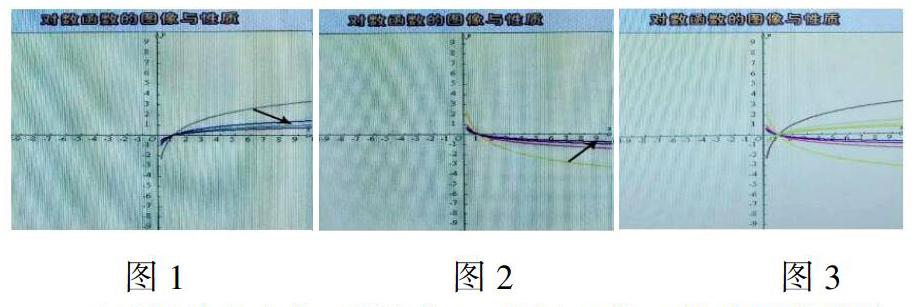
在传统数学教学中，画函数的图像都是用三角板、直尺等手绘“描点法”制作，是静态图形，不能分清同类曲线在同一坐标系中位置关系这一教学难点，要认识它的位置关系需要教师用语言描述和学生的想象能力。而多媒体信息技术画出的图像进行动态展示，能使学生从形式上和图像上直观地对各种现象进行观察、探索，不仅能看清同类曲线在同一坐标系中位置关系，而且可以分清不同类型曲线的变化规律。静态的数学知识动态化，完成了从静止图形到运动图形的飞跃，加强学生的直观印象，加深了感性认识，很快从本质上抓住图像的特征，使学生印象深刻，难以忘怀。

再引导学生仔细观察图3，分析对数函数的图像的特点，能轻易归纳出对数函数y=logax（a>0且a≠1）性质。

利用多媒体信息技术得到对数函数的动态曲线，曲线的变化状况清晰地展示在学生面前，通过教师在教学过程中的点拨，启发学生主动观察、主动思考、归纳揭示问题的本质，总结出对数函数的性质，有助于对知识的发现、接受和运用。

三、利用多媒体信息技术使数形结合的内容形象化，有助于掌握

中职数学研究的对象可分为两大部分：一部分是数，一部分是形，它们称之为数形结合。数形结合是数与几何图形的关系，即通过数与几何图形相互转化来解决数学问题的一种数学思想方法。如我国著名数学家华罗庚说：“数缺形时少直观，形少数时难入微，数形结合百般好，隔裂分家万事非。”在解决数学问题时，借助数量关系的问题转化为与之相应的几何图形性质问题来解决，或者借助几何图形的性质问题来解决数量关系问题。充分利用这种结合，使问题化难为易、化繁为简，从而解决问题。多媒体信息技术的动态变化可以将数与形结合起来，抽象思维和形象思维结合起来，有助于对知识的掌握。

例如，在讲授直线与圆位置关系时，传统的教学是将直线的方程与圆的方程联立组成方程组，通过对方程组的解进行讨论，来研究直线和圆的位置关系，理论上讲是很简单，实际操作的运算过程很麻烦。而利用几何画板演示动画，采用数形结合的方式，通过比较半径与圆心到直线的距离的大小来研究直线和圆的位置关系的方法，把复杂的问题简单化。让学生观察几何画板演示操作过程，固定圆不变，移动直线靠近或远离圆，使直线与圆位置关系发生变化，通过观察、演示，提出问题：

（1）你知道直线和圆有几种位置关系？

（2）移动过程中哪些量在变化？

（3）设圆O的半径为r，直线l到圆心的距离为d， d与r具有怎样的大小关系？

学生通过观察（或动手操作）容易得到结论：

（1）图4：d

（2）图5：d=r：直线与圆相切。

（3）图6：d>r：直线与圆相离。

借助形和数的对应关系，带领学生观察分析，把形的问题转化为数来研究;再通过方程，把数的研究转化为形来讨论。经过这样数形结合的动态展示，引导学生形象地掌握数的变化过程，从中获得感悟，同时也掌握知识。

四、利用多媒体信息技术使模拟实验的内容直观化，有助于深化

对于数据较多、较繁的概率与统计的计算，或者难以演示的数据处理功能实验可利用多媒体信息技术进行模拟操作，把实验引进数学课堂，努力创设符合学生认识规律、适应学生认知结构的“演示情境”，展现给学生，让学生能从屏幕上看到活生生的动态图是怎样操作形成的，这对帮助学生从复杂的内容中理解和区分有着直观的启示作用。

例如，在讲授用样本估计总体时，用频率分布计算实验进行例题的教学，随机抽样30个数据，让学生参与输入30个数据，按确定后数据列表显示30个数据，接着引领学生观察分析数据，其最大值是358，最小值是341，它们的差是358-341=17。取组距为3，确定分点，将数据分为6组。告诉学生分析数据的一种基本方法是用图将它们画出来，一是从数据中提取信息;二是利用图形传递信息。接著在频率分布计算实验输入组距3，按下确定（如下图），最后让学生自己对频率分布表与频率分布直方图进行比较，从而清晰地知道其各自的特点，前者准确，后者直观，两者放在一起，使我们对一组数据的频率分布情况了解得更清晰，更清楚的看到整个样本数据的频率分布情况，估计总体中某事件发生的概率。

通过例题模拟计算实验教学，让学生在参与实践中自己去分析归纳总结出方法，这样使学生体会到用样本估计总体的思想，对相应知识的形成过程也有深刻的理解，使知识掌握得更牢固。

多媒体信息技术进入数学课堂教学，提供了动态演示曲线的形成过程，以生动、有吸引力的事例和动画片、形象逼真的模拟实验来辅助教学，学生有了更多的观察、探索、试验的机会，让学生动手、动脑参与到教学过程中，使他们在参与中发现规律、掌握知识、发展能力，从被动接受变为主动探求，从而突破传统数学教学中的难点，提高课堂教学效率。

参考文献：

[1]刘晓莉，钟敬堂，罗祥华.《多媒体组合教学与数学教学改革》，《数学通讯》，1997.4

[2]蒋春雷.《现代教学媒体在数学教学中的应用》，《数学通讯》，1998.7

[3]晨旭.《数形结合》，《数学通讯》，1996.12