基于增量动态模型的机械数控机床位置控制方法

张 婷，薛媛丽

(陕西机电职业技术学院机电工程系，陕西 宝鸡 721001)

机械数控机床是重要的工业基础装备，直接关系到我国工业领域的发展[1]。机械数控机床是目前应用最广泛的机床之一，主要用于轴类和盘类零件以及任意锥角的内外圆锥面切削与加工，并可进行钻孔和扩孔等操作，因此需采用先进的控制方法对其位置进行控制，从而提高控制精准度。当前，机床控制方法主要分为柔性和刚性两种，利用有限元软件对机床加工耦合性进行控制，可获得较好的控制效果。采用基于视觉引导的传统自动控制方法，结合光电参数进行数控齿轮控制，能够准确修正齿轮转动惯量[2]。该方法虽然提高了机床位置控制精准度，但在加工过程中易受到机床自身振动因素影响，会对精准度产生负面作用。而采用莫尔条纹光电信号补偿控制方法进行位置控制[3]，需根据图纸进行切削加工，工件材料去除率较大，能源消耗较多，控制稳定性较差。

针对上述问题，本文提出了基于增量动态模型的机械数控机床位置控制方法。

1 机械数控机床位置控制结构

数控机床会按照事先编制好的程序，依据工艺路线和相关辅助参数，对零部件进行精准的切割加工等，减少人为造成的加工误差[4]。

交流伺服位置控制系统被广泛应用于高性能机械数控机床中，其采用半闭环控制结构，不以工作台直线位移为位置反馈，结构简单。机械数控机床结构为双环结构，由机械手臂、数控机床、点阵式料仓等组成，如图1所示。

图1 机械数控机床

机械数控机床结构位置精度控制主要是通过光电编码器转动产生的脉冲数来实现，该编码器有增量式和绝对式两种，其中增量式编码器结构相对简单，分辨率较高；而绝对式编码器按照二进制编码输出数据，分辨率较低，但即使电动轴不动也能输出绝对角度信息。光电编码器的引入，使位置控制板能够方便地得到数字化信息，同时也为位置控制提供了有利条件[5]。

在数控机床加工过程中，刀具与工件受到摩擦力的作用，会产生热量，并全部传递给机床[6]，导致零件变形，机床位置发生变化，最终使工件相对位置发生变化。由于机床结构复杂，因此需采用增量动态模型，通过温度和热位移测定、计算机床热变形以及机械数控机床各个部件受热量变化影响的形变量，得到机床温度与加工误差之间的关系，并研究不同形式下热误差动态模型系数[7]。

2 机床热伸长模态

数控机床结构复杂，包含零部件较多，伴随着零部件的摩擦产生的热量会出现传导。图2为机床结构示意图。

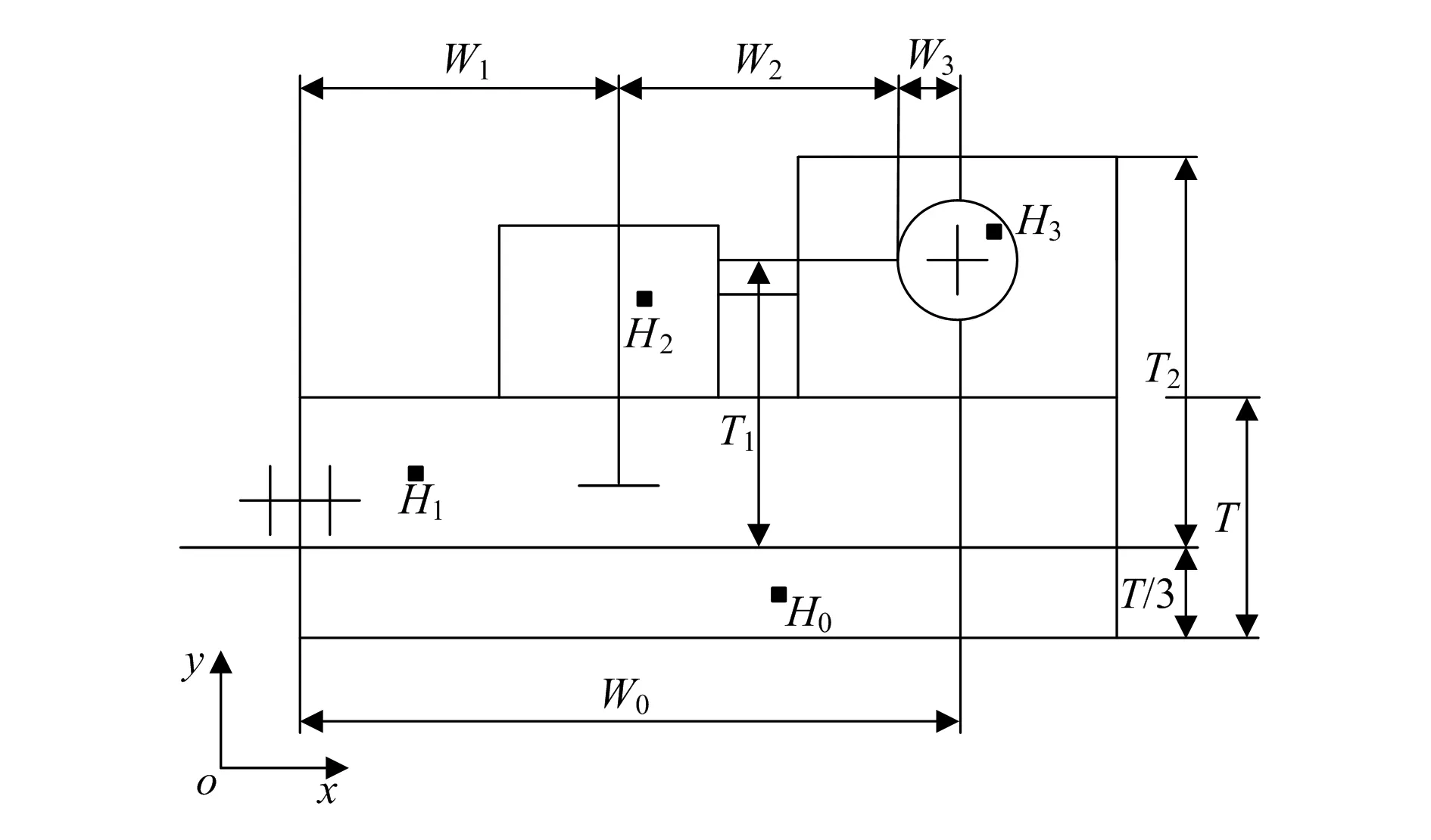
图2 机床结构示意图

机床由床身、丝杠、溜板、主轴箱组成。图中的4个方块分别表示H0，H1，H2，H3温度测点，W0为机床的长度，W1为机床前沿与溜板间的距离，W2为溜板与主轴箱的距离，W3为主轴箱与机床后身的距离，T为机械数控高度，T0为刀具到丝杠的距离，T1为主轴与机床高度中心距离[8]，T2为主轴与机床顶部的距离。

设床身、丝杠、刀具及加工零件热膨胀系数为α，结合图1，计算机床运转位置方向横轴的定位误差k1：

k1=ΔW1=αW1C1

(1)

式中：△W1为机床前沿与溜板间的长度距离误差；C1为H1温度测点测得的温度。整个机床组件与刀具相对位移所产生的热误差动态模型为：

k2=αW0C0-αW1C1-αW2C2-αW3C3

(2)

式中：k2为整个机床组件与刀具相对位移所产生的热误差；C0，C2，C3分别为H0，H2，H3温度测点的温度。

由于W0=W1+W2+W3，则整理式(2)有：

k2=-αW2(C2-C0)-αW1(C1-C0)-αW3(C3-C0)

(3)

依据热误差动态模型[9-10]，用C2代替C0，作为机床运转过程中的参考温度，则式(3)可改写为：

k2=-αW1(C1-C2)-αW3(C3-C2)+α(W1+W2+W3)(C0-C2)

(4)

对于式(3)，如果设定足够多的温度测点，通过获取各点温度值，全面掌控机床各个部件的温度，就可以计算出热量对机床热弯模式下加工精度影响的大小，即整个数控机床的热误差。图3是机床的热弯曲模态示意图。

图3 机床热弯曲模态示意图

图中，H01和H02分别为机床下半部分和上半部分的温度，φ为螺母与机床主轴中心弯曲角度，β为螺母与机床左端弯曲角度。

φ=α(H02-H01)(W2+W3)/T

(5)

β=α(H02-H01)W1/T

(6)

机床热弯曲模态下的热误差动态模型为：

k2=φT2+β(T2-T1)=α(H02-H01)·[(W2+W3)T2+W1(T2-T1)]/T

(7)

由此获得机床运转位置方向横轴的定位误差k1[11]：

k1=α(H02-H01)T1x/T

(8)

式中：x为机床主轴中心的定位。

假设刀具与主轴距离较远时，热误差为正，否则为负，由此分析机床在不同温度下床身底部温度。依据温度系数的正负将已知参数代入式(3)中，以补偿热误差。

3 构建机械数控机床目标控制函数

在外部干扰条件下，分析主轴加工工艺参数的约束分量，考虑自身振动干扰条件，设计控制平动速率函数[11-12]。依据稳定性控制原理，修正、调整数控机床加工过程中的稳定收敛程度。

在高强度运行环境下，构建增量动态模型，获取机床主轴振动响应函数，设λi为相对运动轨迹，Li为组件坐标系原点的旋转轨迹，由此构建增量动态控制模型：

(9)

式中：μ为最终定位误差。在数控机床往复平移过程中，结合各组件的旋转轨迹，确定切削参数以计算切削速度，并根据λi最终值得到主轴振动响应的收敛值。由于切削时间与参数设置密切相关，因此通过优化轴向进给量，可得到数控机床控制的稳态误差。

4 误差校正

在组件位置控制过程中，因为温度变形是影响控制精确度的主要因素，所以机床坐标位置控制精度主要取决于温度测试点获取信息的准确程度。本文采用信息补偿法提高机床位置检测精度，具体步骤如下：

1)分析装置误差与结构状态关系，建立误差关系增量动态模型。在数控机床整个工作过程中，数控系统依据检测装置获取温度信息，按照增量动态模型计算误差补偿值，依据此检测装置测量值实时校正，保证机床在运转过程中能沿着坐标轴运动。

2)在高精度坐标基础上，获取多坐标合成轨迹，采用几何误差信息校正方法，对固定圆弧轮廓进行测量。当机械数控机床坐标间存在不垂直误差时，测量的轨迹将不精准，通过对比分析实际轨迹与标准轨迹，求出坐标间不垂直误差，并校正运动位置，从而精准控制机械数控机床位置。

5 实验测试分析

为了验证基于增量动态模型的机械数控机床位置控制方法的有效性，以某生产厂家一种车削加工中心的数控机床为研究对象，进行实验测试分析。

5.1 实验环境与参数设定

实验采用高速干切滚机械数控机床，配置西门子840D系统。用4台数控机床通过干切滚刀对齿轮进行加工操作，对得到的数据进行分析。

加工工件材料为20CrMnTi，滚刀数量为4个，干切滚刀厚度为3.0 mm，加工工件齿轮数为40，其精度相对误差在0.15%以内，切深为0.5 mm，机床主轴转速为8.0 mm/rad。具体实验环境如图4所示。

由图5解算结果可知，当加工工艺参数达到一定值时，加工工艺的收敛性能表现良好。随着时间的增加，机床轴向进给速度和齿轮角度曲线趋近于稳定状态，能够有效保证机床位置控制误差快速收敛无限趋近于零，由图5可知，齿轮方向角度为-7°，进给速度为80 m/s时，能够达到实验要求。

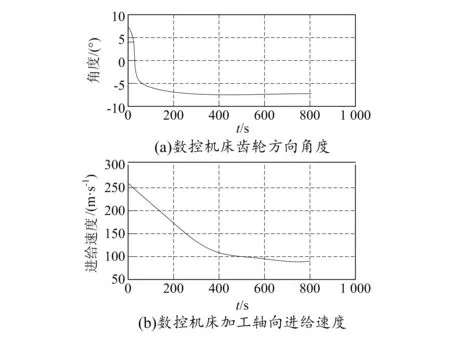
图5 加工工艺参数优化解算

5.2 时间常数确定

通过对比实测阶跃响应和MATLAB模型实验结果，确定实验的时间常数。

记录位置控制方法输入的阶跃信号时，将编码器反馈的前50个点在MATLAB中用PLOT命令绘制成图形，如图6所示。

由图6可知，当时间在0～0.05 ms范围内时，实验对象位移变化波动较大，其范围为[0，125]。而时间在0.05～0.40 ms范围内时，位移基本保持不变，始终为100。

依据图6所示实际阶跃信号响应实验结果，分别令操作的单位时间为3，5，10 ms进行阶跃响应实验，结果如图7所示。

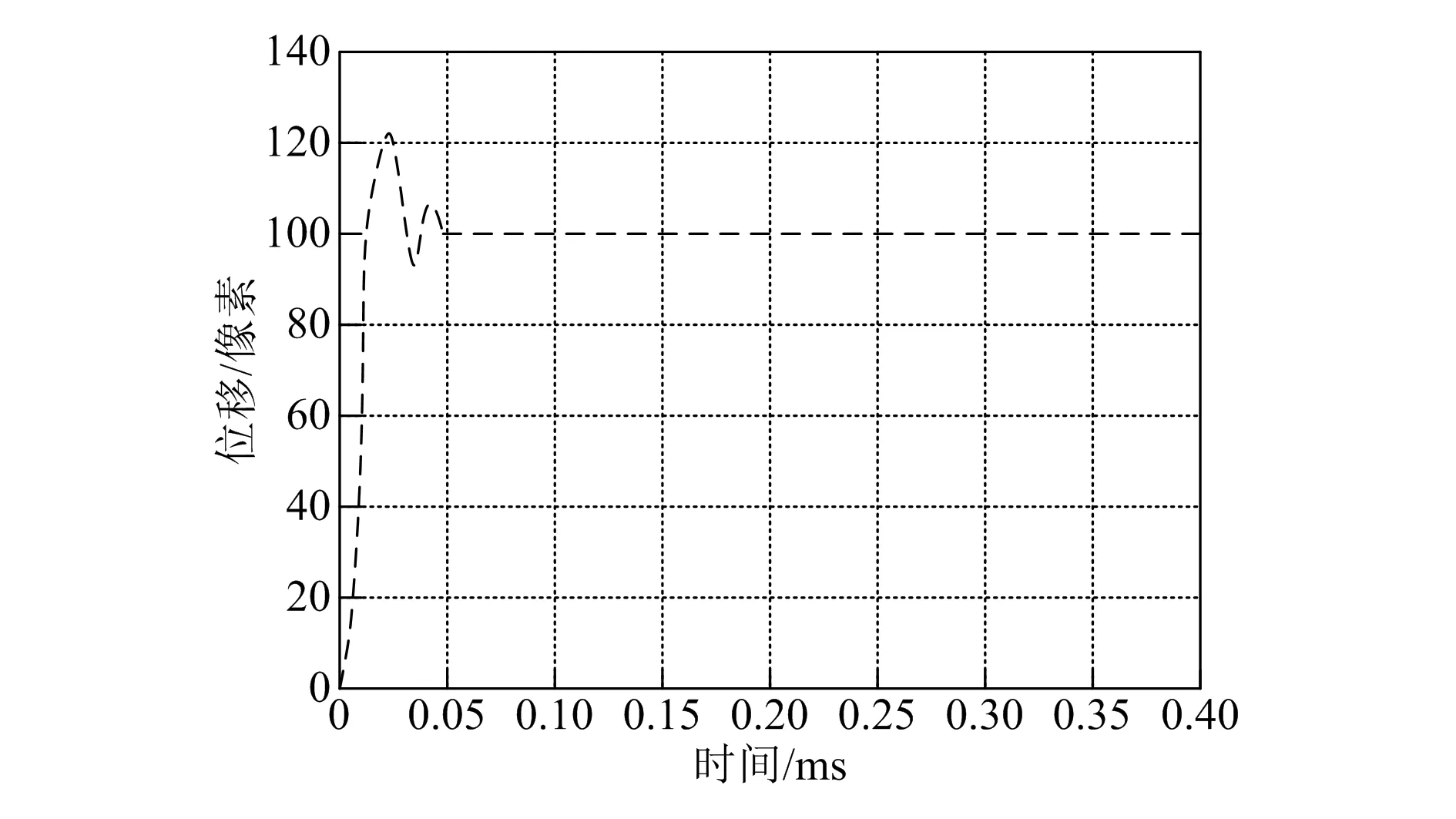
图6 实际阶跃信号响应实验

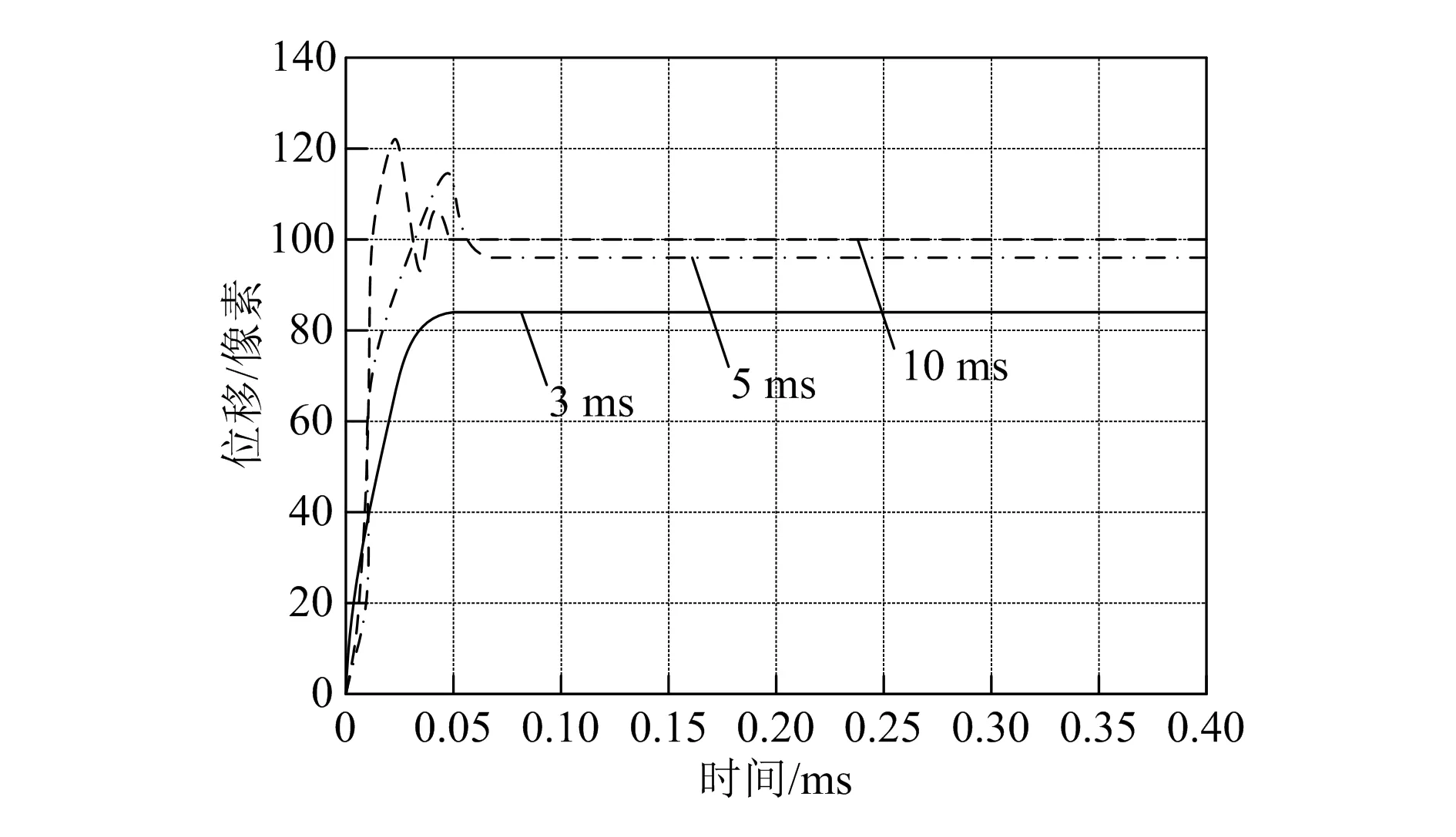
图7 3，5，10 ms下阶跃响应实验结果

通过图7可知，当操作的单位时间为3 ms时，位移变化范围为[0,85]；当操作的单位时间为5 ms时，位移变化范围为[0,115]；当操作的单位时间为10 ms时，位移变化范围为[0,120]，与实际阶跃信号响应实验结果一致，由此可确定时间常数为10 ms。

根据图8可知，采用增量动态模型控制方法，随着迭代时间的增加，误差接近于0 ms；采用视觉引导控制方法,随着迭代时间增加误差逐渐减小，误差最高为0.45 ms，最低为0.15 ms；采用莫尔条纹控制方法，随着迭代时间的增加误差减小，误差最高为0.42 ms，最低为0.21 ms。

图8 不同方法数控机床位置控制误差对比图

根据数据平均值稳健性，对不同控制方法的误差平均值进行计算，结果见表1。

表1 不同控制方法的误差平均值对比

由表1可知，采用增量动态模型控制方法平均误差明显小于视觉引导和莫尔条纹控制方法，可见增量动态模型控制方法稳健性高，说明该方法在一定运行时间下机械数控机床位置控制具有较高的精准度。

分析采用增量动态模型控制方法在不同位置的几何误差，结果见表2。

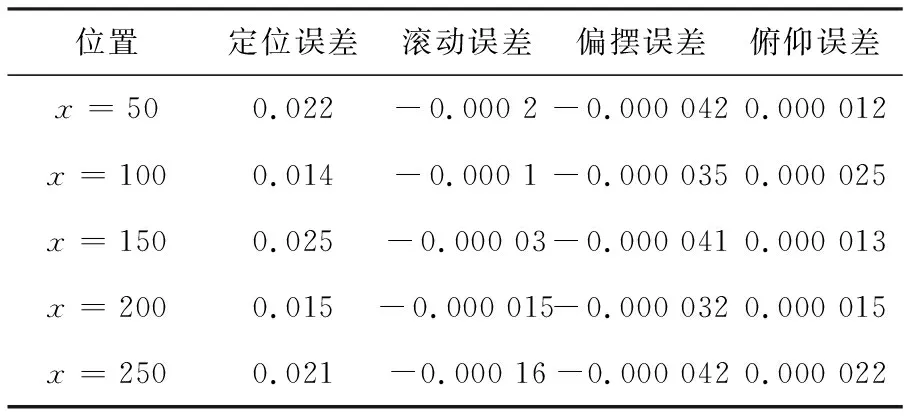
表2 增量动态模型控制方法在不同位置下的几何误差 mm

由表2可知，在不同位置下，本文方法仅存在极小误差，这可能是控制过程中由于机械自重影响产生的。

6 结束语

针对机械数控机床的需求，本文研究一种基于增量动态模型的机械数控机床位置控制方法。机床热变形过程可视为不同形状的热变形模态叠加过程，通过分析机床热变形模态，计算不同测试点温度下机床热变形程度，将模态中组件变形全部叠加起来作为总变形，为机械数控机床位置控制提供精准数据。本文所述控制方法通用性强，为机械数控机床位置精准控制提供了一种新的解决方案，为位置控制提供了一定技术支持。但是，目前仅仅是通过理论研究来验证实现方案的有效性，为了在实践中体现出真正价值，还需进一步完善复杂数据模型。