状态微分反馈控制与压水反应堆功率现有两种控制系统的等价性研究
2020-07-14栾秀春王俊玲杨志达
栾秀春,刘 磊,王俊玲,杨志达,周 杰,*
(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001;2.中国原子能科学研究院 反应堆工程技术研究部,北京 102413)
1955年,Schultz编撰了第1部关于反应堆控制的教科书[1]。在当时,研究方法包括尼科尔斯表、奈奎斯特分析、根轨迹、伯德图等,这些均依赖于输入输出形式的系统描述,特别是传递函数[2]。从20世纪中叶以来,现代控制理论获得了很大的发展,并用于反应堆控制系统的设计,尤其是线性二次调节器(LQR)的应用[2-3]。1970年,Mohler和Shen[4]完成了一部内容为应用最优控制理论设计反应堆控制系统的教科书。
Edwards等[5-6]将状态反馈辅助经典控制(SFAC)用于控制反应堆的一回路冷却剂温度,获得了较常规控制器改善的性能和稳定的鲁棒性。以此为基础,文献[7]提出了用带回路成型的线性二次调节器(LQG/LTR)设计的鲁棒SFAC,文献[8]提出了基于改进的SFAC结构的LQG/LTR控制器。Cho和Grossman[9]将面向负荷跟随条件下氙空间震荡的最优控制器的设计,转化为线性二次型跟踪问题。为抑制反应堆中氙的空间震荡,Park和Cho[10]建立的镇定控制方案采用了极点配置和线性观测器理论。
由于神经网络能描述非线性映射,基于准对角神经网络的数字PID控制器[11]和利用多层感知器神经网络的智能控制器[12]能提高反应堆的负荷跟随能力。模糊规则能有效地表达工业领域中运行专家的现场经验,因此基于模糊规则的控制器能提高反应堆控制系统的性能[13-14]。在制定模糊规则的过程中,存在主观随意性,引入遗传算法来优化模糊规则可改善性能[15-16]。
模型预测控制是一种源自工业过程系统控制的方法,也已用于反应堆功率的控制。文献[17]针对负荷跟随运行条件下的功率控制和轴向功率分布,将模型预测控制器与参数估计器相结合,来应对工作点的改变和时变特性。文献[18]采用数据驱动方案,设计负荷跟随运行模式下的堆芯功率的子空间预测控制系统。
现有的大部分压水堆的控制棒的控制机制有两种实现形式,即基于控制棒位置的控制和基于控制棒速度的控制[2]。本文目的是提出一种方法,来描述反应堆的这两种控制系统的等价性。
1 基于控制棒位置的功率控制器
在反应堆功率的经典控制系统中,输入到反应堆的反应性是通过设定控制棒的位置来实现的。
出于计算方便的目的,通常使用等效单组缓发中子的点堆动力学方程的归一化形式[2]:
(1)
(2)
式中:nr=n/n0,为相对中子密度,n为中子密度(cm-3),n0为额定功率(稳态)的中子密度(cm-3);ρ=(k-1)/k,ρ为反应性,k为增殖因数;β为总缓发中子份额;Λ为瞬发中子代时间,s;λ为等效单组缓发中子先驱核衰变常量,s-1;cr=c/c0,为缓发中子先驱核的相对密度,c为缓发中子先驱核浓度(cm-3),c0为额定功率(稳态)的缓发中子先驱核的密度(cm-3)。
式(1)、(2)在平衡工作点的线性化形式[2]为:
(3)
式中,nr0为在平衡工作点的相对中子密度。
式(3)改写成状态空间方程的形式为:
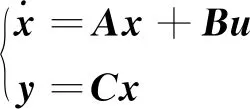
(4)

对于式(4),为让输出Δnr(t)跟踪参考输入信号r(t),可设计积分形式的反馈控制律为:
(5)
反馈控制律(5)是增广被控对象

(6)
y(t)=Cx(t)
(7)
的状态反馈控制,可通过多种成熟的方法设计,如极点配置、LQR、H∞等[19-21]。设计所得的控制系统结构如图1所示。

图1 积分控制系统结构
2 基于控制棒速度的功率控制器
在工程实践中,使用误差信号设置控制棒位置,实现起来很困难。在实际的反应堆功率控制应用中,现实可行的控制机制是使用控制棒速度作为输入信号。图2示出了以控制棒速度作为输入信号的系统方框图[2]。

图2 使用控制棒速度的反应堆控制的系统方框图
根据图2,在式(1)、(2)的基础上增加1个微分方程[2],有:
(8)
式中,Gr为控制棒总的反应性价值,Δk/k。
式(1)、(2)、(8)在平衡工作点的线性化形式[2]为:
(9)
式(9)改写成状态空间方程的形式为:

(10)

对于式(10),控制器也可采用积分控制(5)的形式,但闭环系统的阶次将会较图1的高。对照图1、2可看出,在两图中的前向通道上均有1个积分环节。所以,可利用式(8)中的积分器来设计反馈控制律,从而使所得的闭环系统具有与图1相同的阶次。
3 状态微分反馈
设被控对象定义为:
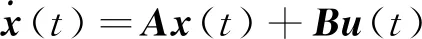
y(t)=Cx(t)
(11)
此被控对象的执行器可看作是1个积分器,有:
yact(t)=Cactxact(t)
(12)
执行器与被控对象联结,满足:
u(t)=yact(t)
(13)
由执行器与被控对象构成的广义被控对象表示为:
y(t)=Cx(t)
(14)
(15)
对于广义被控对象(15),设计反馈控制律:
uact=-KDw+kP(r-y)
(16)
式中,w为反馈信号,由下式构造:
w(t)=Ax(t)+Bu(t)
(17)
对照式(17)与式(11),可得:
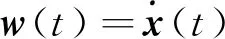
(18)
信号w代表被控对象(11)的状态的微分,因此,称反馈控制律(16)为状态微分反馈控制。根据式(12)、(13)、(17),可得:
uact=-KD[Ax(t)+Bu(t)]+kP[r-Cx(t)]=
(19)
以上给出了状态微分反馈控制的定义,而这一控制律的设计则依赖于等价性定理。
4 等价性定理
根据被控对象(6)设计的控制器(5),与根据被控对象(15)设计的控制器(16),两者参数间的关系可表达如下定理。
定理:当被控对象(6)和控制器(5)构成的闭环系统与由被控对象(15)和控制器(16)构成的闭环系统具有相同的动态特性时,式(20)、(21)成立。
(20)
(21)
证明:由被控对象(6)和控制器(5),得闭环系统:

(22)
(23)
传递函数矩阵为:
(24)
为计算式(24)中的逆矩阵,令:
(25)
则式(24)变换为:
(26)
计算分块矩阵(25)的逆矩阵[22],得块矩阵:
M22=[sI2-(-C)(sI1-A+BK)-1(BKI)]-1
(27)
(28)
因此,闭环系统(22)、(23)的传递函数矩阵具有如下形式:
(29)
由被控对象(15)和控制器(16)、(17),可得闭环系统:
(30)
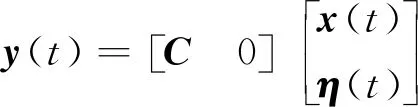
(31)
其传递函数矩阵为:
(32)
为计算式(32)中的逆矩阵,令:
(33)
则式(32)变换为:
(34)
计算分块矩阵(33)的逆矩阵[22],得块矩阵:
N22={sI2+BactKDBCact-
[Bact(KDA+kPC)](sI1-A)-1(-BCact)}-1
(35)
N12={s2(BCact)-1+s[BactKD-(BCact)-1A]+
BactkPC}-1
(36)
因此,闭环系统(30)、(31)的传递函数矩阵具有如下形式:
(37)
当被控对象(6)和控制器(5)构成的闭环系统与由被控对象(15)和控制器(16)构成的闭环系统具有相同的动态特性时,两者的传递函数应相等,即:
GI(s)=GSDF(s)
(38)
根据式(29)、(37)、(38),可得:
(39)
由式(39),可得:
(40)
(41)
经过进一步的简化,得:
证明完毕。
5 控制系统设计及仿真
表1列出了典型的压水型反应堆在额定功率工况下的参数[2],用于控制系统设计、分析和仿真。

表1 反应堆参数
对于基于控制棒位置的反应堆功率模型(1)、(2),应用极点配置来设计控制器。文献[2]在根轨迹分析的基础上,依据最佳阻尼比,并考虑控制器设计的灵活性,确定主导极点为一对共轭极点,并保留开环系统中远离虚轴的极点,故将极点配置在p1=-0.2-0.2j,p2=-0.2+0.2j,p3=-65。本文也采用这组极点,则可获得反馈控制律(5)为:K=[2.750 0×10-5-0.012 443 5],KI=0.004 16。
使用式(11)~(13)的形式来描述基于控制棒速度的反应堆功率模型(1)、(2)、(8),表示为:
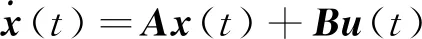
y(t)=Cx(t)
(42)
yact(t)=Cactxact(t)
(43)
u(t)=yact(t)
(44)

应用上述定理的结论设计状态微分反馈控制器,可得KD=[0.002 750 0 -1.244 35]、kP=0.416 0。
为演示所设计的控制器的有效性,在由点堆动力学方程描述的反应堆功率模型上,应用MATLAB 2011a中的Simulink进行数值仿真。本文采用3种不同的过渡过程来评价上述所设计的两种控制器的性能,并进行比较,指令功率的斜坡变化信号如下。
1) 局部控制工况:以额定功率为基准,功率水平按照5%/min的速率斜坡变化100%→95%→100%;
2) 全局运行工况:以额定功率为基准,功率水平按照5%/min的速率斜坡变化100%→5%→100%;
3) 紧急运行工况:以额定功率为基准,功率水平按照15%/min的速率斜坡变化100%→20%。
图3为局部控制工况的系统运行曲线。可看出,状态微分反馈控制系统能快速达到期望功率水平,超调很小且无震荡;控制棒速度的状态微分反馈控制系统与控制棒位置的积分控制系统的响应曲线几乎重合,差别很小。
图4为全局运行工况的系统运行曲线。可看出,期望的过渡过程被快速实现,控制棒速度的状态微分反馈控制系统几乎无功率超调和震荡,反应性过渡平稳;控制棒位置的积分控制系统有较小的功率超调,并存在反应性响应的震荡。

图3 局部控制工况的系统运行曲线

图4 全局运行工况的系统运行曲线
图5为紧急运行工况的系统运行曲线。控制棒速度的状态微分反馈控制系统中,反应堆的功率输出无超调和震荡,反应性过渡平稳,这说明状态微分反馈控制系统能在紧急运行工况下调节反应堆功率;控制棒位置的积分控制系统具有较小的功率超调和震荡,并存在反应性响应的震荡。
综合图3~5,在系统运行过程中反应性远小于β/2,即两种控制系统均满足反应堆安全运行的要求[23];由于上述两种控制系统均依据在额定工况负荷工作点线性化的数学模型设计,而数值仿真中的被控对象采用非线性模型,故在局部控制工况下,两者的性能差别很小,而在全局运行工况和紧急运行工况下,偏离设计工况点较远,控制棒速度的状态微分反馈控制系统的负荷跟随调节能力优于控制棒位置的积分控制系统。
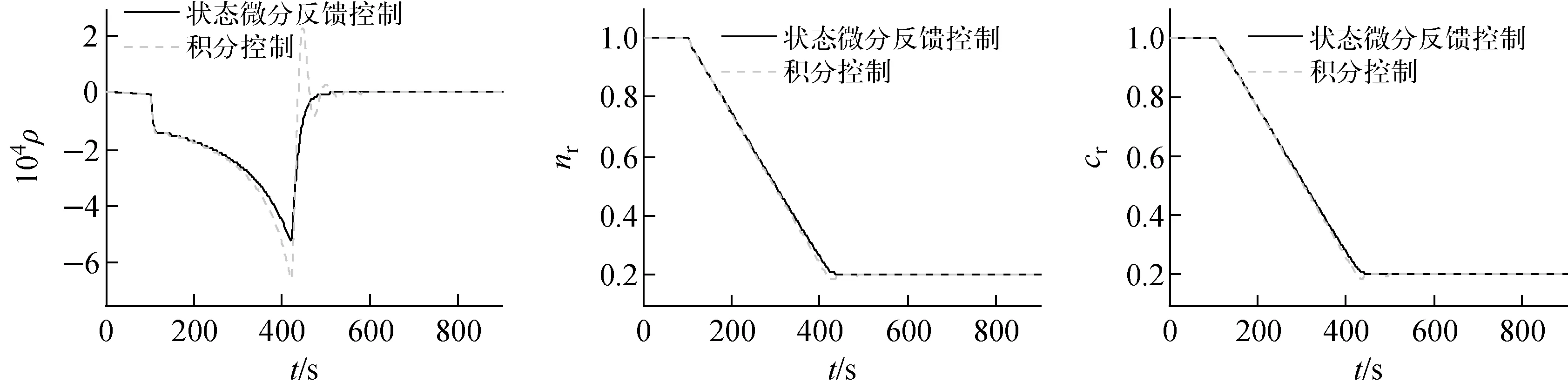
图5 紧急运行工况的系统运行曲线
6 结论
反应堆控制棒的控制机制有两种实现形式,即基于控制棒位置和基于控制棒速度。现有的技术——积分控制和极点配置,用于为前者设计控制器。一种新方法——状态微分反馈控制,为后者设计控制器而提出。本文讨论了这两种控制系统的等价性,并总结为等价性定理。根据此定理,为基于控制棒速度的功率过程设计了状态微分反馈控制器。数值仿真结果表明,依据本文所列典型参数的反应堆功率的状态微分反馈控制系统,具有很好的负荷跟随调节能力。
