考虑端面变形微孔表面无压动压润滑比较分析
2020-07-14丁少鹏史正良刘鹏飞关蕴奇
丁少鹏, 徐 嘉, 史正良, 刘鹏飞, 关蕴奇
(1.空调设备及系统运行节能国家重点实验室, 广东 珠海 519070; 2.珠海格力电器股份有限公司, 广东 珠海 519070)
引言
压缩机是制冷、空调装置中的主要能耗设备,且在运行过程中存在诸多摩擦副配合,摩擦副间摩擦磨损引起的能量损失约占整个压缩机系统的10%~30%,造成输入轴功率增大,制冷系统能效比降低。尤其随着家电产业新型绿色环保制冷剂的引入,迫使压缩机工况复杂化,润滑条件更为恶劣,摩擦副间摩擦磨损问题愈发严重,而表面纹理织构技术可以利用精细加工方法实现表面形貌精确控制以改善润滑状态,延长使用寿命、减少能耗。
微孔织构提供流体膜动压承载能力,且能够存储润滑剂、容纳磨损颗粒,显著提高端面的抗磨损性能,因此获得广泛关注。KLIGERMAN和ETSION较早将圆形微孔引入到密封端面中并建立相关润滑分析模型,随后展开微孔分布形式[1]、孔型参数优化[2-3]、密封动静压实验[4]等研究,指出:当端面开孔面积比为0.65,孔深为5~10倍间隙膜厚时,局部开孔端面具有较高综合密封性能[3],且相比于普通机械密封,微孔端面摩擦转矩可减小40%,温升可降低20 ℃[4]。为提高圆形微孔动压特性,将倾斜微孔引入润滑端面,通过方向性微孔对流体的导向和汇聚作用,产生更强动压效应[5-7],提升端面润滑与摩擦性能。白少先等[8-9]展开椭圆微孔结构参数的优化设计,认为微孔倾斜角在30°~50°范围内动压效应最为显著,相比于圆孔,最优孔型设计可提升端面开启力达到20%,之后在水润滑和油润滑条件下,实验对比光滑表面、圆形和倾斜椭圆微孔表面摩擦规律:微孔表面摩擦系数和润滑温升明显小于光滑表面,且倾斜椭圆微孔表面小于圆孔表面。
目前,国内外学者微孔织构领域研究主要集中于单一孔型结构润滑机理分析与特征参数优化,如圆孔[10-12]、椭圆孔[13-16]、菱形孔[17-18]、三角形孔[19]等,而未展开相同工况条件下的不同孔型润滑性能与摩擦特性的对比分析。
本研究以圆形、椭圆形、矩形、菱形、方形、三角形等6种不同微孔表面结构为研究对象,考虑端面弹性变形影响,开展了无压工况下动压润滑特性的比较研究,数值分析平衡基础膜厚、流体流量、摩擦转矩、摩擦系数等性能参数随不同操作条件与微孔结构参数变化规律,并以最优动压特性与摩擦性能为目标,给定不同孔型参数的优化范围。
1 理论模型
不同微孔润滑端面结构如图1所示,摩擦副采用相对转动的环面-环面配合,动环端面以一定角速度ω做匀速转动,静环端面保持静止状态,在其任一端面从内径到外径以转轴为中心加工密集排布微孔结构,包括圆孔、椭圆孔、菱形孔、矩形孔、正方形孔、三角形孔等6种孔型,并沿径向与周向呈均匀分布。
定义开孔面积比Sp表征端面微孔面积与整个润滑区域面积的比值:
(1)
式中,nθ,nr分别为周向和径向微孔数量;a,b分别为微孔长轴与短轴长度;而对于圆形,a为孔径,对于正方形与三角形,a为边长;ro,ri分别为圆环端面外径与内径长度。
此外,为描述微孔方向性特征,定义微孔特征参数,即:微孔倾斜角β表征微孔倾斜方向,定义为微孔中心线与x轴反方向夹角,圆形微孔表面润滑特性不随倾斜角变化;方向因子γ=a/b,定义为微孔长轴与短轴之比,圆形孔、正方形孔、三角形孔表面润滑特性不随方向因子变化。
液体润滑介质假定为牛顿流体,黏度保持不变,且沿膜厚方向无压力变化,则柱面坐标系Reynolds方程记为:
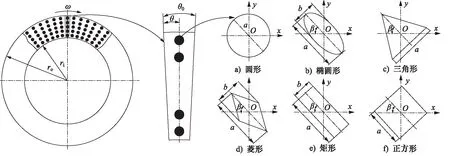
图1 不同微孔润滑端面结构示意图
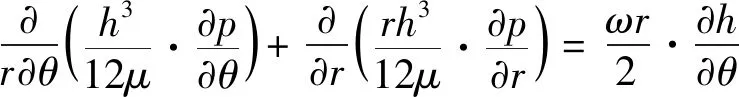
(2)
式中,p为流体膜压力;μ为流体黏度;r,θ分别为径向与周向坐标;h为润滑区域间隙尺寸。
h(r,θ)=h0(r,θ)+hd(r,θ)+hdef(r,θ) (3)
式中,h0为摩擦副润滑间隙基本尺寸;hd为微孔深度,非开孔区hd=0;hdef为润滑端面弹性变形引起的膜厚变化。
强制性与周期性压力边界条件为:
p(r=ri,θ)=p(r=ro,θ)=pa
(4)
p(r,θ=0.5θ0)=p(r,θ=-0.5θ0)
(5)
式中,pa为标准环境大气压力,1.01325×105Pa;θ0为计算区域角度取值范围。
润滑端面性能参数主要包括:流体膜基础厚度h0、流体流量Q、摩擦转矩T和摩擦系数f。
流体膜基础厚度h0根据油膜承载力与外加负载间的力平衡关系求得,外加负载为定值,油膜承载力F定义为:
(6)
流体流量Q计算公式为:
(7)
润滑区域流体处于全膜润滑状态,因此端面间摩擦可视为流体摩擦,则端面间的摩擦力Ff定义为:
(8)
故摩擦转矩T为:
(9)
若外加负载为W,则摩擦系数f为:
(10)
计算过程中,采用有限差分法求解流体控制方程,对二阶偏微分项应用中心差分格式,对一阶偏微分项应用迎风差分格式,另外,采用有限单元法计算润滑端面弹性变形,划分网格时采用空间20节点六面体等单元。应用当量圆环计算端面变形,圆环厚度为10 mm,内外径界面施加内外压力载荷即环境压力,圆环一侧端面承受流体膜压力,另一侧端面设置轴向位移约束,周期性边界采用周期性位移约束。
网格密度对计算结果影响显著,如图2所示,随网格数的增加超过100×100时,端面摩擦扭矩基本保持不变,计算误差控制在0.3%以内,且密度越大耗时越长,综合选取100×100的网格可满足计算要求。
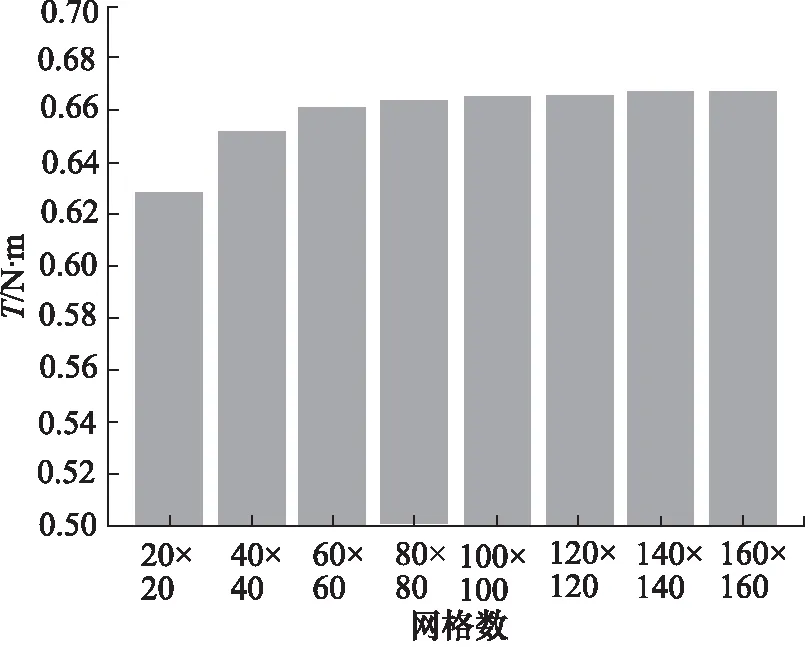
图2 摩擦转矩随网格密度变化
此外,计算过程中,根据力平衡关系采用二分法调整膜厚分布,载荷收敛残差为1×10-3,平衡基础膜厚收敛过程如图3a所示。为验证控制方程求解的准确性,采用文献[20]单个圆孔结构计算结果进行对比分析,如图3b所示,压力差异控制在3%以内。
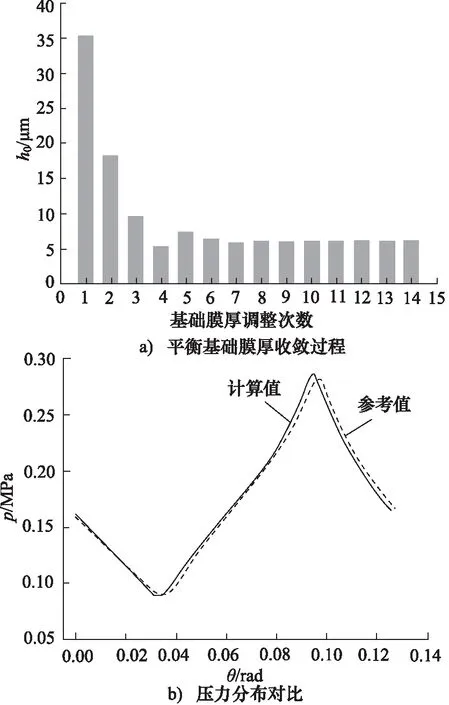
图3 模型验证
2 结果分析与讨论
表1所示为润滑端面的主要结构参数与操作条件。计算过程中,配合摩擦副的动环材料选为GCr15SiMn,静环材料选为HT250,所涉及材料参数见表2。
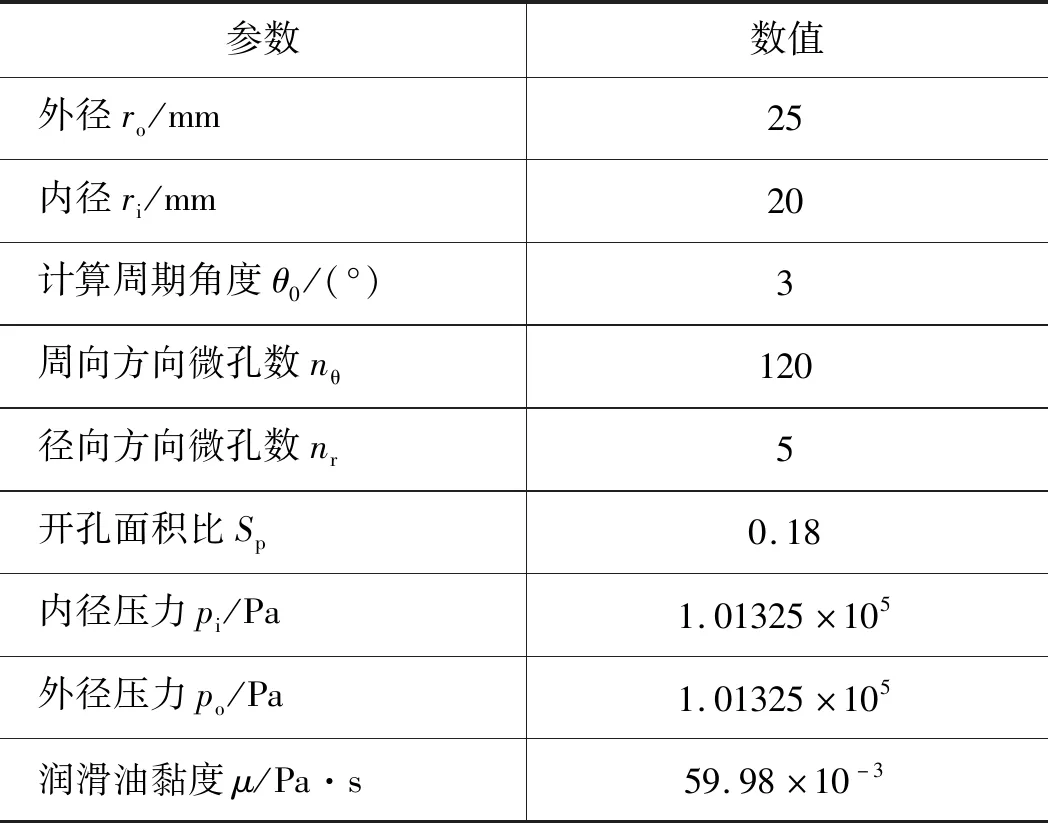
表1 润滑端面结构参数与操作参数

表2 材料相关参数
2.1 压力分布
图4所示为工况转速ω=2000 r·min-1、孔深hd=4 μm、倾斜角β=60°、外界负载W=800 N、方向因子λ=2时,椭圆微孔端面压力分布情况。随动环端面作周向剪切运动,流体介质进入润滑间隙,并沿椭圆微孔长轴方向流动,在微孔收敛间隙侧不断富集,形成动压效应,显著提升压力分布,相应地,在发散间隙侧压力迅速降低,甚至发生空化现象。椭圆微孔方向性倾斜增加对流体的引导作用,进一步增强流体动压特性。
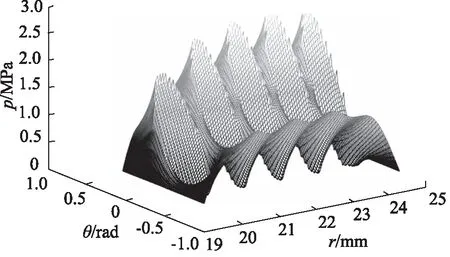
图4 椭圆微孔端面压力分布
图5所示为椭圆微孔润滑间隙膜厚分布以及端面轴向变形情况(不包含孔深)。弹性变形改变润滑端面几何形状,由于端面受到流体膜压力的挤压作用,图中所示变形量均呈现负值,其中最大变形发生在流体膜压力峰值点附近,相应地,空化区域流体膜压力最低,其端面变形量最小。总体来讲,端面最大变形量仅能达到0.07 μm左右,而平衡基础膜厚可达到5.78 μm 左右,变形量约为基础膜厚的1.21%,可见端面变形对膜厚分布影响微弱,全膜润滑分析时可不予考虑。端面变形与流体膜厚度相对应,轴向压缩变形越大,润滑间隙尺寸越大,膜厚越厚。
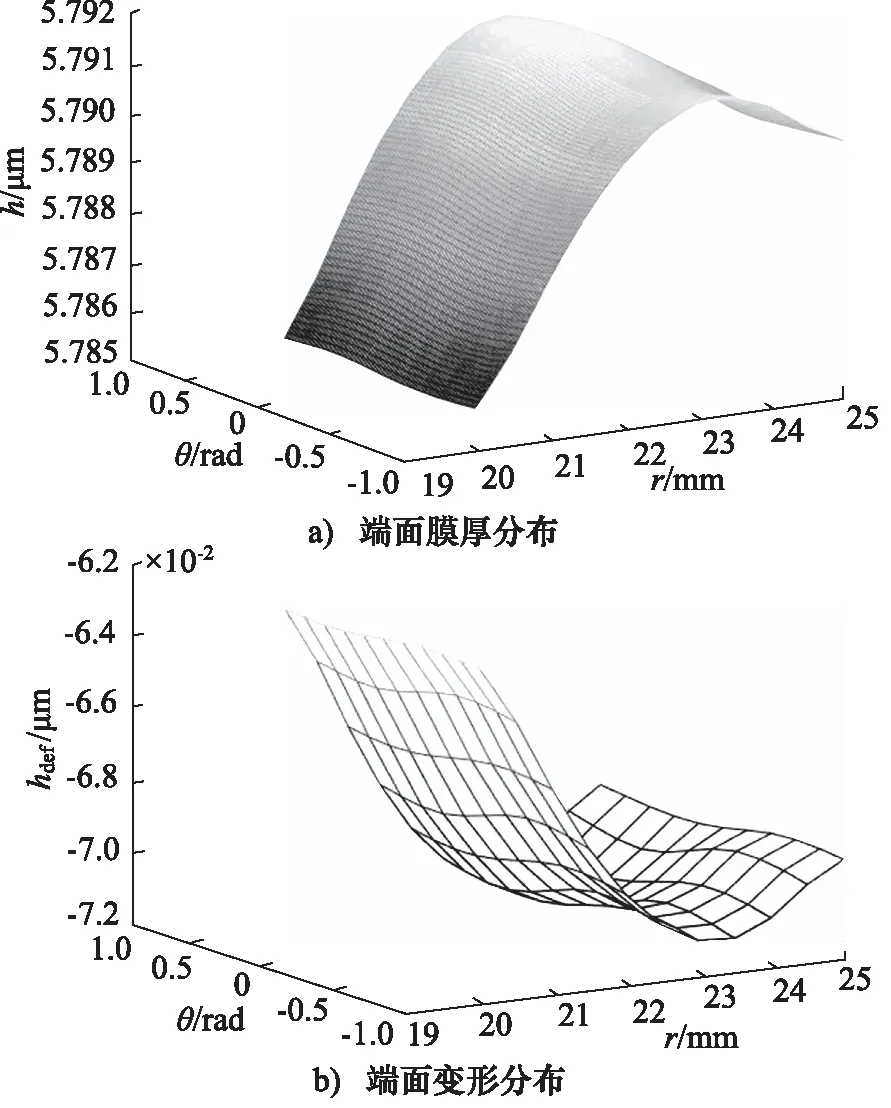
图5 椭圆微孔端面膜厚与变形分布(不包含孔深)
不同微孔端面计算区域中心轴线压力分布比较如图6所示,孔区的存在产生充足动压效应,提升整体膜压分布,随流动方向,在微孔收敛侧压力急剧升高,而在发散侧压力快速降低。6种孔型结构中,3种典型的方向性倾斜微孔,椭圆形、矩形、菱形,动压效应最为显著,压力峰值最高达到1.5 MPa,而另外3种微孔结构,圆形、方形、三角形,动压效应相对减弱,这与方向性微孔导流作用密切相关。
图6 不同微孔端面计算区域中心轴线压力分布比较
2.2 操作参数影响
1) 载荷影响
针对6种孔型端面,进行不同操作工况下的润滑特性分析,图7展示为外加负载对平衡基础膜厚、流体流量、摩擦转矩以及摩擦系数的影响。随负载从100 N到1600 N变化,基础膜厚逐渐减小以提供更大动压效应,平衡闭合力作用,尤其当负载小于400 N时,微孔动压特性变化显著,引起膜厚衰减更为明显。负载增加造成膜厚减小,通过式(8)定义,结果使得流体间摩擦力增加,因此摩擦转矩随负载变化呈现增加趋势。而摩擦系数变化趋势与平衡膜厚相似,由于负载增长幅度大于摩擦力增长幅度,所以负载越大,摩擦系数越小。
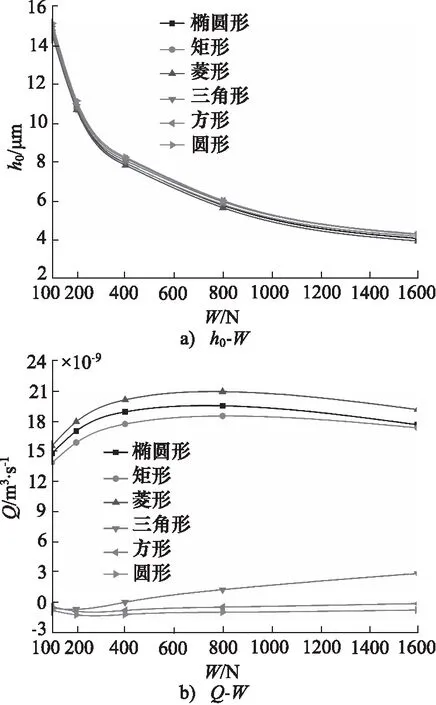
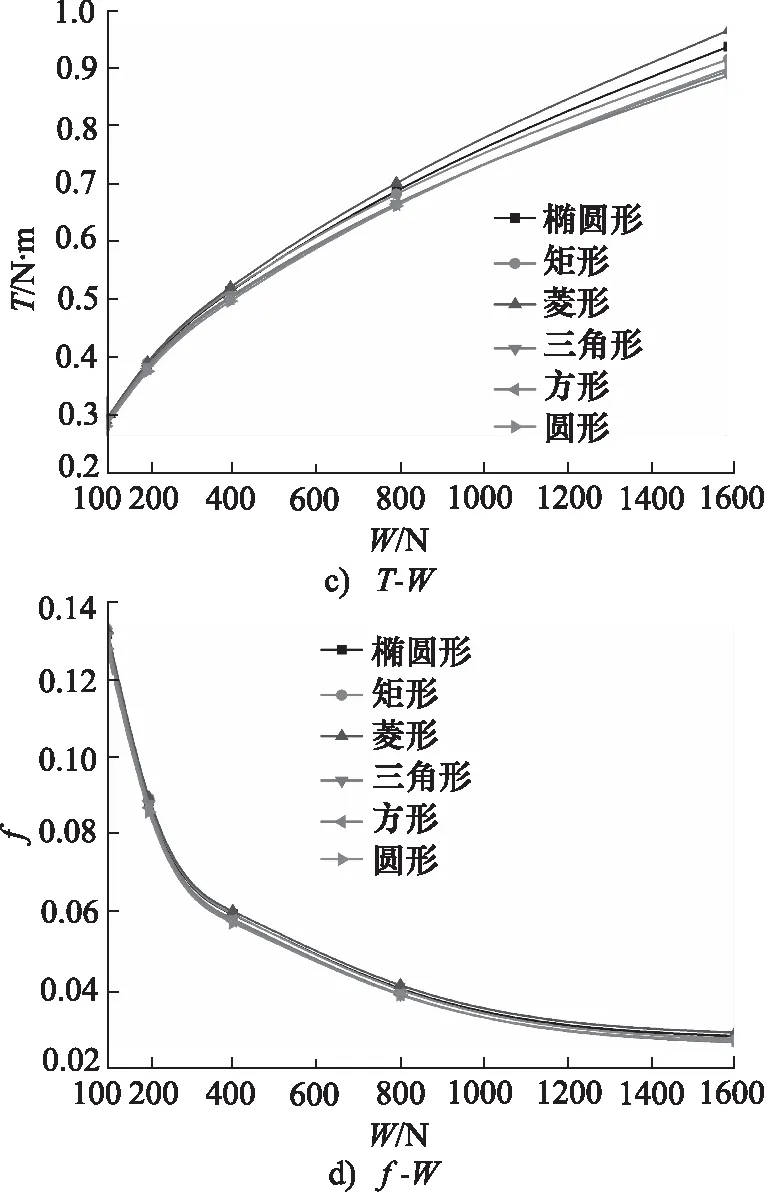
图7 负载对润滑特性影响(hd=4 μm, β=60°,λ=2,ω=2000 r·min-1)
对于方向性倾斜微孔,椭圆形、菱形、矩形,微孔长轴方向性导流作用,在周向剪切作用下诱发流体从外径向内径流动,流体流量呈现正值,且随负载增加,流量呈现先增后减的趋势,当W<400 N时,压力梯度增加的影响大于膜厚衰减的影响,占据主导因素,造成流体流量增长,而随负载继续增加,微孔动压效应增幅减弱,基础平衡膜厚的变化占据主导因素,随膜厚缓慢减小,造成流量呈现微小下降趋势。而对于圆形、方形、三角形孔,由于不存在长轴方向性导流作用,在无边界压差环境下,流体流量数值较小。
对比6种孔型结构,在hd=4 μm,β=60°,λ=2,ω=2000 r·min-1工况条件与几何参数下,方向性倾斜微孔动压效应并不具有优势,以W=1600 N时为例,此时动压效应:方形孔>三角形孔>圆形孔>矩形孔>椭圆形孔>菱形孔,方形微孔端面平衡基础膜厚相较于菱形微孔端面增加9.3%。
2) 转速影响
图8所示为转速对6种孔型端面润滑特性的影响。随转速在250~10000 r·min-1范围内变化,平衡基础膜厚、摩擦转矩与摩擦系数变化相似,呈现逐渐增加趋势,尤其转速低于1000 r·min-1,曲线增长幅值变化明显,之后趋于缓慢。而流体流量随转速变化基本呈现线性增加趋势,区别在于,对于方向性倾斜微孔,椭圆形、菱形、矩形,转速越大,端面剪切作用越强,方向性微孔导流作用越明显,结果造成流体流量快速增加;而对于圆形、方形、三角形,流量数值较小,增加缓慢。
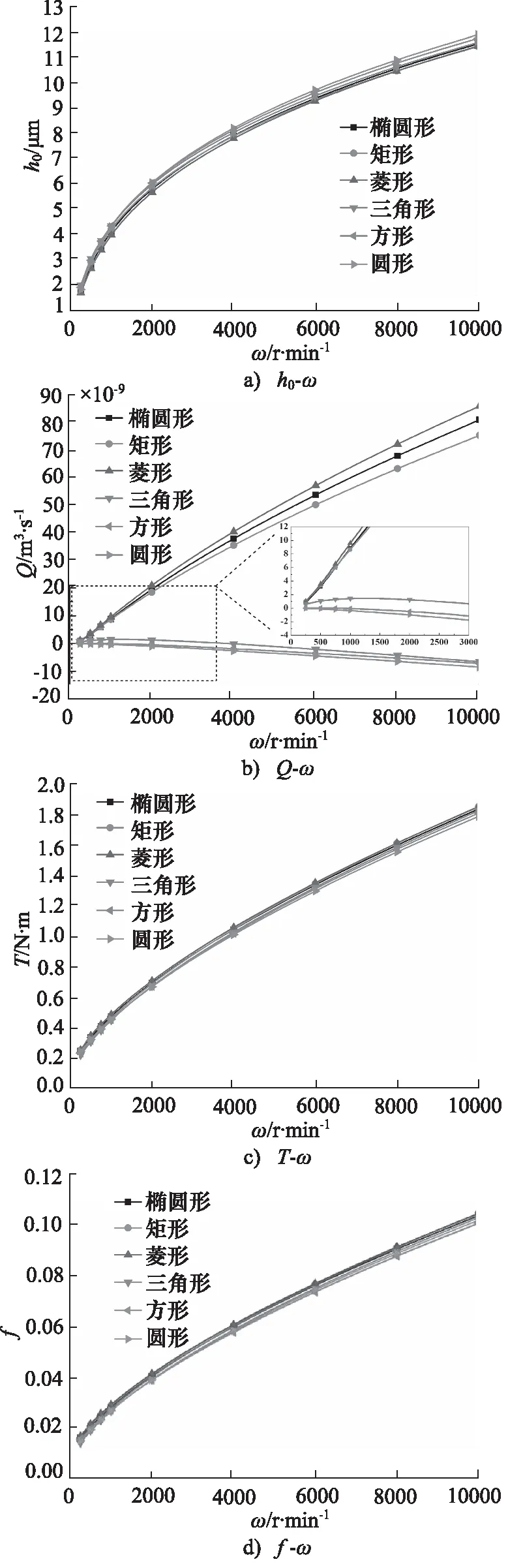
图8 转速对润滑特性影响(hd=4 μm, β=60°,λ=2,W=800 N)
对比六种孔型结构发现:无边界压差环境下,随转速变化,不同微孔的动压效应与摩擦特性相似,在ω=10000 r·min-1,圆形孔动压效应最强,相较于最弱的矩形孔,平衡基础膜厚增加4.0%,而摩擦转矩与摩擦系数较矩形孔也仅分别降低3.5%和3.8%。
2.3 结构参数影响
1) 孔深影响
孔深对微孔端面润滑特性影响如图9所示,随孔深的增加,平衡基础膜厚先增后减,在4~8 μm范围内获得最大值,说明在该深度取值范围内,微孔动压效应最强。相应地,随膜厚变化,流体摩擦力呈现相反的趋势,载荷不变情况下,摩擦系数呈现先减后增的变化规律,在4~8 μm范围内摩擦系数最低。
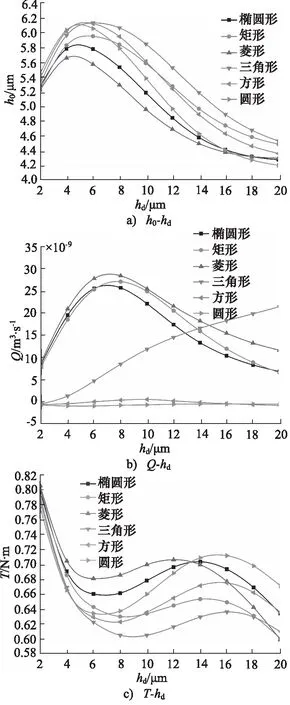
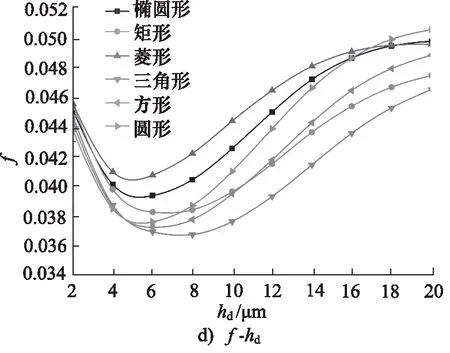
图9 孔深对润滑特性影响(β=60°,λ=2,ω=2000 r·min-1,W=800 N)
随孔深的增加,对于椭圆形孔、矩形孔、菱形孔,流体流量呈现先增后减趋势,最后趋于稳定,在6~8 μm范围内获得最大值;对于三角形孔,流体流量逐渐增加;对于圆形孔、方形孔,流体流量数值较小,且基本维持不变。综合考虑动压特征与摩擦特性,建议孔深取值为4~6 μm。
2) 倾斜角影响
微孔倾斜角对配合端面润滑特性影响如图10所示,随倾斜角的增加,圆孔端面性能参数不变,而倾斜微孔端面平衡基础膜厚逐渐减小,在0~20°膜厚最大,说明此时微孔动压效应最强。摩擦转矩与摩擦系数随倾斜角增加出现相似变化,呈现逐渐增加趋势,在0~20°达到最小,在90°达到最大。而流量变化呈现先增后减的趋势,流动方向与微孔长轴导流作用相关,在0°、90°附近流量最小,而在40°~60°附近流量最大,综合润滑性能变化情况,建议微孔倾斜角取值为 0~20°。
比较不同孔型结构,在β=0~20°范围内,椭圆微孔与矩形微孔动压效应最为显著,且摩擦系数、摩擦转矩较小,因此端面纹理设计时,椭圆微孔与矩形微孔优势更为明显。
3) 方向因子影响
润滑性能参数随微孔方向因子变化如图11所示,对于方向性倾斜微孔,方向因子增加,迫使孔型狭窄化,增强流体动压效应,局部压力峰值增强,但整体平均膜压降低,如图12所示,流体膜承载能力削弱,为平衡外加负载作用,平衡基础膜厚减小,同时,狭窄化孔型结构增强对流体引导作用,促使端面流量增加。另一方面,膜厚减小引起流体摩擦力增大,随方向因子增加,摩擦转矩与摩擦系数呈现增加趋势。
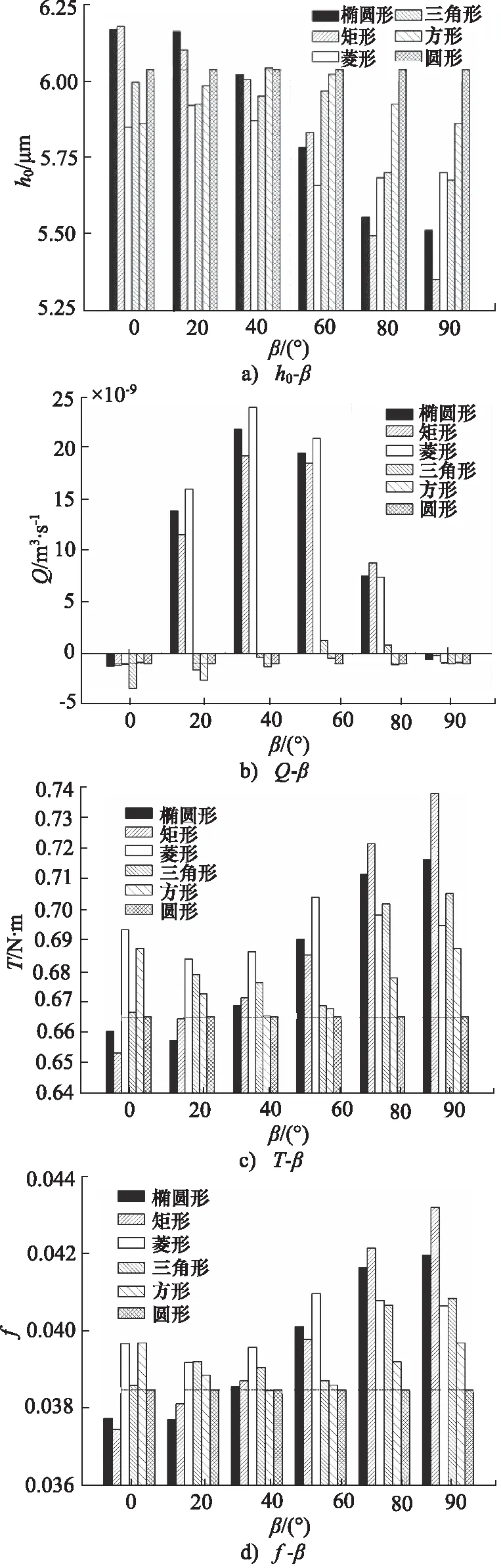
图10 微孔倾斜角对润滑特性影响(hd=4 μm,λ=2,ω=2000 r·min-1, W=800 N)
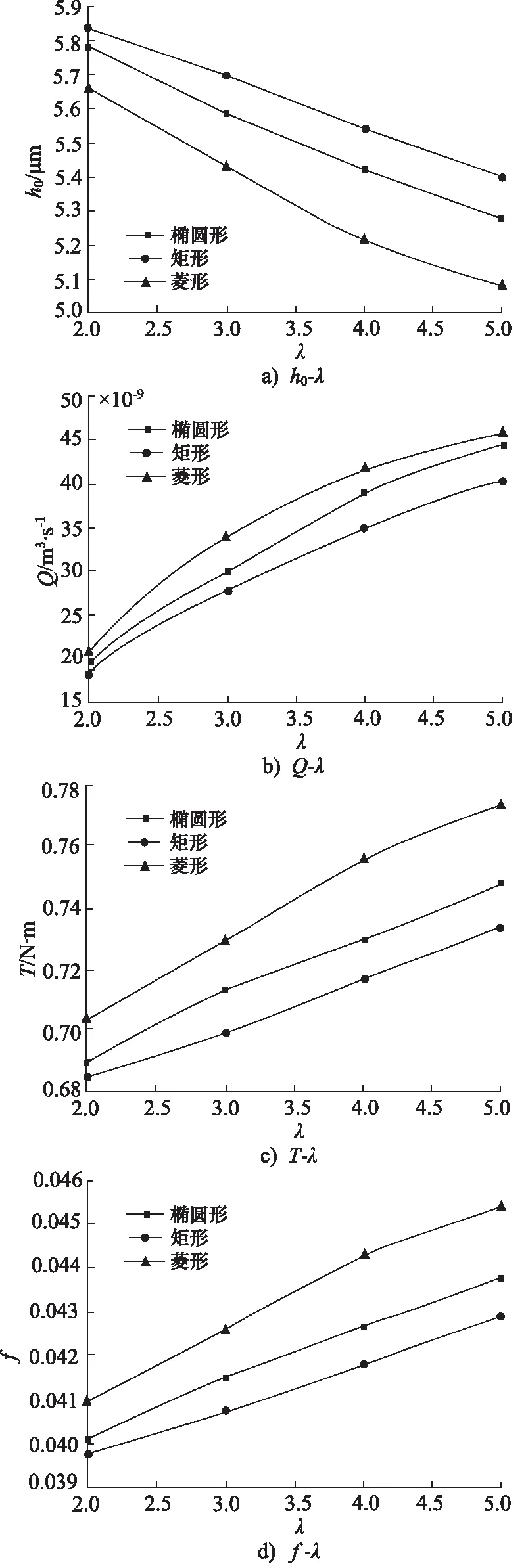
图11 方向因子对润滑特性影响(hd=4 μm, β=60°,ω=2000 r·min-1,W=800 N)
对于方向性倾斜微孔,在保证足够开启特性的同时,考虑流体流量、摩擦系数、摩擦转矩不宜过大,因此建议微孔方向因子取值为λ=2。
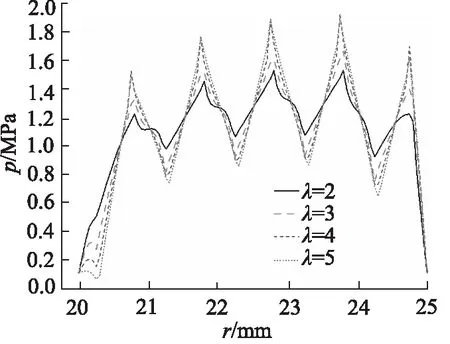
图12 椭圆微孔方向因子对计算区域中心轴线压力分布影响(hd=4 μm, β=60°,ω=2000 r·min-1,W=800 N)
3 结论
(1) 微孔方向性倾斜增加对流体的引导作用,促使流体介质沿椭圆微孔长轴方向流动,在微孔收敛间隙侧不断富集,形成动压效应,显著提升压力分布。弹性变形与流体膜厚度相对应,轴向压缩变形越大,润滑间隙尺寸越大,膜厚越厚。相比于平衡基础膜厚,端面变形对膜厚分布影响微弱,全膜润滑分析时可不予考虑;
(2) 操作工况与结构参数对不同孔型端面润滑特性影响明显。在微孔倾斜角β为0~20°范围内,椭圆微孔与矩形微孔动压效应最为显著,且摩擦系数、摩擦转矩较小,优势较为明显。在孔深4~6 μm、方向因子λ=2时,不同形状孔型结构润滑性能均可达到最佳效果。
