介质压缩性对高压柱塞泵间隙泄漏的影响
2020-07-14邹姜昆王忠凯刘银水赵申诞
邹姜昆,王忠凯,刘银水,赵申诞,董 婕
(1.兰州理工大学 能源与动力工程学院,甘肃 兰州 730050;2.华中科技大学 无锡研究院,江苏 无锡 214174; 3.无锡煤矿机械股份有限公司,江苏 无锡 214174)
引言
高压密封是各类高压柱塞泵关键控制因素之一,也是保证其可靠运行的关键部件[1-2]。目前,间隙密封已经广泛运用到许多苛刻工况中,如将间隙密封运用到高压液压缸中、液体火箭发动机的氢涡轮泵上以及高中压离心压缩机和汽轮机上等[3]。由于间隙密封属于非接触式密封,可大大降低密封面的摩擦磨损,延长密封件的使用寿命,并能提高往复柱塞件的线速度,降低柱塞泵的重量[4]。因此,对于各类高压径向柱塞泵而言,采用间隙密封结构形式将大大提高柱塞泵的综合性能与效率。
目前,国内外学者对间隙密封的设计与分析做了大量研究。KIRK R G等[5]利用有限元方法对环形密封的二维压力场与温度场进行分析,并采用非线性雷诺方程来考虑黏度与压力和温度的关系。DUAN W等[6]利用大流量模型对浮动环间隙密封进行静态与动态分析。周梓荣等[7]对缝隙间隙下液体的不同流动状态的计算方法进行了研究,并给出了流动状态的判定依据。蒋俊等[8]利用CFD技术对间隙密封液压缸的泄漏量进行了分析,分析了其不同缝隙间隙与不同速度下的泄漏量关系。胡前茅等[9]对变间隙密封的密封间隙进行仿真实验,实现对压力、密封间隙、活塞运动位移量的数据采集和数据处理。焦龙飞等[10]研究了油液压缩性对柱塞泵容积效率的影响。林静等[11]利用CFD对泵出口流量脉动进行计算,但是将工作介质当做不可压缩流体。
目前对于以水为介质的可压缩性对高压柱塞泵间隙泄漏与容积效率的影响的研究很少。然而,对于高压径向柱塞泵,其压力高,水的压缩性对柱塞组件泄漏量与容积效率影响不可忽略。因此,结合高压径向柱塞泵的结构尺寸,采用动态密封长度进行设计。首先对柱塞往复一周的动态密封长度与速度进行积分,得到不同缝隙间隙与压力下柱塞泵泄漏量与容积效率。然后利用Fluent分析不同压力下水的可压缩与不可压缩两种状态下对柱塞组件泄漏量与容积效率的影响程度。最后得到其对柱塞组件泄漏量与容积效率的影响规律,为高压径向柱塞泵间隙密封的设计提供了理论依据。
1 柱塞组件泄漏量与容积效率分析计算
1.1 柱塞组件数学模型
在分析高压径向柱塞泵高压密封泄漏之前,首先要知道其高压处柱塞组件的运动学关系并建立数学模型。高压径向柱塞泵柱塞组件系统包括曲轴、连杆、柱塞、柱塞套等主要零部件,其工作原理为:通过曲轴旋转带动连杆运动,连杆带动滑块与柱塞做往复直线运动。其中高压密封在柱塞与柱塞套处,其间隙密封结构形式如图1所示。
通过间隙密封结构形式,建立如图2所示的柱塞组件数学分析模型。规定以轴伸端往里看曲轴顺时针方向旋转,同时规定以x轴负方向开始计时,此时柱塞组件处于最左端位置,并规定此时柱塞组件的相对位移为0。因此,柱塞与柱塞套以初始时刻密封长度开始相对运动。其中θ为曲轴旋转t时刻时的任意转角,rad。表1为柱塞组件系统几何参数。
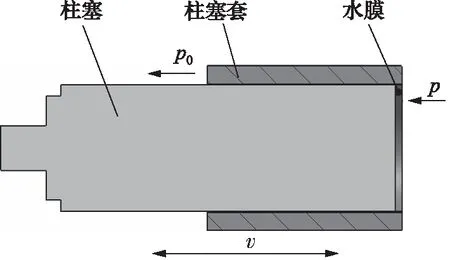
图1 间隙密封结构形式
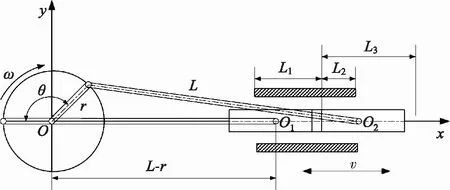
图2 柱塞组件数学模型
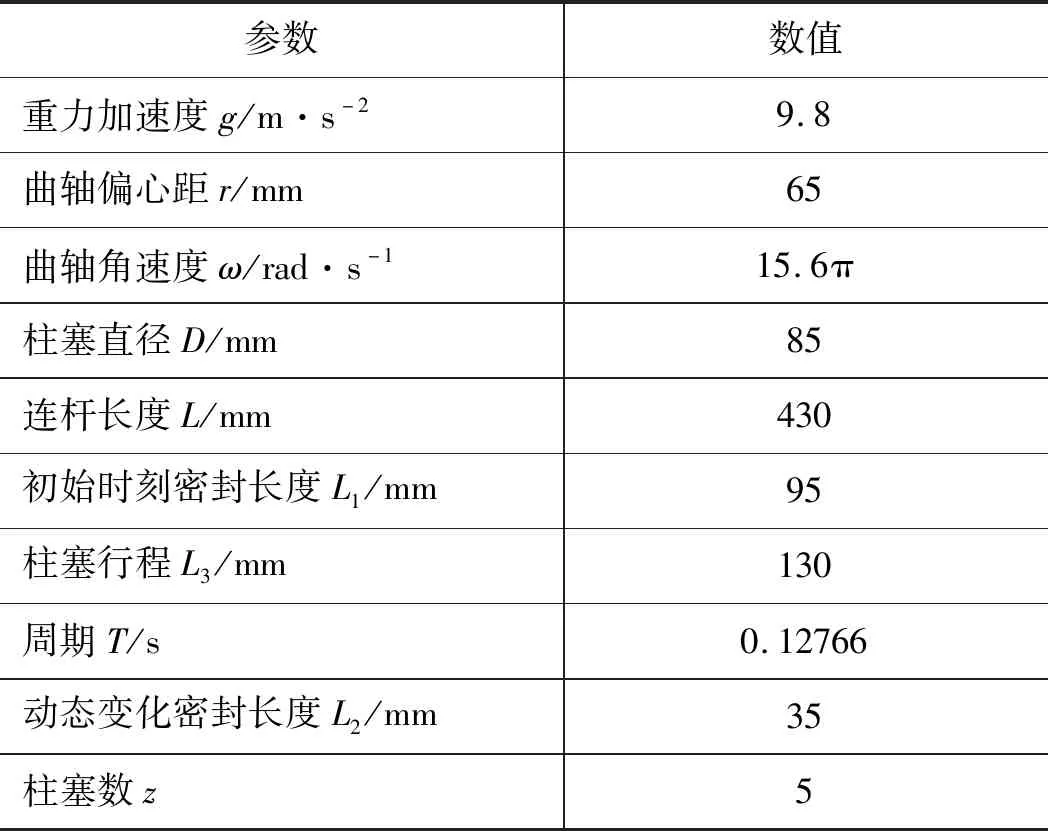
表1 柱塞组件系统几何参数
1.2 柱塞组件运动学分析
通过对柱塞组件数学模型的分析可以得到柱塞组件在曲轴旋转1周的过程当中的运动学方程:
规定以x轴负方向开始计,因此柱塞组件的相对位移可表示为:
通过对位移求导可得柱塞组件的速度:
(2)
其中,曲轴旋转角度θ与曲轴旋转角速度ω之间的关系为:
θ=ωt
(3)
通过对柱塞组件运动学分析可以得到柱塞在曲轴旋转一周的过程中的运动学关系。下面将基于此分析柱塞与柱塞套动态密封泄漏。
1.3 高压密封动态泄漏分析
相对速度为v的柱塞与柱塞套之间形成微小间隙的间隙密封,柱塞与柱塞套之间的缝隙流动为层流流动状态,柱塞与柱塞套之间泄漏由柱塞两端的压差与柱塞与柱塞套的相对运动形成的压差流与剪切流所造成[12]。考虑到实际运行过程中,柱塞与柱塞套之间存在偏心倾斜问题,在柱塞套中心处,柱塞与柱塞套处于同心,在柱塞套两端处,柱塞与柱塞套处于完全偏心,因此,通过积分可以得到层流流态泄漏量基本计算公式为[13]:
(4)
式中,μ为水的动力黏度,Pa·s; Δp0为压差,MPa;H为柱塞与柱塞套之间的单边缝隙间隙,mm。
考虑到间隙流动的黏性效应与进出口起始段的惯性效应[14],以式(4)作为基本计算公式,通过微小流体动能变化并积分可得惯性流动的总功率为:
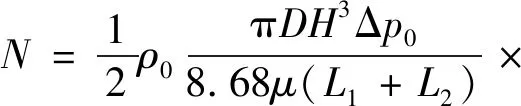
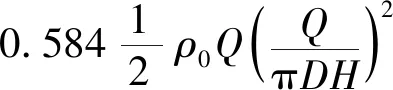
(5)
通过总功率可得进出口惯性流动的压力降,并结合黏性流动压力降可得总压力降为:
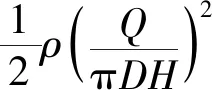
(6)
通过式(6)可计算得出一元二次方程的根,得到流量计算公式为:
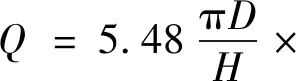
(7)
考虑到水的可压缩性,由于水的弹性模量和密度会随压力发生变化,因此,在考虑了水的体积弹性模量后,由连续性方程和运动方程可得[15]:
(8)
式中,K为水的体积弹性模量,MPa;p为流体进口压力,MPa;p0为大气压力,MPa;ρ0为常温常压下流体密度,kg/m3;V为流体体积,m3。
其具体数值如表3所示。在缝隙流动中,介质压缩后产生容积损失,在缝隙间隙体积不变的情况下,由于缝隙内流体的密度发生变化,则缝隙内液体质量相应增加或减小,其变化比例为:
(9)
由于通过柱塞组件运动学分析模型可以知道其1个周期内的动态密封泄漏分为三个过程,第一个过程是由于压差流与剪切流造成,且密封长度与速度随时间变化。第二个过程是由于压差流与剪切流造成,且密封长度为定值,速度随时间变化。第三个过程是由剪切流造成,压差流为0。并规定柱塞运动速度方向与压差降方向相同时剪切流为正,相反时剪切流为负。结合式(7)~式(9),可得在考虑柱塞位移变化、速度变化、柱塞与柱塞套倾斜、流体黏性效应与惯性效应和介质压缩性后修正的缝隙流动泄漏量计算公式为:
(10)
式中,t2为密封长度变化所需时间,s;t3为半个周期所需时间,s;t4为一个周期所需时间,s。
其具体时间参数如表2所示。

表2 动态泄漏时间参数 s
由式(10)可以得到单个柱塞动态泄漏曲线如图3所示。
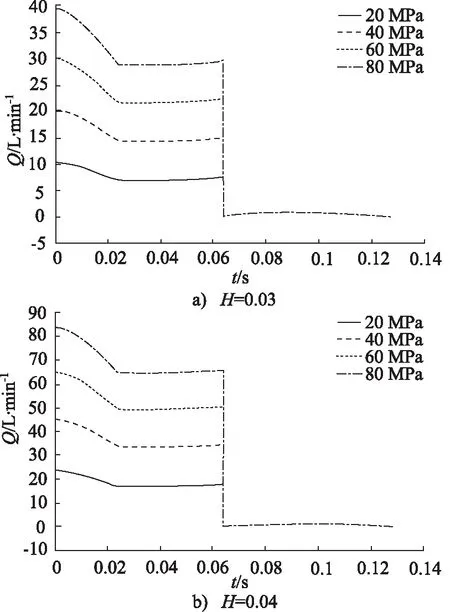
图3 不同压力下单个柱塞动态泄漏曲线(20 ℃)
由动态泄漏曲线可以看出,在第一个过程中,泄漏量下降较快,因为此时密封长度与柱塞运动速度都在增加。在第二个过程与第三个过程中,泄漏量变化只与速度变化有关。通过对单个柱塞动态泄漏曲线在柱塞运动1周时间内进行积分可以得到单个柱塞处于层流流动状态时其运动1周的泄漏量计算公式:
通过曲轴的转速可以得到单个柱塞组件在每分钟的泄漏量,由此可以得到5个柱塞组件每分钟总的泄漏量为:
Q1=znQ0
(12)
由径向柱塞泵理论流量计算公式:
Q2=0.25D2πL3zn
(13)
可以得到径向柱塞泵的容积效率为:
(14)
其中,n为曲轴转速,r/min。通过以上计算公式并利用MATLAB编程可以得到不同压力下柱塞泵的泄漏量与容积效率如图4所示。
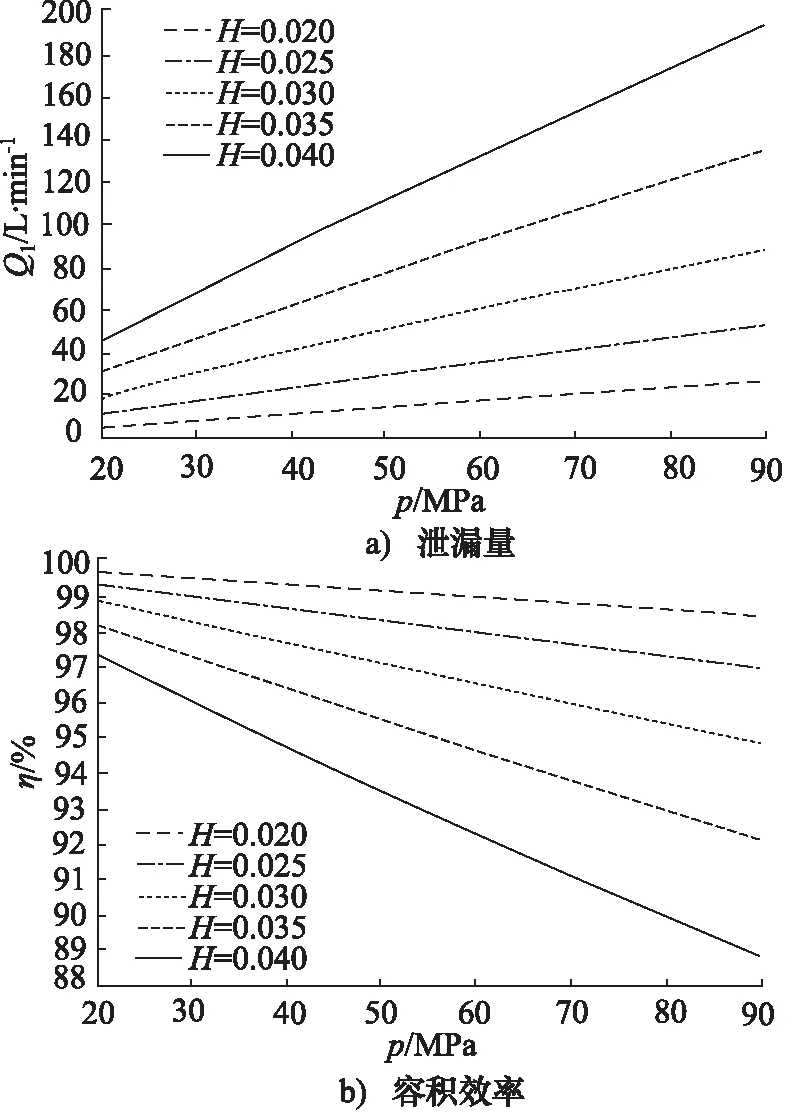
图4 不同压力下泄漏量与容积效率曲线(20 ℃)
通过图4可以得到,随着压力的升高,柱塞组件泄漏量呈线性增加,容积效率呈线性减小。且随着缝隙间隙的增大,其泄漏程度越大。当缝隙间隙为0.02 mm时,压力从20 MPa上升到90 MPa,泄漏量从6.13 L/min上升到27.38 L/min,容积效率从99.65%下降到98.42%。当缝隙间隙为0.04 mm时,泄漏量从47.43 L/min上升到193.30 L/min,容积效率从97.26%下降到88.85%。
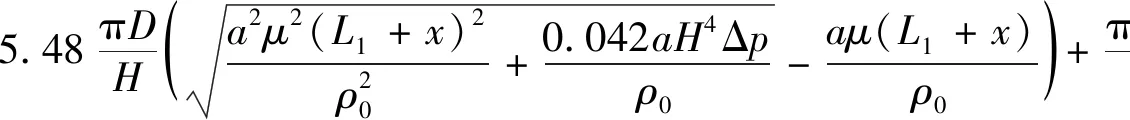
(11)
2 柱塞组件CFD流场仿真分析
2.1 流场仿真模型
建立柱塞组件的流场仿真模型,通过仿真计算研究水的可压缩性对高压径向柱塞泵泄漏量与容积效率的影响。首先建立柱塞与柱塞套、缝隙水膜的三维模型并进行简化,并将三维实体模型导入到ANSYS Workbench中的Mesh模块,在Mesh模块中选择自动生成ICEM模块,并打开ICEM界面,在ICEM界面中进行结构网格或非结构网格的划分。在ICEM中,六面体网格划分采用由顶至下和自顶向上的“雕塑”方式,可以产生多重拓扑块的结构化网格。将计算模型进行建块,设置生成3个Multizone模块,将Element Size设置成2.0 mm,最后得到的网格节点数为1386050个,网格单元数为321446个,网格类型为六面体网格,其有限元三维模型如图5所示,模型中水膜的厚度设置为0.025 mm。
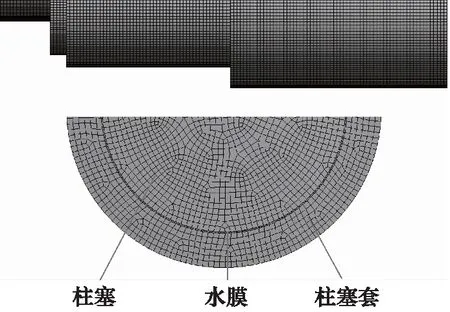
图5 柱塞组件有限元三维模型
2.2 仿真参数设定
由于水的弹性模量和密度会随压力发生变化,因此,在考虑了水的体积弹性模量后,由式(8)和式(9)可得其密度变化规律。其设定的流体仿真参数如表3所示。

表3 流体仿真参数
2.3 仿真结果分析
根据柱塞运动规律,运用Fluent中的动网格对柱塞往复运动进行模拟,流体水膜进出口边界条件为压力边界条件。其中进口压力分别设定为20, 30, 40, 50, 60, 70, 80, 90 MPa,出口压力为大气压。仿真结束后得到不同进口压力下流体水膜的压力云图如图6所示。

图6 不同进口压力时流体水膜压力分布云图
由图6可以看出,在缝隙长度内,流体水膜的压力呈梯度分布,并从进口到出口其压力逐渐下降。通过Fluent后处理模块对图形数据进行计算处理,得到不同压力下流体水膜在可压缩与不可压缩时高压径向五柱塞泵的泄漏量,如表4所示。通过表4可以得到其压缩泄漏量与压缩泄漏比重η1。
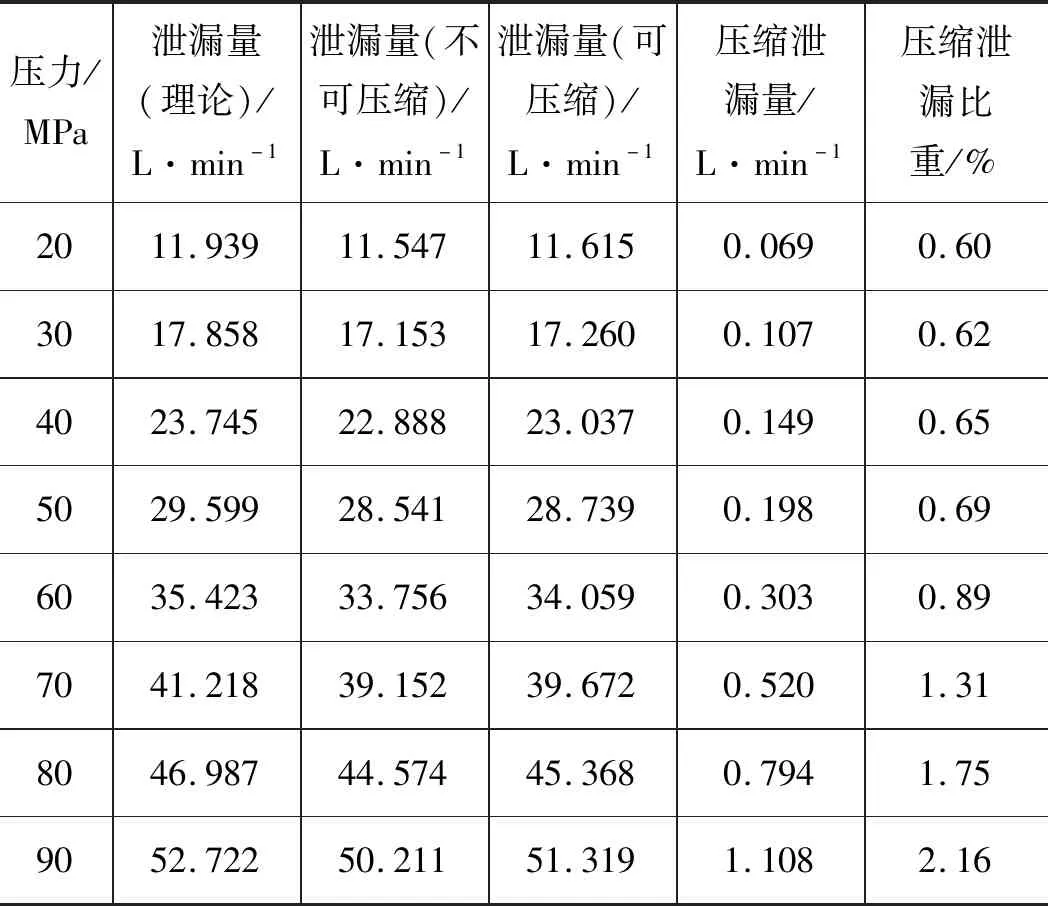
表4 不同压力下泄漏流量(温度20 ℃、缝隙间隙0.025 mm)
通过表4可以看出,随着压力的增大,由于压缩产生的泄漏量不断增大,压力从20~90 MPa变化时,其压缩泄漏量从0.069 L/min增大到1.108 L/min。图7为可压缩与不可压缩两种状态下其泄漏量与容积效率与理论值之间的对比,图8为压缩泄漏比重随着压力增加的变化趋势。
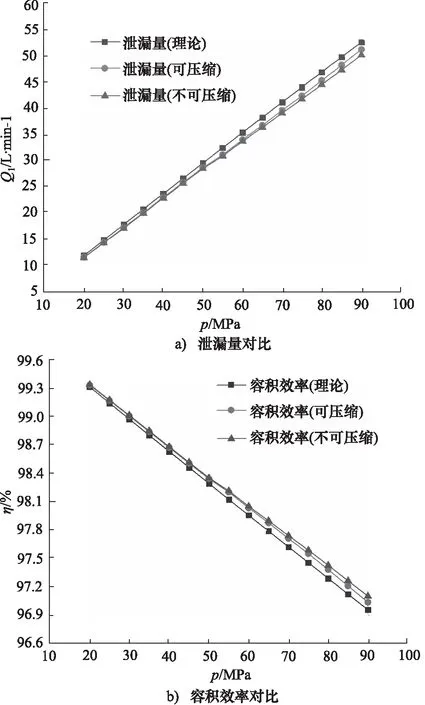
图7 可压缩与不可压缩对比曲线
由图7可知,通过Fluent仿真得到的高压径向柱塞泵的泄漏量略小于理论数学模型计算的泄漏量,其误差在2.66%~4.09%之间。当压力从20 MPa增加到90 MPa时,其理论容积效率从99.311%减小到96.959%,可压缩介质容积效率从99.334%减小到97.103%。当考虑介质压缩性时,其泄漏量比不考虑介质压缩性时的大,这是由水的压缩性引起压缩容积损失而造成的,且随着压力的增大,其程度不断增大。因此,在考虑了水的压缩性后,其泄漏量与容积效率更接近实际情况。从图8可以得到压缩泄漏比重随压力的增大呈非线性变化,当压力小于50 MPa时,压缩泄漏比重增加缓慢;当压力超过50 MPa时,其曲线斜率增大,此时介质压缩性对泄漏量与容积效率产生较大影响;当压力从50 MPa增加到90 MPa时,其压缩泄漏比重从0.69%增加到2.16%。
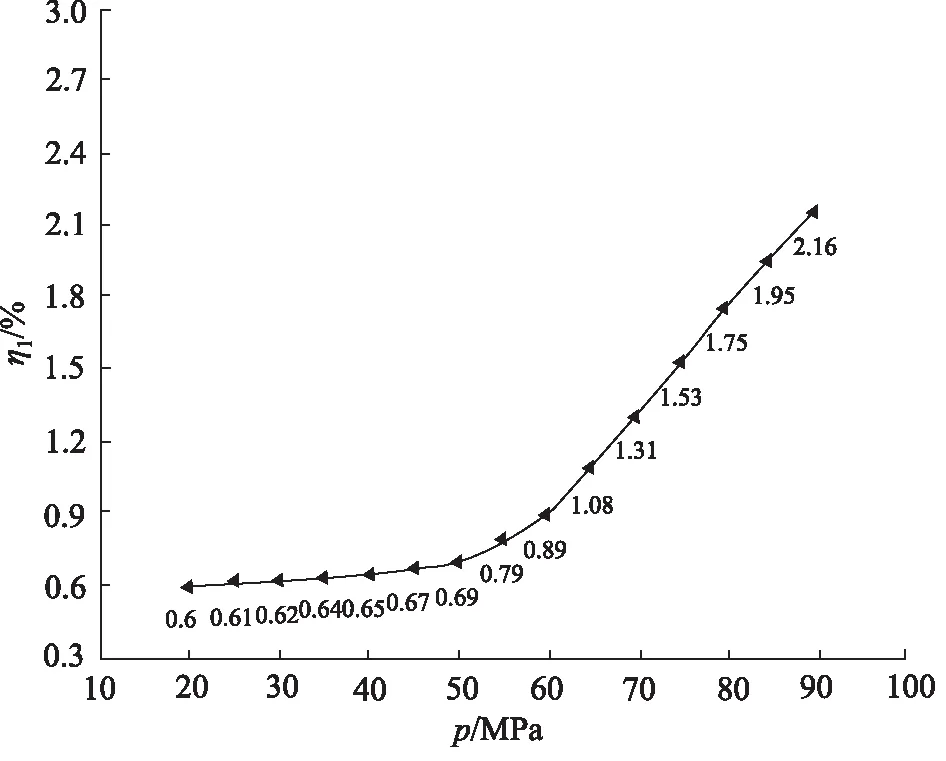
图8 压缩泄漏比重
3 结论
文章对水的压缩性对高压柱塞泵间隙泄漏的影响进行了理论与仿真研究。首先通过理论计算得到介质可压缩性的泄漏量与缝隙间隙和压力的变化规律,然后通过仿真计算得到了不同压力下水的压缩泄漏比重。通过理论计算与仿真,我们可以得出以下结论:
(1) 通过理论计算,可得在考虑柱塞位移变化、速度变化、柱塞与柱塞套倾斜、流体黏性效应与惯性效应和介质压缩性后修正的缝隙流动泄漏量计算公式。随着压力升高,间隙密封的泄漏量呈线性增加,容积效率呈线性减小,并且随着缝隙间隙的增大,其泄漏程度不断增大,即其曲线斜率越大;
(2) 通过Fluent仿真计算得到在考虑介质压缩性后的间隙密封泄漏量与理论计算泄漏量的误差在2.66%~4.09%之间,验证了数学模型的正确性;
(3) 通过计算与仿真,可以得到当考虑水的压缩性后,其压缩泄漏比重随着压力的增大呈非线性增大,当压力从50 MPa增加到90 MPa时,其压缩泄漏比重从0.69%增加到了2.16%。因此,对于高压径向柱塞泵,当工作压力较高时,其介质可压缩性影响较大。
