油茶籽压榨过程中的应力应变特性研究
2020-07-14李正文宋少云曹梅丽冯新东
李正文,宋少云,2,郑 晓,曹梅丽,2,尹 芳,周 劲,2,冯新东
(1.武汉轻工大学 机械工程学院,武汉 430023; 2.湖北省粮油机械工程技术研究中心, 武汉 430023)
油茶籽油是我国最古老的木本食用植物油之一,我国是世界上山茶科植物分布最广的国家,是世界上最大的油茶籽油生产基地[1]。油茶籽油具有预防和治疗心血管疾病、延缓衰老、增强免疫系统功能、抗癌等作用,是一种食用与医疗兼优的良品油[2-3]。压榨法是油茶籽制油的常用方法。吴雪辉等[4]采用3种压榨方式获得油茶籽油,使用灰色关联法和主成分分析法综合分析得出:古法压榨获得的油茶籽油品质最好,营养价值最高。熊平原等[5]设计了一套轻巧型油茶籽脱壳装置,并利用ADAMS对油茶籽运动轨迹及破壳受力进行了运动仿真分析。上述研究多关注的是油茶籽的压榨效果,而尚未对压榨的应力应变关系进行深入研究。但对于其他油料作物,则有学者对其压榨力学特性有较为深入的研究。何东平等[6]确立了花生在压榨过程中出油率与压榨压力的经验公式。郑晓等[7-8]采用川北方程建立了花生、大豆、芝麻等压榨的应力应变的关系模型,对于油菜籽和菜籽仁的出油压力和出油率的关系也进行了系统研究。
为了深入了解油茶籽在压榨过程中的应力应变关系,本文以湖北省的某种油茶籽为压榨对象,使用自制的侧限排油柱塞式压榨装置,分别对3种质量(20、30、40 g)的油茶籽进行了4种加载速率(0.01、0.02、0.04 kN/s和0.06 kN/s)的压榨,得到了其应力应变曲线。使用川北方程进行了曲线拟合,得到了4种加载速率下的应力应变关系的数学模型。建立的数学模型可以作为有限元仿真分析的底层数学公式,可为榨油仿真奠定基础。
1 材料与方法
1.1 试验材料
油茶籽产自于湖北省,皆为剥壳油茶籽,含水率7.5%、含油率29.2%。
试验装置主要由一台液压式材料压缩试验机(简称压缩试验机)、与之配套的控制系统SmartTest以及一个自制的侧限排油柱塞式压榨装置(简称压榨装置)组成[8],如图1所示。压榨装置放置在压缩试验机的工作台和上压头之间,而上压头固定。在SmartTest程序的控制下,工作台受液压驱动而上行以压缩压榨装置的活塞,从而完成对压榨室内油茶籽的压榨。

注:1.压缩试验机;2.控制系统;3.压榨装置。
图1 油茶籽压缩试验装置
1.2 试验方法
称取指定质量(20、30、40 g)的油茶籽,装入压榨室内;将压榨装置置于材料压缩试验机上,利用压缩试验机控制系统中的SmartTest程序控制加载装置对压榨装置进行加载,以恒定的加载速率加载到指定的压力水平,然后卸载;此时SmartTest会记录力-时间、变形-时间、位移-时间、应力-时间、应变-时间、力-变形、力-位移、应力-应变等试验曲线,并保存下所有试验数据。为了考察不同加载速率对于压榨的影响,本试验选择4种加载速率:0.01、0.02、0.04 kN/s和0.06 kN/s。压榨试验在常温18℃下进行。
2 结果与讨论
2.1 应力应变试验结果
40 g油茶籽在不同加载速率下的部分应力应变结果如表1所示。

表1 40 g油茶籽不同加载速率的应力应变结果
40 g油茶籽在加载速率0.04 kN/s的应力应变曲线如图2所示。
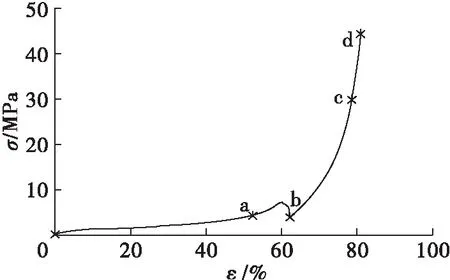
图2 0.04 kN/s加载速率下40 g油茶籽的应力应变曲线
不同加载速率下的油茶籽应力应变曲线如图3~图5所示。
为了考察在大量出油阶段加载速率对出油率的影响,将图3中大量出油阶段之前的部分放大,结果如图6所示。
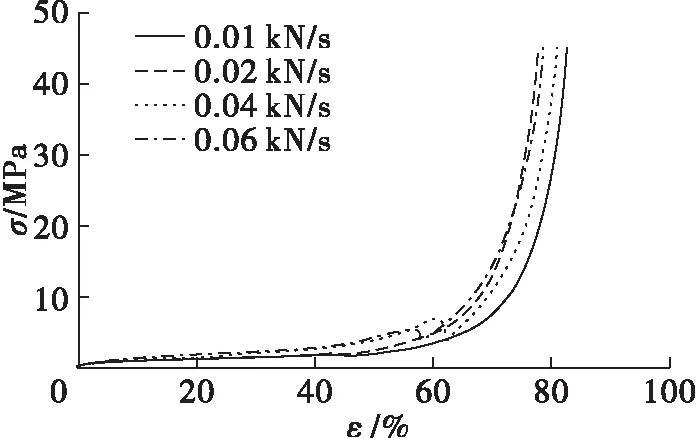
图3 不同加载速率下40 g油茶籽的应力应变曲线

图4 不同加载速率下30 g油茶籽的应力应变曲线

图5 不同加载速率下20 g油茶籽的应力应变曲线

图6 不同加载速率下突变现象阶段的应力应变曲线
2.2 应力应变试验结果分析
值得注意的是,在试验过程中,以下几种情况的试验均失败了:情况1(40 g的油茶籽,加载速率为0.1 kN/s),情况2(30 g的油茶籽,加载速率为0.06 kN/s),情况3(20 g的油茶籽,加载速率为0.04 kN/s)。此处的试验失败是指当加载速率过快超过某个值以后,试验会在很短时间内完成,并且此试验会呈现出油量极少的情况,与前面的试验完全不成比例,出现这种情况的原因可能是加载速率过快,油来不急排出所致。
试验发现,不同质量的油茶籽对应力应变关系的影响可以忽略。同时质量越大,系统所产生的误差越小,被误差影响的概率越小,故而主要对40 g的油茶籽进行研究即可。
为了对油茶籽的压榨应力应变曲线有一个更清晰的认识,取一种各种特征特别明显的典型工况(40 g的油茶籽,加载速率为0.04 kN/s)的应力应变曲线进行分析和研究(如图2所示)。
从图2可以发现,油茶籽压榨过程中的应力应变总体上分为4个阶段:①压缩阶段(即0a)。此阶段基本上是一条斜率较小的倾斜线段,此时油茶籽被逐渐压紧,发生轻微的塑性变形。②压实阶段(即ab)。此阶段开始呈现较陡的非线性变化,并伴有突变现象,此时油茶籽被压得十分密实,发生剧烈的塑性变形,开始少量出油,颗粒之间的空隙基本已全被填满。③出油阶段(即bc)。此阶段油料逐渐变为饱和多孔介质状态,开始大量出油,这是压榨法出油效率最高的阶段。④强化阶段(即cd)。这个阶段应力应变曲线变得陡峭,斜率变得很大,油料应变硬化很大,物料结构紧密,虽然压力直线上升,但是油料变形很小,出油效率大大降低。
从图3~图5可以发现,加载速率对其应力应变关系的影响明显,应变总体上随着加载速率的减小而增加。根据渗流理论,液体在多孔介质中的渗流具有明显的时间效应,液体渗流量与渗流时间成正比。加载速率越小,渗流时间越长,渗流量越多,变形也就越大。因此,应变将随着加载速率的减小而增加。此外,加载速率为0.04 kN/s的40 g油茶籽、加载速率为0.06 kN/s的40 g油茶籽、加载速率为0.02 kN/s的20 g油茶籽的应力应变曲线均出现了瞬时突变。笔者认为瞬时突变之前为压实阶段,在这个阶段内几乎不出油;当加载速率较大的时候,颗粒之间会留下一定的缝隙不会被完全填满,当试验力达到一定的值后,会瞬时把这些遗留的空隙填满,故而产生了突变现象。
从图6可以发现,在同一应力水平下,图中的水平横线从左往右依次穿过的是0.06、0.02、0.04、0.01 kN/s,可以发现加载速率0.04 kN/s的应变反而比0.02 kN/s大。这意味着:并不是加载速率越小,应变就越大,从而出油率就越大。产生此现象的原因可能是:虽然压榨过程需要足够的时间以保证油脂充分排出,但是时间过长,也会使流油通道变窄甚至闭塞。因此,每一种油料压榨时都有一种合适的加载速率。该速率既不能太快,从而使得油不能及时排出;也不能太慢,使得流油通道变狭窄。对于本文所考察的油茶籽而言,0.04 kN/s是一个合适的加载速率,既保证了一定的压榨效率,也保证了合适的出油量。
2.3 应力应变数学模型的建立
为了得到油茶籽在侧限排油的一维压榨应力应变的数学模型,用川北方程进行推导拟合,得到
(1)
式中:a、b为常数。
将表1中对应每一个加载速率,任选两行(本文选择的是10、20 MPa两行)数据代入式(1),得到两个二元一次线性方程,联立求解得到常数a、b的值,如表2所示。

表2 待定系数a、b值
将表2中的a、b代入式(1)中,就得到一定加载速率下的应力应变关系数学模型。为了验证所建立的数学模型的正确性,将数学模型所对应的曲线与试验值进行比较,结果如图7~图10所示。
从图7~图10可以看出,实测的数据散点都在建立的数学模型曲线周围波动,说明使用川北方程所建立的数学模型是比较准确的。

图7 加载速率为0.01 kN/s的应力应变模拟
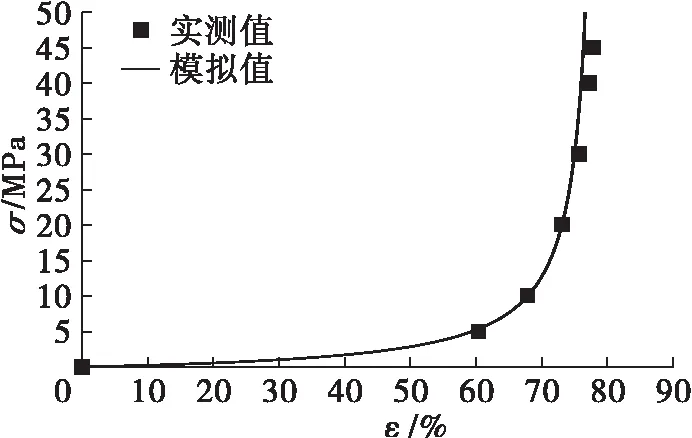
图8 加载速率为0.02 kN/s的应力应变模拟
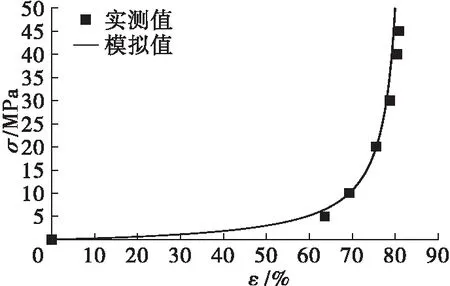
图9 加载速率为0.04 kN/s的应力应变模拟

图10 加载速率为0.06 kN/s的应力应变模拟
3 结 论
(1)油茶籽压榨过程中的应力应变曲线可分为4个阶段:压缩阶段、压实阶段、出油阶段、强化阶段。
(2)总体上加载速率越小,同一应力水平下的应变越大,出油率越高;但是,加载速率为0.04 kN/s的应变反而比加载速率为0.02 kN/s的应变大,意味着0.04 kN/s是一个合适的加载速率,既保证了一定的压榨效率,也提供了较高的出油率;此外,不同质量的油茶籽对应力应变关系的影响可以忽略。
(3)基于川北方程建立了油茶籽在侧限排油的一维压榨应力应变的数学模型,结果表明,川北方程能够较好地拟合油茶籽的压榨应力应变曲线,为榨油过程的有限元仿真分析提供了基础。
