砂土中陆地风电空心锥形基础水平承载力的影响因素分析
2020-07-14李大勇房兆晓张雨坤王超慧
李大勇,房兆晓,张雨坤*,王超慧
(1.山东科技大学山东省土木工程防灾减灾重点试验室,青岛 266590;2.福州大学土木工程学院,福州 350108)
中国陆地风电场正处于快速建设时期。在风电场成本构成中,基础建造安装费用约占总成本的13%。在确保风电基础具有足够承载力前提下减少基础开挖量、混凝土和钢筋等用量,可以降低基础工程造价。陆地风电常见的基础形式有重力式基础、岩石锚杆基础、梁板式基础等,其中圆形重力式基础应用最为广泛[1]。
陆地风电塔架基础在服役期间受到自身与上部结构重力作用,以及风荷载产生的水平力和倾覆力矩作用,而水平力和倾覆力矩远大于竖向荷载,为基础的主控荷载[2]。中外学者对陆地风电基础的承载特性进行了大量研究。罗强等[3]通过离心模型试验,研究了圆形和方形浅基础在密砂地基中的承载力和变形特性,探讨了基础形状的变化对地基承载力系数的影响;刘梅梅等[4]采用理论推导和数值模拟相结合的方法,对圆形重力式基础极限荷载作用下基础与地基相互作用规律进行了研究,讨论了基础刚度判别标准并修正了柔性基础最大基底反力计算公式;李亮等[5]对地基极限承载力上限解析解进行推导,发现持力层强度不受基础面积大小的影响,而地基承载力大小随基础面积的增加而增大;阳平等[6]采用矩阵传递法研究了水平荷载作用下倾覆力矩、基础尺寸、地基变形模量对基础倾斜的影响,认为增大基础尺寸能显著增强基础的抗倾覆性能;李东轩等[7]通过数值模拟的方法,讨论了不同跨高比、刚度比对岩基扩展基础抗剪性能的影响规律;Wakil[8]通过模型试验探究了砂土地基相对密实度和基础尺寸对圆形重力式基础水平承载特性的影响,并认为基础在水平荷载作用下的破坏形式为转动破坏;Garakani等[9]对单调加载条件下基础埋深和土体内摩擦角对基础承载力的影响进行研究,并推导出基础承载力的计算公式;Matos等[10]为了提高土体的抗倾覆能力和基础的刚度,优化了传统重力式基础的形式,采用微钢桩加固基础;Mohamed等[11]对一种改良型重力式基础的承载力进行了研究,得出该基础的承载力优于传统圆形重力式基础的结论;Cui等[12]对圆形重力式基础进行了现场试验,研究了基础的几何尺寸对抗拔承载力的影响。
另外,通过对许多陆地风电场现场调研发现,陆地风电塔架基础在建设中普遍存在的问题有土方开挖量大、开挖出的碎石废渣堆砌在周围影响陆地植被环境、钢筋混凝土用量大且成本占比高等问题。针对陆地风电基础建设的特点以及现有基础存在的问题,提出一种钢筋混凝土空心锥形陆地风电柔性基础[13-14]。该基础为空心锥形结构,空心内回填基坑开挖产生的渣土,上下顶板及侧壁由钢筋混凝土浇筑而成,侧壁和基坑之间铺设素混凝土垫层和废旧轮胎橡胶颗粒层。
与传统的圆形重力式基础(以下简称圆形基础)相比,锥形基础具有诸多优点。采用空心结构,并将基坑开挖的废渣土回填,可减小钢筋混凝土的用量,节省基础造价;基础采用锥形结构,增加了基础侧壁与土体的接触面积,可以调动更多的土体抵抗基础所受的水平荷载,有利于提高基础的承载性能;将基坑开挖产生的废渣土充分利用,减少废渣土堆放对周围环境的影响,减少运送成本;铺设橡胶隔离层,可使基础与地基之间变为柔性接触,释放基础受到的巨大弯矩,提高基础的承载力和稳定性。
开展模型试验探究水平单调荷载作用下锥形基础的承载特性,分析了加载高度、加载速率、模型尺寸对锥形基础水平承载力的影响,并与相同质量和径高比的圆形基础的承载力进行了比较。
1 试验装置及土体制备
1.1 模型试验箱和基础模型
模型箱的尺寸为:长×宽×高=1 m×1 m×0.8 m,前期通过开展数值模拟证实该尺寸能消除边界效应的影响。
锥形基础模型为钢制材料,如图1所示。前期对相同质量,不同径高比的锥形基础进行有限元数值模拟,发现径高比D/H=5~6(D为基础上顶板直径,H为基础高度)时锥形基础水平承载力最高。据此加工了6个质量相同的基础模型,具体参数如表1所示,其中d为基础下底板直径。

图1 基础模型Fig.1 Foundation models

表1 基础模型尺寸Table 1 Dimensions of foundations
1.2 试验用砂及土体制备
试验砂土颗粒级配曲线如图2所示。砂土的平均粒径D50=0.9 mm,不均匀系数Cu=6.17,曲率系数Cc=1.63,表明砂土为级配连续且级配良好的中粗砂。
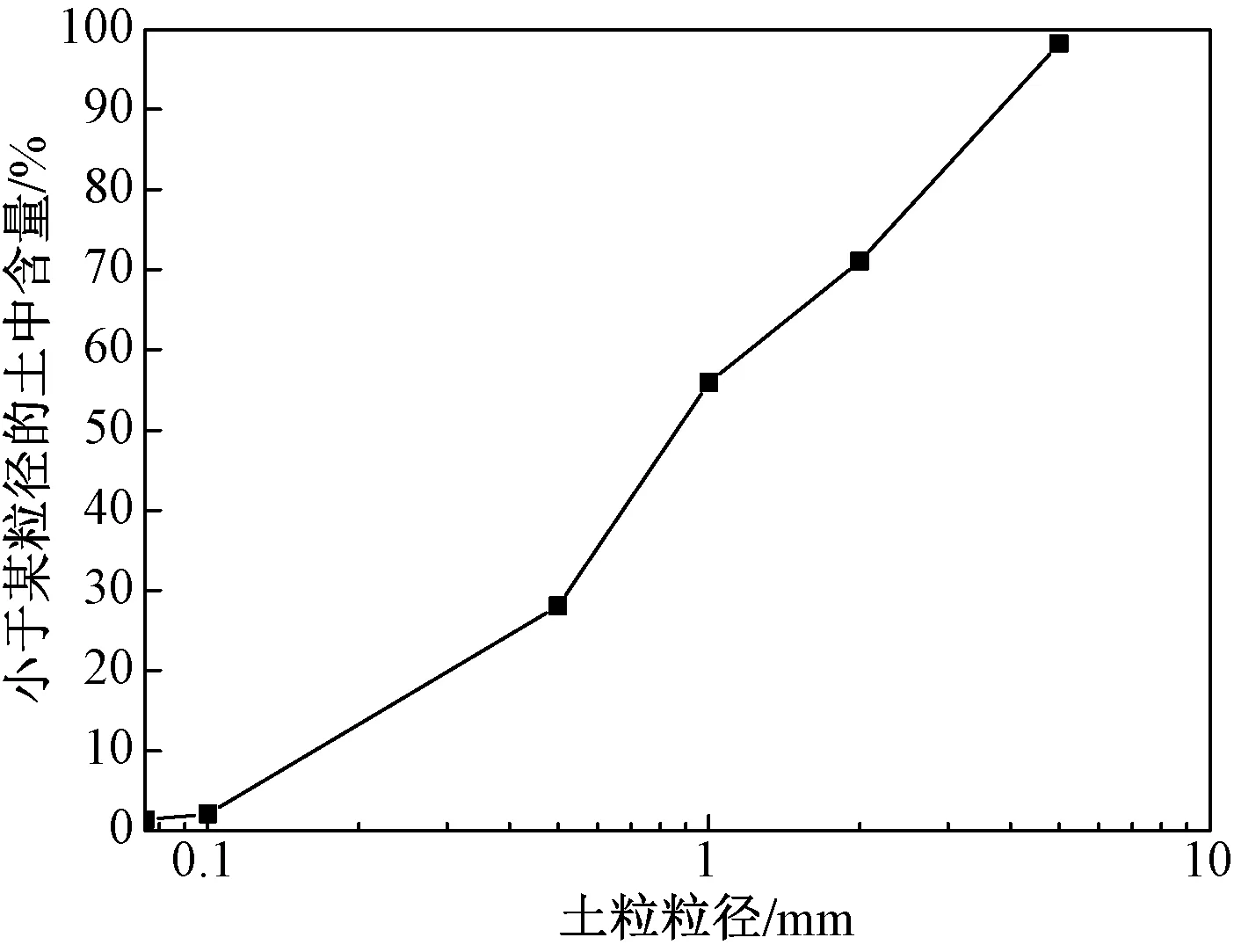
图2 颗粒级配曲线Fig.2 Particle size distribution curve
模型箱内砂土地基制备方法如下:在基础底部铺设土工布;自模型箱底部向上均匀播撒5 cm厚砂土,将砂面刮平并夯实;重复上述步骤直至砂土层厚度达到60 cm,静置24 h后开始试验。
1.3 试验装置与流程
图3所示为自主研发的水平单调加载试验系统,采用位移控制式加载。与荷载控制方法相比,位移控制方法得出的荷载-位移曲线更为准确[15]。试验加载速率v为0.1、0.25、0.5、2 mm/s。为保证试验的可重复性和准确性,在试验开始前严格控制试验初始条件和试验流程一致,并且对每个工况进行平行试验,重复至少3次[16]。为保证砂土在每次试验时具有相同的密实度,在每次试验前对砂土表面以及沿竖直方向以下3倍基础高度范围内的砂土进行松动。砂土松动后将基础埋置到预定位置和高度,进行砂土回填,对基础侧壁周围的砂土进行震动密实,将基础周围砂面刮平,使砂面略高于基础顶面,以保证对砂土进行夯实后砂土表面与基础表面持平。
试验过程中采用击实锤及圆形铁片对基础周围砂土进行夯实,具体做法是:将圆铁片放置在贴近基础边缘,夯实锤提高到最大高度后自由落下,依靠惯性对砂土进行夯实,每次每个位置击实20次,每一个击实圆与之前一个击实圆面积重合1/3以保证砂土之间的充分密实,夯实结束后将砂面刮平。
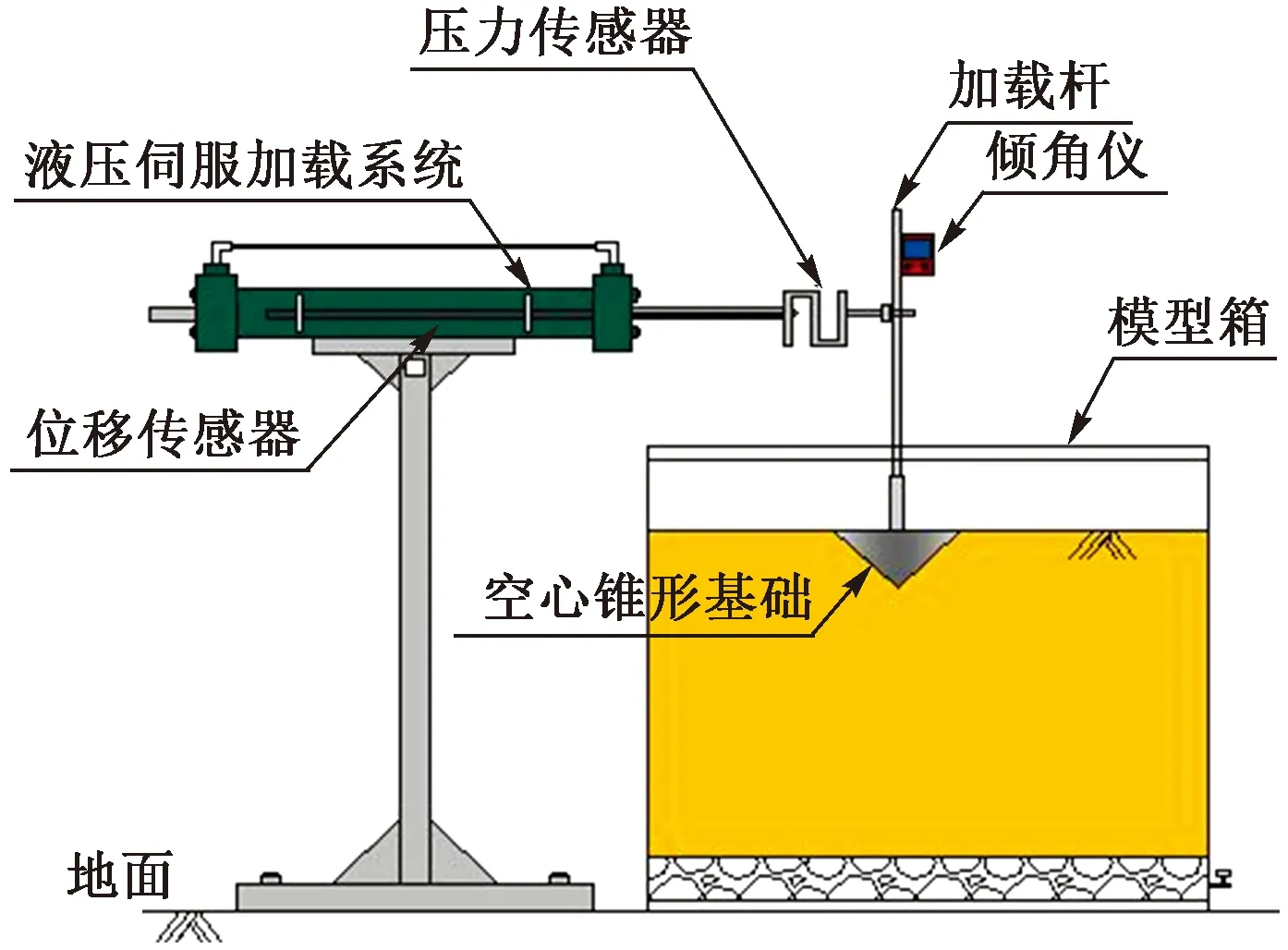
图3 模型试验装置Fig.3 Model test setup
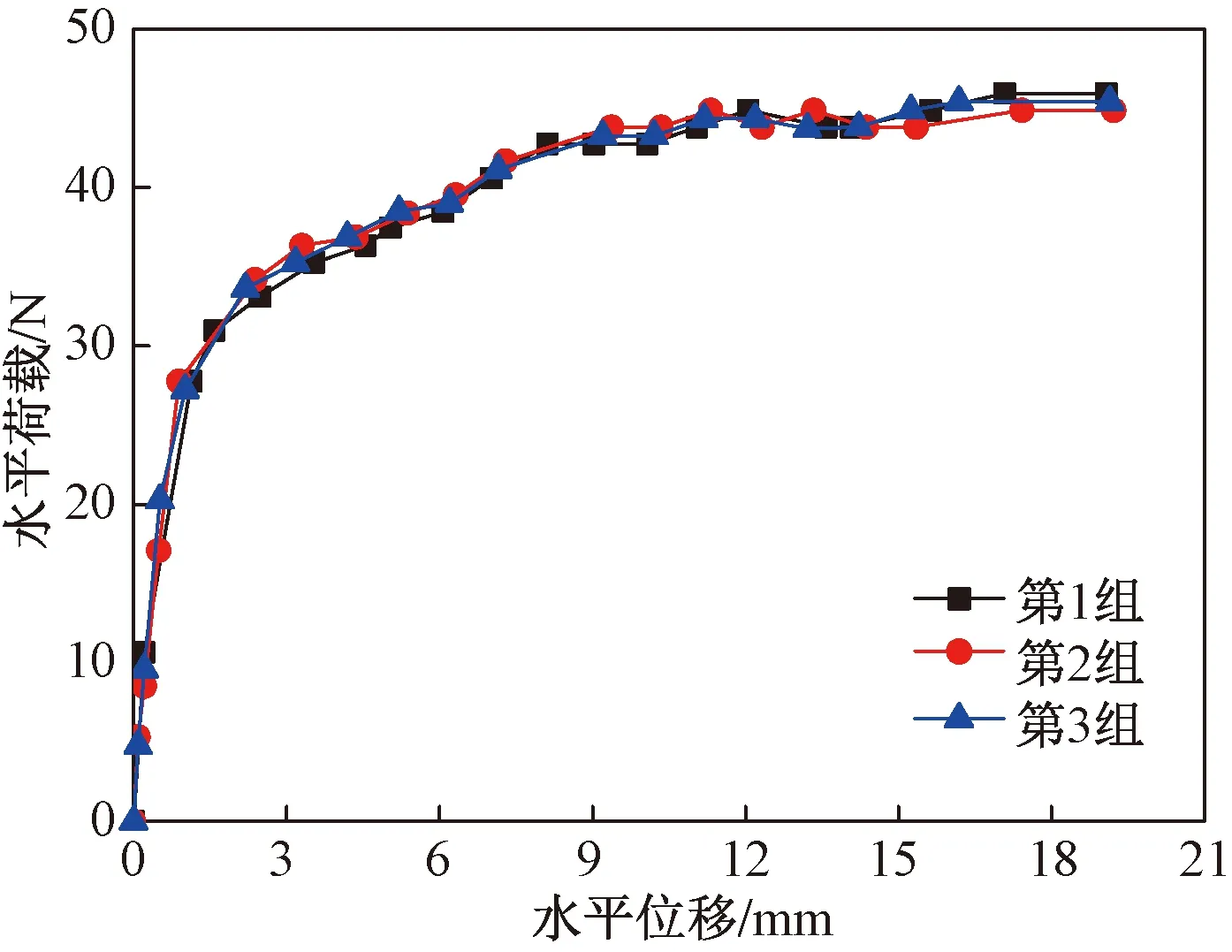
图4 荷载-位移关系Fig.4 Load-displacement relationship
2 锥形基础水平单调承载力影响因素分析
以锥形基础II-1为例,加载高度和加载速率分别为37.5 cm(对应的无量纲化加载高度h/D为1.25,其中h为实际加载高度,D为上顶板直径)和0.5 mm/s,进行3组重复平行试验,得到其荷载-位移关系,如图4所示。对比3组平行试验可知,荷载-位移关系曲线吻合较好,相对误差小于5%,认为每次试验条件一致。
由图4以及观察试验过程可知,加载过程可分为3个阶段:
第Ⅰ阶段,随着水平位移增加,基础受到的水平荷载呈线性增加,此时基础周围土体处于弹性变形阶段,加载点处位移较小。
第Ⅱ阶段,随着水平位移继续增加,基础受到的水平荷载持续增加,但增幅逐渐减小直至达到一定值,沿加载方向基础前侧土体出现变形。
第Ⅲ阶段,继续对基础施加恒定速率的位移,加载点位移持续增大但基础所受水平荷载基本保持不变,直至基础倾覆失稳。
研究表明,当基础荷载-位移曲线的斜率接近或者达到零时,表示基础荷载不再随位移增大而改变,此时对应的承载力为基础极限承载力,所对应的荷载为极限荷载[17]。取基础荷载-位移曲线中斜率接近零时对应的荷载为基础的水平极限荷载。分析试验数据得出,基础达到水平极限荷载时对应加载点水平位移为0.02倍的基础顶板直径。
2.1 加载高度对锥形基础水平承载力的影响
冯凌云等[16]研究发现加载高度是风电塔架基础水平承载力的影响因素之一。试验选用的加载高度h分别为22.5、30、37.5 cm(与其对应的无量纲化加载高度h/D为0.75、1、1.25),加载速率均为0.1 mm/s。
图5(a)和图5(b)分别为锥形基础II-1和II-3在不同加载高度下的荷载-位移关系曲线。从图5中可以看出,加载速率相同时,当加载高度由22.5 cm增加到37.5 cm时,基础极限水平承载力急剧下降,高度增加对水平极限承载力的减小作用非常明显。
表2和表3分别为锥形基础II-1、 II-3分别在不同加载高度下的水平极限承载力。对于基础II-1,加载高度分别为22.5 cm和30 cm时,水平极限承载力比加载高度为37.5 cm时的水平极限承载力分别增大了85.6%和35.7%。对于基础II-3,当加载高度为22.5 cm和30 cm时,水平极限承载力比加载高度为37.5 cm时的水平极限承载力分别增大了72.1%和33.8%。
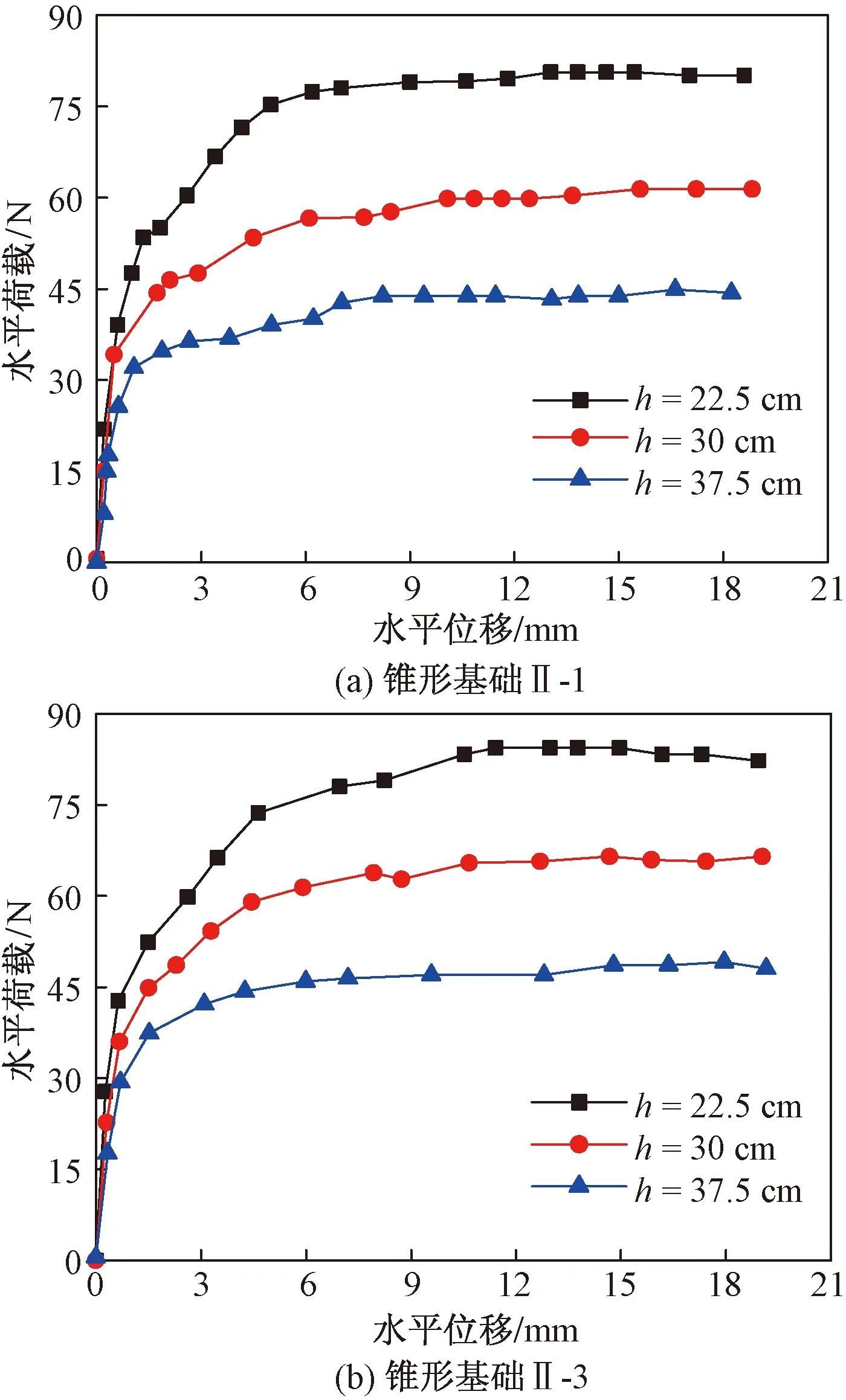
图5 不同加载高度下荷载-位移关系Fig.5 Load-displacement relationship under different loading heights
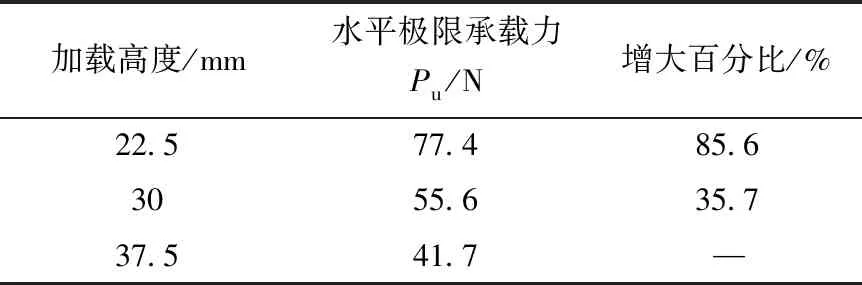
表2 不同加载高度下锥形基础II-1水平极限承载力Table 2 Ultimate bearing capacity of cone-shaped foundation under various loading eccentricities
图6所示为不同加载高度下锥形基础的水平极限承载力和基础顶板弯矩承载力与加载高度关系。基础顶板所受弯矩为基础水平承载力与加载高度的乘积。由图6可知,锥形基础的水平极限承载力与加载高度呈线性关系,并随着加载高度的增加而降低。但是达到水平极限承载力时基础顶板所受弯矩随加载高度的增加基本不变。

图6 不同加载高度下锥形基础水平极限承载力和弯矩承载力Fig.6 Ultimate bearing capacity and overturning moment of cone-shaped foundation under various loading eccentricities
2.2 加载速率对锥形基础水平承载力的影响
选用基础II-1~II-4,研究加载高度h=37.5 cm,加载速率v分别为0.1、0.25、0.5、2 mm/s时锥形基础的水平承载力,基础荷载-位移关系曲线如图7所示。可以看出,加载速率对水平承载力影响较小。其原因为模型地基中的砂土是干砂,试验过程中土体处于完全排水状态,所以加载速率对基础的水平承载力影响较小。

图7 不同加载速率下荷载-位移关系Fig.7 Load-displacement relationship under different loading rates
2.3 模型尺寸对锥形基础水平承载力的影响
选择锥形基础II-1~II-5,研究基础径高比和底板尺寸对水平承载力的影响。
选取径高比分别为5、6、5.5的锥形基础II-1、II-4、II-5,在加载高度h分别为22.5 cm和37.5 cm、加载速率均为0.1 mm/s时对基础荷载-位移关系进行分析,其荷载-位移关系曲线如图8所示。由图8可以看出,在加载前期位移较小时,3个基础的荷载-位移曲线几乎一致;随着荷载增加,3个基础的荷载均持续增大,但荷载增长速率不同。当达到水平极限荷载时,径高比为5.5的基础II-5水平极限承载力最大,径高比为5的基础II-1水平极限承载力最小。

图8 不同径高比基础荷载-位移曲线Fig.8 Load-displacement curves of foundation with different diameter-height ratio
表4和表5分别为不同加载高度下,锥形基础水平极限承载力及增大百分比。当加载高度分别为22.5 cm和37.5 cm时,径高比为6的锥形基础II-4水平极限承载力比径高比为5的锥形基础II-1水平极限承载力分别增加了30.7%和30.5%,径高比为5.5的锥形基础II-5水平极限承载力比径高比为5的锥形基础II-1水平极限承载力分别增加了46.8%和48.7%。可以看出,径高比对基础的水平极限承载力影响显著。

表4 不同径高比下锥形基础水平极限承载力(h=22.5 cm)Table 4 Ultimate horizontal bearing capacity under various diameter-height ratio(h=22.5 cm)

表5 不同径高比下锥形基础水平极限承载力(h=37.5 cm)Table 5 Ultimate horizontal bearing capacity under various diameter-height ratio(h=37.5 cm)
探讨基础底板尺寸对锥形基础水平极限承载力的影响,选取顶板直径相同,底板直径为0、50、85 mm(底板直径与顶板直径之比d/D分别为0、0.17、0.28)的锥形基础II-1~II-3,加载高度h=37.5 cm时基础的荷载-位移关系进行分析,荷载-位移曲线如图9所示。基础水平极限承载力及其增大百分比如表6所示。可知水平承载力随基础底板直径的增大而增大。在相同水平位移时,底板直径为85 mm(d/D=0.28)的基础II-3水平极限承载力最高,其次是基础II-2(d/D=0.17),基础II-1(d/D=0)的水平极限承载力最低。底板直径从0增加至50 mm和85 mm,即d/D从0增加到0.17和0.28时,锥形基础的水平承载力分别增加了4.6%和10.0%。由此可以得出,基础水平承载力与底板尺寸相关,且基础底板对锥形基础水平承载力起促进作用,随着底板直径增大,基础的水平极限承载力提高。同样,在相同水平荷载时,基础侧移量随底板尺寸增大而减小,即增大底板尺寸可控制基础水平侧移,有利于基础稳定。
图10所示为锥形基础II-3~II-5在加载高度和加载速率相同时,加载过程转角随水平位移的变化规律。由图中可以看出:在相同的水平荷载下,锥形基础II-3的转角最大,基础II-5转角最小;当基础发生相同转角约为1°时,3个锥形基础的水平荷载几乎不再增加,达到稳定,此时锥形基础II-5的水平荷载最大,锥形基础II-3的水平荷载最小。其原因为:在加载初期基础处于线性加载阶段,基础的水平位移较小但荷载增加显著,此时基础转角变化较小,基础的主要运动形式为平动加转动;当位移持续增加,基础转角变化增大,而基础水平承载力在持续增加,但增幅有所减小;加载后期基础破坏失稳,此时基础的运动形式以转动为主,表现为随着加载位移增加,基础的转角增加幅度明显增大,而基础水平承载力不再继续增大。
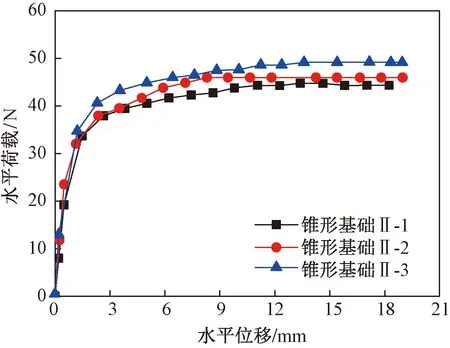
图9 不同底板尺寸下荷载-位移曲线Fig.9 Load-displacement curves under different floor sizes

表6 不同底板尺寸下锥形基础水平极限承载力Table 6 Ultimate horizontal bearing capacity under different diameter-height ratio

图10 基础转角与水平荷载关系Fig.10 Relationship between rotational angle of foundation and horizontal load
3 圆形基础和锥形基础水平承载力对比分析
为研究传统圆形基础和锥形基础水平承载力的不同,试验过程中分别对径高比和顶板直径相同的圆形基础和锥形基础,以及对相同质量但径高比不同的圆形基础和锥形基础水平单调承载力进行了对比。
图11所示为圆形基础和锥形基础单调水平加载的荷载-位移曲线。其中图11(a)所示为径高比和顶板直径相同的圆形基础I(底板与顶板直径之比d/D为1)和锥形基础II-1、II-2、II-3(底板直径分别为0、50、85 mm,对应的d/D分别为0、0.17、0.28)的荷载-位移曲线。由图中可以看出,在顶板直径相同时,圆形基础I的水平承载力比锥形基础II-1、II-2、II-3的水平极限承载力大。在线性加载阶段,加载点水平位移从0增加至1 mm,4条曲线吻合较好,基础水平承载力相差较小;随着位移的增加进入塑性变形阶段,基础水平承载力继续增大,但圆形基础的水平承载力的增加幅度较大;加载后期,圆形基础的水平承载力逐渐降低,而锥形基础的水平承载力持续缓慢提高,此时基础已经失稳破坏。另外,对于相同径高比和顶板直径的圆形基础和锥形基础,锥形基础底板的尺寸会对基础的承载力产生影响,底板尺寸较大的锥形基础(d/D为0.17~0.28)水平承载力相对较高,底板尺寸为0的锥形基础承载力低于圆形基础。
图11(b)所示为具有相同质量但径高比不同的圆形基础I和锥形基础II-4、II-5在加载高度和加载速度相同时水平荷载-位移变化关系曲线。在达到水平极限承载力时,锥形基础II-4的水平极限承载力是具有相同质量的圆形基础水平极限承载力的1.1倍,而锥形基础II-5的水平极限承载力为圆形基础水平极限承载力的1.2倍。这说明同等用钢量情况下,锥形基础的承载力优于圆形基础。
比较图11(a)和图11(b)可以看出,随着水平位移的持续增加,圆形基础的水平承载力有所降低,而锥形基础的水平承载力有所增加,增幅为7%~14%。其原因为在锥形基础达到水平极限承载力后随着水平位移的继续增加,锥形基础边缘的“尖端”嵌入密实的土中,此时基础侧壁对土体调动作用面积增大,导致基础的水平承载力继续增加。而圆形基础主要靠自重抵抗水平作用力,当基础作用点受水平力作用转角发生较大变化后,基础此时主要的运动形式为转动,土体发生明显的隆起变形,圆形基础水平承载力降低。
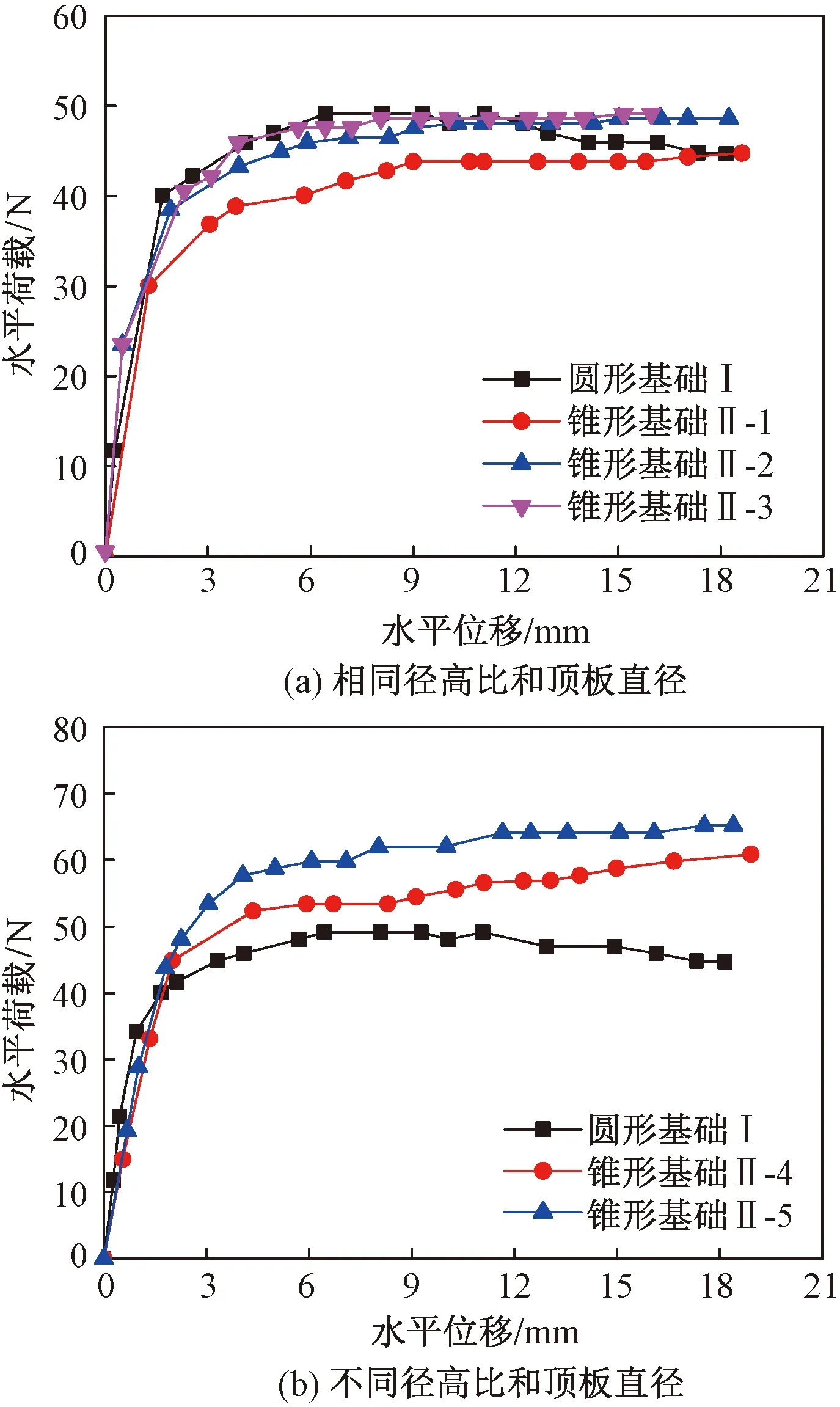
图11 圆形基础和锥形基础荷载-位移关系Fig.11 Load-displacement relationship of circular foundation and cone-shaped foundation
4 结论
通过开展砂土中位移控制式水平单调加载模型试验,分别对锥形基础水平承载力的影响因素及转动点变化规律进行了分析,得出结论如下。
(1)与圆形基础相比,锥形基础能有效控制基础的位移。锥形基础的水平极限承载力随着加载高度的增加而降低。加载速率对基础水平承载力的影响不明显。
(2)基础水平极限承载力随径高比的增大先增加后减小,随底板尺寸增加而增大。径高比为5.5的锥形基础水平承载力最高;径高比相同时,不同底板尺寸的锥形基础中,底板直径最大的锥形基础(底板直径85 mm)水平承载力最高,底板直径为0的锥形基础水平承载力最低。增大基础底板尺寸能有效控制水平侧移。
(3)基础转角在加载初期变化较小,基础主要运动方式为平动;加载后期基础转角变化幅度明显增大,基础水平承载力持续增加但增幅减小,直至保持不变,这一过程中基础的主要运动方式为转动。
(4)相同径高比和顶板直径的锥形基础和圆形基,底板直径为0的锥形基础承载力低于圆形基础,底板直径为50、85 mm(d/D为0.17、0.28)的锥形基础承载力较高。相同质量的锥形基础和圆形基础,锥形基础的水平承载力高于圆形基础。
