异常高压气藏水平井气水两相产能模型建立及应用
2020-07-14耿惠丽邓清源周光亮
罗 静,耿惠丽,邓 波,曹 建,邓清源,周光亮
(1.中国石油西南油气田公司,四川 江油 621741;2.中国石油天然气股份有限公司,北京 100007)
0 引 言
异常高压气藏属于非常规气藏,具有地质条件复杂、开发潜力巨大、开发难度较大的特性[1-5]。目前采用等值渗流阻力法[6]、电模拟[7]、复变函数理论[8]、叠加原理[9-10]等方法进行水平井产能预测,但大多研究是在常规温度压力下进行,高压气藏的水平井产能模型研究较少[11-15]。同时,部分学者针对异常高压气藏的渗流机理及产能进行了研究[16-19],但都未考虑近、远井地带渗流差异及启动压力影响。
通过引入茹科夫斯基变换,将复杂水平井立体渗流问题转化为简单渗流问题,并分别定义近井带、远井带气水两相拟压力,考虑出水与近井地带非达西效应的影响,将推导所得公式相耦合,建立气水运动方程,并定义气水广义拟压力,同时考虑启动压力梯度、气体滑脱效应、储层应力敏感等因素对气井产能的影响,使模型更贴近生产实际,为异常高压气藏水平井气水两相产能预测提供了新的解决思路。
1 模型假设
采用Josey经典分解方法将1个复杂水平井立体渗流问题分解为2个简单的平面径向渗流问题,即在垂直方向的径向流动及在水平方向的椭圆径向流动,而水平方向的流动通过保角变换转化为拟径向流动。
针对该异常高压气藏的产能模型提出如下假设:①初始状态下,气藏中的地层压力均为原始地层压力pi;②均质储层,上下边界封闭且等厚;③流体遵循非达西渗流规律,考虑表皮效应的影响,忽略毛管力和重力;④气井水平段长度为L,且位于储层中部;⑤水平井井筒内无限导流,水平气井的生产制度为定井底流压方式生产。
2 数学模型
2.1 近井地带水平井产能模型
近井地带的垂直平面径向流动是带状区域内的椭圆渗流问题,引入茹科夫斯基变换,采用保角变换函数将椭圆渗流转换为圆形渗流,将带状区域转换为单位圆形区域:
(1)
式中:h为气层厚度,m;z为Z坐标下的映射点;ξ为ξ坐标下的映射点。
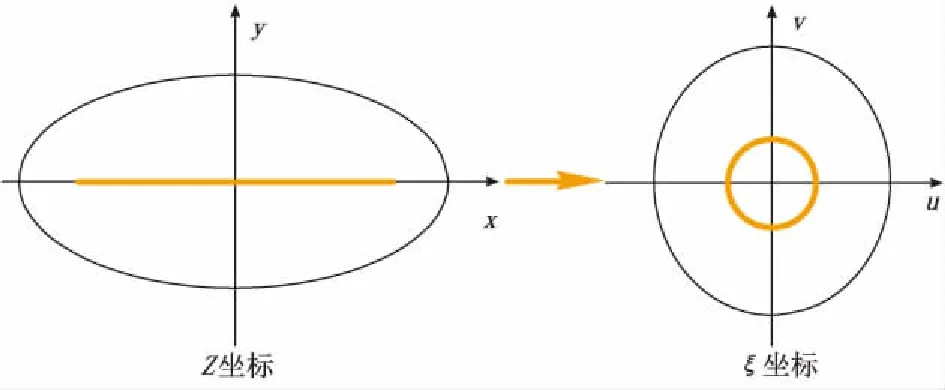
茹科夫斯基变换后,Z坐标下的带状区域(-0.5h 将Z坐标下的井筒半径rw转换为ξ坐标下的半径Rw,则气相与水相启动压力梯度为: 图1 垂直平面进行保角变换 (2) (3) 将式(2)、(3)带入气水两相运动方程,得: (4) 式中:p为径向上任一点压力,MPa;qg为地下产气量,m3/d;ρg为气体密度,kg/m3;βg为紊流系数;K为气藏测试渗透率,mD;Krw为水相相对渗透率,%;r为任一点的径向距离,m;μg为气相黏度,mPa·s;L为水平段长度,m。 (5) 式中:qw为地下产水量,m3/d;μw为水相黏度,mPa·s。 定义水气质量比为: (6) 式中:Rwg为水气质量比;mw为产水质量,kg;mg为产气质量,kg;qwsc为地面标准状况下产水量,m3/d;qgsc为地面标准状况下产气量,m3/d;ρw水的地下密度,kg/m3;ρwsc为地面标准状况下水的密度,kg/m3;ρgsc为地面标准状况下气的密度,kg/m3。 由式(5)、(6),结合气水两相渗流方程可得: (7) 式中:Krg为气相相对渗透率,%。 结合Klinkenberg考虑滑脱效应的测试渗透率计算公式与法夸尔绝对渗透率公式,将气水启动压力梯度定义为: (8) 式中:λwg为气水启动压力梯度,MPa/m。 定义气水两相广义拟压力为: (9) 式中:φ(p)为气水两相广义拟压力,MPa2/(mPa·s);α为应力敏感指数,MPa-1;pi为原始地层压力,MPa;δ为滑脱因子,MPa。 将βg=2.417×106/Ki1.5带入式(7)进行变量分离,并将式(9)代入进行积分,考虑表皮因子及紊流效应的影响,得到拟压力-压力函数表达式: (10) 式中:φ(pp)、φ(pwf)分别为近井地带驱动抉压力,井底流动拟压力,MPa2/(mPa·s);pi为原始地层压力,MPa;S为表皮系数;pp为近井地带驱动压力,MPa;Ki为原始渗透率,mD;pwf为井底流压,MPa。 (11) 式中:m(p)为拟压力,MPa2/(mPa·s)。 通过引入压力-半径函数表达式将式(10)简化为拟压力-半径函数表达式。在垂直平面的径向流动中,压力分布表达式为: (12) 将式(12)两边同时微分,得到r的表达式,并将其代入式(11),利用换元积分法可得: (13) 将式(13)带入式(10)则可得到近井地带产能公式: (14) 远井地带的水平面径向流动是椭圆渗流问题,引入茹科夫斯基变换,采用保角变换函数将椭圆渗流转换为圆形渗流,图2为水平平面进行保角变换结果,转换后的等效油井半径为1。 茹柯夫斯基变换后,远井地带水相、气相启动压力梯度变为: (15) (16) 考虑启动压力梯度,气水两相运动方程变为: (17) (18) 引入应力敏感指数与气体滑脱因子,将上式改为SI矿场单位制,结合定义的水气质量比,式(17)与式(18)经过变形可得: (19) 图2 水平平面进行保角变换结果 结合肯林肯伯格考虑滑脱效应的测试渗透率计算公式与应力敏感下的法夸尔绝对渗透率公式,将远井地带下的气水启动压力梯度定义为: (20) 将式(20)代入式(19),可推导得到: (21) 定义远井地带气水两相广义拟压力为: (22) 将远井地带气水两相广义拟压力函数φ(p)代入式(21),并对式(21)分离变量积分,得到远井地带产能公式。 (23) T1井为西南油气田九龙山气田茅口组气藏的一口水平井,原始地层压力为51 MPa,原始含水饱和度为0.345,储层厚度为37.8 m,水平井段长度为500 m,井筒半径为0.097 m,气藏供给半径为600 m,原始渗透率为1.89 mD,当前井底流压为32.45 MPa,气体相对密度为0.58,滑脱因子为0.5 MPa,应力敏感指数为0.01MPa-1。 储层岩石的气水相渗曲线通过岩心相渗实验获得,气水两相广义拟压力通过所得相渗曲线进行计算。由推导模型计算得到地层原始条件下该井的无阻流量为14.23×104m3/d,实际试气得无阻流量为13.70×104m3/d。表1为测井解释实测值与模型计算值的对比,由表1可知,井底压力越大,日产量越小,模型计算产量与实际产量的值越接近,贴合度越高,其相对误差为3.19%。 表1 试井解释实测值与模型计算值对比 3.2.1 水平井段长度对产能的影响 保持其他参数恒定,绘制出水平井段长度分别为300、400、500、600 m的异常高压气藏气井IPR曲线(图3)。由图3可知,水平井段越长,其对应的IPR曲线在坐标轴中越靠右,其无阻流量越大。 水平井段长度影响水平井产量,随着水平井段增长,井筒与气层的接触面积增加,水平井段的控制储量增加,对应的无阻流量增大,但其无阻流量的增加幅度减小。因此,需要结合经济评价,确定最佳水平井段长度,以获得最合理产量。 3.2.2 气体滑脱因子对产量的影响 保持其他参数恒定,绘制出气体滑脱因子分别为0.0、0.5、1.5、2.0 MPa的IPR曲线(图4)。由图4可知,气体滑脱因子越大,其IPR曲线在坐标轴中越靠右,无阻流量越大,但增大幅度较小,气井流入动态受滑脱因子的影响较小,且在井底流压较高、生产压差较低的情况下,可以忽略其对气井生产的影响。 图4 不同滑脱因子下的IPR曲线 Fig.4IPRcurves of different slip factors 3.2.3 应力敏感对产能的影响 保持其他参数恒定,绘制出应力敏感指数分别为0.000、0.005、0.010、0.015 MPa-1的异常高压气藏气井IPR曲线(图5)。由图5可知,储层的应力敏感指数越大,其对应的IPR曲线在坐标轴中越靠左,其无阻流量越小,且在井底流压越低时,储层应力敏感效应对水平井产量的影响越明显。 图5 不同应力敏感因子下的IPR曲线 (1) 通过引入茹科夫斯基变换,将1个复杂水平井立体渗流问题分解为2个简单平面径向渗流问题,并分别定义近井带、远井带气水两相广义拟压力,得到近井带、远井带的水平井产能公式,将推导所得公式相耦合,得到异常高压气藏水平井气水两相产能模型,为异常高压气藏产水水平井产能预测提供了一种新方法。 (2) 通过实例计算与水平井产能因素分析对比,推导模型的计算结果与现场试气得到的无阻流量相对误差小,模型可靠性高。在其他参数恒定情况下,水平井段长度增加,水平井的无阻流量减小;应力敏感因子增大,水平井的无阻流量也随之减小;异常高压气藏中气体滑脱因子对水平井产能影响较小。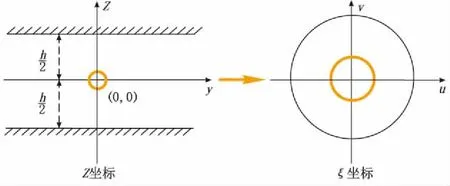
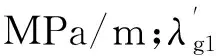

2.2 远井地带水平井产能模型
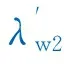



3 实例计算与影响因素分析
3.1 实例计算

3.2 影响因素分析


4 结 论
