多层级模糊联盟结构合作对策方法及其性质
2020-07-13杨靛青李院红俞裕兰
杨靛青,李院红,俞裕兰
(1.福州大学 经济与管理学院, 福建 福州 350002; 2.福建商学院, 福建 福州 350002)
0 引言
多层级联盟结构合作对策就是一种考虑局中人间存在限制联盟合作结构的合作对策。OWEN[1]提出两层联盟结构(简称联盟结构)合作对策,在Owen联盟结构思想的影响下,联盟结构合作对策的夏普利值(也称Owen值)[1]、班兹哈夫值[2]、τ值[3]和核心[4]等陆续被提出。WINTER[5]提出公理化多层级联盟结构合作对策夏普利值进而证明其满足的公理化性质。在此基础上,ALVAREZ-MOZOS等[6]将经典合作对策班兹哈夫值扩展到多层级联盟结构合作对策上,并将其和文献[5]提出的多层级结构夏普利值进行了公理化性质的比较分析。杨靛青等[7]构造了多层级联盟结构合作对策τ值,给出了该值的简便计算方法并讨论了其满足的公理化性质。TEJACA等[8]将多层级联盟结构和图状结构相结合,构造多层级图联盟结构合作对策。在现实管理中,由于客观原因限制,局中人可能以一定参与程度组成多层级联盟结构后参加大联盟合作,这种合作对策被称为多层级模糊联盟结构合作对策。孟凡永等[9]定义了基于Choquet积分的模糊合作对策班兹哈夫值并对其公理化性质进行证明和讨论。MENG等[10]进一步提出模糊联盟结构合作对策对称班兹哈夫值,证明该解的存在性和唯一性。杨靛青等[11]构造了基于Choquet积分的多层级模糊联盟结构合作对策τ值并对其公理化性质进行证明分析。笔者结合模糊集概念和多层级联盟结构思想,定义了班兹哈夫值,研究此类对策班兹哈夫值满足可加性、联盟内对称性、哑元性及联盟外无关性等性质,并进一步证明其唯一性。最后,通过算例比较分析多层级模糊联盟结构合作对策值班兹哈夫值和夏普利值的异同特性。
1 多层级模糊联盟结构合作对策
合作对策可表示为一个序对
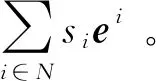
定义1对于
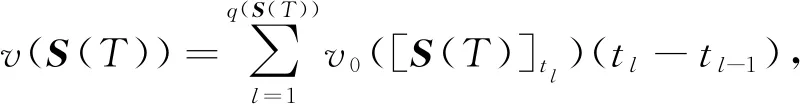
(1)
其中[S(T)]t={i|si≥t,i∈T},其中t∈[0,1];对于任意S(T),规定t0=0,称v是关于v0基于Choquet积分的模糊合作对策,记Gc(N)为基于Choquet积分的模糊合作对策的集合。
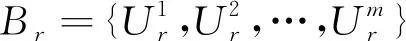
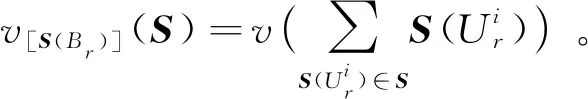
2 多层级模糊联盟结构合作对策班兹哈夫值及性质
2.1 多层级模糊联盟结构合作对策班兹哈夫值的定义
设
V(S(T),i)=v(S(T))-v(S(Ti)),
它表示局中人i在模糊联盟S(T)中的期望支付。根据定义1和式(1),有:
定义2给定一个多层级模糊联盟结构
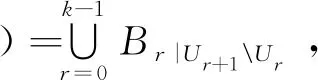
其中Uk=N。记P(i,B)集合中单元数为pi,则可记集合P(i,B)={T1,T2,…,Tpi}。
定义3设

(2)
其中Pi={1,2,…,pi},Q=∪r∈RTr,则称H(S,v,B)为多层级模糊联盟结构合作对策班兹哈夫值。
定理1设

(3)
其中H(v0[S]tl,B)是多层级联盟结构合作对策班兹哈夫值,对每个局中人i∈N,满足:
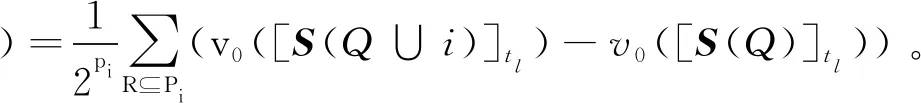
证明对于任意局中人i∈N,有:
其中Pi={1,2,…,pi}和Q=∪r∈RTr。根据定义3,有:

因此,有:

证毕。
2.2 多层级模糊联盟结构合作对策班兹哈夫值的性质
定理2多层级模糊联盟结构合作对策班兹夫值满足以下性质:
① 联盟单元对称性。对于任意i,j∈U∈B1,T⊆Ni,j,若v(S(T∪i))=v(S(T∪j)),则Hi(S,v,B)=Hj(S,v,B);
② 哑元性。若i∈N满足对于任意T⊆Ni有v(S(T∪i))=v(S(T))+v(S(i)),则Hi(S,v,B)=v(S(i));
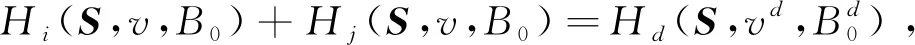
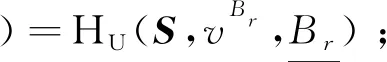
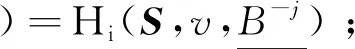
⑥ 等价边际贡献性。给定S∈L(N)且v,w∈Gc(N),若存在i∈N满足对于任意T⊆Ni有v(S(T∪i))-v(S(T))=w(S(T∪i))-w(S(T)),则Hi(S,v,B)=Hi(S,w,B);
⑦ 可加性。给定S∈L(N)且v,w∈Gc(N),则H(S,v+w,B)=H(S,v,B)+H(S,w,B)。
证明性质①、②、④和⑦容易证明满足条件,下面重点证明性质③、⑤和⑥。
设

若存在i,j∈N满足{i,j}⊆U∈B1,则:
P(i,B)={T1,T2,…,Tl,…,Tpi},
其中j∈Tl且l∈{1,2,…,pk},和:
其中Tl′=Tlj且Tpi+1={j},进一步有:
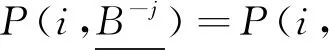
根据式(2),有:
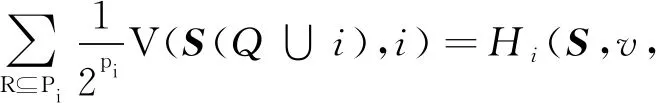
v,w∈Gc(N),存在i∈N满足对于任意T⊆Ni有v(S(T∪i))-v(S(T))=w(S(T∪i))-w(S(T)),则:


2.3 多层级模糊联盟结构合作对策班兹哈夫值的唯一性
定理3在多层级模糊联盟结构合作对策中,班兹夫值是唯一满足联盟单元对称性、哑元性、2-有效性、多层单体联盟性质、个体分离无关性、等价边际贡献性和可加性的对策解。
证明定理2已证明班兹哈夫值满足这七种性质,现在只要证明该对策解是满足这七种性质的唯一解。

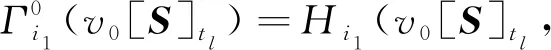
现在假设联盟层级k=n-1时,Γi1(S,v,B)=Hi1(S,v,B)。证明当k=n时,Γi1(S,v,B)=Hi1(S,v,B)成立。设i1∈U∈B1,若|U|=u=1,即U={i1}。由于Γi1满足多层单体联盟性质,
Γi1(S,v,B)=Γ[U](v[S(B1)]),
同时,Hi1也满足多层单体联盟性质,则:
Hi1(S,v,B)=H[U](v[S(B1)]),
由于联盟层级k=n-1时,Γi1(S,v,B)=Hi1(S,v,B),即:
Γ[U](v[S(B1)])=H[U](v[S(B1)]),
因此,可得:
Γi1(S,v,B)=Hi1(S,v,B)。
进一步假设当|U|≤u时,Γi1(S,v,B)=Hi1(S,v,B)成立,证明当|U|=u+1时,等式成立。设i1∈U∈B1且j∈Ui。由于Γi1满足个体分离无关性,则:
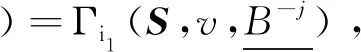
同时,Hi1满足个体分离无关性,则:
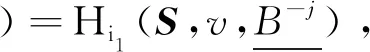
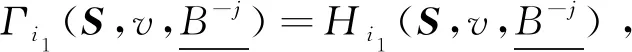
Γi1(S,v,B)=Hi1(S,v,B),
成立。证毕。
3 算例分析
假设局中人集合N={1,2,3,4},合作对策

表1 合作对策

下面给出一组随机形成模糊联盟,利用式(1),计算不同模糊联盟形式下的支付,根据式(2)和文献[5],分别计算模糊多层级联盟结构合作对策班兹哈夫值和夏普利值,如表2所示。

表2 模糊多层级联盟结构合作对策班兹哈夫值和夏普利值
从表2看,可以验证班兹哈夫值和夏普利值都满足可加性、哑元性、联盟单元对称性、多层单体联盟性质、联盟外无关性,分配策略具有一定的公平合理性。通过比较分析,多层级模糊联盟结构合作对策班兹哈夫值和夏普利值的特性上有以下三点不同。
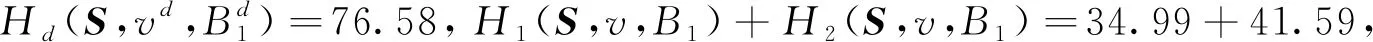


表3 模糊多层级联盟结构合作对策班兹哈夫值和夏普利值比较
4 结语
本文定义了多层级模糊联盟结构合作对策班兹哈夫值, 讨论其满足可加性、联盟单元对称性和联盟外无关性等性质,该值是合作对策班兹哈夫值的一般形式,但该班兹哈夫值的联盟结构相对固定, 下一步将重点研究不同联盟结构对班兹哈夫值的影响.
