二值纵向数据的经验似然分析

尹长明,靳永涛,王亚东

(广西大学 数学与信息科学学院, 广西 南宁 530004)

0 引言

二值数据是指响应变量的观测结果有两种情形，例如观测某人是否有心血管疾病，银行对某个客户是否贷款，学生考试是否及格等。纵向数据是对一个个体进行多次观测的数据，其中对一个个体多次观测的数据之间是相关的(相关系数不知道)，而不同个体观测的数据之间是独立的。LIANG等[1]提出的广义估计方程(generalized estimated equation, GEE)方法是对纵向数据进行分析的重要工具，研究文献很多[2-5]。广义估计方程的一个重要性质是即使工作相关系数假设错误，得到的估计仍然是相合的和渐近正态的。若工作相关系数等于真实相关系数，得到的估计渐近方差最小。经验似然也是一种重要的数据分析方法，有很多突出的优点，如用经验似然构造置信区间除有域保持性，变换不变性及置信域的性质由数据自行决定等诸多优点外，还有Bartlett纠偏性及无须构造轴统计量等优点[6-9]。QIN等[6]用经验似然方法研究了独立同分布的广义估计方程，LI等[7]用经验似然方法研究了广义线性模型下的广义估计方程，但条件不易验证，其结果也不理想。

下面将在易验证和比较弱的条件下证明二值纵向数据下经验似然估计的渐近性质。

设对第i个个体的第j次观测后同时得到一个二值响应变量Yij和一个p×1维协变量Xij(i=1,…,n,j=1,…mi)。设不同个体之间观测的数据是独立的，同一个个体mi次观测的数据是相关的。XT表示X的转置,记Yi=(Yi1,…,Yimi)T,Xi=(Xi1,…,Ximi)T。假设Yij期望为：

(1)

达到最小的β，其中t(β)满足约束条件：

本文约定C,C1,C2,…表示与n无关的正常数，在不同的地方表达的值可以不一样。

对于二值纵向数据的经验似然估计简介可参考文献[9]。为了得到其渐近性质，先作如下假定：

① 存在正常数C, 使‖Xij‖≤C,1≤i≤n,1≤j≤mi，即Xij一致有界。

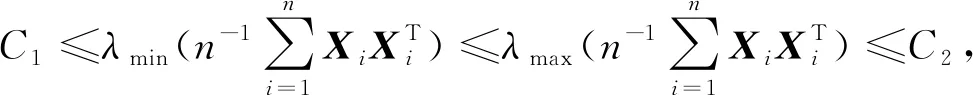
③ 存在C>0使得λminRi≥C,λminRo≥C, 其中Ro表示真实相关阵。

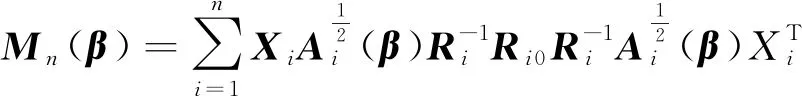
定理2若条件①～③及假设H0:β=β0成立，则经验似然比统计量为：

1 定理的证明

在给出上面主要结果的证明之前，需要如下引理：

(2)

C1I≤Ai(β0)≤C2I;C1I≤Ri≤C2I;

C1I≤Ri0≤C2I;C1Fn≤Ri≤C2Fn。

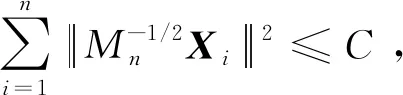
由上面结果易知：

再由Lindeberg中心极限定理即得式(2)成立，命题得证。

引理2在满足条件①～③下，有[7]：

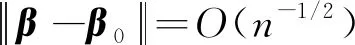
(3)

则有：

t(β)=Op(n-1/2)。

证明由式(3)知：

上式令t=t(β)，变形得：

(4)

用文献[4]给出的方法可以证明，以概率有：

再由微分中值定理、引理1和引理2可得：

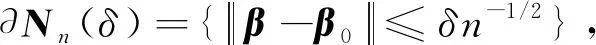
通过矩阵运算得：

再由约束条件(2)及引理2和引理3有：

对式(1)运用泰勒展式,得：

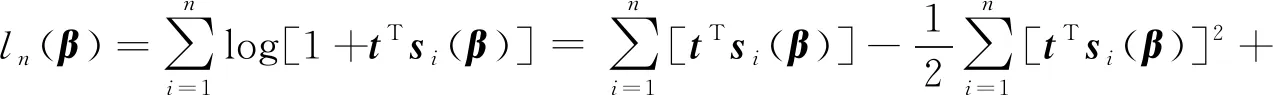
由引理2和引理3可知：

另一方面运用Cauchy-Schwarz不等式，则有：

因而：

由微分中值定理对上式在β0点展开有：

和存在正常数C1,C2使得：

所以，当β∈∂Nn(δ)时,有：

再由Cauchy-Schwarz不等式：

所以当δ充分大时，在β∈∂Nn(δ)有：

ln(β)≥ln(β0),

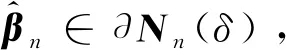
即：

其中：

定理2的证明类似文献[6]中定理2的证明，在此省略。

2 统计模拟

模型P(Yij=1|Xij)=e0.3Xij/[1+e0.3Xij],Xij服从独立的标准正态分布，详细二值数据模拟生成可参考文献[10]，工作相关阵Ri定义如下：

运用R语言运行广义估计方程GEE和经验似然EL方法的结果见表1和表2。

表1 100样本下GEE和EL方法的比较

表2 10 000样本下GEE和EL方法的比较

从数值模拟结果可看出,EL估计参数拟合度在大样本情况下比GEE估计结果更为理想。