Massive MIMO系统的信道建模及其性能研究
2020-07-13仇桐同周杰陈珍岳壮
仇桐同,周杰*,2,陈珍,岳壮
(1.南京信息工程大学 电子与信息工程学院, 江苏 南京 210044;2.日本国立新泻大学 工学部电气电子工学科, 日本 新泻 950-2181)
0 引言
目前,多输入多输出(multiple input multiple output, MIMO)技术已经在4G通信中获得了充分研究与实现,各项技术实现比较成熟。大规模MIMO系统被认为是5G蜂窝网络的候选技术,其可以实现高数据速率和高能量效率,从而引起了广泛的研究兴趣[1-2]。
现在关于大规模MIMO系统的研究还有很多。文献[3]针对阴影衰落进行了建模,研究了大规模MIMO的阴影衰落对信道容量的影响。文献[4]研究了通过大规模MIMO系统来提高通信系统吞吐量和系统性能。文献[5]针对大规模MIMO系统研究了误码率和信道参数的估计,比较了传统MIMO系统和大规模MIMO系统的性能。目前对于信道模型的研究还比较少,信道模型不仅能反映信号的传播特性,而且在进行测量之后可以对通信系统的性能进行评估,因此建立合理有效的信道模型就非常重要[6]。当下多数对于大规模MIMO系统的研究[7-9]都是基于信道独立性的假设之上,且采用独立同分布的Rayleigh衰落信道。大规模MIMO系统拥有配备了大量天线的基站,可同时服务于区域中的各个接收用户,文献[10]指出当基站处的天线数量越来越多,在大规模MIMO系统中,当发射端与接收端的距离小于Rayleigh距离时,波阵面不为平面,不能满足PW条件,此时就应该将模拟近场效应的SW纳入考虑。
笔者提出了一种ULA型3D几何信道模型,该模型考虑了远场效应和近场效应两种传输场景。基于统计物理信道模型分析了AAoA和EAoA的关系,研究了参数对平均相关性和信道容量的影响。仿真实验结果表明近场效应有助于对天线进行去相关性,随着天线数量的增加,特定天线和系统天线的平均相关性都将在一定程度上降低, SW效应随着发射端和接收端的距离增加而减弱,其信道容量逐渐趋近于PW模拟的信道容量曲线,当距离足够远时,SW可以被看作PW。
1 大规模MIMO系统天线的信道模型
1.1 远场效应的信道模型

图1 远场效应的信道模型
图1是远场效应的信道模型,对于ULA大规模MIMO系统天线的传播场景,提出了如图1所示的使用PW模拟的3D 几何ULA型大规模MIMO系统传输场景。

(1)
波前到达天线A1和天线A2的传输距离差为P2S2,则对应的时间延迟差为:
P2S2/c=dcos(π/2-αn)cos(βn)/c。
(2)

图2 近场效应的信道模型
1.2 近场效应的信道模型
图2是近场效应的信道模型,当发射机和接收机之间的距离小于瑞利距离时,就要考虑使用SW来模拟近场效应,提出了使用SW模拟的3D几何ULA型大规模MIMO系统传输场景。
和图1相比,图2的波前是球面的。假设信号来自于信号源S,S′是信号源S在x-S1-y平面的投影。S′与x轴的距离是dy,S′与y轴的距离是dx。h是点S和点S′之间的距离。基于这些参数,可以分析得到信号源S和每个天线之间的精确距离:
(3)
根据图2中的几何关系,可以得到:
(4)
变换表达式为:
(5)
2 分析天线平均相关性和信道容量
2.1 PW模拟的大规模MIMO天线的平均相关性
如图1所示,天线A1和天线A2的信道脉冲响应分别表示为:
(6)
(7)
式中,An表示第n个天线路径的接收幅度,φn表示第n个天线路径的接收相位,λ是载波波长。在ULA型大规模MIMO系统中,所有的天线都是均匀间隔的,使用PW模拟的远场效应中,所有的信号都是平行的,因此天线Am的信道脉冲响应可以表示为:
(8)

(9)

(10)

(11)

(12)

(13)

(14)
天线的平均相关性受到了环境散射,即α和β分布的影响,α分布的特性可以用均匀分布,拉普拉斯分布等来表征。本文使用具有一定角度扩展(angle spread, AS)的均匀分布来表示α分布,可以表达为:
(15)
式中,Δα表示AS,α0表示α分布的均值。使用余弦概率密度函数[12]来表达β分布:
(16)
式中,βmax是β的最大值。
2.2 SW模拟的大规模MIMO天线的平均相关性
如图2所示,以天线A1为参考天线,不同天线的信道脉冲响应可以表示为:
(17)

(18)

(19)
(20)
(21)
2.3 大规模MIMO系统的信道容量
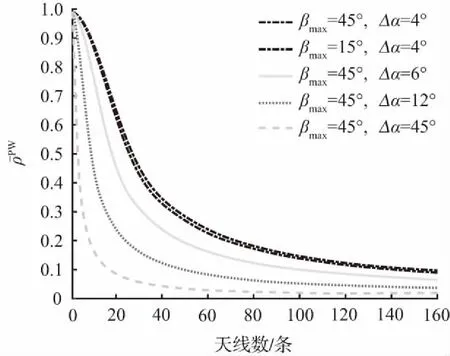
假设典型的均匀线性阵列(ULA)大规模MIMO系统的基站配备了M个天线,同时服务于K(K (22) 式中,det(.)表示行列式,I表示K×K单位矩阵,H表示K×M信道矩阵,HH表示H的共轭转置,ρ表示信噪比[16]。信道矩阵H用Kronecker模型建模[17],可以表示为: (23) 式中,Rr表示接收端的相关矩阵K×K数组,HIID表示K×M复杂高斯随机矩阵的独立同分布(independent and identically distributed, IID)信道,Rt表示发射端的相关矩阵M×M数组,对于大规模MIMO系统,本文仅考虑基站处的相关性,因为用户端的天线是不相关的,因此Rr=I。式中Rt的元素由公式(11)和公式(19)获得[18]。 MIMO多天线阵列通常是根据收发终端具体情况可设计为MIMO ULA,UCA和Y型阵列等模型,各种MIMO阵列均有其优缺点。本文基于大规模MIMO ULA多天线阵列,根据实际场景进行设置参数仿真,天线间隔d=λ/2,接收幅度归一化。本文重点分析了在不同Δα和最大βmax值下平均相关性之间的对比。 图3所示为Δα值的变化对使用PW模拟的天线A1的平均相关性的影响。βmax选取经典角度为45°,可以看出,特定天线的平均相关性受Δα的影响较大。由图3可知,Δα越大,则平均相关性越低。当天线数量较小时,较大的Δα相对于较小的Δα就显现出了增加Δα的优势。随着天线数量的增加,利用增加Δα的角度值来降低平均相关性的优势被减弱。 图4所示为βmax对使用PW模拟的天线A1的平均相关性的影响。Δα的值设置为4。由图4可知,在Δα不变的情况下,βmax对天线的平均相关性的影响很小,随着天线的增多,平均相关性的曲线几乎是重叠的,所以在大规模MOMO系统中,通过改变βmax来降低平均相关性的收益非常小。 图3 天线A1的平均相关性和天线数量的关系 Fig.3 Relationship between the average correlation of antennaA1and the number of antennas 图4βmax对PW模拟的天线A1的平均相关性的影响 Fig.4 Influence ofβmaxon the average correlation of antennaA1modeled by PW 图5所示为使用PW模拟的大规模MIMO系统天线的平均相关性与天线数量的关系。由图5可知,较大Δα的整个系统天线的平均相关性随着天线数量的增加,其降低平均相关性的优势被逐渐减弱。因此,和传统的MIMO系统相比,大规模MIMO系统并不需要富散射来降低平均相关性。结合图3~图5可以看出,当天线数量达到一定数量,特定天线或者整个系统天线的平均相关性随着天线的增加也不会有很大的幅度变化。 使用PW和SW模拟的大规模MIMO系统天线的平均相关性的对比见图6。βmax选取经典角度为45°,由图6可知,当dy较小时,使用SW模拟的大规模MIMO系统天线的平均相关性是低于PW的,表明了近场效应有助于天线的去相关性。随着dy的增大,SW的曲线逐渐靠近PW的曲线,表明随着发射端和接收端之间距离的增加,SW效应也随之减弱。 图5 天线数量对大规模MIMO系统天线的平均相关性的影响 Fig.5 Influence of antenna number on average correlation in massive MIMO systems 图6 PW和SW模拟系统天线的平均相关性的对比 Fig.6 Whole system antennas average correlation comparison modeled by PW and SW 图7 PW和SW模拟的系统信道容量的对比 使用PW和SW模拟的大规模MIMO系统天线的信道容量对比见图7。信噪比的值设置为15,K的值设为16,由图7可知,信道容量随着天线数量的增加而增加。结合图6和图7可以看出,较低的平均相关性对应较高的信道容量,并且随着dy的增大,SW模拟的信道容量曲线会越来越接近PW模拟的信道容量曲线。当天线数量很少时,4条曲线是重叠的,随着天线数量的增加,天线的尺寸结构变大,PW和SW模拟的信道容量之间的差异就显现出来。 针对大规模MIMO系统,提出了一种3D均匀线性阵列(ULA)的信道模型。信道建模方案具有简单和使用灵活的特点,针对不同的传输场景,推导了信道脉冲响应、空间相关函数、平均相关性。分别分析了远场效应,近场效应以及Δα、βmax、dy等对大规模MIMO信道容量的影响。研究结果表明,近场效应有助于天线的去相关性;随着天线数量的增加,特定天线和系统天线的平均相关性都会在一定程度上降低;当发射端和接收端的距离足够远时,随着SW效应的减弱,其信道容量逐渐趋近于PW模拟的信道容量曲线。该模型的信道参数设置符合理论和经验值,分析方法亦可用于进一步分析Y型阵列和UCA阵列,有效拓展了大规模MIMO信道模型的研究。3 实验仿真结果与分析




4 结语
