下部溶洞对抗滑桩的稳定性影响试验研究

2020-07-13杨鹏帅范秋雁韩进仕梁家珲

广西大学学报（自然科学版） 2020年3期

杨鹏帅，范秋雁*,2，韩进仕，梁家珲

(1.广西大学土木建筑工程学院，广西南宁 530004；2.广西大学资源环境与材料学院，广西南宁 530004；3.广东修邦代建工程管理有限公司，广东惠州 516000；4.山东大学岩土与结构工程研究中心，山东济南 250061)

0 引言

中国岩溶地区约占国土面积的1/3，近年来，岩溶地区工程建设中边(滑)坡治理工程越来越多，抗滑桩是治理边(滑)坡的有效措施。当桩周存在溶洞时，会对水平承载桩的承载性状产生影响。过去国内外对岩溶地区桩的稳定性研究主要集中在垂直承载桩方面，对岩溶地区水平承载桩研究甚少。FENG等[1]采用有限元数值模拟方法结合灰色系统理论分析了不同溶洞尺寸下桩的承载力变化规律。文献[2-4]采用有限元数值模拟方法,分析了荷载作用下，下部存在溶洞时，不同类型基础的承载能力，得出溶洞的存在对基础的稳定性影响显著。张永杰等[5]对垂直荷载作用下的溶洞顶板进行简化分析并探讨了不同空间形态溶洞顶板的破坏模式。赵明华等[6-7]运用理论分析方法研究岩溶区嵌岩桩桩端极限承载力的相关问题，提出理论模型及理论公式，并验证了其合理性。王倩[8]运用数值模拟方法分析了影响抗滑桩稳定性的影响因素，提出不同影响因素下桩到溶洞的安全距离公式。韩伟[9]基于室内模型试验研究了覆盖岩溶临空面对支护桩的稳定性影响，得出软弱结构面的存在显著影响支护桩的稳定性。梅博轩[10]运用有限元法结合工程实例，对岩溶地区基坑支护桩的稳定性进行了分析研究，得出溶洞位于主动侧、被动侧、正下方时不同因素对基坑稳定性的影响规律。江杰等[11]运用Midas-GTS有限元软件研究了不同位置、不同大小的溶洞对深基坑开挖的影响，得出溶洞所在位置不同，对基坑稳定性的影响程度也不同。以上研究没有对岩溶区抗滑桩存在下部溶洞时对抗滑桩稳定性进行室内模型试验研究，为此以抗滑桩下部存在溶洞为研究对象，构建室内相似物理模型，从裂纹起裂与扩展、桩水平位移及应变场等方面研究抗滑桩及桩周岩体破坏的影响规律及机理。

1 室内相似模型试验

1.1 模型尺寸及物理力学参数

原位岩体宽度30.0 m，高度21.0 m(其中嵌岩段岩体15.0 m，桩外露6.0 m)，厚度18.0 m。桩长10.0 m，桩径2.0 m，嵌岩4.0 m，假设桩采用连续咬合布置，整体模型可视为平面应变模型，连续咬合桩整体刚度远大于嵌固段石灰岩刚度，故采用钢板模拟连续咬合桩。溶洞截面简化为椭圆形，尺寸为长轴3.5 m，短轴2.0 m，溶洞顶部距离桩底2.0 m。为进行对比分析，建立无溶洞和下部有溶洞两个模型，模型几何相似常数设计为30，室内模型尺寸如图1，其中模型宽0.6 m。

岩溶区石灰岩的物理力学参数受岩石矿物构成、地下水等多种因素影响，变化范围较大，结合相关资料[12-14]，由于现场石灰岩整体性较好，在室内试验中，物理相似常数考虑为1.3。由相似理论可得应力与弹性模量的相似常数为39。原岩与模型主要参数取值如表1。

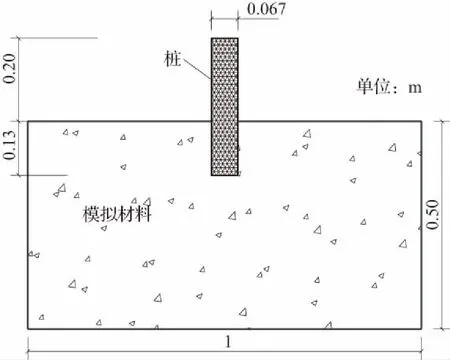
(a) 无溶洞模型

(b) 下部有溶洞模型

表1 主要物理参数

为了较好的模拟灰岩的物理力学性能，试验选定了水泥、石膏粉、河砂和重晶石粉作为相似材料的原材料，为防止石膏凝结过快，在搅拌过程中加入适量缓凝剂，模型浇筑完成之后，按规定对模型进行修整和养护。

1.2 加载测试系统

试验中，加载系统由分离式千斤顶(DYG50-500)和电动油泵构成，千斤顶行程0.5 m，油泵压力为60 MPa；量测系统由荷载传感器(SLZT-BT)和多功能数显仪(SL8016)组成；其中数显仪分辨率为0.01 kN；声发射探头尺寸直径×厚度为10 mm×12 mm，频率100～600 kHz，试验采用40 dB增益。相关设备如图2和图3。

图2 加载及量测系统

Fig.2 Loading and measuring system

图3 声发射及电阻应变仪

Fig.3 Acoustic emission and resistance strain gauge

1.3 模型加载

试验前在抗滑桩和千斤顶之间设置橡胶垫块，千斤顶与试验台固定，溶洞内左右两侧置入孔径位移计，分别量测长轴方向与短轴方向的孔径变形量。声发射围绕溶洞四周布置，并用硅脂与岩体粘贴。加载采用千斤顶分级加载形式，每级荷载加载稳定后进行相关数据的测量记录，加载速率为0.2 kN/min。实物布置如图 4和图5。

图4 无溶洞模型布置实物图

Fig.4 Physical picture of no-cave model

图5 下部有溶洞模型布置实物图

Fig.5 Physical picture of lower-part karst cave model

2 试验结果及分析

2.1 模型破坏分析

无溶洞模型和下部有溶洞模型在水平荷载作用下发生脆性破坏，发生脆性破坏之前，模型表面均无明显裂纹产生，随着模型加载，模型内部裂纹逐渐连通，当达到破坏荷载时，模型破坏瞬间完成，裂纹贯穿整个模型。破坏情况如图6和图7所示：

图6 无溶洞模型破坏情况

Fig.6 Destruction of no-cave model

图7 下部有溶洞模型破坏情况

Fig.7 Destruction of lower-part karst cave model

对比图6和图7可得到：

① 无溶洞模型和下部有溶洞模型分别在水平推力加载到11.25 kN时和6.52 kN时，模型破坏；存在溶洞的抗滑桩水平极限承载力(破坏荷载前一级荷载)约为无溶洞模型的0.57倍，溶洞的存在导致抗滑桩承载能力下降；

② 两个模型裂纹初始产生位置均靠近桩底主动区，无溶洞模型裂纹初始以沿水平方向夹角约60°角扩展，有溶洞模型下部裂纹初始以沿水平方向夹角80°角扩展，溶洞的存在增大了裂纹的扩展角度，下部有溶洞模型裂纹起裂位置向桩中心线偏移一定位置，裂纹扩展方向向被动区偏转并贯穿溶洞。

2.2 荷载—位移分析

为量测试验过程中抗滑桩、主动区、被动区的位移变化，分别在无溶洞模型和下部有溶洞模型的不同位置设置多个百分表，在试验初始阶段，模型内部初始微孔隙逐渐被压密，以及在施加荷载之后，模型整体的紧密程度进行调整，故在加载一定时间之后，百分表读数才发生变化。所得荷载—位移曲线如图8所示：

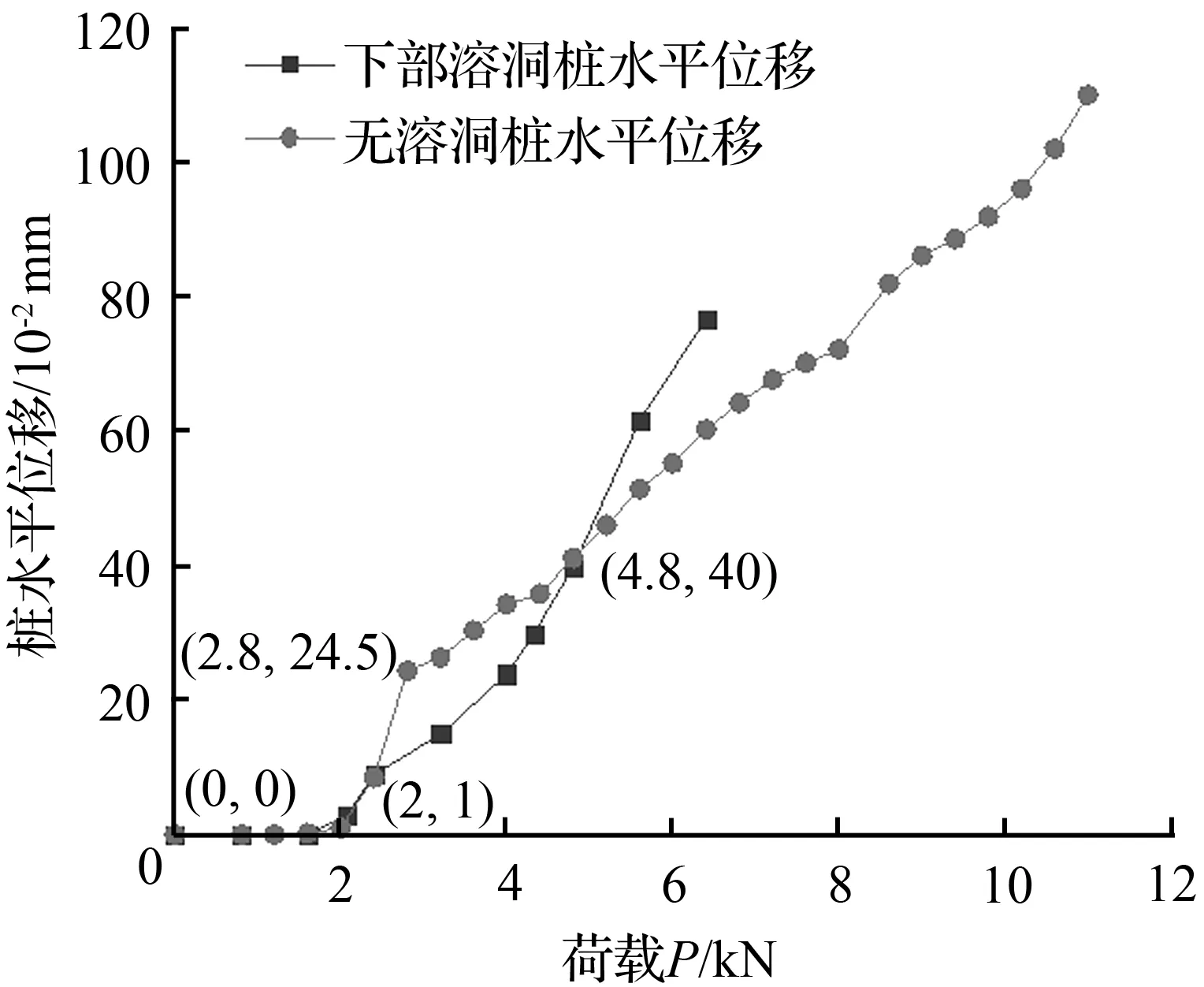
(a) 荷载—桩水平位移曲线

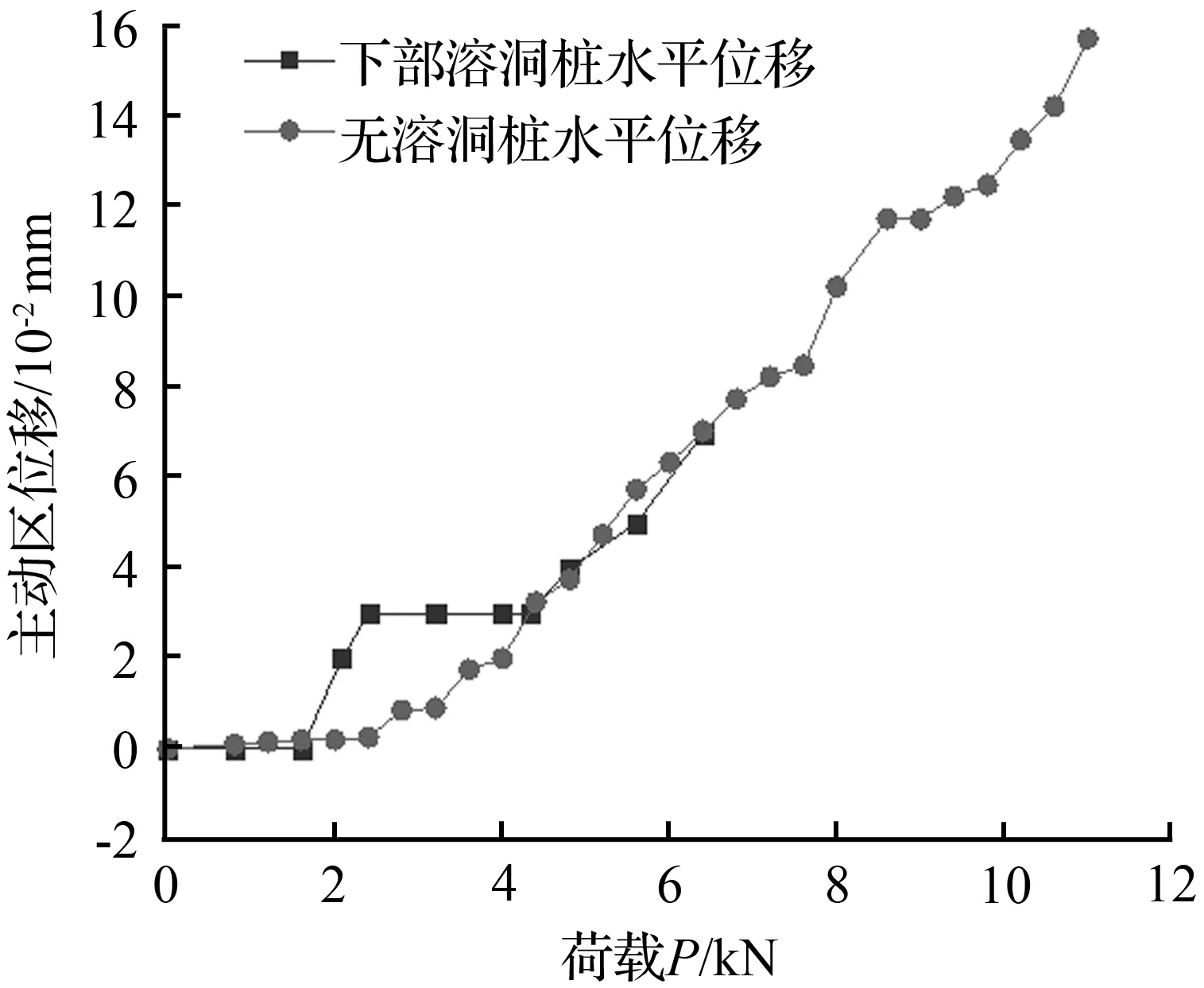
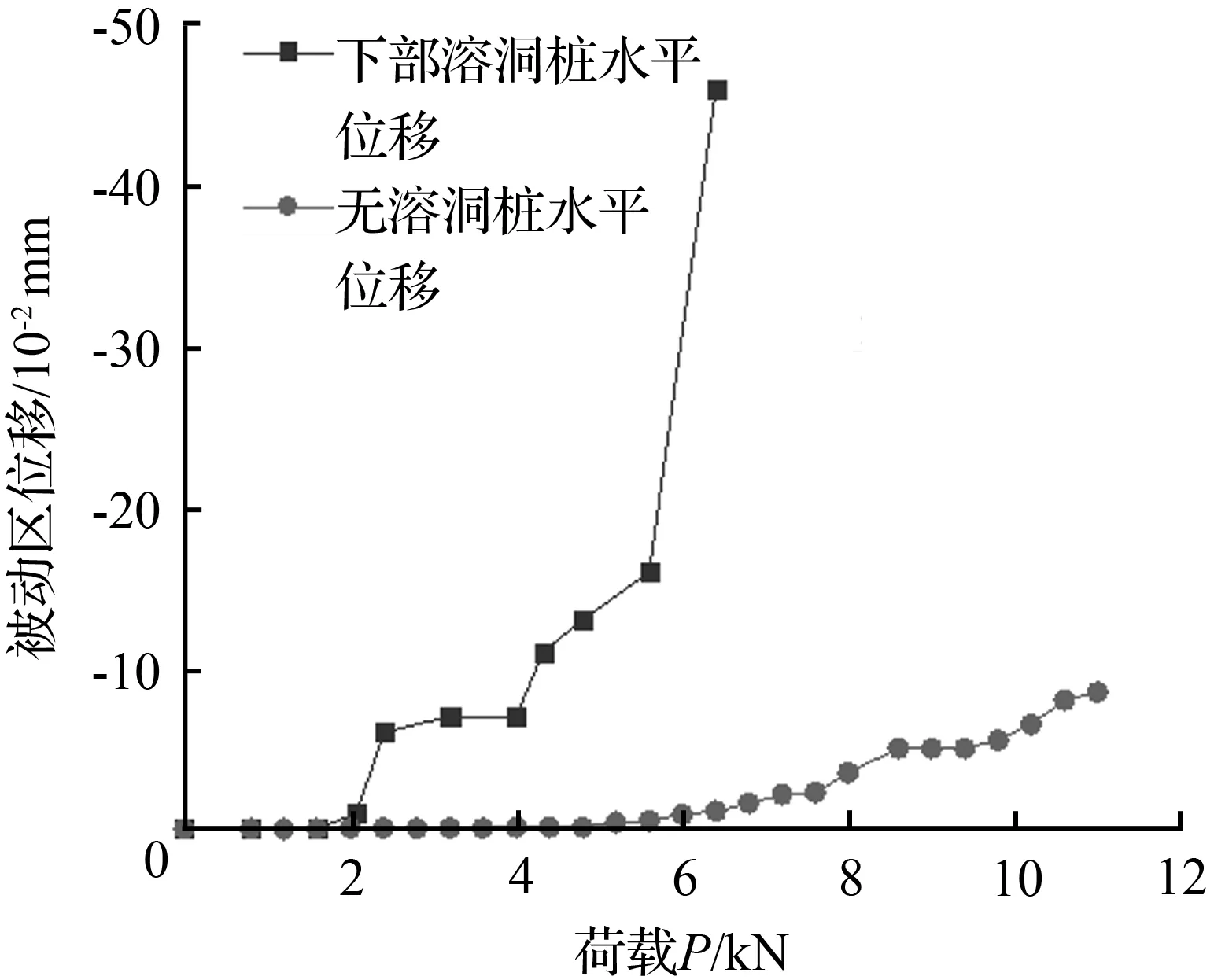
(b) 荷载—主动区位移曲线

分析图8中相关曲线得到如下结论：

① 在水平荷载作用下，无溶洞模型和下部有溶洞模型的主动区和被动区所反映的特征相同，均为主动区升高被动区降低，且被动区的降低程度比主动区的升高程度更大；

② 无溶洞模型和下部有溶洞模型主动区位移在水平荷载超过2 kN时增长较快，下部有溶洞模型被动区变形增加迅速，而无溶洞模型随荷载增加相对缓慢；被动区P-S曲线偏离程度远大于主动区P-S曲线，说明下部存在溶洞时，水平荷载作用对被动区影响远大于主动区；对比无溶洞时主动区和被动区P-S曲线，相同荷载下主动区位移是被动区位移的1.8倍，说明在荷载作用对主动区变形影响较大；

③ 当荷载达到6.4 kN(下部有溶洞模型破坏荷载前一级荷载)时，下部有溶洞与无溶洞模型抗滑桩的水平位移之比为1.27，主动区位移之比为0.99，被动区位移之比为41.82。即同等荷载作用下，溶洞加剧了抗滑桩的水平位移和桩周被动区位移变形。

2.3 荷载—孔径位移分析

为量测试验过程中溶洞孔径的变化情况，在溶洞内置入孔径位移计，分别量测长轴方向与短轴方向的孔径变形，伸长为正，反之为负，所测孔径变形结果如图9所示：

(a) 短轴方向位移

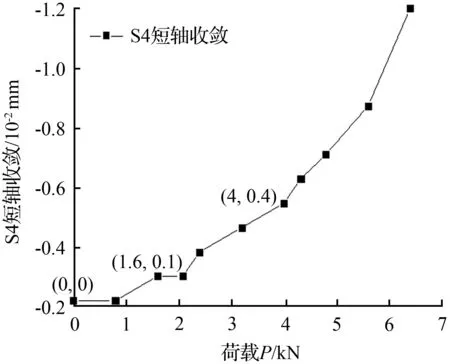
(b) 长轴方向位移

图9 下部有溶洞模型荷载—孔径位移曲线

Fig.9 Load-Aperture displacement diagram of the lower-part karst cave model

分析图9中短轴和长轴方向位移曲线可知：

① 溶洞短轴方向发生伸长变形，而长轴方向发生收缩变形，长、短轴均随着荷载的增加变形逐渐增大；

② 在同时期荷载下短轴方向变形是长轴方向变形的3倍，说明荷载对短轴方向变形影响较大。

2.4 应变值规律分析

为获取桩端嵌岩段岩体在荷载作用下的应变规律，在模型侧面布设20个45°箔式应变花。粘贴应变花之前，用砂纸、无水乙醇和医用棉球将测量区域进行表面处理，将模型和应变花用502胶水粘贴，最后用环氧树脂进行密封，静置24 h待环氧树脂完全凝结硬化。选取无溶洞模型11 kN和下部有溶洞模型6.4 kN的最大主应变云图如图10和图11所示:

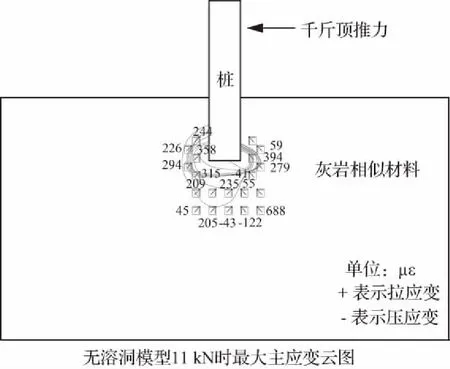
图10 无溶洞模型最大主应变云图

Fig.10 Maximum principal strain images of no-cave model

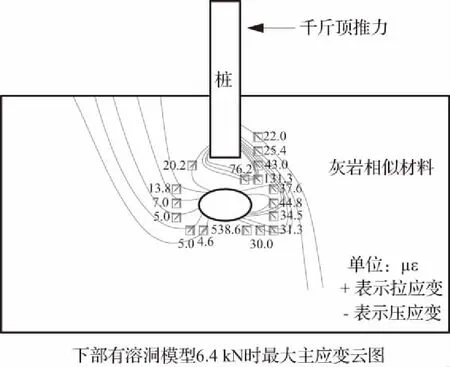
图11 下部有溶洞模型最大主应变云图

Fig.11 Maximum principal strain images of lower-partkarst cave model

对比图10和图11中最大主应变云图规律可得以下结论：

① 两个模型抗滑桩桩脚处应变值规律基本一致，应力集中在桩脚两侧，主动区相对密集而被动区相对稀疏，且主区密集程度更大；荷载较大时，无溶洞模型桩下离桩底较远处产生压应变，而较近处产生拉应变；下部有溶洞模型则全为拉应变；两个模型桩底岩体应变值均较大，可知岩体处于最不利受力状态，导致模型主动区侧出现裂纹并最终使模型发生脆性破坏。

② 溶洞周围存在明显的应力集中，局部应变较大；下部有溶洞模型溶洞周边最大主应变数值较无溶洞模型相同位置处更大，说明在同等荷载下，溶洞的存在使其周边岩体的变形更大，更容易导致抗滑桩嵌固段发生脆性破坏从而导致抗滑桩失稳。

2.5 声发射分析

荷载作用下，材料内部产生应变，当材料内部应变超过其本身允许变形时材料发生破坏，进而产生瞬态弹性波，此现象被称为声发射[15]。声发射广泛的应用于各种岩体破坏研究中，此次试验采用AE绝对能量探究模型的内部破坏情况。无溶洞模型和下部有溶洞模型相应的声发射AE绝对能量曲线与荷载图如图12和图13所示。

图12 无溶洞模型AE绝对能量与荷载曲线图

Fig.12 AE absolute energy and load curve of no-cave model

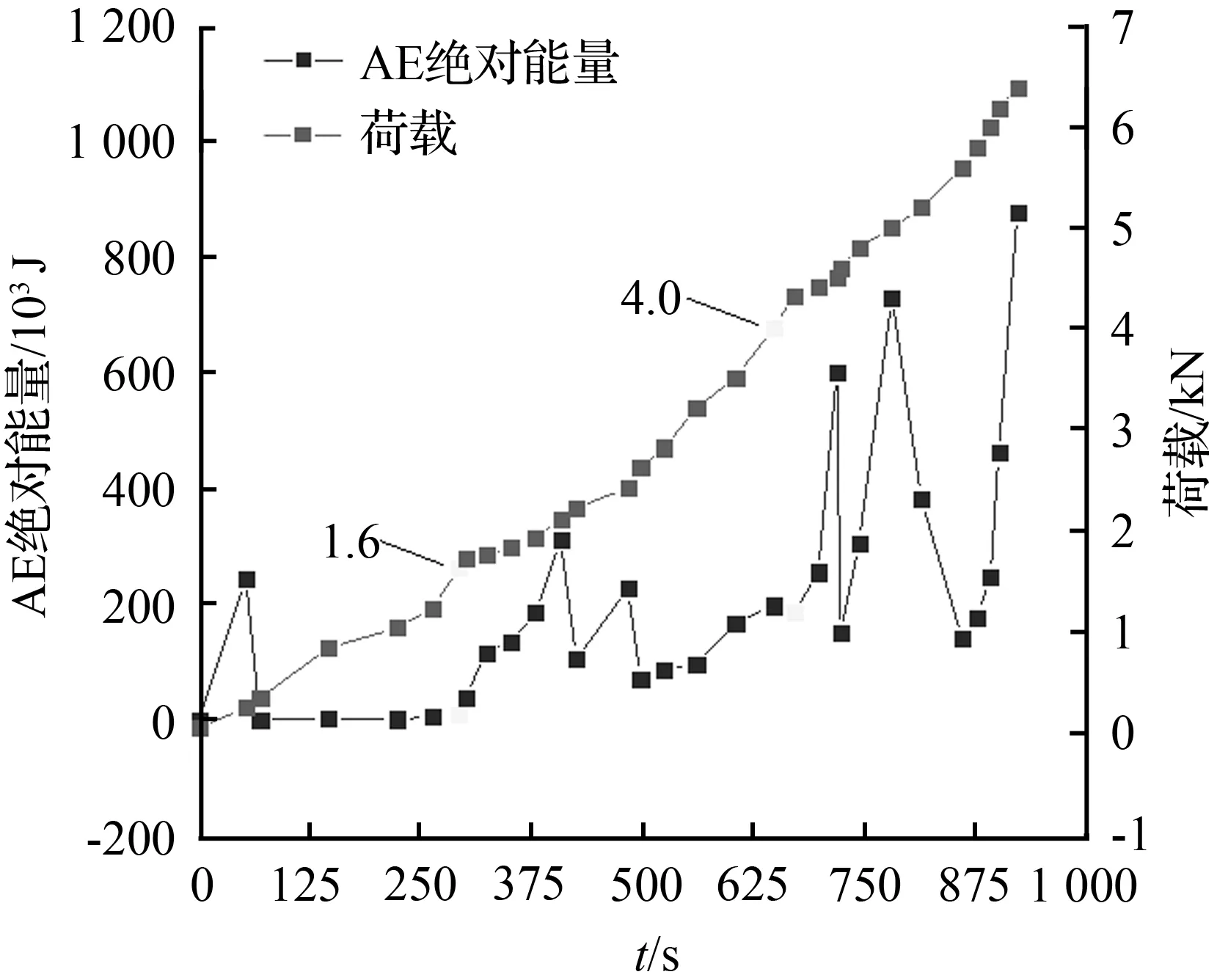
图13 下部有溶洞模型AE绝对能量与荷载曲线图

Fig.13 AE absolute energy and load curve of lower-partkarst cave model

对比图12和图13可得到：

两个模型的声发射曲线均可分成三个阶段考虑：两个模型在各自约1/4倍极限荷载之前，AE绝对能量值较低，声发射现象较少；当荷载处于约1/4～2/3倍极限荷载时，模型内部时刻产生微小裂纹，AE绝对能量值相对较高，声发射现象较为密集；在极限荷载2/3倍以上时，AE绝对能量值较高，声发射现象密集，模型内部已经产生的微小裂纹逐渐连通，同时伴随着新的微小裂纹的产生，随着模型加载达到破坏荷载，模型内部裂纹瞬间贯通，模型最终发生脆性断裂。