基于阿克曼原理的三轴车辆全轮转向最优控制
2020-07-13陆海英张成铭郭艳秋王雨琪杨蔡进
陆海英,张成铭,郭艳秋,王雨琪,杨蔡进*
(1.中车长春轨道客车股份有限公司, 吉林 长春 130062;2.西南交通大学 牵引动力国家重点实验室, 四川 成都 610031)
0 引言
当前对于多轴车辆的运用越来越普遍,传统的多轴车辆只有前轴转向,车辆低速时的转向灵敏性和高速时的操纵稳定性较差[1-2],研究多轴转向控制技术有利于优化车辆的操纵稳定性。以三轴车为控制对象的研究中,文献[3]将三轴车辆在低速与高速运行时的控制目标独立开来,分别建立相应的目标模型,并以此建立全轮转向LQR模型;文献[4]设计了三轴车辆电控转向系统,并且在传统的零侧偏角比例控制的基础上引入鲁棒控制;文献[5]设计的全轮转向滑膜控制器,相比于传统的多轴转向最优控制器,其对于外界环境变化的抗扰性更好;文献[6]针对车辆在极限工况下,车轮侧向力不足的情况,设计了基于分层控制理论的水平集成控制器,并且达到了预期的控制效果;文献[7]为了提高控制系统对于车辆模型参数变化的适应性和鲁棒性,提出了基于MPC理论的三轴车全轮转向控制模型;文献[8]从工程应用的角度出发,分别对比了车辆的后两轴与第一轴的5种不同的转角比例关系下的转向模式,并且通过仿真结果说明了车辆在各种运行工况下,不同转向模式的适应性;文献[9]建立了车辆2DOF模型,模型中采用逆向估计的方式动态计算轮胎的侧偏刚度,基于建立的车辆模型设计了6WS + DYC集成控制策略,并且以建立的10自由度非线性车辆模型为控制对象,验证了控制模型的有效性。除此之外,文献[10]针对四轴全轮转向车辆提出了一种基于车轮转角比例前馈+横摆角速度反馈的最优补偿控制算法;文献[11]考虑五轴车辆转向时,转动中心位置变化对车辆转向性能的影响,设计了PID-D控制策略,并通过与固定D值转向方式进行对比,验证了PID-D控制策略对于提高多轴转向车辆操纵稳定性的有效性。
现有的全轮转向控制研究,都只重点研究针对车辆操纵稳定性的优化效果,并没有着重去研究对于车辆轮胎磨损的影响,本文在传统全轮转向最优控制的基础上,考虑减小车辆在转动过程中轮胎的磨损,根据阿克曼转向几何原理[12],建立全轮转向最优控制模型,并与传统全轮转向控制方法进行对比,通过分析车轮的轮胎力和滑移率响应曲线验证了基于阿克曼原理的全轮转向最优控制策略对于减小车辆在转向时的轮胎磨损程度是有利的。
1 三轴全轮转向车辆模型
1.1 单轨车辆二自由度动力学模型
为研究车辆在转弯的过程中操纵稳定性变化[13]的基本特征,建立简化的三轴车辆2DOF模型如图1所示。

图1 三轴车辆2DOF模型
各变量定义如下:m为整车质量;Iz为车辆横摆转动惯量;u为车辆质心纵向速度;v为车辆质心侧向速度;ω为车辆质心横摆角速度;β为车辆质心侧偏角;a,b,c为车辆质心到各轴的距离;ε1,ε2,ε3分别为各轴车轮轮速u1,u2,u3与x轴的夹角;δ1,δ2,δ3分别为各轴车轮转角;Fy1,Fy2,Fy3分别为车辆各轮侧向力;α1,α2,α3分别为各轮侧偏角;K1,K2,K3分别为各轮侧偏刚度。
则根据图1,可以建立微分方程为:
(1)
1.2 TruckSim车辆模型
本文选取TruckSim中的一款三轴客车整车模型作为研究对象,模型共27个自由度,将车辆三根轴全部设置为转向轴,车辆的第一轴车轮转角来自于TruckSim内部自带的驾驶员模型,第二、三轴车轮转角则通过Matlab/Simulink外部建立的转向控制模型输入,TruckSim车辆模型的主要参数如表1所示。

表1 TruckSim车辆模型主要参数
2 基于阿克曼原理的全轮转向最优控制

图2 车辆各轴车轮转角运动学关系
传统的三轴车全轮转向最优控制策略,在求解各轴车轮转角时,并没有考虑车辆各轴车轮的运动学约束,使得车辆在转向过程中,某个车轮无法实现纯滚动运动,加大了轮胎的磨损。本文基于车辆转动过程中各轴车轮应该满足的阿克曼转向原理,在车辆二自由度动力学模型的基础上,加入车辆各轴车轮的运动学约束,建立最优二次型控制策略。
2.1 车辆各轴车轮运动学约束
本文基于阿克曼原理,采用向量法推导车辆各轴车轮应该满足的关系。根据建立的车辆2DOF模型,并定义车辆瞬时转动中心为P(x,y, 0),可以得到车辆转向时各轴车轮应该满足的运动学关系如图2所示。
根据直线AP和直线BP可以得到点P的坐标为:
(2)
由点B和点P可以得到向量b2为:
(3)
则向量h2可以计算得到:
(4)
通过向量h2可以计算得到车辆第二轴转角为:
(5)
在车辆三个轴的车轮转角均较小的情况下,可假设:
(6)
则式(5)可以简化为:
(7)
为了验证式(6)的合理性,当车辆第一、三轴转角在-20 deg到20 deg的范围变化时,对比由式(5)和式(7)计算得到的车辆第二轴车轮转角误差如图3所示。

图3 两种方式计算下δ2的误差曲线
由图3可知,由式(5)和式(7)计算得到的第二轴车轮转角误差小于0.4 deg,证明式(6)所做的假设是合理的。
2.2 基于阿克曼原理的全轮转向最优控制
本文以三轴车辆第三轴车轮转角作为最优控制的控制输入,而车辆第二轴车轮转角则根据车辆运动学约束计算得到,所以将式(7)代入到式(1),并以β和ω为状态变量,可以得到车辆状态空间方程为:
(8)

定义车辆理想状态变量如下:
(9)
以车辆理想状态变量和实际状态变量的差异最小为优化目标,且保证输出的车辆后轮转角最小,建立目标函数如式(10)所示:
(10)
式(10)为一个带有等式约束的最优目标函数,通过引入向量λ将式(10)转化为无约束的目标函数(11):
(11)
令:
(12)
将式(12)代入(11)得到:
(13)
根据变分法求解式(13),当式(13)取得极小值时:
(14)
由式(14)第二项可以得到最优控制量:
U*=-R-1BTλ,
(15)
将式(15)变换为包含状态变量X的方程,令:
λ(t)=P(t)X(t)+ε(t),
(16)
对式(16)求导得到:

(17)
由前式可以得到:
(18)
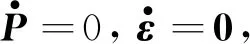
(19)
式(19)第一项称为黎卡提方程[14],求解该方程可以得到矩阵P的唯一解,将式(19)代入式(15)可以得到最优控制量:
U*=-R-1BTPX-R-1BT(AT-PBR-1BT)-1(QAd-PC)δ1。
(20)
基于阿克曼原理的三轴车全轮转向最优控制流程如图4所示。

图4 基于阿克曼原理的三轴车全轮转向最优控制流程
3 仿真建模与分析
在TruckSim中输入命令OPT_DRIVER_ACTION=0,屏蔽掉TruckSim中驾驶员模型对车辆模型的转向控制作用,并将方向盘转角输出到Matlab/Simulink中,通过Matlab/Simulink建立的控制模型计算得到车辆各轴车轮的等效转角,用于控制TruckSim车辆模型转向。其中,Matlab/Simulink中建立的最优控制模型相关参数如表2所示。

表2 最优控制模型相关参数

图5 圆和直线组成的复合轨迹
分别建立只考虑车辆质心侧偏角和横摆角速度响应的三轴车全轮转向最优控制模型和考虑阿克曼原理的全轮转向最优控制模型,考虑到式(7)所表示的车辆各轴车轮之间的关系,是在车辆低速的情况下满足的,高速时由于轮胎速度偏角的存在,车辆各轴车轮之间不再满足式(7),本文选取车辆车速为20 km/h时,行驶双移线轨迹以及由圆弧和直线组成的复合轨迹两种仿真工况,其中,由圆弧和直线组成的复合轨迹如图5所示。考虑到车辆轮胎磨耗是跟车轮受到的轮胎力和滑移率[15]相关的,所以对比两种最优控制策略下车辆各状态响应以及轮胎受到的力和滑移率曲线。
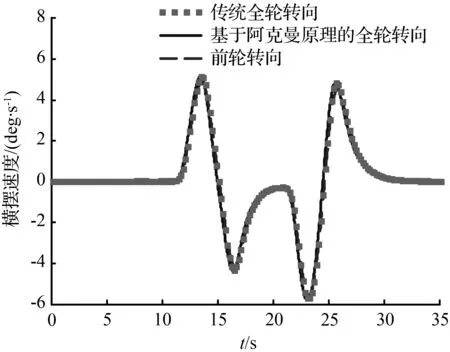
图6和图9分别对比了双移线轨迹以及圆和直线组成的复合轨迹两种工况下车辆的状态响应曲线,通过两种工况下的仿真结果可以得到相同的结论,由图6(a)和图9(a)可知,基于阿克曼原理的全轮转向最优控制下的车辆质心侧偏角最小,而由图6(b)和图9(b)可知,三种转向方式下的车辆横摆角速度响应基本一致,表明,全轮转向最优控制下的车辆的操纵稳定性得到了提高。
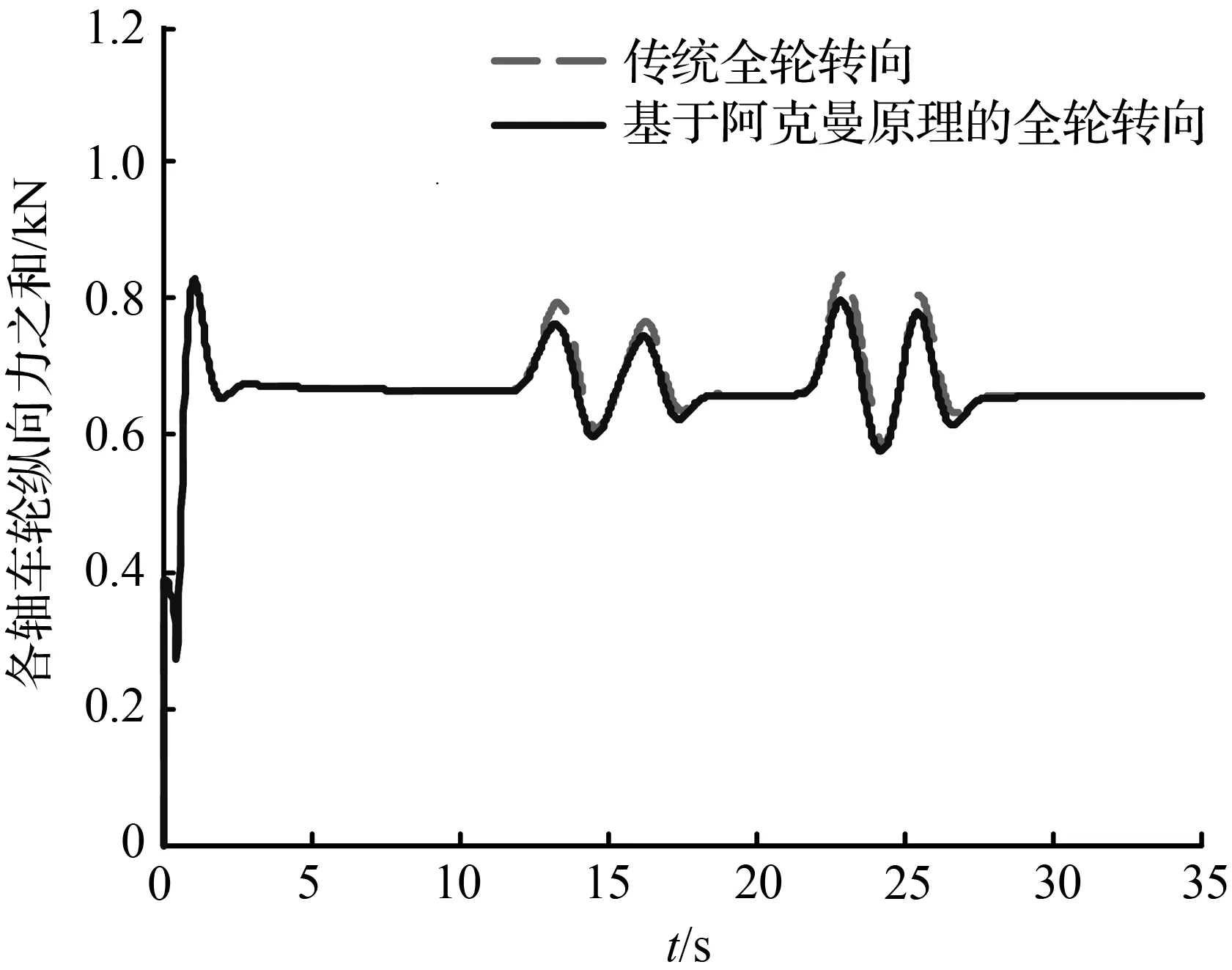
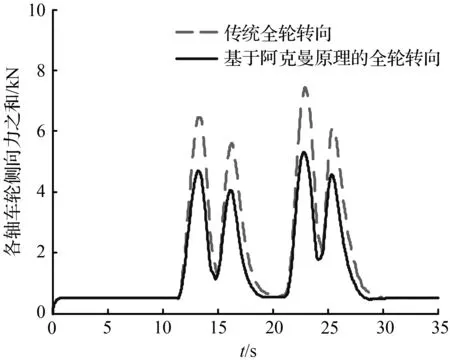
图7和图10分别对比了双移线轨迹以及圆和直线组成的复合轨迹两种工况下车辆的轮胎受力之和响应曲线,由图7和图10对比可知,基于阿克曼原理的全轮转向最优控制下的车辆轮胎受到的纵向力和侧向力之和均变小了,但是相比于双移线轨迹,在圆和直线组成的复合轨迹下,车辆转弯时的转向角更大,传统全轮转向车辆的车轮在纵向方向上和侧向方向上发生的滑动程度更大,所以在此种工况下,基于阿克曼原理的全轮转向车辆相比于传统的全轮转向车辆,其轮胎产生的纵向力和侧向力之和减小的程度更大,对于车辆轮胎磨损的缓解效果更加明显。
图8和图11分别对比了双移线轨迹以及圆和直线组成的复合轨迹两种工况下车辆的滑移率曲线,由图8(a)、图8(b)、图11(a)和图11(b)可知,两种全轮转向最优控制下的第一轴车轮滑移率基本一致,这是因为车辆的第一轴车轮转角由TruckSim软件自带的驾驶员模型计算得到,在同样的目标轨迹下,两种全轮转向控制下的车辆第一轴的车轮转角基本保持一致。基于阿克曼原理的全轮转向最优控制主要约束车辆的第二轴车轮转角,所以,由图8(c)、图8(d)、图11(c)和图11(d)可以看出,相比于传统全轮转向,基于阿克曼原理的全轮转向控制下车辆的第二轴的左右轮滑移率减小的程度最大,同时,该控制下车辆的第三轴的左右轮滑移率也有一定程度的减小。同理,在车辆车轮大转角的工况下,基于阿克曼原理的全轮转向最优控制下车辆各轴的左右轮滑移率减小的程度更大。

(a) 质心侧偏角
(b) 横摆角速度
图6 双移线轨迹下车辆状态响应曲线
Fig.6 Vehicle state response curve under double line change
(a) 各轴车轮纵向力之和
(b) 各轴车轮侧向力之和
图7 双移线轨迹下车辆各轴车轮受力之和
Fig.7 Sum of vehicle tire forces under double line change
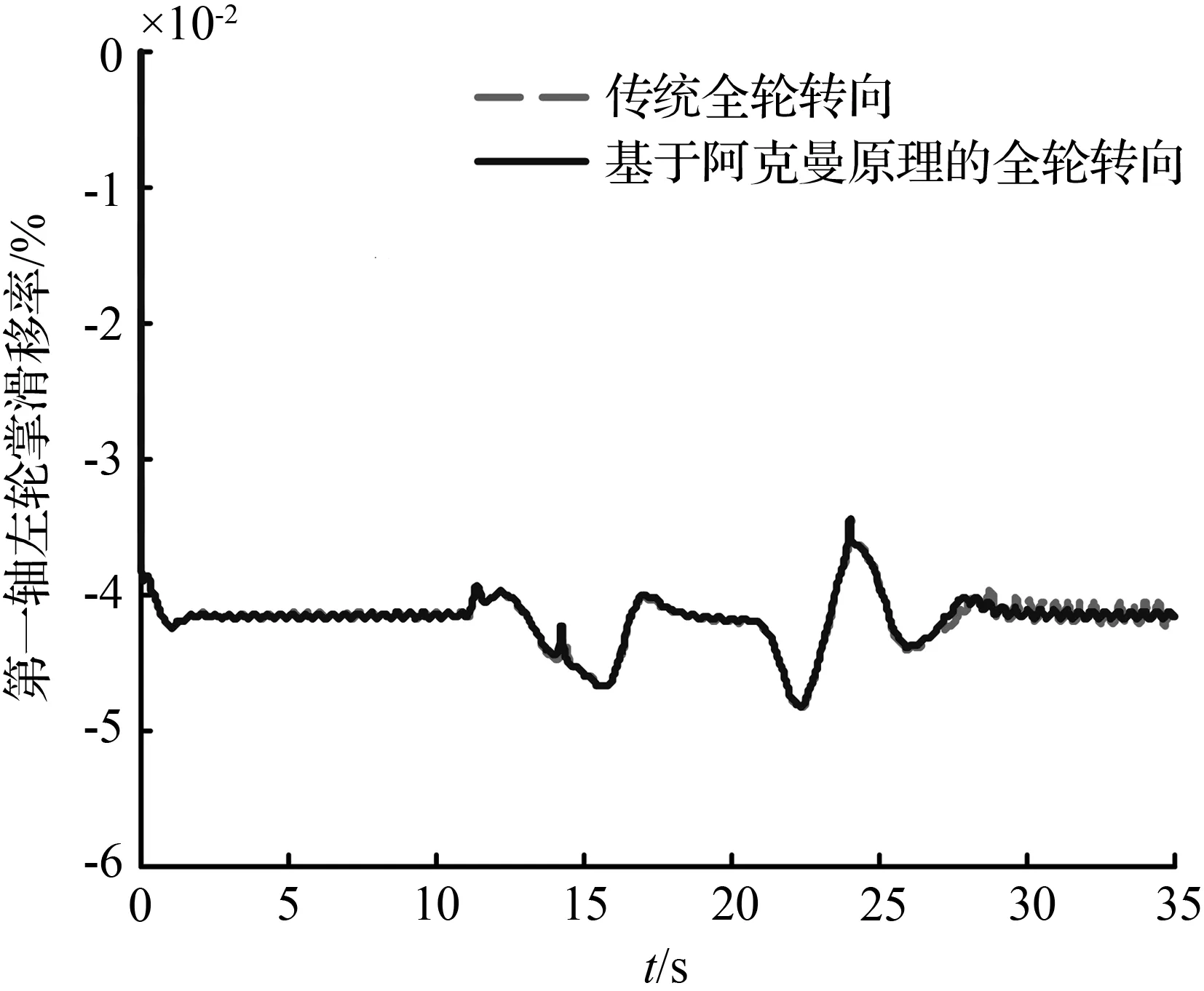
(a) 第一轴左轮滑移率
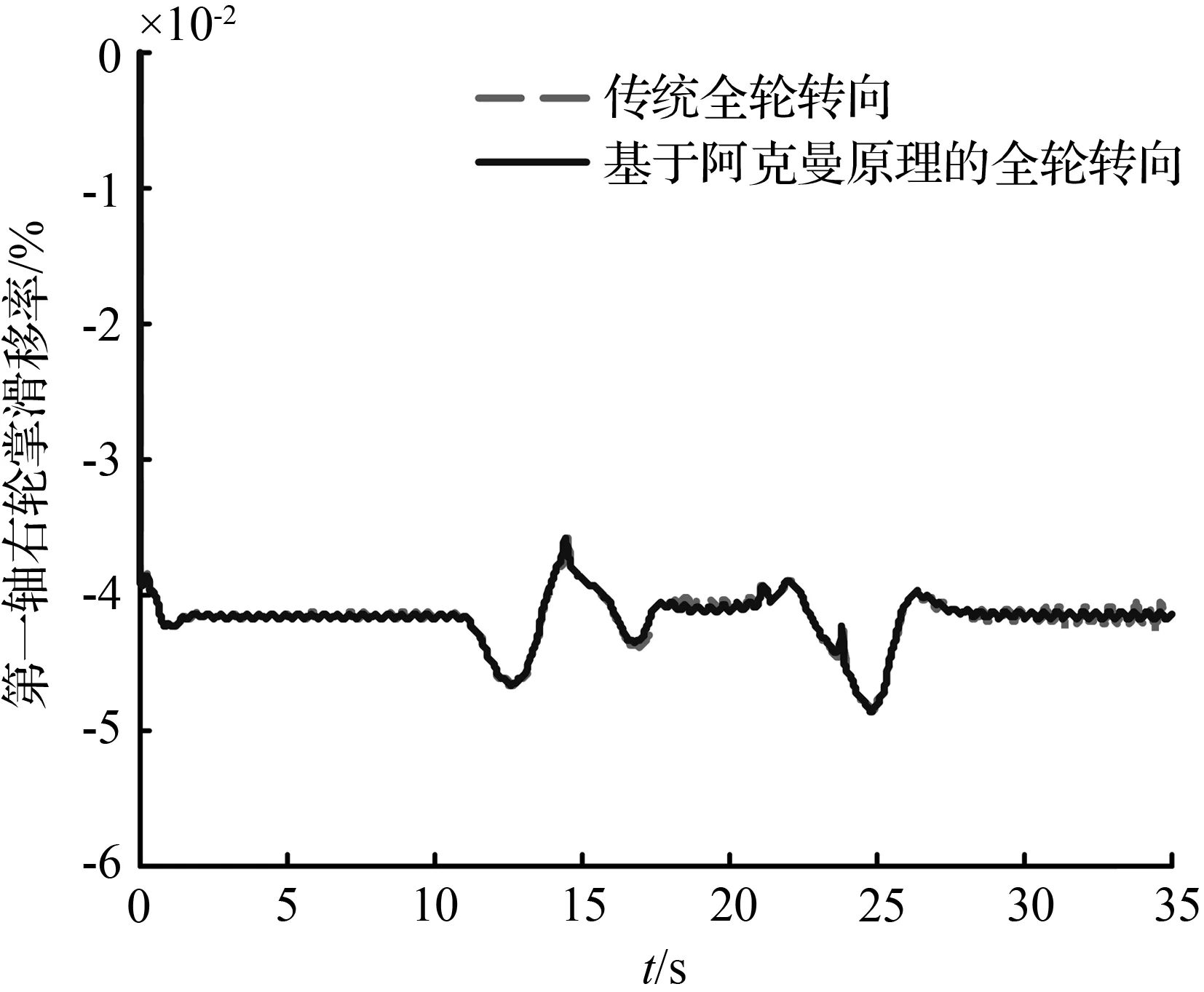
(b) 第一轴右轮滑移率

(c) 第二轴左轮滑移率

(d) 第二轴右轮滑移率

(e) 第三轴左轮滑移率

(f) 第三轴右轮滑移率
图8 双移线轨迹下轮胎滑移率曲线
Fig.8 Tire slip ratio curve under double line change

(a) 质心侧偏角
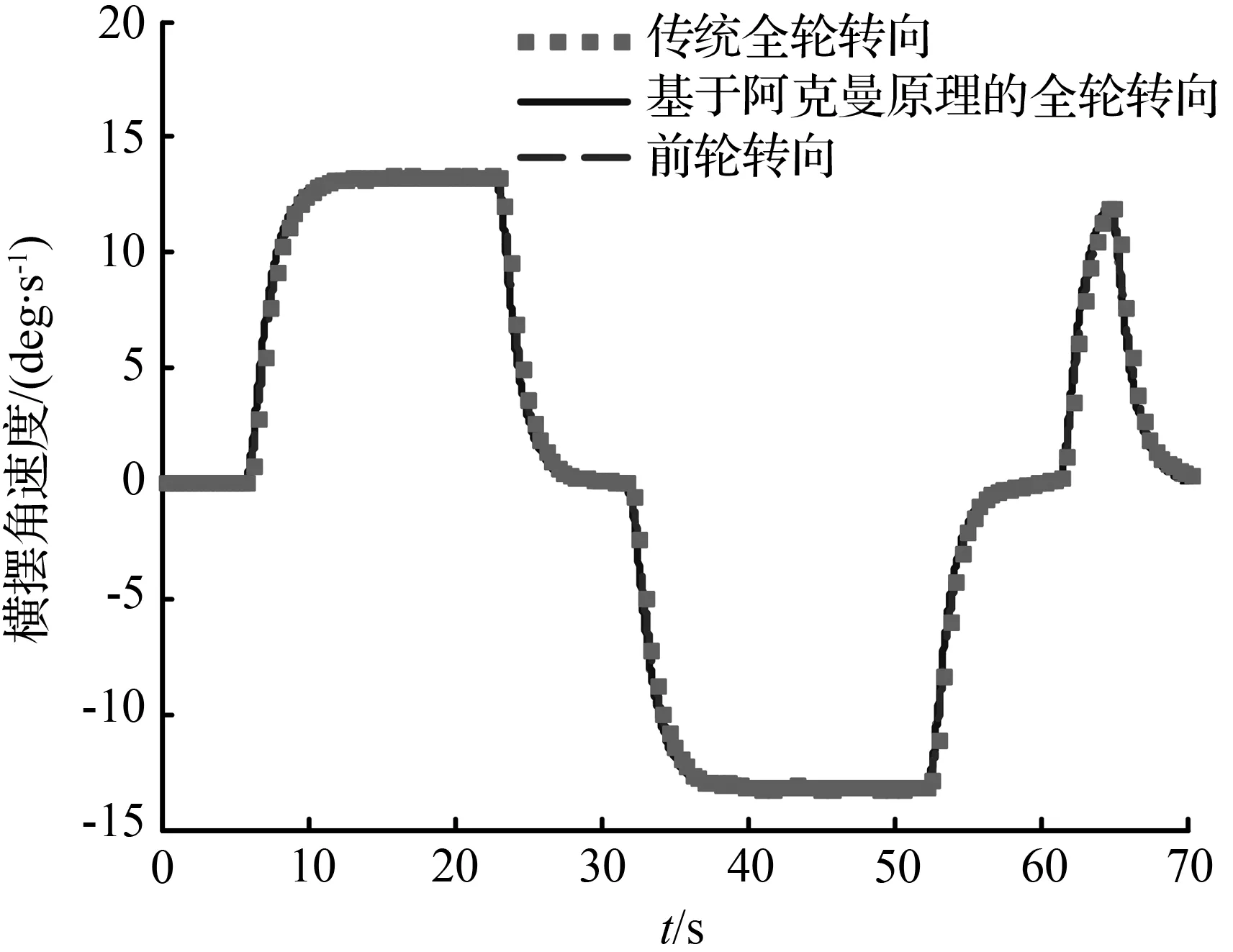
(b) 横摆角速度
图9 复合轨迹下车辆状态响应曲线
Fig.9 Vehicle state response curve under compound track
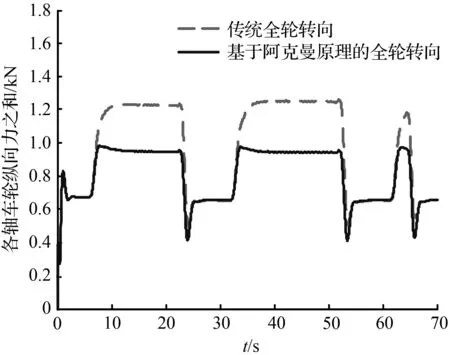
(a) 各轴车轮纵向力之和

(b) 各轴车轮侧向力之和
图10 复合轨迹下车辆各轴车轮受力之和
Fig.10 Sum of vehicle tire forces under compound track
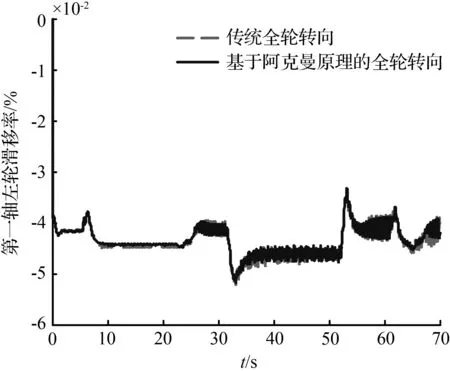
(a) 第一轴左轮滑移率
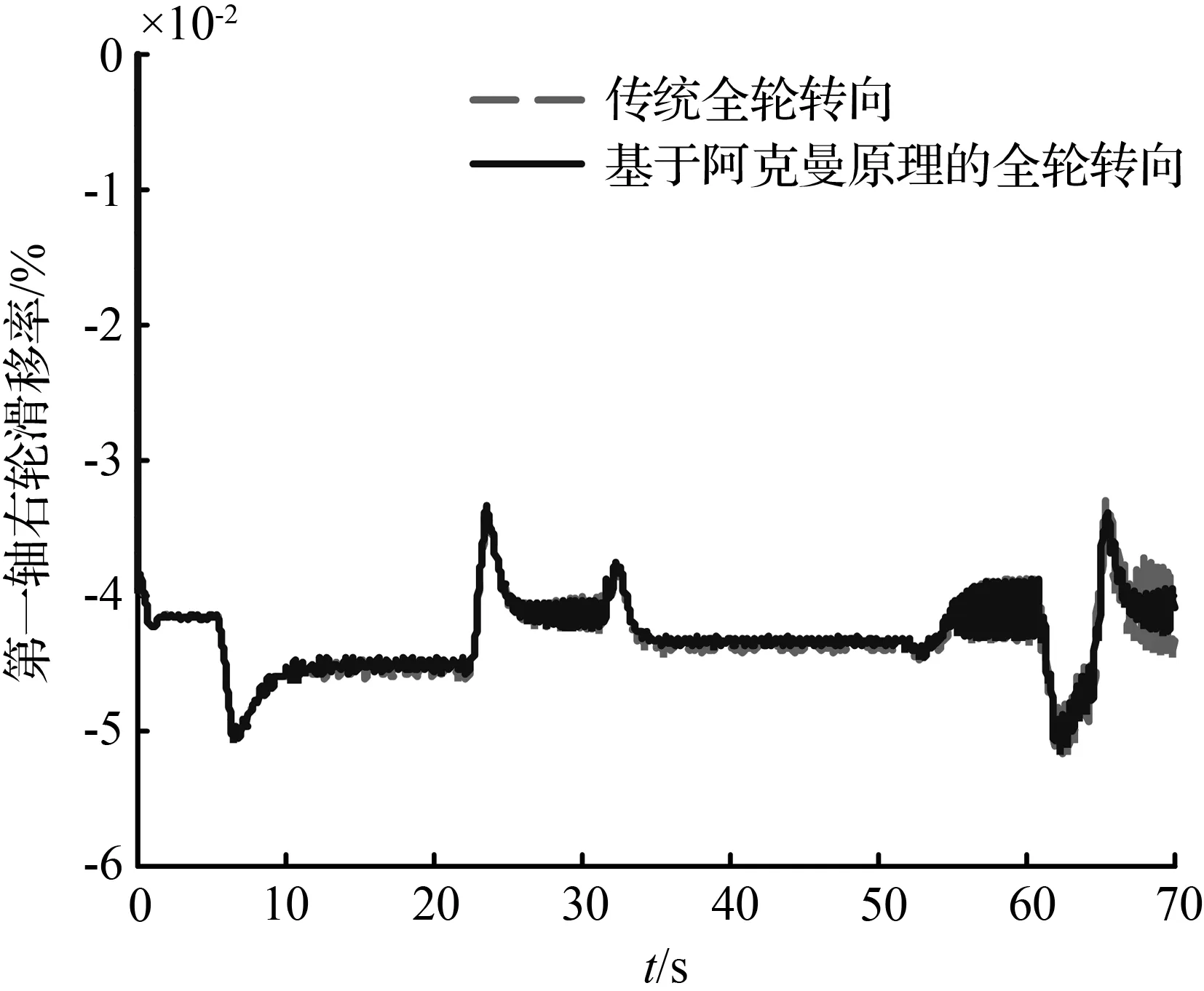
(b) 第一轴右轮滑移率

(c) 第二轴左轮滑移率
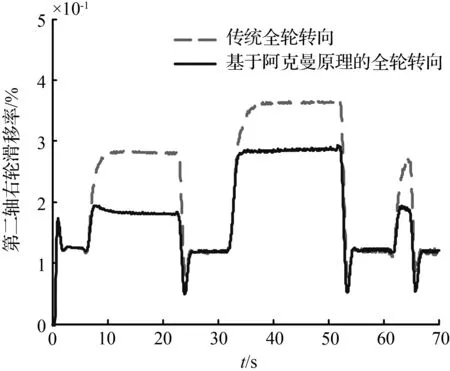
(d) 第二轴右轮滑移率
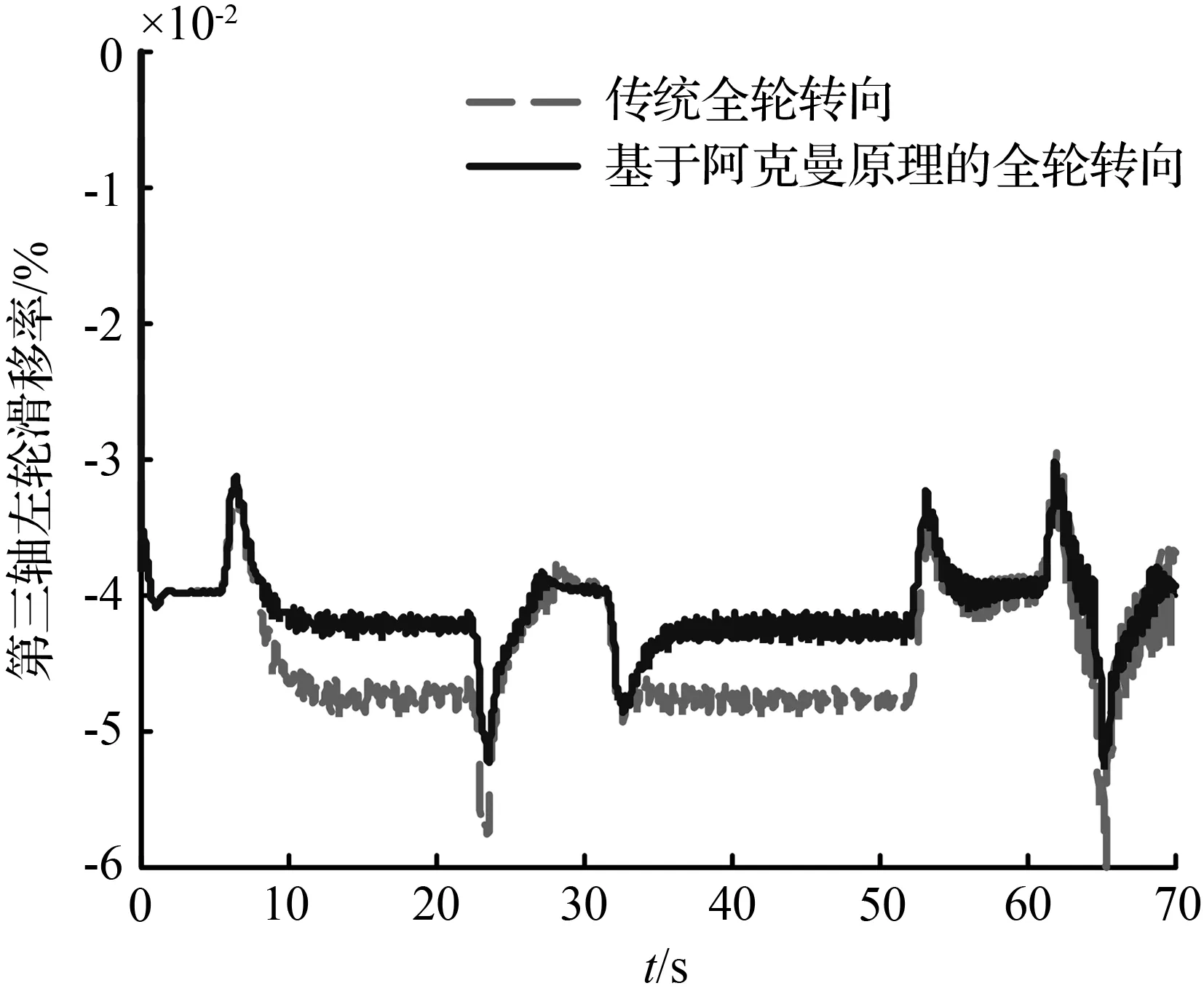
(e) 第三轴左轮滑移率

(f) 第三轴右轮滑移率
图11 复合轨迹下轮胎滑移率曲线
Fig.11 Tire slip ratio curve under compound track
4 结语
① 本文以三轴车辆为研究对象,基于阿克曼转向原理,建立各轴车轮转向运动学约束关系。将质心侧偏角和横摆角速度参考值作为跟踪目标,建立基于阿克曼原理的三轴车辆全轮转向操作稳定性的最优控制模型。采用Matlab/Simulink和Trucksim软件搭建联合仿真平台,对传统全轮转向和基于阿克曼原理全轮转向操作稳定性控制进行仿真研究和对比分析。
② 相比于传统全轮转向,基于阿克曼原理的全轮转向最优控制能获得更优异的操作稳定性能,即在相同工况下,质心侧偏角和横摆角速度能得到更有效地控制。同时,基于阿克曼原理全轮转向控制方法使纵向轮胎力、侧向轮胎力以及轮胎滑移率更小,有利于减小轮胎磨损,提高各轴车轮的协同转向性能。
③ 针对低速大转角是三轴车辆行驶过程中的典型工况,仿真研究表明,当车辆的转向角越大时,基于阿克曼原理的全轮转向最优控制,对于减小轮胎磨损越明显。因此,在三轴车辆操纵稳定性控制设计时,考虑各轴车轮满足同一转动瞬心原则,以提高各轴车轮的转向协同性能和减小轮胎磨损是很有必要的。
