基于DEA的长江经济带工业用水效率评价

尹佳佳，黄云梅，唐 敏

（重庆师范大学数学科学学院，重庆 401331）

引言

长江经济带地处长江流域，包含上海、江苏、浙江、安徽、江西、安徽、江西、湖北、湖南、重庆、四川、云南、贵州11省市，覆盖面积占全国的21.4%。长江经济带作为我国最重要的工业走廊之一，集中了大量钢铁、电子、汽车等工业产业，大多工业企业都是属于粗放型的生产方式，在产生经济效益的同时造成了不可逆的环境污染。随着我国工业化与城镇化的加快，长江经济带工业用水量增多，其工业废水、废弃、固体废物排放量也持续增长，特别是水资源污染越发的严峻，故对长江经济带工业用水效率进行评价，为改善工业用水现状提出建议是十分必要的。

当前有许多学者对用水效率进行了研究，通常采用层次分析法［1-2］、模糊评价法［3］、SFA方法［4］、DEA方法［5-7］等测算用水效率，其中用得最多的方法是数据包络法。Wang等［8］把化学需氧量和氨氮作为非期望产出，利用SBM模型对中国各省2009-2010年的工业用水效率进行了测算，发现我国各地区在节水减排方面存在着差异。马海良［9］基于2003-2013年我国30个省市的面板数据，采用ML生产率指数法测算了绿色水资源利用效率；程永毅［10］等利用成本效率DEA模型测算了我国2002-2011年工业用水效率，发现地区间效率值有较大差异；海霞等［11］利用超效率DEA模型对京津翼城市群不同行业的用水效率进行了测算；李静、马潇璨［12］采用 SBM-Undesirable和 Meta-frontier对我国工业用水效率进行了评价；Xu Rongrong等［13］采用四阶段DEA方法计算了中国工业用水效率。

分析上述文献可以发现，在研究用水效率时，部分学者没有考虑到废水、废气等非期望产出指标，有的学者虽然考虑到了非期望产出指标，但将非期望产出作为投入进行计算，这种做法不准确；并且很多学者仅仅对工业用水效率进行了静态测算，没有从动态角度对效率值进一步测算，评价不够全面。故本文把环境因素加入指标体系，考虑到工业废水排放对环境的污染，将工业废水中的化学需氧量作为非期望产出指标，建立工业用水效率评价指标体系，并且考虑到随机冲击对效率测算的影响，采用基于非期望产出的SBM-DEA模型对长江经济带工业用水效率进行静态测算，并用bootstrap法纠偏以得到更真实的效率值；再采用Malmquist-Luenberger指数对长江经济带工业用水全要素生产率进行动态测算及分解，最后结合长江经济带的具体实际情况提出建议。

1 工业用水效率评价指标体系建立

根据建立评价指标体系需要遵循的全面系统原则、可操作性原则、科学可行性原则，以及数据包络分析法需满足投入产出指标之和小于所有决策单元（DMU）的二分之一的要求，本文将环境污染作为非期望产出指标加入指标体系，共选择三个投入指标、两个产出指标建立指标体系，见表1。

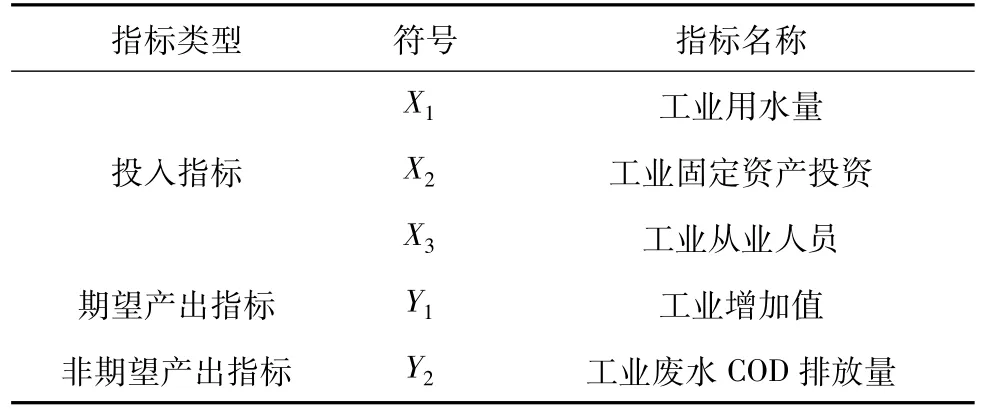
表1 工业用水效率评价指标体系

本文对长江经济带2010-2016年的工业用水效率进行评价，所选指标数据均来自于2011-2017年的《中国统计年鉴》、《中国环境统计年鉴》以及长江经济带各省市的统计年鉴。

2 模型构建

数据包络分析法是由运筹学家A.Charnes和W.W.Copper提出的以相对效率为基础的多项指标投入和多项指标产出的系统分析方法［14］。DEA方法无需事先设定指标权重，每项权重都是由输入、输出数据确定出来的最优权重，故具有很强的客观性，适合评价多种效率问题。DEA方法中最基本的模型是CCR模型及BCC模型，由于传统DEA没有考虑到投入或产出要素的松弛性问题，也无法对非期望产出指标进行处理，用其计算出来的结果与真实值存在一定的偏差。而工业生产中不仅有期望产出，还有水环境污染等非期望产出，将非期望产出加入模型进行计算可使结果更接近真实值，故本文采用Tone［15］提出的非径向非角度的 SBM（Slack-Based Measure）模型对长江经济带工业用水效率进行静态测算。

2.1 基于非期望产出的SBM模型

假设有n个决策单元，每个决策单元有m项投入变量x=（x1j，x2j，...，xmj），s项产出变量，包含a个期望产出变量ya=（，b个非期望产出变量（，其中xj＞0，yj＞0。

生产技术集定义为：

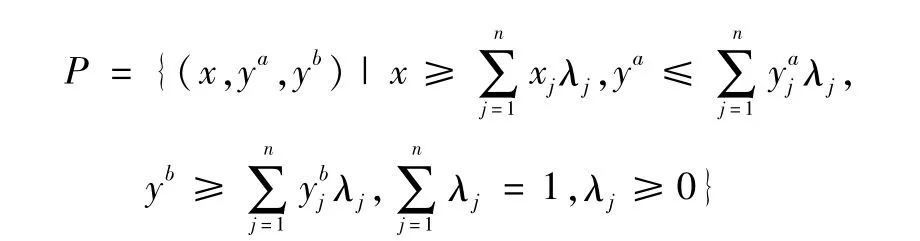
加入非期望产出的SBM模型如下：

其中：ρ为效率值；s-、sa、sb分别为投入、期望产出、非期望产出的松弛量；λ为权重向量。当ρ=1且s-=0，sa=0，sb=0时，称该DMU是有效的；当 ρ＜1，则该DMU无效。

2.2 bootstrap修正SBM

由于采用SBM-DEA模型是对有限的观察值进行测算的，其测算结果会受到随机因素的干扰，易受到极端值的影响，使得测算值与实际值存在一定偏差。故借鉴Simar和Wilson［16］将Bootstrap方法引入 DEA模型的思想，采用Bootstrap法修正效率值，得到更真实、可信度更高的效率值。其基本步骤如下：

（1）将基于非期望产出的SBM模型测算出的决策单元效率值 θ′=（θ′1，θ′2，…，θ′M）作为 bootstrap-DEA的原始样本数据。

（2）采用重复有放回的抽样方法，从原始样本数据θ′中抽取一个相同数量的naive bootstrap样本θ=（θB1，θB2，…，θBM），并对其进行平滑处理，得到新的样本数据

（3）利用得到的新样本 θ*=（）对原始投入样本数据进行调整，调整公式如下：

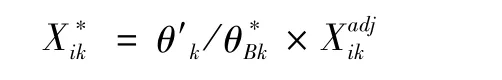
其中，i=1，2，…，n，k=1，2，…，M，是经过bootstrap调整后第k个决策单元的第i个投入要素值。

（4）重复（2）和（3）B次，则每个评价对象均能得到B个效率得分的估计值：

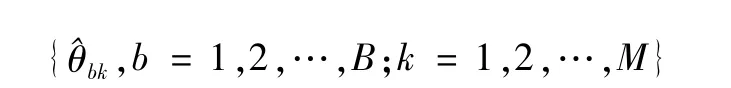
（6）测算各个评价对象的初始效率值θ′k的偏差与偏差修正之后的效率值θ0k。

2.3 ML生产率指数

本文采用Chung等［11］人提出的含有非期望产出的方向距离函数——Malmquist-Luenberger生产率指数对2010-2016年长江经济带工业用水效率进行动态测算。决策单元t到t+1时期的ML指数为：

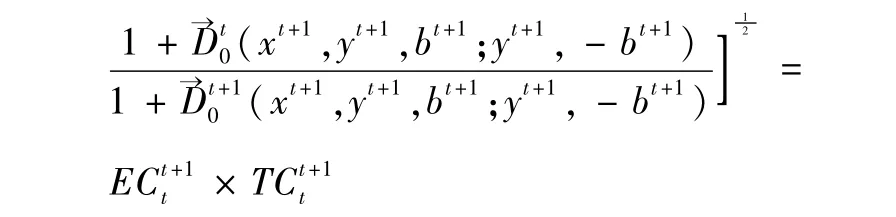
当ML指数大于1时，表明全要素生产率提高；当ML指数小于1时，表明全要素生产率降低；EC为技术效率变化指数，EC大于1，代表该决策单元技术效率提高，EC小于1，表示技术效率降低；TC为技术进步变化指数，TC大于1，表示技术进步，反之退步。

3 实证分析

3.1 长江经济带工业用水效率静态测算

3.1.1 基于非期望产出SBM模型测算值

根据所建指标体系，将长江经济带2010-2016年的面板数据带入基于非期望产出的SBM模型中，使用MaxDEAPro7.6软件进行测算结果见表2。

从表2可以看到，2010-2016年长江经济带的工业用水效率均值为0.7806，说明长江经济带工业用水效率不高，还有很大的提升空间。2010-2016年长江经济带工业用水效率呈现出先增长后下降的形式，在2013年工业用水效率值达到了峰值0.8315，比2012年上升了7.54个百分点。

为进一步对长江经济带区域工业用水效率进行分析，将长江经济带划分为上、中、下游三个区域，重庆、四川、云南、贵州四省组成上游地区，湖北、湖南、江西三省构成中游地区，下游地区包括上海、江苏、浙江、安徽四省。各区域效率值见表3。

从表3可以看出，长江经济带下游地区的平均工业用水效率最高，达到了0.8213；上中游的平均效率值比较接近，中游略高一点为0.7664。这可能是长江下游地区经济水平高，相对于中上游地区有更好的工业生产水平及节水技术，使得其工业用水效率值较高；并且随着社会经济的发展，长江下游的高污染工业产业都向中上游转入，这无疑会导致中上游的效率值偏低。图1表示长江经济带区域工业用水效率值变化情况。从图1可以看出，在变化趋势上，上中下游均呈现出先上升后下降的趋势，其中变化程度最大的是长江经济带上游地区，从2010年的0.6274上升到2016年的0.8415。其原因在于，上游地区是经济最不发达的地区，在早些年没有先进的生产技术，工业多是粗放型生产模式，工业用 水效率提升空间最大。

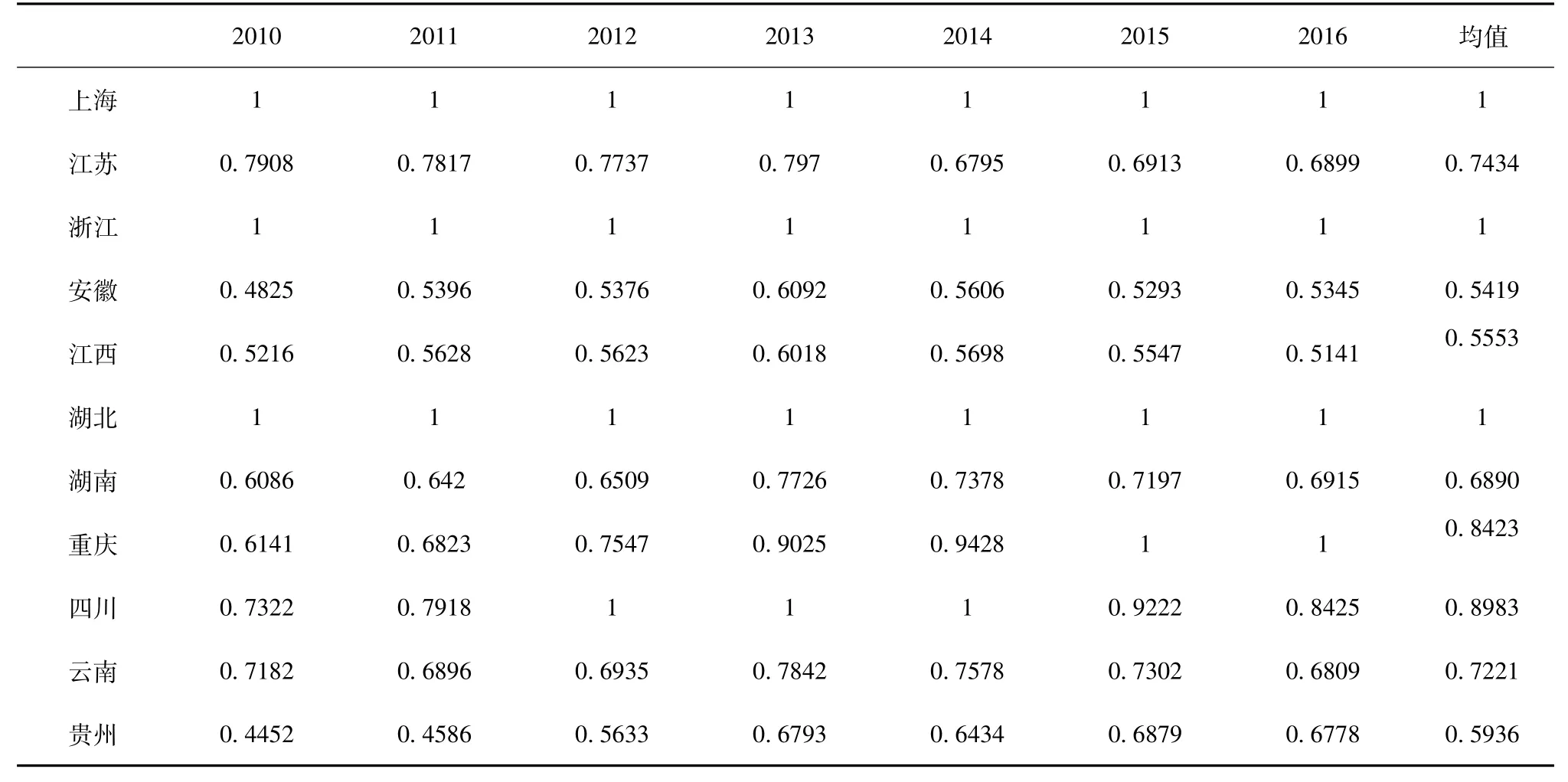
表2 长江经济带工业用水效率测算结果

表3 长江经济带各区域工业用水效率均值

从长江经济带11省市来看，上海、浙江、湖北的效率值最高，每年均达到了有效；其次是四川、重庆，分别有两年和三年达到了有效；而江西、安徽的工业用水效率一直处于较低水平，需要借鉴效率高的省市的节水技术及管理方式，尽快提高工业水资源利用效率。

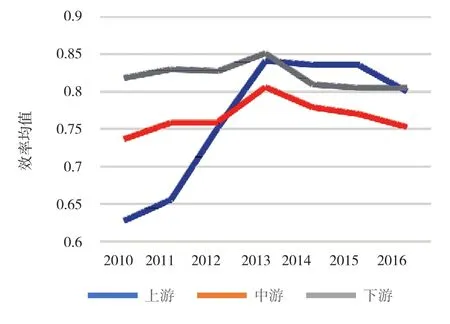
图1 长江经济带区域工业用水效率值变化

图2 长江经济带各省市工业用水效率

3.1.2 bootstrap-DEA法调整结果

采用MaxDEAPro7.6软件对非期望产出SBM模型测出的效率值进行修正，修正结果见表4，由于篇幅原因这里就不列出其在95%显著水平下的置信区间。

表4 2010-2016年长江经济带工业用水效率bootstrap-DEA法调整结果

对比表2与表4的结果可以发现，剔除随机因素干扰后的效率值普遍有所下降，说明长江经济带大部分地区受随机因素干扰是显著的。调整后的2010-2016年长江经济带工业用水效率均值为0.5915，效率值有很大的提升空间。修正前后的呈现出的变化趋势基本一致，经bootstrap-DEA法调整后的效率值更接近工业用水的真实效率值。

从图3可以看出，2010-2016年长江经济带各区域工业用水效率均值均在下降，调整后的下游地区效率均值最高，其次是上游地区，最后是中游地区。从图4还可以看到，调整后的效率均值除湖北为1外，其他地区的工业用水效率均值都小于1，故可以对长江经济带11省市的工业用水效率进行完全排序，从高到低依次为湖北、浙江、上海、四川、重庆、云南、江苏、湖南、安徽、贵州、江西。

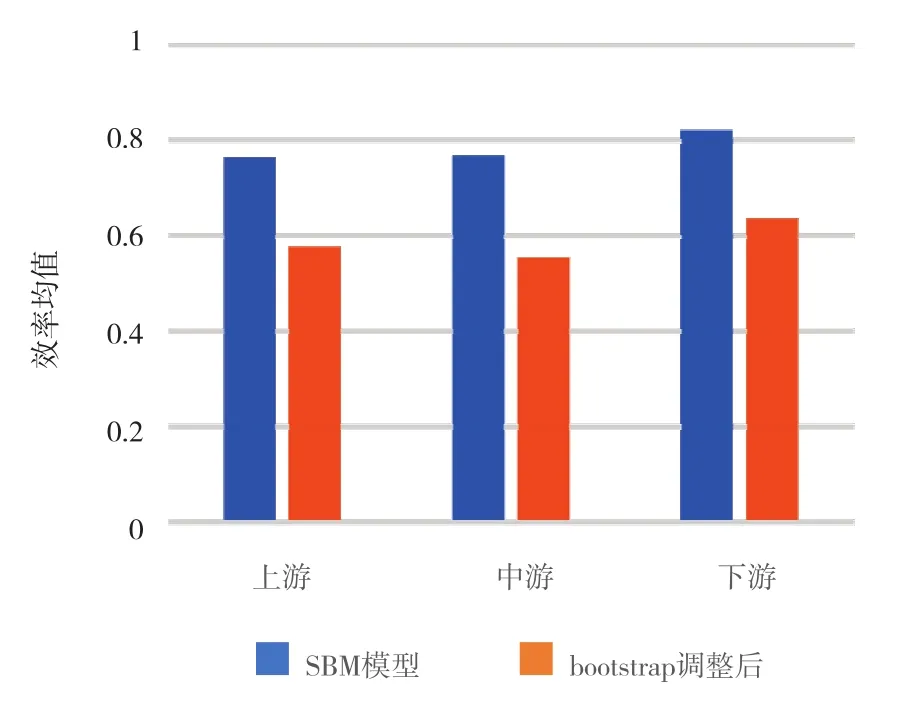
图3 长江经济带各区域调整前后工业用水效率均值对比图

图4 长江经济带各省市调整前后工业用水效率均值对比图

3.2 长江经济带工业用水效率动态分析

由表5可以看到，2010-2016年长江经济带工业用水ML指数均大于1，说明长江经济带工业用水效率每年都一定程度的提升，其中2015-2016的提升程度最大，达到了27个百分点；从ML指数的分解情况来看，工业用水效率提高来源于技术效率的提高及技术进步，更多的得益于技术进步。2010-2011年的技术效率下降了3.4个百分点，其工业用水效率值提升全靠技术进步了40.5个百分点。

表5 长江经济带工业用水ML指数及分解值

4 结束语

本文在考虑环境因素的基础上，将工业废水中的化学需氧量排放量作为非期望产出指标加入指标体系，采用基于非期望产出的SBM-DEA模型对2010-2016年的长江经济带工业用水效率进行了静态测算，并考虑到随机冲击的影响，使用bootstrap法对效率值进行纠偏处理，得到以下结论：修正后的效率值普遍有所下降，说明随机冲击的影响不容忽视；从长江经济带整体工业用水效率来看，长江经济带整体工业用水效率不高，呈现出先增大后减少的趋势，存在着较大的提升空间。从长江经济带三大区域来看，长江经济带各区域的工业用水效率值差距较大，长江经济带下游工业用水效率值最高，其次是上游，最后是中游；从长江经济带各省市工业用水效率来看，各省市效率值从高到底依次为：湖北、浙江、上海、四川、重庆、云南、江苏、湖南、安徽、贵州、江西。再用Malmquist-Luenberger指数从动态角度进行测算，得出2010-2016年长江经济带工业用水效率值每年都有所增长，其效率值的增长得益于技术进步。综合以上研究，结合长江经济带实际情况，提出以下建议：优化工业结构，优化工业布局。合理优化工业结构，尽量将高耗水、高污染的重化工业向轻污染、节水型的工业产业转型，不断减少高耗水、高污染的重化工产业所占比重，大力推进高新产业的发展，促进产业结构优化升级。引进国外先进的节水设备及技术，加大工业节水技术研究经费投入，加快对长江经济带高耗水工业行业如火力发电、钢铁的技术改造。鼓励企业进行自主创新，研发工业生产及节水技术，进一步提高工业水资源利用效率。