考虑结合面影响的拉杆组合转子动力学特性分析
2020-07-13葛玉梅
李 鑫,杨 洋,葛玉梅
(西南交通大学力学与工程学院,成都 610031)
引言
轮盘式周向拉杆组合转子因其装配、检修方便等特点[1]而广泛应用于重型燃气轮机转子系统中。其主要通过拉杆螺栓将各级轮盘固定而成一个整体,轮盘之间的接触刚度对整个系统的动力学特性影响较大。早期的研究表明,人们主要将拉杆组合转子视为一个整体进行研究,通过有限元手段、离散质量法以及传递矩阵法来分析转子系统动力学特性,但这样的处理会使其固有频率高于实验观察的结果[2]。因此,建立更加精确的拉杆组合转子系统动力学模型是必要的。汪光明等[3]针对鼓筒式拉杆转子模型,对轮盘连接界面采用铰链-等效弹簧的处理形式,求出系统的解析解,但该模型并未给出等效弹簧刚度值的计算方法。饶柱石等[4]在G-W接触模型的基础上,在考虑轮廓表面波纹度的影响,推导出弹性接触状态下的接触刚度的计算公式,弥补了汪光明提出的铰链-等效弹簧模型的不足。文献[5-8]均采用铰链-等效弹簧的方法建立拉杆组合转子模型。其中,文献[5]建立了考虑轴承非线性油膜力的12个自由度的轴向拉杆组合转子模型,采用非线性弯曲弹簧处理轮盘之间的接触,通过分析组合转子非线性行为,并与整体式转子系统比较,发现组合转子更具稳定性。文献[7-8]将转静子定点碰磨加入到考虑非线性油膜力的拉杆组合转子轴承系统,研究了系统的动力学特性。研究表明随着转速的变化,系统在非线性油膜力和碰磨力的作用下会有明显的非线性特性。此外也有采用刚度修正法[9-10]、薄层单元法[11]、有限元法[12]等效拉杆组合转子轮盘结合面刚度。
综上所述,在分析拉杆组合转子动力学特性时,建立一个合理的且能够反应系统实际情况的模型具有重要意义。而在考虑拉杆组合转子轮盘结合面之间的接触刚度时,以往的学者多采用Herzt接触模型或者GW接触模型来推导接触刚度,与分形接触理论比起来并不能很好反映真实接触情况。其次,在建立拉杆组合转子模型时,多采用对称结构,并没有考虑到因轮盘的存在而出现的结构不对称。
本文将拉杆组合转子轮盘进行简化,建立考虑轮盘接触的转子模型,使其更加贴近拉杆组合转子系统实际结构。其次基于分形理论推导拉杆组合转子轮盘之间的弯曲接触刚度,并考虑拉杆因横向振动而产生弯曲对接触刚度的影响,进而采用铰链-等效弹簧来模拟轮盘结合面。最后用数值仿真分析考虑轮盘之间的接触刚度对系统的动力学特性影响。
1 拉杆组合转子模型简化
研究表明,组合轮盘的使用是为了提高转子系统的刚度,增大其固有频率。但由于轮盘带有质量,又使得系统固有频率降低。从计算和实验数据来看,二者作用可相互抵消[3]。
图1为一杆组合转子的实验模型[3],由8根拉杆将8个轮盘连接的滚动轴承支撑的周向拉杆组合转子。对其进行简化:将带有叶片的轮盘简化为具有质量的刚性薄圆盘。在考虑轮盘之间的接触时,为了简化计算,只考虑两个轮盘之间的接触(即将轮盘分为两组,各组之间的轮盘整合为一个整体,只考虑整合后的轮盘之间的接触特性),从而建立考虑结构非对称的简化模型如图2所示。考虑到结构的不对称,左右两组各有3个和5个轮盘。
该模型共有5个单元,共4个节点,16个自由度。其中单元分别有转轴1-2梁单元、2-4梁单元,轮盘组OA、OB构成的盘单元以及考虑轮盘接触的梁单元2-3。其中梁单元2-3是由左、右轮盘组各提供的一个轮盘和轮盘间的粗糙接触层共同组成。
对于实际的拉杆组合转子系统而言,由于制造技术及装配工艺的限制,轮盘的质心往往与其几何形心不重合,会使得转子系统受到不平衡质量激励力。因此,定义轮盘组OA处存在质量偏心,将偏心质量考虑到模型中。
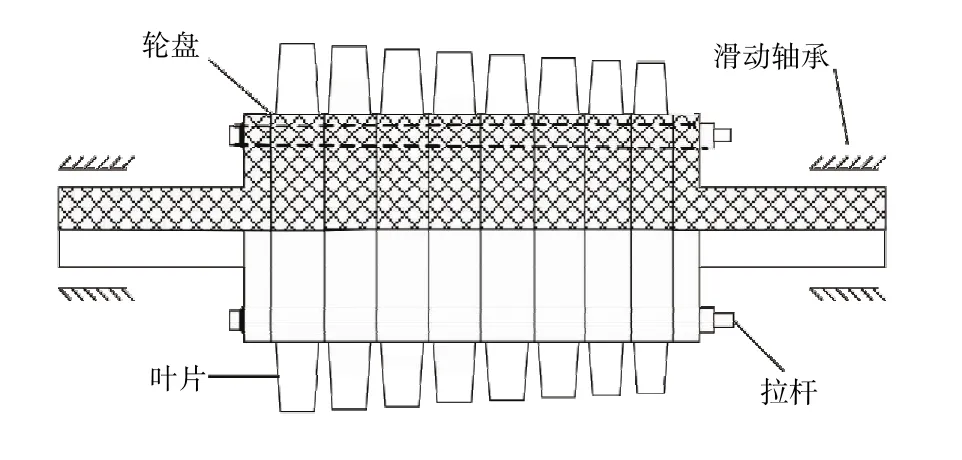
图1 拉杆组合转子实验模型
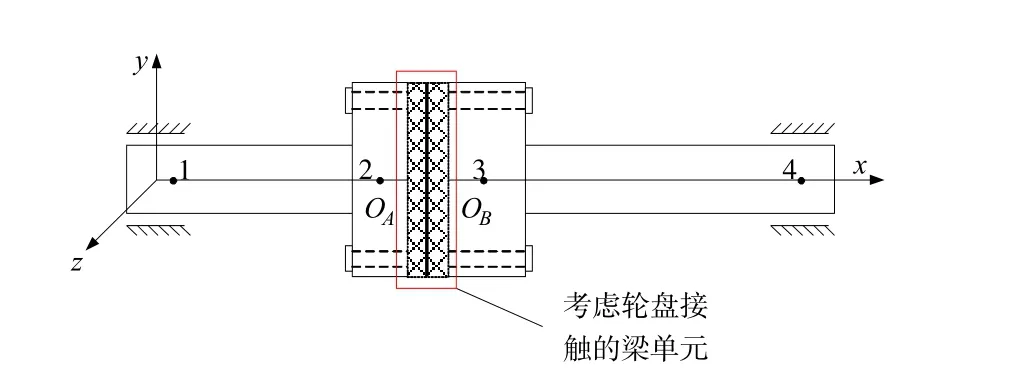
图2 拉杆组合转子简化模型
2 拉杆组合转子轴承系统动力学模型建立
2.1 结合面接触的弯曲刚度
研究表明[13],很多加工过的零件表面可以观察到自仿射和多尺度的分形特征。因此在研究粗糙结合面的接触刚度时,可以采用分形的思想。
假设在结合面的接触过程中只发生弹性变形,可得到其接触力的表达式[14]:
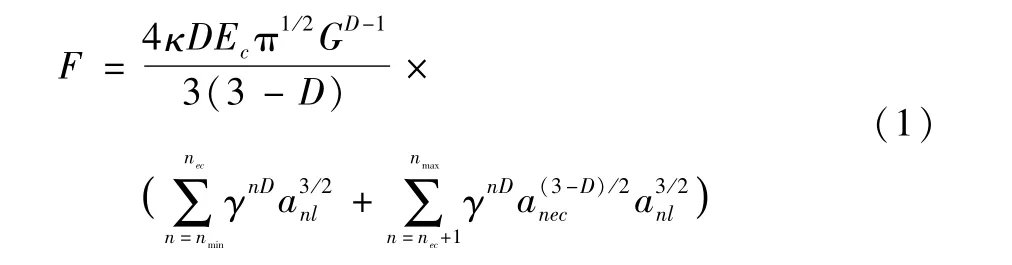
其中,D为分形维数,G为轮廓特征参数,κ为一系数,反映各等级微凸体面积分布概率的关系,Ec为材料弹性模量,anl为尺度序数为n的微凸体的接触面积,anec为发生弹性变形的临界接触面积,n为尺度序数,nmin和nmax分别表示最大和最小尺度序数。
各尺度序数下的接触面积与接触距离的关系为:

其中,Rn为该尺度序数下的曲率半径,wn为接触距离。
联立式(1)和式(2),将接触力对接触距离求导便得到结合面的法相接触刚度,其表达式为:

因此,结合面的弯曲刚度可以表示为:

其中,,为等效分布弹簧的弹性常数,Ar表示真实r接触面积,Ia表示接触面名义截面矩,ηra是真实接触面积与名义接触面积之比,定义为ηra=。
根据文献[15]可得切向接触刚度:

其中,v为材料泊松比。
拉杆组合转子在发生横向振动时,将导致拉杆轴线发生弯曲,从而使得此时的拉杆在原有预紧力伸长量的基础上会产生一定的伸长或缩短。因此,拉杆内部会产生一个抵抗弯曲变形的力矩,这等于给系统附加了抵抗因横向振动而产生弯曲变形的抗弯弯矩。
当拉杆受到F0的预紧力作用时,可得到单根拉杆的变形量:

其中,Er为拉杆的弹性模量;Lr和Δl分别为拉杆的原长和形变量;r0为拉杆的半径。
图2可以看出,8根拉杆均匀周向分布在轮盘上,当转子发生横向振动时,处在不同位置的拉杆距离偏转中性面(偏转过程中伸长率为0的面)的距离不同。因此设Riy表示第i根长拉杆距离偏转中性面的距离。当轮盘偏转时,任意一根拉杆都会伸长或缩短,如图3所示。
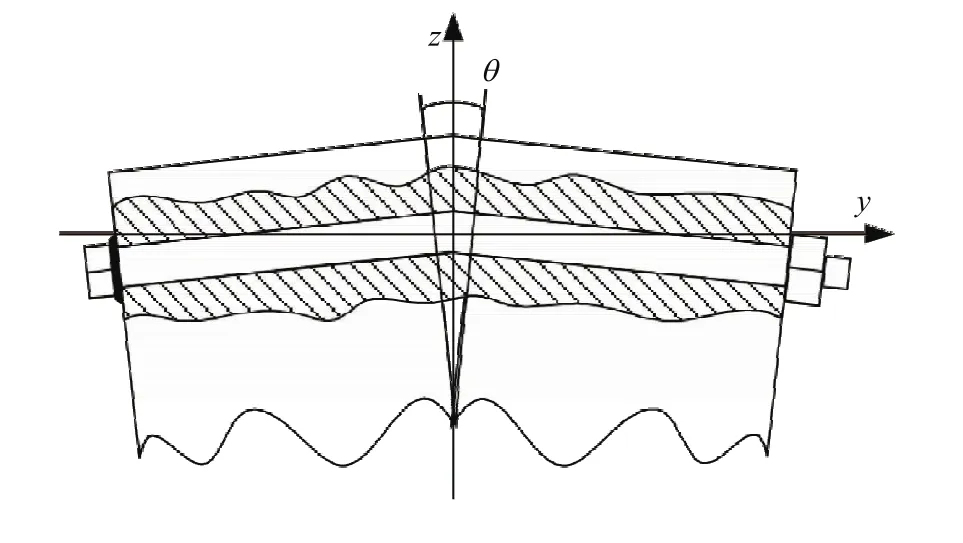
图3 存在倾角的转子轴段模型
就转子轴段中的某一个拉杆而言,在预紧力和弯矩作用下总的产生的形变量为:

其中,Riy表示拉杆因轮盘偏转产生的距离。进而可得到此时拉杆所受预紧力以及拉杆作用到轮盘上的弯矩:

当有n根拉杆共同作用时,轮盘上总的拉杆预紧力为∑Mi,则因拉杆产生的总的弯曲刚度为:
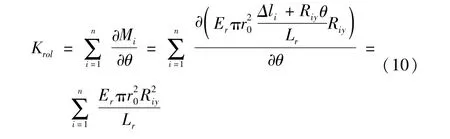
结合2.1节前面所推导的轮盘结合面接触弯曲刚度KG,二者是并联关系,故在轮盘接触层上的总的弯曲刚度:

2.2 动力学方程的构建
本文采用Timoshenko梁-轴理论建立转轴单元以及考虑轮盘接触的梁单元模型,采用盘单元模拟轮盘组。
2.2.1 转轴单元的运动方程
根据Timoshenko梁-轴理论建立转轴单元运动微分方程为:
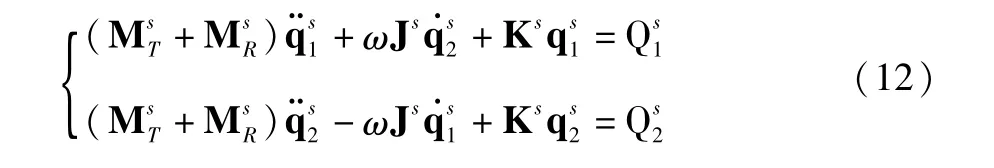
其中,q1、q2分别表示转轴在xy和xz平面内的平动和转动自由度分别为单元质量矩阵和单元质量惯性矩阵,Js为单元陀螺矩阵,Ks为单元刚度矩阵,为单元节点处所受到的广义外力,ω为角速度。
2.2.2 考虑轮盘接触的梁单元的运动方程
为了考虑拉杆组合转子轮盘之间的接触,由接触面及其左右各一个轮盘组成新的梁单元,并将其命名为考虑轮盘接触的梁单元。为了将轮盘接触的法向接触刚度和切向接触刚度运用到考虑轮盘接触的梁单元中,将粗糙接触层作为一个仅具有刚度的Timoshenko梁单元,故对于本文中的考虑接触的轮盘梁单元2-3来说,其单元刚度由左右各一个轮盘刚度和粗糙接触层刚度串联而成。由Timoshenko梁理论可知,单元的刚度矩阵(由于对称,仅考虑xy平面)可表示为:
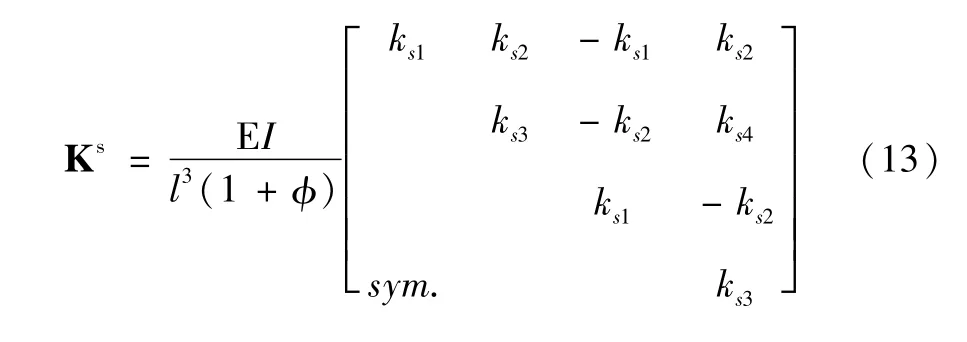
其中各参数可表示为:ks1=12,ks2=6l,ks3=l2(4+为单元材料弹性模为泊松比;μ为截面剪切系数[16],其值由截面几何形状决定,一般在0.45(0.9之间,对于薄壁圆截面μ=0.5,实心圆截面μ=0.9,I为截面惯性矩,l为单元长度,A为单元截面面积。
由式(13)可知,组成刚度矩阵的参数主要由ks1、ks2、ks3和ks4四个变量组成。由Timoshenko梁单元刚度矩阵的定义,可知每个参数的物理意义可表示为:当考虑图2的xy平面内的单元2-3时,参数ks1、ks4表示当同时约束节点3的所有自由度,在节点2处施加剪力Fy2,求得节点2处的位移y2和节点3处的弯矩My3,从而得出同理约束节点3的所有自由度,同时约束节点2的平动自由度,在节点2处施加弯矩My2,求出节点2处的转角Qy2和节点3出的弯矩My3,从而得出
根据各参数的物理意义可以发现,ks1等于粗糙结合面的剪切刚度KT,ks3等于粗糙结合面的等效弯曲刚度KC。由于粗糙结合面接触层很薄,在求ks4时,可认为My3与施加的My2等值反向,故ks4等于粗糙结合面的等效弯曲刚度的负值,即等于-KC。对于“短粗”的Timoshenko梁,采用数值仿真,取单元半径为0.03 m,单元长度0.015 m,弹性模量为210 GPa,泊松比为0.3,密度为7800 kg/m3。当长度L增加一倍时,其参数ks2可视为不变,其余参数ks1、ks3和ks4可通过串联得到,如图4所示。
由此,根据串联关系便可得到考虑接触的轮盘梁单元的刚度矩阵。进而可得到考虑轮盘接触的梁单元运动方程:

图4 不同单元长度的Timoshenko梁单元刚度矩阵(图a中单元长为l,图b中单元长为2 l)
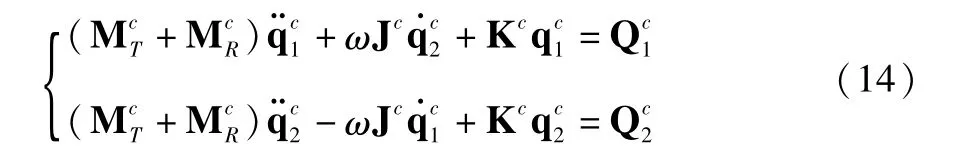
其中,q1、q2分别表示单元在xy和xz平面内的平动和转动自由度分别为单元质量矩阵和单元质量惯性矩阵,Jc为单元陀螺矩阵,Kc为单元刚度矩阵,为单元节点处所受到的广义外力,应包括单元的力和力矩;ω为角速度。
2.2.3 盘单元的运动方程
轮盘组OA、OB采用盘单元,其运动微分方程为:

2.2.4 轴承控制方程
此处采用滚珠轴承[17],在忽略润滑油的影响下轴承的运动微分方程可写作如下形式:

其中,qb=[yi,zi],i=1,4表示轴承处y、z方向位移,Cb为轴承阻尼矩阵,Kb为滚动轴承的刚度矩阵,Qb为轴承处的支反力。
组装各个单元,构建拉杆组合转子的运动方程为:
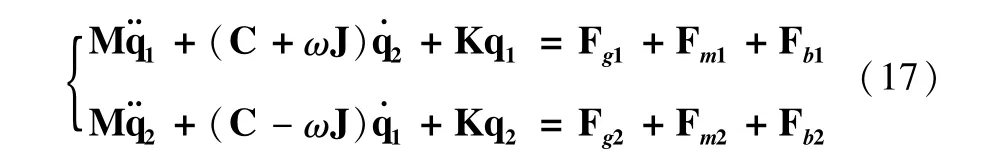
其中,M、C、J、K分别为总质量阵、总阻尼矩阵、总陀螺矩阵和总刚度矩阵,Fg、Fm、和Fb系统受到的重力、不平衡激励力和轴承力,ω为系统转速。
采用图2所示的拉杆组合转子简化实验模型求解系统动力学特性,转子模型的各个物理参数见表1。
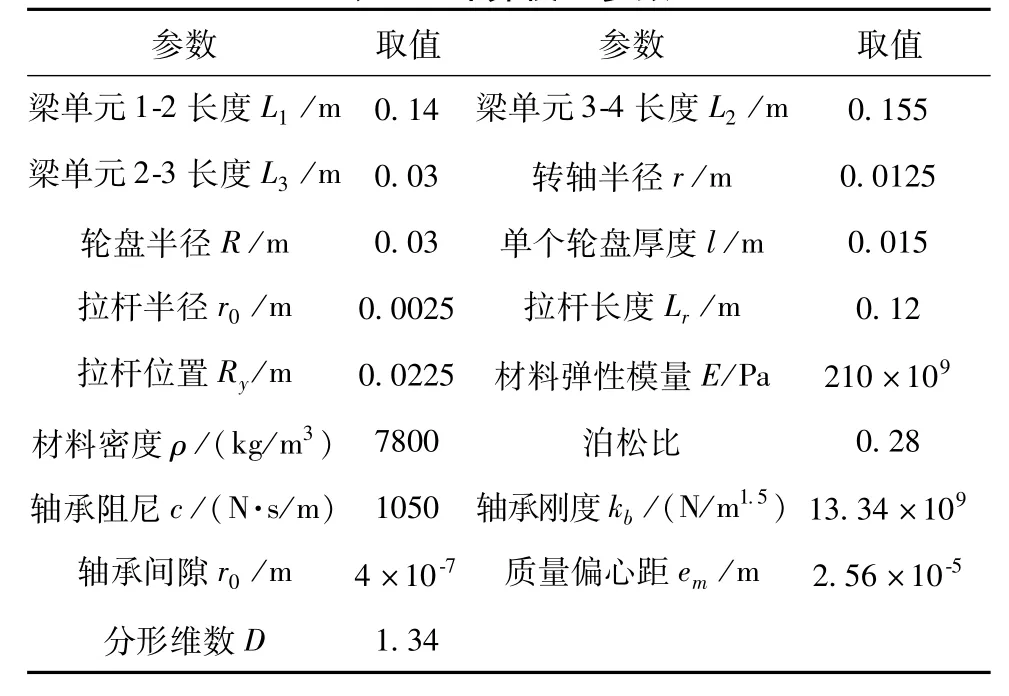
表1 计算模型参数
3 系统动力学特性分析
本节采用四阶Runge-Kutta法对已建立的系统动力学方程进行求解。在分析考虑轮盘接触刚度对拉杆组合转子系统的影响时,考虑轮盘组OA处的质量偏心,其偏心距为em。绘制出轴承1处y方向位移随转速的变化如图5所示。

图5 轴承1处y方向的位移随转速的变化图(偏心距em=0.0256 mm)
如图5所示,描绘了在考虑接触以及将轮盘结合面视为一个整体的情况下,轴承1处的振动幅值随系统转速的变化情况。可以发现,当系统处在非共振区域时,考不考虑轮盘之间的接触对y方向位移幅值影响不大。这是由于转子系统在非共振频率下运行时,系统的整体横向位移较小,拉杆螺栓提供的拉力足以使各级轮盘在工作中保持紧密贴合,此时考不考虑轮盘接触刚度对系统振动响应影响不大。
当系统处在共振区域,考虑轮盘之间的接触后会使得共振位移幅值减小,共振频率也有一定的减小,即从1493 rad/s降低到1482 rad/s。这是由于当考虑轮盘接触时,转子轮盘接触部位不再视为整体结构,因此会降低系统的整体刚度,而此时系统其他参数是没有发生改变的,故系统固有频率会减小。
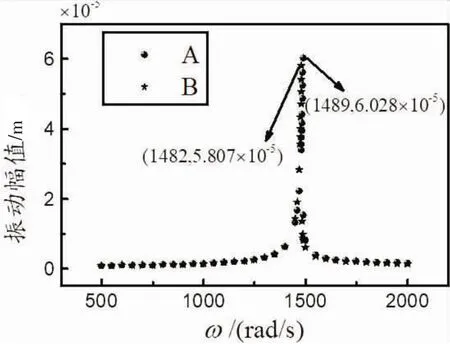
图6 不同轮盘接触刚度下轴承1处y方向的位移随转速的变化图(偏心距em=0.0256 mm)
图6反映了不同轮盘接触刚度下,轴承1处的振动幅值随系统转速的变化情况。其中图例A表示接触刚度较大的情况,图例B表示接触刚度较小时。从图5和图6可以看出,当轮盘接触刚度越大时,系统的共振频率越接近整体式转子系统。这是因为随着轮盘接触刚度的增大,使得整体系统刚度增大。由此可以看出,当拉杆组合转子在由螺栓预紧时,当拉杆螺栓提供的拉力足够大时,此时轮盘结合面的接触刚度足够大,此时的系统可等效为整体式转子。
图7给出了不同转速下轴承1处的时间历程图和轴心轨迹图。其中黑色线条表示考虑轮盘之间的接触刚度,红色线条表示不考虑轮盘之间的接触。
从图7可以看出,当系统工作转速远低于系统共振频率1493 rad/s(不考虑接触)或1482 rad/s(考虑接触)时,此时系统的振动响应都比较小,此时接触刚度对系统的振动响应影响不大,因此考不考虑轮盘之间的接触对系统响应影响不大。随着转速的提高并逐渐逼近共振频率,系统的振动逐渐加剧,尤其工作频率在共振区域时,振动响应增加更为明显。观察二者轴心轨迹图可以发现其均近似为一个圆,由于共振引起的响应增大,所以导致轴心轨迹的圆随着转速的增大而变化。
4 结论
对于通过拉杆螺栓而连接在一起的拉杆组合转子而言,与整体式转子不同,其轮盘接触的刚度对转子系统影响是不可忽略的。通过建立拉杆组合转子模型,并采用数值分析的方法研究了轮盘接触刚度对系统动力学特性的影响,得出以下结论:
(1)相比于将拉杆组合转子轮盘接触部位视为一个整体来看,考虑轮盘接触后,转子系统整体刚度会降低,当接触刚度随着螺栓预紧力的增大而增大至一定值时,系统可视为整体式转子。因此,在建立拉杆组合转子系统计算模型时,一般需要考虑各级轮盘之间的接触的影响。
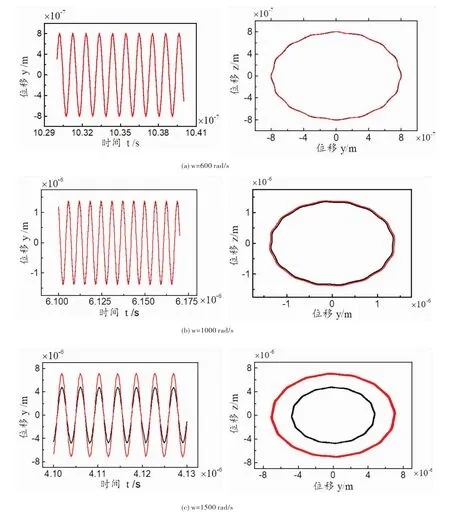
图7 不同转速下轴承1处的时间历程图和轴心轨迹图(偏心距em=0.0256 mm)
(2)考虑轮盘接触时,会使得系统共振区域的幅值变小,同时降低了共振频率。对于非共振区域影响几乎不变。
