基于Excel的均相热力学性质计算

吕和坤，郭丹，赵龙涛，董雪茹

(河南工程学院 材料与化学工程学院，河南 郑州 450000)

化工热力学是化学工程与工艺学科的一个核心课程，是必修的专业基础课程，以高等数学、物理化学等课程为基础，为分离工程、反应工程和化工设计等化学工程其他学科的学习提供重要的概念、模型、基础数据和计算方法，是化工专业学生学习的核心环节之一，具有重要的地位[1].

在化工热力学教学中，概念难以理解、公式复杂难懂、大部分计算均需较为复杂的试差或者迭代等都是学生学习时遇到的问题.其中，概念与公式的问题均可通过讲解的方式解决，复杂计算则难于在课堂上讲述清楚，是授课的难点[2].现在，解决实际物系热力学性质计算主要依靠计算机辅助.涌现出了很多新软件.Aspen Plus、Chem CAD、ProⅡ等化工通用模拟软件包含了许多组分的基本物性参数，有丰富的状态方程和活度系数方程，在化工模拟计算中展现出了强大的优势，但是这类软件不能详细地展示计算过程，不利于学生对计算过程原理和方法进行掌握.采用C语言，Matlab等进行编程同样可以解决复杂的热力学计算，但需要学生对编程语言较为熟悉，具有较高的计算机应用水平.Excel 是微软办公套装软件的一个重要组成部分，可以进行各种数据的处理、统计分析，广泛地应用于管理、统计、化工计算等众多领域.Excel具有强大的运算功能，其图表及数值处理功能十分强大，用户无需编程，可进行多项式拟合、非线性单变量求解、多变量规划求解等复杂计算，计算过程简单明了，不易出错，教学举例中具有很好的适用性.

均相热力学性质的计算是化工过程计算的基础之一，在实验研究和化工设计中具有重要作用.其中会用到各种状态方程，其中，立方型方程因其型式简洁、易于理解等优点，经常用于流体热力学性质计算的教学中.在常用的立方型方程中，PR方程是在RK方程基础上发展而来的，有比RK方程更好的计算精度，应用较为广泛.本文就用PR方程以Excel在均相热力学性质计算方面用实例进行简要说明.

1 Excel在均相热力学性质计算示例

我们要用PR方程计算402 K、2 MPa下，摩尔分数分别为0.2和0.8的异丁烷和正丁烷混合物的摩尔体积、压缩因子、偏离熵、偏离焓与逸度，所用公式有[3]：

(1)状态方程，状态方程有很多种，常见的为立方型方程和多参数方程，本文以PR方程为例.

其中：

(2)混合法则，PR方程的混合法则如下，

其中kij为相互作用参数.

(3)偏离函数，最常用的偏离函数为偏离焓与偏离熵：

(4)压缩因子

(5)逸度系数(包括组分的逸度系数)

①在Excel表格的单元格内，依次填入温度T、压力P、异丁烷和正丁烷的临界温度Tc、临界压力Pc、偏心因子Ω、摩尔分数x、相互作用参数kij(本例均假定为0)与气体通用常数R.

②计算PR方程的参数ai和bi，两式分别以Excel要求的形式：

“=0.457235*(8.314*B5)^2/B6*(1+(0.37646+1.54226*B7-0.26992*B7*B7)*(1-(B3/B5)^0.5))^2”

“=0.077796*8.314*B5/B6”

“=0.457235*(8.314*C5)^2/C6*(1+(0.37646+1.54226*C7-0.26992*C7*C7)*(1-(B3/C5)^0.5))^2”

“=0.077796*8.314*C5/C6”

填入B10、B11和C10、C11单元格.

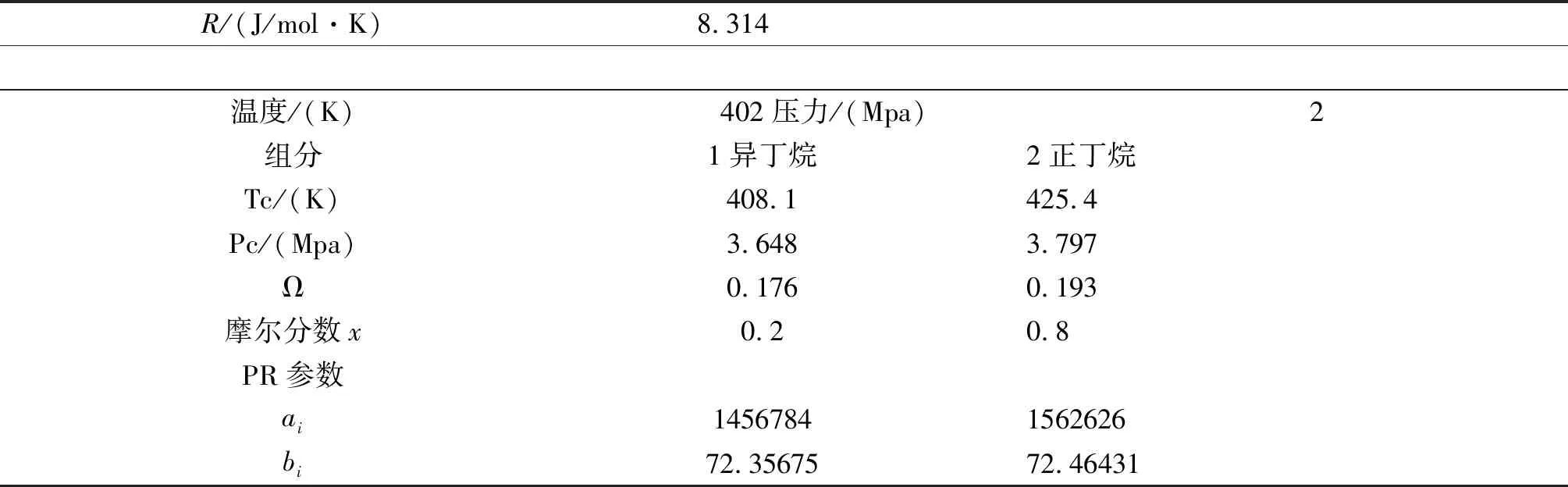
R/(J/mol·K)8.314温度/(K) 402压力/(Mpa) 2组分1异丁烷2正丁烷Tc/(K)408.1425.4Pc/(Mpa)3.6483.797Ω0.1760.193摩尔分数x0.20.8PR参数ai14567841562626bi72.3567572.46431

③类似的，计算出混合物的PR方程参数a，b.

aij1211456784150877721508777156262617混合物性质18a154116119b72.4428

④摩尔体积V的计算.我们采用软件自带的单变量求解来解决这个问题.采用单变量求解，需要设定自变量和函数的目标值.我们将PR方程改写成：

将P、T、R及a、b的值列于B22到B26，在D22输入迭代初始值，D23输入f(V)的表达式，“=B22-B24*B23/(D22-B26)+B25/(D22*(D22+B26)+B26*(D22-B26))”，然后点“单变量求解”，设置目标单元格D23，目标值为0，可变单元格为D22.即可求出摩尔体积.

22P2V1205.523T402f(V)0.0024R8.31425a154116126b72.4428

⑤同样，将偏离函数、压缩因子、逸度系数等公式正确带入，均可正确计算.此处不再赘述.

28Z0.72137529lnϕ-0.25163031lnφi1232-0.23168-0.25665

2 结 语

流体热力学性质计算是很复杂而又很重要的，此部分的教学往往枯燥无味，学生难以掌握.同时由于例题与习题都很繁杂、费时，大多数题目学生很少动手计算，从而掌握的不扎实.现有的一些辅助计算软件看不到具体的计算过程，只有输入条件和输出结果，不利于学生的学习.采用Excel进行计算的话，更加透明，可反映出计算原理与过程，对知识的掌握也会更加牢固.