梁拱组合连续刚构桥极限承载力影响因素
2020-07-13廖超
廖超
核工业西南勘察设计研究院有限公司,四川成都 610011
0 引言
空腹式连续刚构桥是将常规连续刚构桥箱梁根部腹板挖空而形成,空腹面积较小,空腹节段较短,其截面受力为梁结构受力[1-3]。梁拱组合刚构桥结合常规连续刚构桥和空腹式连续刚构桥2种桥型的优势,进一步增加空腹节段的长度和面积,主墩根部箱梁截面分为上下两肢,上弦主梁趋于梁结构受力,下弦主梁趋于拱结构受力,以受压为主。下弦主梁受上弦主梁影响,分担部分弯矩,属于压弯受力杆件,受力较为复杂[4-7]。该桥型形式简单,结构轻盈,不但兼具拱桥和梁桥的优点,而且有望克服常规连续刚构桥的下挠和开裂问题,同时减轻空腹段以外箱梁的受力,增强桥梁的跨越能力。
桥梁结构极限承载力是指桥梁结构失效前承受外荷载的最大能力。最初采用强度设计准则评判材料是否屈服,即仅以构件材料最大应力乘以安全系数来评判材料是否屈服。但强度设计准则中构件的某一个截面开始出现屈服并不代表整个结构完全发生破坏,结构还剩余一定的富裕强度,因此提出极限荷载的概念[8-11]。
求解桥梁结构极限承载力的传统方法主要是线弹性分析方法,其中线弹性屈曲法最具代表性,但该方法没有考虑结构非线性因素对桥梁结构极限承载力的影响,仅适用于比较理想的结构,适用范围较小[12-15]。随着计算机技术被引入到桥梁的设计分析中,求解桥梁结构的极限承载力时可以考虑诸多非线性因素的影响。非线性静力弹塑性分析方法的优势明显,该方法能够同时考虑几何非线性因素和材料非线性因素对结构极限承载力的影响[16-18]。
影响大跨径梁拱组合连续刚构桥极限承载力的设计因素较多,这些因素决定了大跨径梁拱组合连续刚构桥的承载能力[19-25]。因此,分析研究混凝土强度、边中跨比、截面空腹率、上下弦梁刚度比等设计因素对大跨径梁拱组合连续刚构桥极限承载力的影响,准确知道其破坏形式及破坏特点,对保证施工安全,提高梁拱组合刚构桥的极限承载力,具有一定的理论意义及实用价值。
1 工程背景
礼嘉嘉陵江大桥箱梁如图1所示(图中单位为cm),采用三向预应力结构,单箱单室截面,道路中心内侧悬臂翼缘宽4.45 m,外侧悬臂翼缘宽4.40 m,箱梁顶板宽17.85 m,底板宽为9.00 m,箱梁顶板厚度除0号块局部加厚至0.62 m,其余段均为0.32 m。

图1 礼嘉嘉陵江大桥主墩悬臂梁分段布置图
上弦杆箱梁悬臂根部梁高6.5 m(以梁体中心线为准)。梁高纵向范围为桥墩中心线东西侧各4.5 m,共9.0 m。此范围以外,梁高由6.5 m线性过渡到跨中梁高5.0 m(终点为9、9′和9″剖面),9、9′和9″剖面至11、11′和11″剖面为跨中梁高5.0 m等高段范围,再由梁高5.0 m线性过渡到梁高5.483 3 m,与下弦汇合。箱梁腹板厚度从三角区域到根部区域由0.8 m逐步过渡为1.2 m,在 2P3─2P4、2P3′─2P4′、3P3─3P4、3P3′─3P4′节段内完成变化;箱梁腹板厚度从三角区域到合拢段区域逐步由0.8 m过渡到0.5 m,在2P16、2P16′、3P16、3P16′节段内完成变化。下弦杆底缘线按2.2次抛物线规律变化,坐标原点为下弦底缘线延伸线与桥墩边缘的交点,变化方程为:
y=-0.000 692 4(119-x)2.2+25.5,
式中:x为下弦杆底缘线上某点与原点的水平距离,y为其与原点的竖直距离。
下弦杆跨中顶板、底板及腹板厚度均为0.6 m,顶底板宽9.0 m,梁高4.8 m。从下弦杆与上弦杆的交汇处到下弦杆与桥墩交汇处的顶板、底板及腹板厚度分别由0.6 m增大至0.8 m。
桥墩P2、P3均为独柱墩,横桥向分左右两幅,左右幅桥墩横桥向中心距为20 m。墩顶与主桥主梁固结,墩底接承台和群桩基础。
工程主桥采用双幅形式,标准断面单幅宽18.05 m,按照单幅四车道,双向八车道设计,内侧设置2个宽3.50 m的小车道,外侧设置2个宽3.75 m的大车道,考虑现实需要,两侧外边缘各加设1条宽度为2.0 m小道,便于后期检修及行人过江。即单幅布置为2.0 m(检修兼人行道)+15.5 m(机动车道)+0.55 m(防撞护栏)=18.05 m,两幅之间设1.9 m中央分离带。
2 结构有限元模型分析
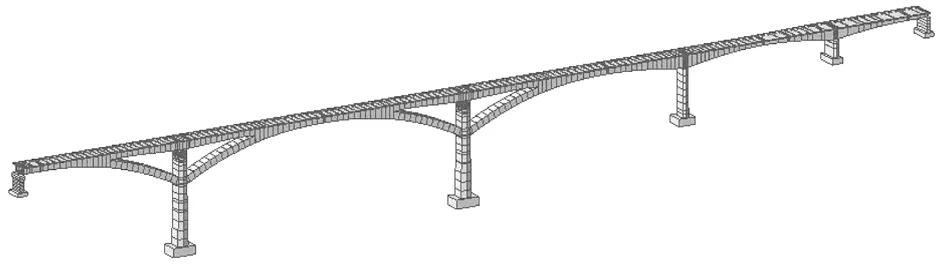
图2 礼嘉嘉陵江大桥成桥状态有限元计算模型
为研究桥梁结构极限承载力及其影响因素,利用有限元软件Midas Civil建立礼嘉嘉陵江大桥的分析模型,如图2所示。除施工过程中的临时扣背索采用只受拉桁架单元模拟外,其余构件均用梁单元进行模拟。边界模拟中墩底采用固结形式,墩梁固结处采用刚性连接。成桥阶段共有334个梁单元,381个节点。
3 结构极限承载力的影响因素
3.1 主要材料及性能
礼嘉嘉陵江大桥工程所用混凝土、预应力钢绞线和普通钢筋的力学性能如表1~3所示。

表1 混凝土力学性能指标

表2 预应力钢绞线力学性能及计算参数
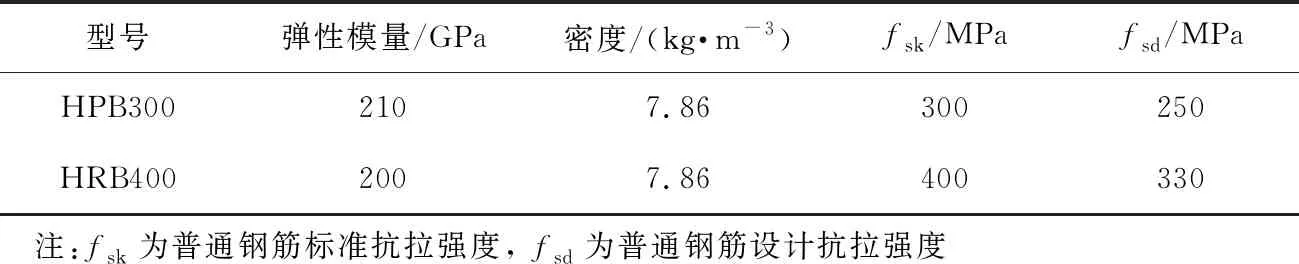
表3 普通钢筋力学性能及计算参数
3.2 混凝土强度
礼嘉嘉陵江大桥主墩和主梁分别采用C50和C60混凝土,为研究不同混凝土强度对结构极限承载力的影响,考虑主墩和主梁分别采用C45、C50、C55、C60四种标号的混凝土,分析计算成桥运营阶段的结构极限荷载系数。
3.2.1 主墩
通过同时考虑几何非线性及材料非线性的双重非线性分析,得到不同混凝土强度等级对应的主墩结构控制点的荷载-位移曲线,如图3所示。

图3 主墩不同混凝土标号对应控制点的稳定安全系数-位移曲线
通过计入几何及材料双重非线性因素的非线性静力弹塑性分析,得到主墩不同混凝土强度等级下结构极限荷载系数,C45、C50、C55、C60混凝土主墩的极限荷载系数分别为8.80、8.85、8.87、>8.92。
由图3可以得出:主墩采用4种混凝土强度等级进行模拟分析得到的结构极限荷载系数比较接近,混凝土标号C45、C50、C55分别比标号C60的结构极限荷载系数分别减少1.35%、0.78%和0.56%,说明混凝土强度等级对主墩的结构极限承载能力影响较小。随着混凝土强度的增大,极限荷载系数略有增加。
3.2.2 主梁
通过同时考虑几何非线性及材料非线性的双重非线性分析,得到不同混凝土强度等级对应的主梁结构控制点的荷载-位移曲线,如图4所示。

图4 主梁不同混凝土标号对应控制点的稳定安全系数-位移曲线
通过计入几何及材料双重非线性因素的非线性静力弹塑性分析,得到不同混凝土强度等级下主梁结构极限荷载系数,C45、C50、C55、C60混凝土的极限载荷系数分别为8.52、8.58、8.75、8.85。
由图4可以得出:混凝土强度等级对主梁的结构极限荷载系数有一定影响。采用C60混凝土时,结构的极限荷载系数最大;与前者相比,混凝土标号为C45、C50、C55时,极限荷载系数分别减少3.73%、3.05%和1.13%。随着混凝土强度的增大,结构的极限承载能力稍有增加。
由图4可知,不同的混凝土强度对梁拱组合连续刚构桥主墩及主梁的结构极限承载能力均有影响,不同主墩、主梁混凝土强度作用下,梁拱组合刚构桥的竖向挠度由两主墩向中跨跨中逐渐增大,中跨跨中变形最大,结构主墩中跨侧下弦主梁的应力较大,最大应力出现在主墩中跨侧下弦主梁3/8处。在外荷载作用下,梁拱组合刚构桥最先从主墩中跨侧下弦主梁3/8处及中跨跨中截面处遭到破坏。
3.3 边中跨比
梁拱组合刚构桥存在空腹节段,因此,不同的边中跨比对主墩及主梁的受力情况影响较大。取边中跨比μ分别为0.40、0.45和0.50时分析梁拱组合刚构桥的极限承载力,工程主桥跨径布置为140 m+245 m+190 m+130 m+80 m,分别取桥跨布置为98 m+245 m+98 m,110.25 m+245.00 m+110.25 m,122.5 m+245.0 m+122.5 m 3种。
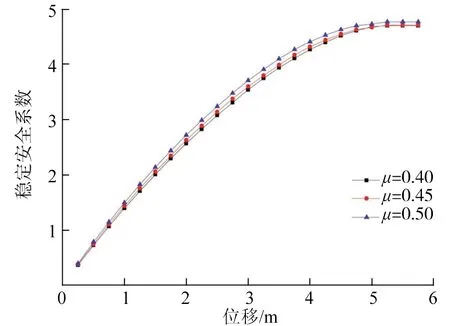
图5 不同边中跨比对应控制点的 稳定安全系数-位移曲线
通过同时考虑几何非线性及材料非线性的双重非线性分析,得到不同边中跨比对应的结构控制点的荷载-位移曲线,如图5所示。
通过计入几何及材料双重非线性因素的非线性静力弹塑性分析,得到边中跨比分别为0.40、0.45、0.50时,极限荷载系数分别为4.70、4.71、4.77。
由图5可得:不同的边中跨比对结构的极限荷载系数影响较小,边中跨比为0.40~0.50时,结构变形由两主墩向中跨跨中逐渐增大,主跨跨中变形最大。结构两主墩中跨侧下弦主梁所受应力普遍较大,在中跨侧下弦主梁3/8处应力最大,下弦主梁根部向融合区所受应力先增后减再增。两主墩边跨侧应力相对较小,且越接近融合区段应力越大。在外荷载作用下结构最先从两主墩中跨侧下弦主梁3/8处及跨中截面处发生破坏。随着边中跨比的增加,结构的极限承载能力略有增加,边中跨比由0.40变为0.45和0.50时,结构的极限荷载系数依次提高0.21%、1.49%,增加较少。
3.4 截面空腹率
与空腹式连续刚构桥相比,梁拱组合刚构桥空腹节段更长,空腹面积更大。箱梁根部腹板挖空使得自重大大减小,同时降低墩顶附近的负弯矩,空腹节段空腹面积对梁拱组合刚构桥的内力影响较大。
梁拱组合刚构桥的截面空腹率是指上下弦梁内轮廓所围面积A1与上下弦梁中心线所围面积A2(阴影面积)之比,即η=A1/A2,如图6所示。

图7 不同截面空腹率对应控制点的稳定安全系数-位移曲线
取空腹率分别为0.50、0.55和0.60时对梁拱组合连续刚构桥的极限承载力进行非线性分析,得到不同空腹率对应结构控制点的荷载-位移曲线,如图7所示。
通过计入几何及材料双重非线性因素的非线性静力弹塑性分析,得到截面空腹率分别为0.50、0.55、0.60时,极限荷载系数分别为4.35、3.86、3.40。
由图7可得:不同的截面空腹率对结构的极限荷载系数有较大影响,而对结构的破坏形式和破坏位置影响较小。空腹率为0.50~0.60时,结构变形由两主墩向中跨跨中逐渐增大,中跨跨中变形最大,结构主墩中跨侧下弦主梁所受应力较大,最大应力出现在主墩中跨侧下弦主梁1/2处。在外荷载作用下,结构最先从主墩中跨侧下弦主梁1/2处及跨中截面处发生破坏。随着空腹率的增加,结构的极限荷载系数逐渐减小。空腹率由0.50变为0.55和0.60时,结构的极限荷载系数依次降低了11.26%和21.84%,降幅增加。梁拱组合刚构桥根部的空腹面积对结构的承载能力有较大的影响,随着空腹面积的增加,下弦主梁与上弦主梁纵轴水平夹角越来越小,下弦主梁受力更趋向梁体结构,除承受压力之外,还要承担弯矩。

a)上弦梁 b)下弦梁
3.5 弦梁刚度比
上下弦梁断面形状如图8所示。
上下弦梁的刚度比为上弦梁面内抗弯刚度Efirst与下弦梁面内抗弯刚度Elast之比,即γ=Efirst/Elast。上下弦梁相对刚度的改变引起结构断面及全桥内力分布的改变,上下弦梁刚度比对梁拱组合连续刚构桥内力分配影响较大。
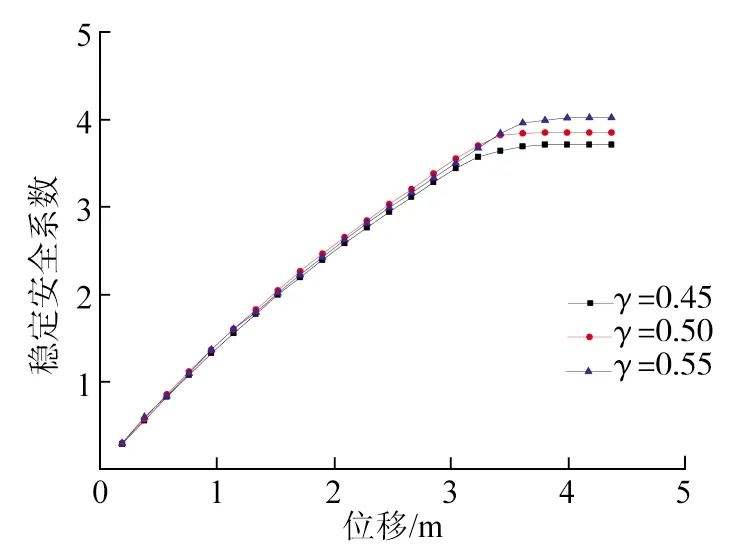
图9 不同弦梁刚度比对应控制点的稳定安全系数-位移曲线
取上下弦梁刚度比分别为0.45、0.50和0.55时对梁拱组合连续刚构桥的极限承载力进行分析研究,通过同时考虑几何非线性及材料非线性的双重非线性分析,得到不同弦梁刚度比对应的结构控制点荷载-位移曲线,如图9所示。对比分析时,除改变上下弦梁的面内刚度外,其余参数与依托工程相同。
通过计入几何及材料双重非线性因素的非线性静力弹塑性分析,得到上下弦梁刚度比分别为0.45、0.50、0.55时,极限荷载系数分别为3.72、3.86、4.03。
由图9可知:不同的上下弦梁刚度比对结构的极限荷载系数有一定影响,上下弦梁刚度比为0.45~0.55时,结构变形由两主墩向中跨跨中逐渐增大,中跨跨中变形最大,结构主墩中跨侧下弦主梁所受应力较大,最大应力出现在主墩中跨侧下弦主梁3/8处,在外荷载作用下,结构首先从下弦主梁3/8处及上下弦梁融合处发生破坏。随着上下弦梁刚度比的增加,结构的极限荷载系数略微增加。上下弦梁刚度比由0.45变为0.50和0.55时,结构的极限荷载系数依次增加3.76%和8.33%。空腹节段的弯矩按照上下弦梁的相对刚度比进行分配,在荷载作用下,不同的弦梁刚度比使得上下弦梁分配的荷载大小不同。
4 结论
1)混凝土标号对主墩及主梁的结构极限承载能力均有影响,但对破坏位置影响不大。随着混凝土强度的增加,结构的极限荷载系数略有增大,结构的破坏位置最先均出现在主墩中跨侧下弦主梁3/8处及跨中截面处。
2)边中跨比对结构的极限荷载系数和结构破坏位置影响均较小。边中跨比为0.40~0.50时,梁拱组合连续刚构桥下弦主梁受力较大,上弦主梁受力小,主桥中跨跨中截面变形最大,在外荷载作用下结构的破坏均由两主墩中跨侧下弦主梁3/8处及跨中截面开始。结构的极限荷载系数随边中跨比的增加而略有增加。
3)截面空腹率对结构的极限荷载系数影响很大,而对结构的破坏位置影响较小。不同截面空腹率下梁拱组合连续刚构桥主墩中跨侧下弦主梁受力较大,上弦主梁受力较小,主桥中跨跨中截面的变形最大。在外荷载作用下,结构首先从主墩中跨侧下弦主梁1/2处及跨中截面处发生破坏,空腹率为0.50~0.60时,结构的极限荷载系数随空腹率的增加而逐渐减小。
4)上下弦梁的刚度比对结构的极限承载能力有一定影响,但对结构的破坏位置基本没有影响。不同弦梁刚度比作用下梁拱组合连续刚构桥主墩中跨侧下弦主梁受力较大,特别是在下弦主梁3/8处及上下弦梁融合处,而上弦主梁受力较小,主桥中跨跨中截面的变形最大。在荷载作用下,结构首先从下弦主梁3/8处及上下弦梁融合处发生破坏。上下弦梁刚度比为0.45~0.55时,结构的极限荷载系数随上下弦梁刚度比的增加而略微增加。
