水下掩埋物目标强度仿真分析
2020-07-13李嘉旺
李嘉旺, 李 威,2,3
(1. 华中科技大学 船舶与海洋工程学院,武汉 430074;2. 高新船舶与深海开发装备协同创新中心,上海 200240;3. 船舶与海洋水动力湖北省重点实验室,武汉 430074)
0 引 言
海底掩埋物的探测[1-3]一直以来都是受到国内外学者关注的热门话题,预报掩埋物的准确位置和掩埋深度等信息对海洋资源勘探、海底沉船打捞、废弃鱼雷清理等实际工程工作有很大的指导意义,为此国内外学者从不同方向都做出努力。凯文·L.威廉斯(Kevin L. Williams)[4]、安东尼·L.博诺莫(Anthony L. Bonomo)[5]基于Biot理论提出等效密度模型(effective density fluid method, EDFM),将泥沙的多孔介质模型等效成液体模型。该模型对于声的反射及透射特性与完整的Biot理论预报基本相同,并且与Biot理论模型相比减少了很多难以直接测量的参数,更加方便计算。于盛齐等[6]根据等效密度流体近似反射模型对不同掠射角下的海底反射损失进行了探究。彭临慧等[7]探究了声波在水-多孔介质海底界面上的反射和透射特点。于福建等[8]探究了粗糙海底对掩埋物的目标强度的影响。目前常用的三维计算软件无法实现对多种计算域材料的上下分层,且目标物偏离计算域中心存在于其中一种或某几种的材料之中的情况进行远场计算。本文主要针对二维轴对称目标,结合COMSOL二维轴对称模块,利用声学有限元方法(FEM)[9-13]与完美匹配层(PML)技术,并通过等效密度流体模型代替海底泥沙多孔介质模型,结合(Helmholtz-Kirchhoff)积分公式及球面波分层介质[14]中的折射原理,计算分析掩埋物的目标强度特性。
1 分层介质中的声散射
Helmholtz-Kirchhoff远场积分如式(1)所示。
(1)
式中:r为远场中一点;r0为目标表面上一点。为得到远场中任意一点处的散射声压,需要求得掩埋物表面任意一点的声压、位移以及相应的Green函数[15]。我们可以借助COMSOL软件计算得到掩埋物表面声压和位移,相应的Green函数可由分层介质中的声散射原理推导获得。
声波从远场辐射器O点出发,并在海水与等效密度流体分界面上按照折射定律通过,最终到达等效密度流体中掩埋物表面上一点S处。示意图如图1所示。
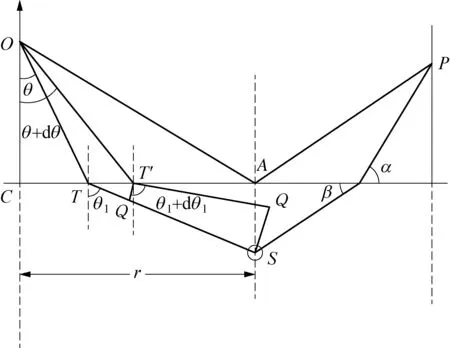
图1 分层介质中的声折射示意图Fig.1 Schematic diagram of acoustic refraction in layered media
由折射定律可知,入射角θ与折射角θ1的关系如式(2)所示。
nsinθ1=sinθ
(2)
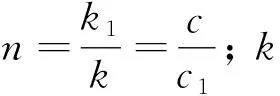
掩埋物表面上一点S的声波振幅可以由射线管内流守恒定律获得,而相位则由波的传播路程确定。
(3)
式中:OT、TS是声波传播路程长度。根据折射定律,我们可以得到
(4)
式中:D=-z,是掩埋物表面一点S到分界面的距离。为了确定点S上的声波的振幅,我们在平面OTS之内,并以角度θ+dθ入射到分界面上OT′Q。假定T点处下层介质中的振幅为A(T),掩埋物表面一点S处的振幅为A(S)。由射线管内能流守恒定律,可知
(5)
T点位于分界面上,其在海水介质中的场φ与在等效密度流体介质中的场φ1的关系如式(6)所示。
(6)
式中:
(7)
在建立了直达波和反射波的分界面上方,总场的振幅等于
(8)
式中:
(9)
又因为A(T)=|φ1|,所以点S处的场φ(S)如式(10)所示。
(10)
式中:z0为远场点O到分界面的距离。故从等效密度流体介质中经分界面到海水介质中的远场点的场函数φ(P)可由φ(S)变换而来。变换方式为1/m替换m、 1/n替换n。故相应的Green函数如式(11)所示。
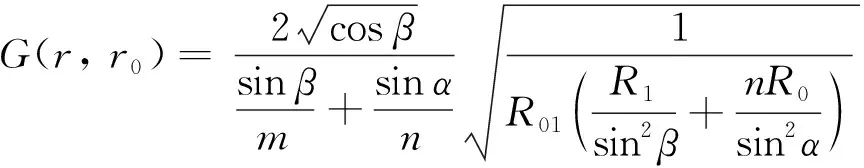
(11)
式中:R0为分界面折射点到远场点的距离,R1为掩埋物表面一点S到分界面折射点的距离,R01为掩埋物表面一点S到远场点的水平距离。
此我们可求得海水介质中远场中任意一点声压P(r)。进而求得海底泥沙掩埋物的声目标强度,如式(12)所示。
(12)
2 计算流程及验证
本文研究以半径为0.2 m的钢制实心球为目标物,水域网格大小为5 mm,球体网格大小为5 mm,取球体网格大小的1/10为0.5 mm。水域上、下、右侧布置40 mm宽度完美匹配层(perfectly matched layer, PML), PML设置8层网格。自由场中计算模型示意图如图2所示。
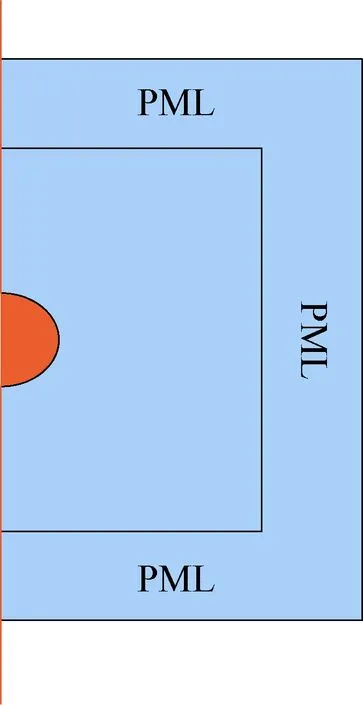
图2 计算模型示意图Fig.2 Schematic diagram of calculation model
海水及钢制实心球的材料参数如表1所示。

表1 材料参数
结合自由场中的Green函数计算ka在0~8范围内水下弹性实心球体的散射声场,结果如图3所示,使用二维轴对称模块并结合远场积分公式的方法与简正级数解的计算结果吻合得很好。说明对于轴对称目标,这种计算方法可以有效地、准确地代替三维模型进行计算分析。同时按照上述网格大小进行划分,三维模型有网格200万余个,计算时间超过7 h;使用二维轴对称模型有网格19 836个,计算时间约为9 min 31 s。在保证精度的同时,极大地提高了计算效率。
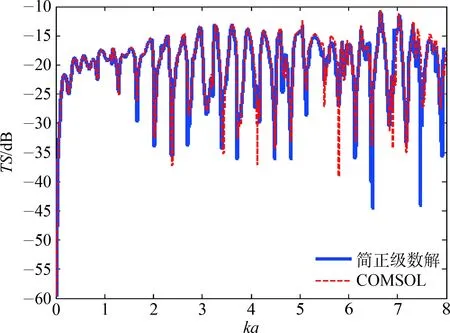
图3 自由场中钢制实心球声目标强度对比Fig.3 Comparison of acoustic target strength of steel solid sphere in free field
3 掩埋物目标强度计算分析
掩埋状态下的声散射场数值计算,采用与自由场中相同的网格划分方式及网格大小,掩埋状态下声散射场数值计算模型及网格局部如图4和图5所示。
计算模型分为上下两层,上层介质为海水,下层介质为等效密度流体,钢制实心目标物掩埋在下层介质中,液体介质的上、下、右侧均设置40 mm宽的完美匹配层。图4左侧橙黄色线为旋转对称轴,绕轴旋转360°即可得到三维计算模型。上下介质中海水、等密度流体、钢制实心球均采用三角形网格,钢制实心球表面采用域网格大小1/10的三角形网格,PML采用映射方式得到大小均匀的四边形网格。
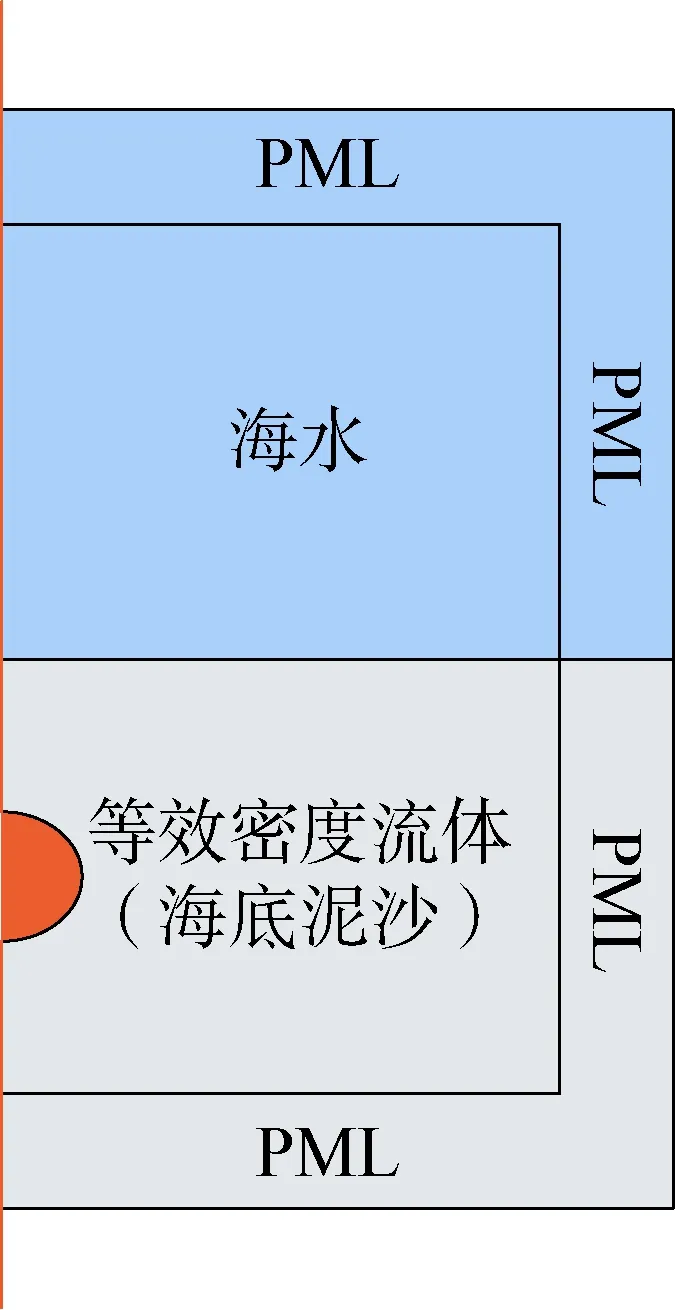
图4 计算模型示意图Fig.4 Schematic diagram of calculation model
入射声场的声压幅值大小为1,方向由上层介质垂直入射到下层介质中,结合表2中等效密度流体参数,计算ka在0~8范围内的掩埋目标的散射声场,得到三维散射声压图,如图6所示。
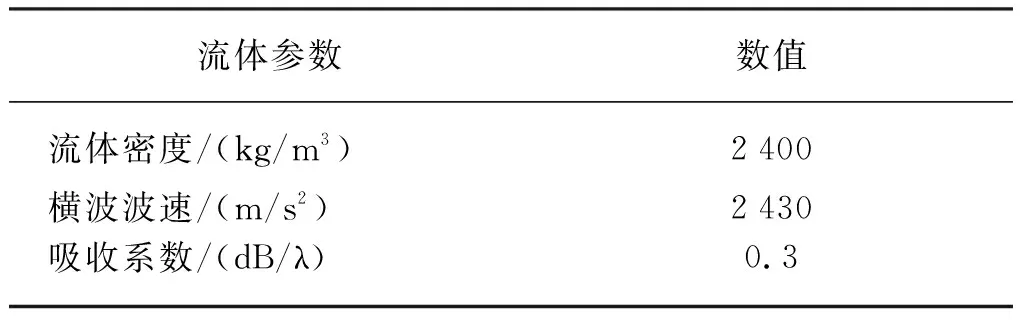
表2 等效流体参数
ka=0.2
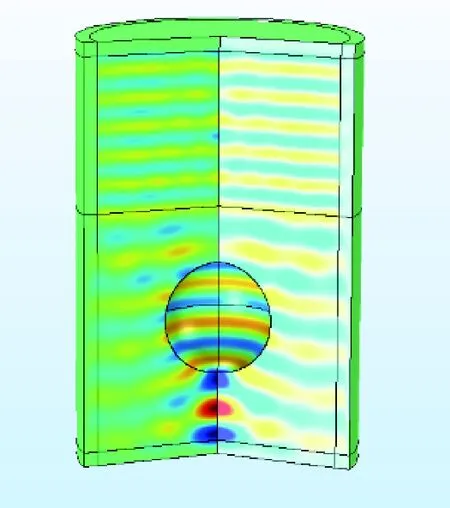
ka=2
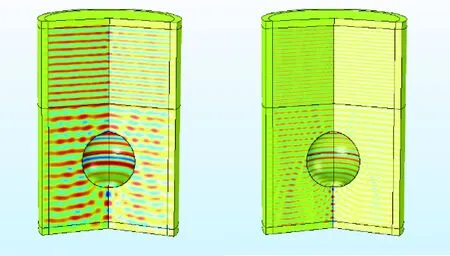
ka=4 ka=8图6 散射声场示意图Fig.6 Schemc diagram of scattering sound field
利用式(11)的Green函数和COMSOL软件中得到的目标物表面的声压和位移,求得远场中一点的声压,运用目标强度式(12),得到掩埋物的目标强度。
目标仍为半径0.2 m的钢制实心球,远场信号接收点选取目标物正上方1 000 m远处一点。计算ka在0~8范围内等效密度,分别取1 920 kg/m3、 2 400 kg/m3、 3 200 kg/m3,等效声速分别取2 230 m/s、 2 430 m/s、 2 630 m/s,吸收系数分别取0.5 dB/λ、 1 dB/λ、 2 dB/λ。
掩埋深度取1r(r为目标物半径),计算掩埋物的目标强度随等效密度、等效声速、吸收系数变化的规律图。
如图7~图9所示,等效密度、等效声速、吸收系数的变化不会改变目标强度曲线的波峰数量和形状及波峰波谷的位置。当等效密度提高时,目标强度不断降低,但在波谷位置会出现密度增大,目标强度提高的现象。当等效声速提高时,目标强度不断降低,并且随着频率的提高,降低的程度不断提高。吸收系数增大时,目标强度不断降低,并且随着频率的提高,降低的程度不断提高。在同一频率下,目标强度的改变量与吸收系数成正相关。
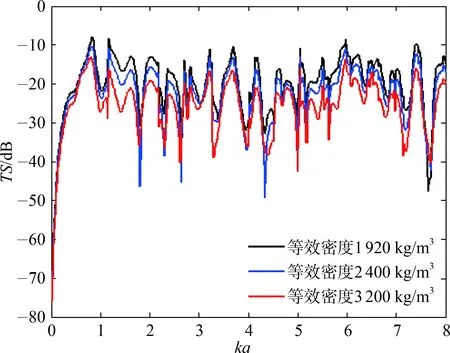
图7 目标强度随等效密度变化曲线Fig.7 Curve of target strength with equivalent density
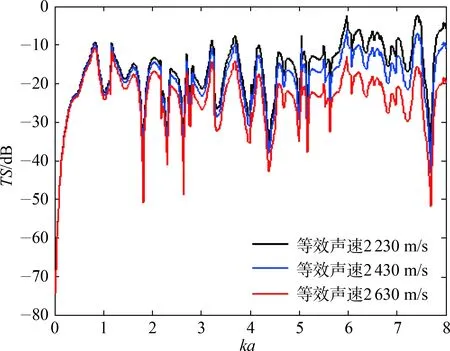
图8 目标强度随等效声速变化曲线Fig.8 Curve of target strength with equivalent sound speed
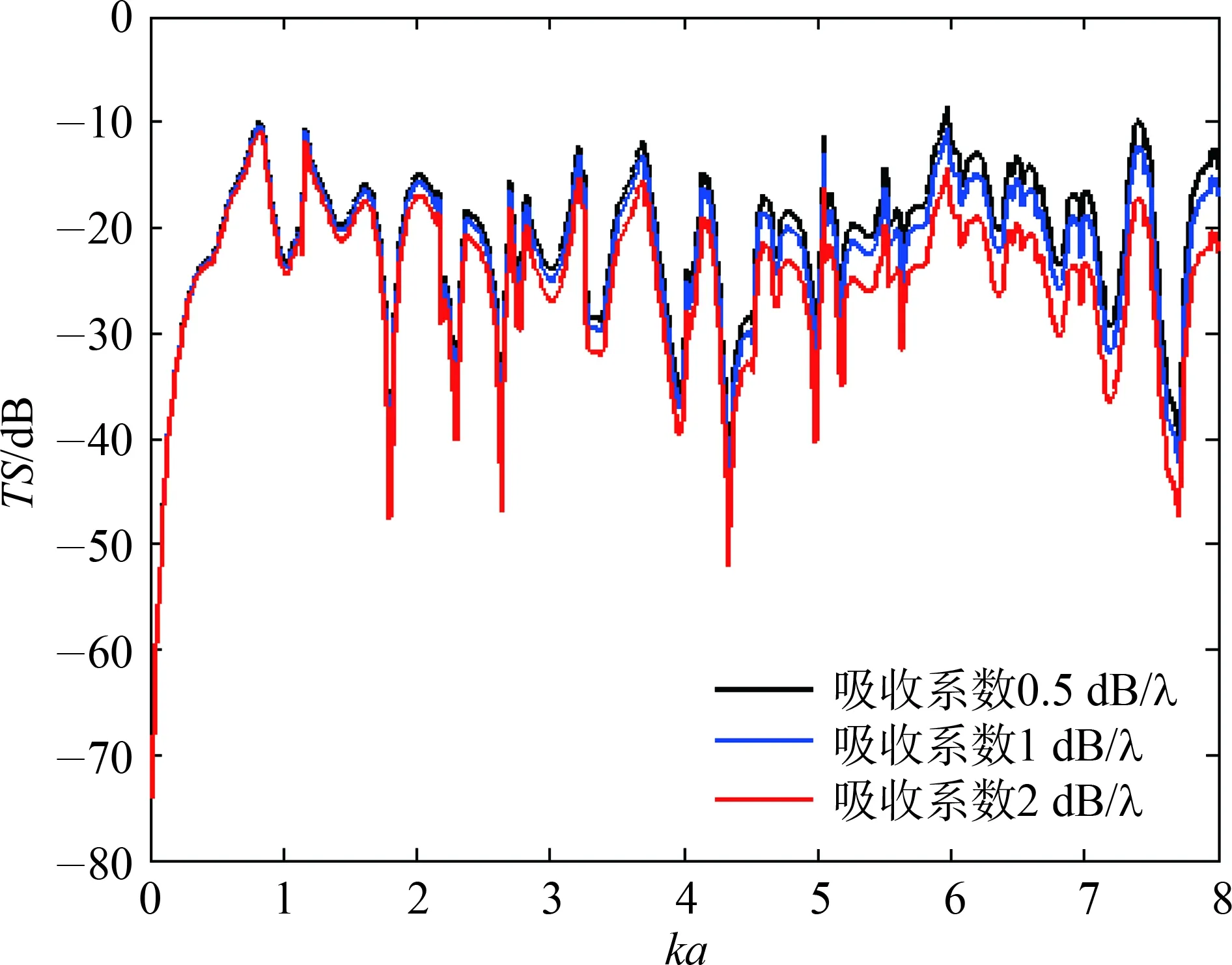
图9 目标强度随吸收系数变化曲线Fig.9 Curve of target strength with absorption coefficient
在等效密度为2 400 kg/m3、等效声速为2 430 m/s、吸收系数为0.3 dB/λ的情况下,掩埋深度分别取0.1r、 1r、 2r。得到掩埋物的目标强度随掩埋深度变化的规律图。
如图10所示,掩埋深度的改变不会改变目标强度曲线的波峰数量和形状及波峰波谷的位置。随着深度的不断增加,目标强度逐渐降低,降低程度随频率的增加而不断增加。
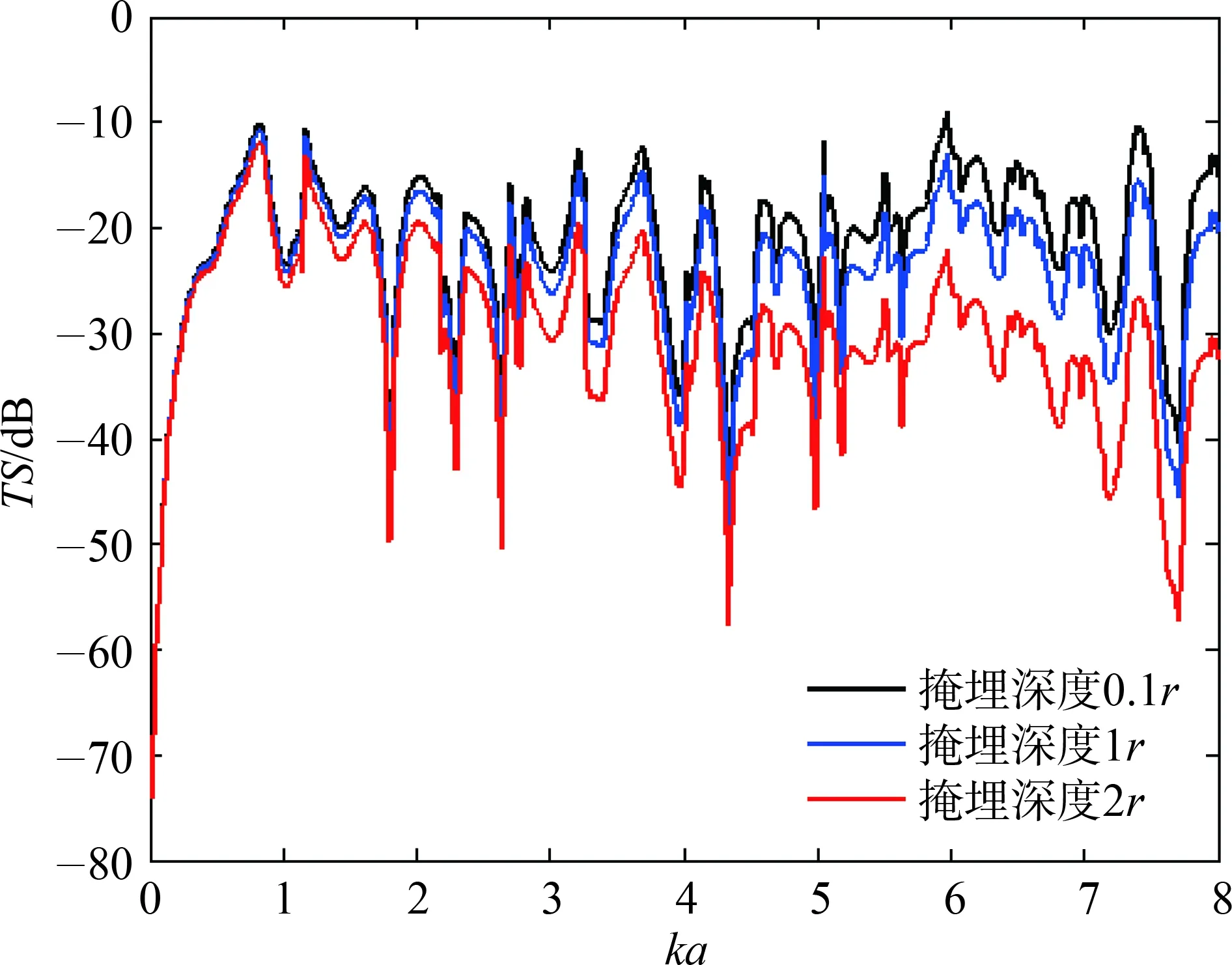
图10 目标强度随吸收系数变化曲线Fig.10 Curve of target strength with absorption coefficient
4 结 语
本文利用COMSOL软件二维轴对称模块,结合推导的分层介质中Green函数和等效密度流体方法(equivalent density fluid method, EDFM),借助Helmholtz-Kirchhoff远场积分公式,得到了掩埋物的目标强度随等效密度、等效声速、吸收系数、掩埋深度变化的规律。这4种物理量的变化均不改变目标强度曲线的形状及波峰波谷的位置,掩埋物的目标强度随这4种物理量的增大而不断降低,并且降低程度随频率的增加而不断加深。为海底掩埋目标的探测提供了一定的理论依据。在后续的工作中将继续探究在半掩埋形式下及复杂水-沙的分界面形状等情况下,目标的声散射问题。
