基于NARX神经网络的FPSO系泊缆张力预报
2020-07-13邓林青朱耀文王宏伟张勇青李彤滨
邓林青, 朱耀文, 王宏伟, 张勇青, 李彤滨
(1. 中海石油深海开发有限公司,深圳 518067;2. 哈尔滨工程大学 船舶工程学院,哈尔滨 150001;3. 海洋石油工程股份有限公司,天津 300451)
0 引 言
浮式生产储卸油平台FPSO(floating production storage and offloading)在海洋石油勘探开发中被广泛应用,一般采用系泊系统限制其在海面的运动。由于人类对资源需求的日益增长,海洋油气的开发不断走向深海,从而使浮式平台及其附属系统面临更为恶劣的海况[1]。为了保证各类平台的安全作业,浮式结构的运动响应范围以及系泊缆的张力极值必须在规定的范围之内。因此,在设计初期,需要借助复杂的时域耦合分析软件,对复杂的外部环境荷载进行相应的计算与分析。在外部风、浪、流等载荷的联合作用下,浮式结构运动与系泊及立管系统之间的耦合作用不能忽视,深水细长结构物显著的动态特性也需要准确地模拟,这些因素将导致整个系统在时域仿真求解时需要耗费较多的计算时间。
当前已有大量的研究投入到寻求一个可靠的、耗时较少的浮式结构系泊系统耦合分析方法[2-4]。人工神经网络是一种基于数据驱动的方法,在输入与输出之间起到了类似传递函数的作用,适用于寻找随机输入与相应输出之间的映射关系,其在船舶与海洋工程领域已经得到了广泛的应用,包括浮式结构及其系泊系统设计参数的优化,波浪有义波高、环境荷载、船舶运动的预报,缆线与结构的疲劳分析等[5-8]。Guarize等人[9]提出了一种基于人工神经网络与有限元模型的混合方法,用于细长海洋结构物的时域动态分析,前期使用仿真软件得出短时间内的结果,作为神经网络的训练数据,将已知的浮体运动输入训练好的神经网络中进行张力预报,得到一个长期的时域响应。孙丽萍等人[10]将BP神经网络和遗传算法相结合,对FPSO系泊系统的长度进行优化,缩短了优化所需的时间。张隆辉等人[11-12]在构建系泊系统主动式截断仿真过程中,使用NARX神经网络模型代替了传统缆索数值模型,用于预报系泊线截断点的运动响应。该模型能够加快计算求解的速度,有助于主动式混合模型试验的实现。Pina[13-15]使用NARX神经网络进行了系泊线和立管的力学分析。以浮体的运动为输入参数,系泊和立管的顶端张力为输出参数,通过对比神经网络模型预报结果与有限元计算结果,验证了该模型能够准确地预报顶端张力,并具有较高的计算效率。随后,将小波函数作为激活函数,使用小波神经网络代替传统的有限元仿真,进行海洋细长结构物的分析。上述方法均是基于预先规定的浮体运动,没有考虑浮体与系泊系统之间的耦合作用。为此,本研究将波浪的时历升高作为神经网络模型的输入参数,使用神经网络模型进行浮式生产系统的时域耦合分析。
本文将NARX神经网络应用于某一分布式FPSO系泊系统时域耦合分析中,该模型包括两种训练模式,序列并行模式(NARX-SP)与并行模式(NARX-P)。前者需要将当前时间步之前的真实输出目标数据进行反馈,而后者需要将预报出的数据反馈回输入层,由于输出的真实目标数据无法提前得知,因此选取并行模式(NARX-P)进行训练与预报。首先使用OrcaFlex软件计算得到短时的时域耦合结果,以已知波浪的时历升高数据作为输入,系泊缆张力响应为目标输出,使该神经网络具有预报余下时间历程张力响应的能力。经比较发现,预报结果与时域耦合分析计算结果之间的最大相对误差为7.61%,而且该替代模型能够大幅减小数值仿真的时间。
1 NARX神经网络与实施方案
NARX神经网络是一种动态的循环神经网络,以误差反向传播的多层前馈神经网络(BPNN)为基础,引入了适当的延时参数与反馈作用。此神经网络的输出不仅取决于当前时间步的输入,还受到过去几个时间步神经网络输入、输出值的影响,在一定程度上能够缓解时域数据间存在的长期依赖问题,改善神经网络的性能,适用于时域非线性动态系统的预报,其作为一种强大的时域预报模型已被广泛地应用[16-17]。
1.1 神经元与激活函数
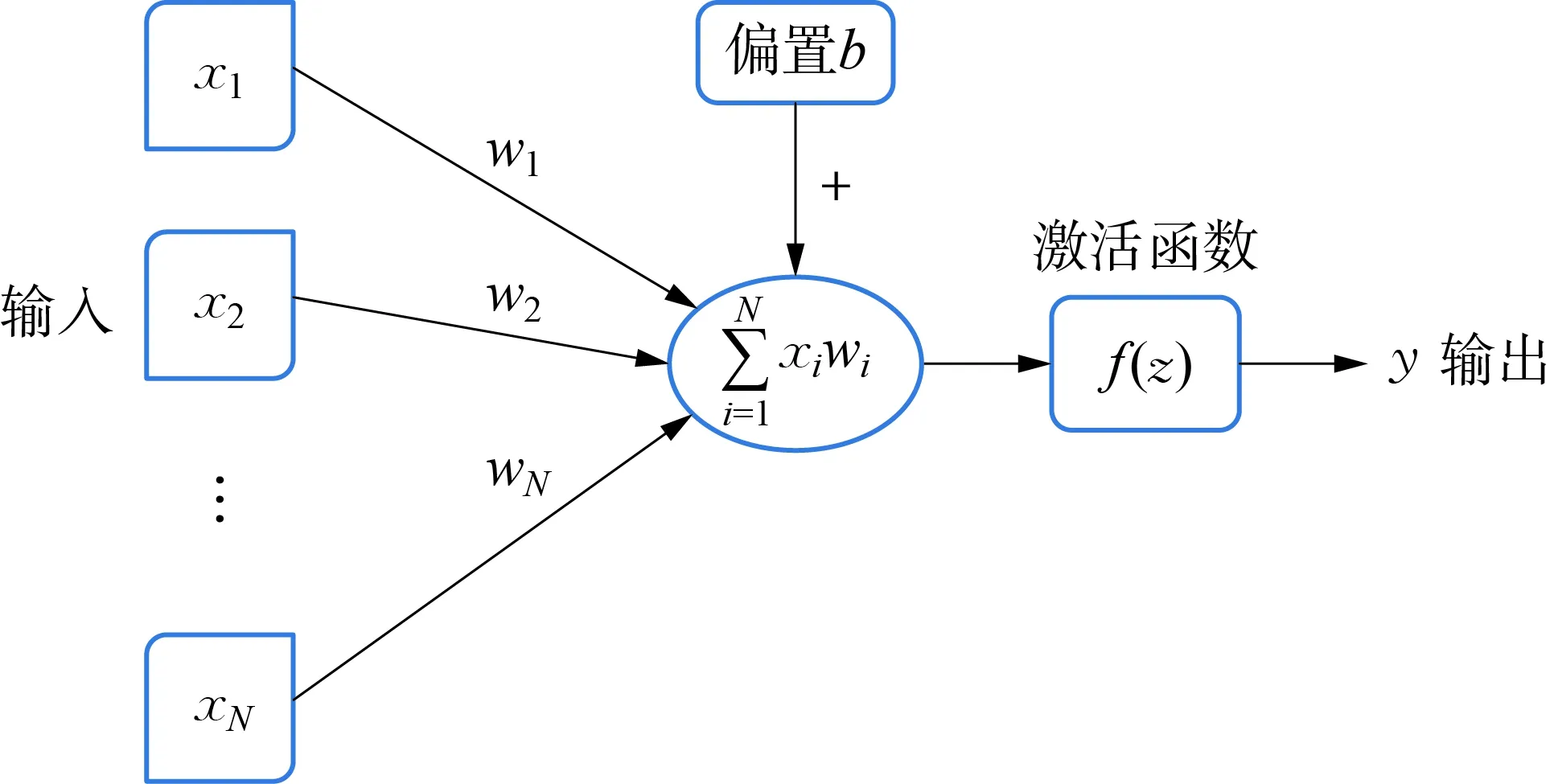
图1 McCulloch-Pitts模型Fig.1 McCulloch-Pitts model
神经元是神经网络的基础,也是神经网络的基本单元,其有兴奋和抑制两种状态。在一般情况下,大多数的神经元处于抑制状态,但是一旦某个神经元受到刺激,将导致它超过某个阈值,这个神经元就会被激活,处于“兴奋”的状态,进而向其他的神经元传递信息。1943年,心理学家McCulloch和数学家Pitts参考了生物神经元的结构,发表了抽象的神经元模型——MP模型,如图1所示。MP模型接受已知特征数据的输入xi,i=1,N,每个神经元使用权重wi、偏置b与输入数据进行线性组合后得到权值输出z,为了引入非线性特性,加权输出还需经过激活函数f(z)的转换得到输出y。MP模型的建立为神经网络的发展奠定了基础,但是由于其预先定义的权值无法进行学习,后来逐步提出了单层感知器、多层感知器以及误差的反向传播算法。当前各种形式的神经网络模型被不断地提出,广泛应用于各个领域。
神经网络已有多种激活函数可供选择,例如常用于分类问题的逻辑函数,以及用于回归问题的线性整流函数。本文使用的是如图2所示的双曲正切激活函数,它是一个值域具有上下界的连续函数:
(1)
式中:y为输出结果;z为加权输出。
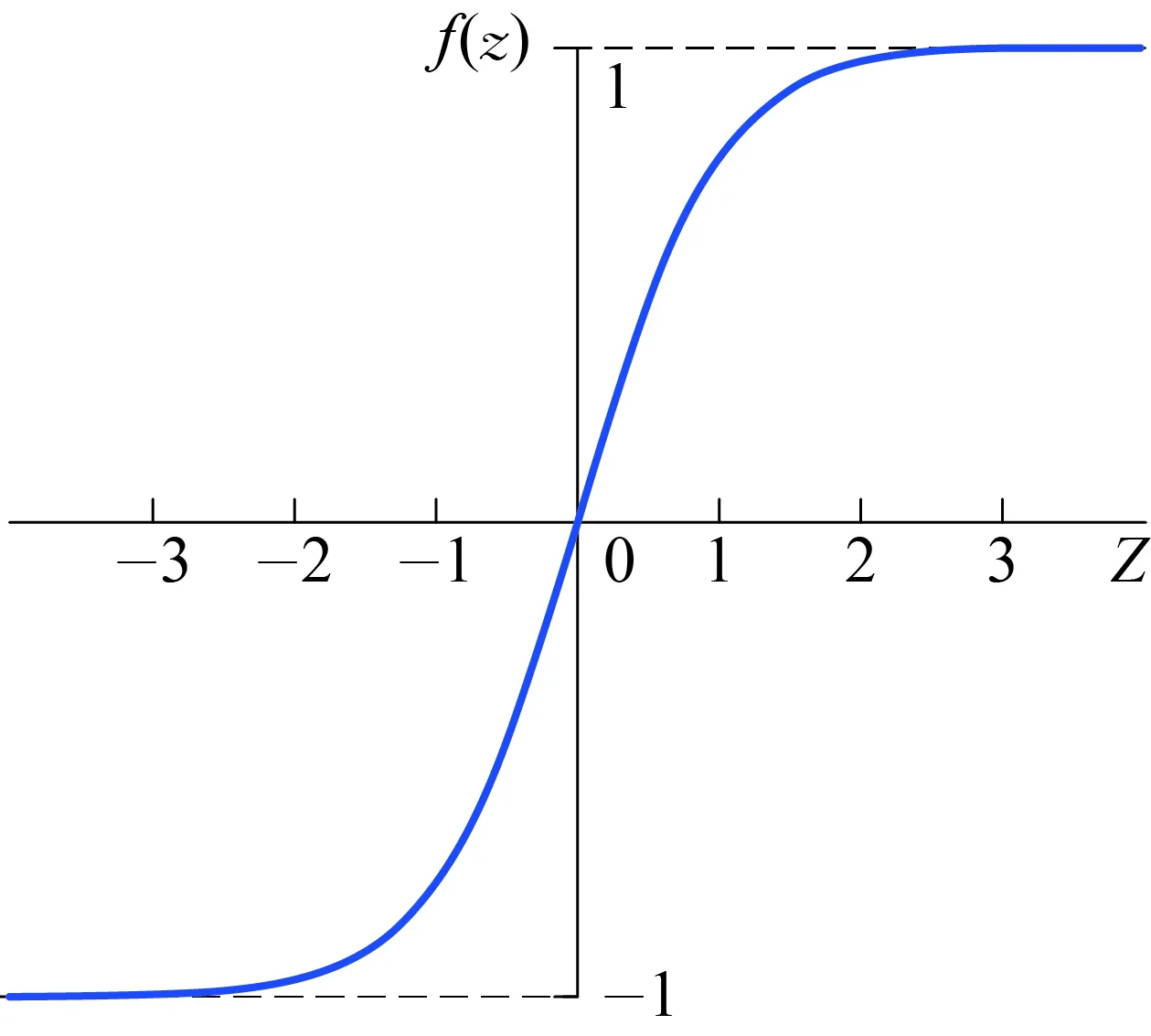
图2 双曲正切激活函数Fig.2 Hyperbolic tangent activation function
1.2 NARX神经网络结构
基于图3所示的双层BP神经网络(由于输入层未进行任何变换,没有作为单独的一层考虑)只包含了一个隐藏层,图4展示了NARX神经网络的结构。当前的神经网络输出不仅取决于当前和过去的输入,还取决于过去的输出,其输入集和最终输出结果可以分别表示为
X(t)=(x(t),x(t-Δt), …,x(t-pΔt),
y(t-Δt), …,y(t-qΔt))
(2)
yt=f(w,X(t))
(3)
式中:x(t)为神经网络的输入;yt为输出结果;w为权重参数;f(·)代表了NARX神经网络结构建立的映射关系模型;Δt为时域耦合分析所用的时间步长;p和q分别为输入与输出反馈的延迟阶数;pΔt和qΔt为延时的时间长度。输入与输出的延迟效应使得NARX具有了一定的记忆能力。
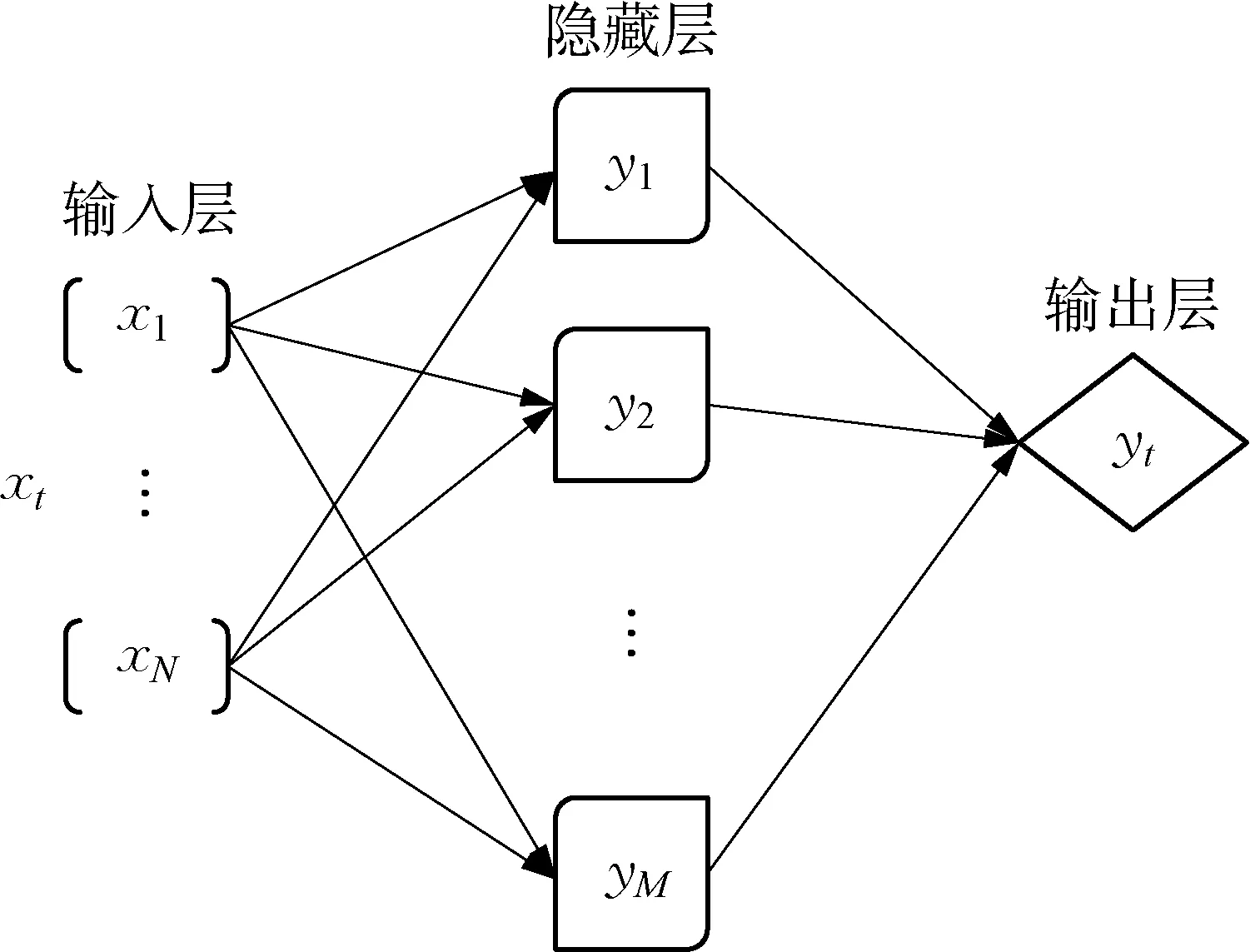
图3 双层BPNN结构Fig.3 Double-layer BPNN structure
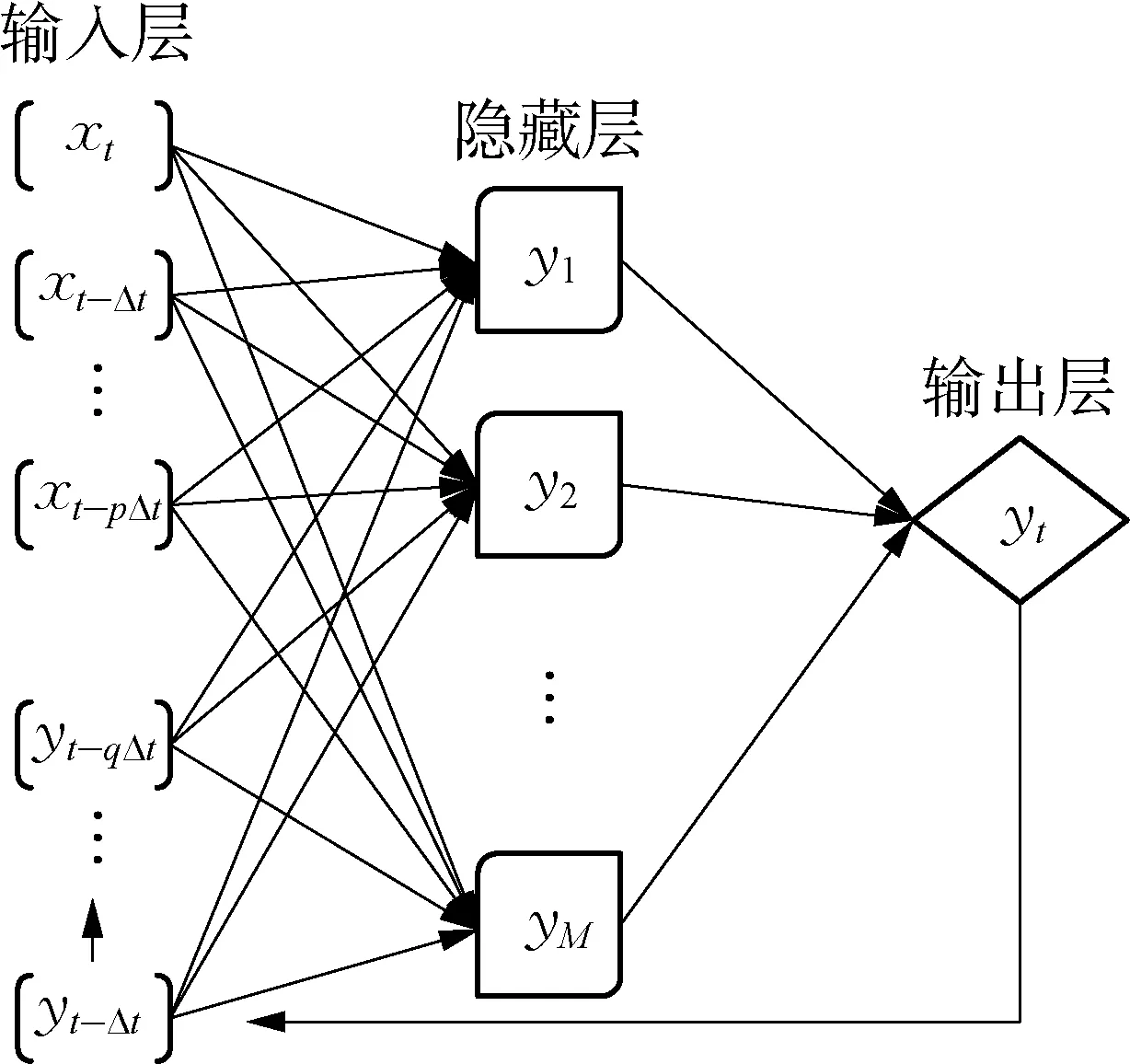
图4 NARX神经网络结构Fig.4 NARX neural network structure
神经网络模型输入参数的选择对于最终的结果有很大的影响。在浮式结构系泊系统时域耦合分析过程中,浮式结构水动力性能(AQWA软件预先计算)与外部的环境荷载是已知的条件,但这些都是不变的常数项,为了能够预报时域的输出,需要有相应的时域输入数据。文中选用波高的时历曲线作为输入,FPSO系泊系统的系泊线顶部张力值作为输出。
需要注意的是,NARX神经网络具有两种训练模式。第一种模式是序列并行模式(NARS-SP),这种方式的输入层由实际的目标值d(t)组成,即反馈回去的是实际的软件仿真结果,可表示为
X(t)=(x(t),x(t-Δt), …,
x(t-pΔt),d(t-Δt), …,d(t-qΔt))
(4)
另一种模式为并行模式(NARX-P),不同之处在于其将预报的输出反馈到输入层,如式(2)所示。在实际进行预报时,只有在训练集与验证集中的d(t)是已知的,可以通过OrcaFlex软件进行短时的时域耦合分析得到,而测试集的结果则使用训练完成的神经网络模型进行预报。
本文使用神经网络模型预报系泊线的顶端张力响应,以提高计算效率,减小时域耦合计算时间。由于无法得知当前时刻实际的张力值,因此使用NARX-P模式进行训练和预报。后续提到的NARX神经网络均表示使用NARP-P模式进行训练与预报的模型,该模型使用MATLAB提供的神经网络工具箱来完成[18]。
1.3 应用方案
如NARX此类的监督神经网络均需要一定数量的训练集进行训练,再通过验证集对模型的参数等进行适当的调整,最终运用到测试集上去预报未知的数据结果,这需要一个短时的时域耦合计算结果。同时,神经网络模型对训练集与验证集上的输入与输出数据必须是已知的,由于FPSO及其系泊系统在时域耦合分析过程中无法预先得知船舶运动时历数据,即无法使用船舶运动作为神经网络的输入参数。本文选择波高时历数据作为输入,系泊线顶端张力作为输出。
浮式结构系泊系统时域耦合运动模拟时间设置为3 h(10 800 s),计算步长为0.1 s。首先使用OrcaFlex软件计算800 s内的浮体系泊系统时域结果,其中600 s用于训练,200 s用于验证,每一个训练周期后,该模型都会预报验证集上的系泊张力,并与实际3 h数值模拟计算结果进行对比。如果在6个周期中验证集上的误差均呈现增长,则表明该模型无法继续优化,即完成训练,余下时间的张力响应可由建立的NARX神经网络模型预报得出。为了验证最终在测试集上的预报结果,文中进行了3 h的时域计算,实际使用时只需要计算短时目标数据(800 s)即可。实施方案如图5所示,其中的误差指的是均方误差:
(5)
式中:n为输入数据的数量;y(t)和d(t)分别为预报值和实际目标值。
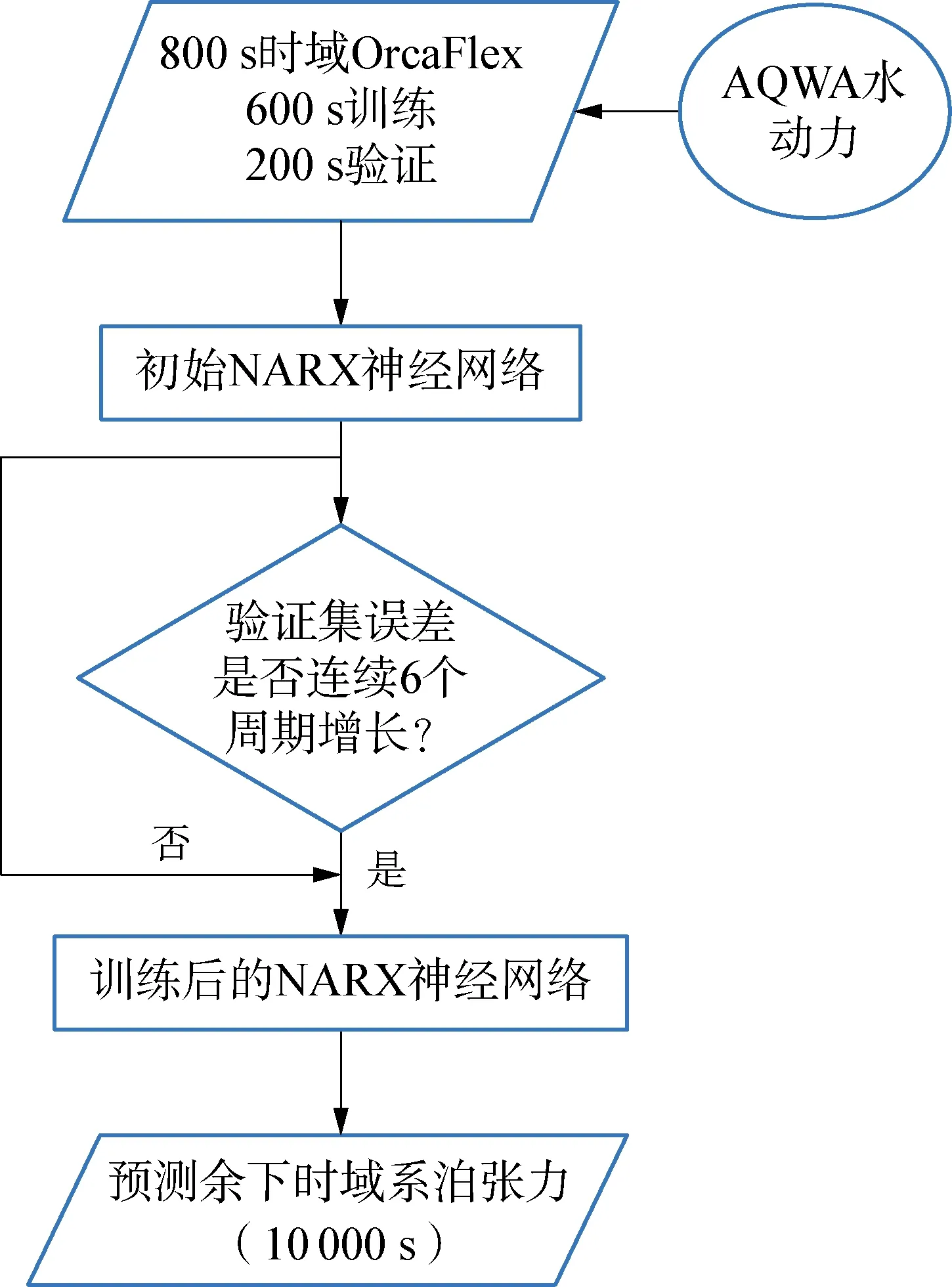
图5 NARX神经网络应用方案Fig.5 The application scheme of NARX neural network
2 数值计算分析
2.1 FPSO系泊系统模型与环境参数
上述方法被应用于某一分布式FPSO系泊系统,作业水深为1 200 m,平台与系泊缆的具体参数如表1和表2所示,共有12根系泊缆,分为4组,每组3根。每根系泊缆均链条-钢缆-链条三段材料构成,系泊编号及模型如图6所示。系统受到210°方向的风、浪、流的联合作用,表面流速为1.53 m/s,平均风速为25.6 m/s,波浪有义波高与峰值周期分别为7.25 m和19.78 s。在整个仿真过程中,流速与风速的大小和方向都是定常的,而波高是随时间变化的。为了预报系泊缆张力的时历输出,使用波高时历数据作为输入。波浪采用JONSWAP谱,可定义为
(6)
式中:α为能量尺度参数;γ为谱峰升高因子;σ为峰形参数;ωm为谱峰频率。

表1 FPSO平台参数
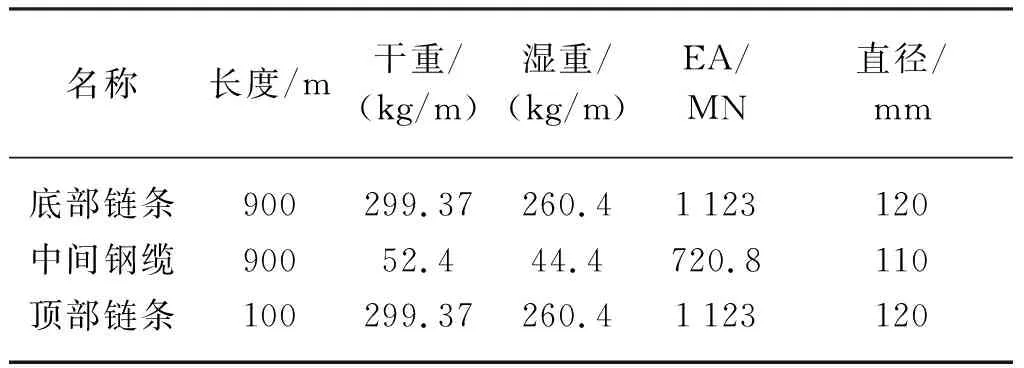
表2 系泊线参数
波浪谱确定后,即可以得到相对于空间某点的波面升高时历曲线。在OrcaFlex软件中可以得到整个时域过程的波高时域数据,这些数据在计算之前即可得知,这是前提条件。在实际应用时会发现,输入多点的波面升高更有利于NARX神经网络发现数据间的映射关系。因此,基于FPSO系泊系统静态平衡位置(-48.5, -55.6)处的波面升高时历曲线,再选择(-28.5, -35.6)、 (-38.5, -45.6)、 (-58.5, -65.6)、 (-68.5, -75.6),共五个点的波浪升高作为输入参数。图7给出了(-48.5, -55.6)位置处的波面升高时历曲线,上述静态平衡位置的计算也可以避免时域耦合分析时浮式平台的瞬态效应,防止不合理数据的生成。
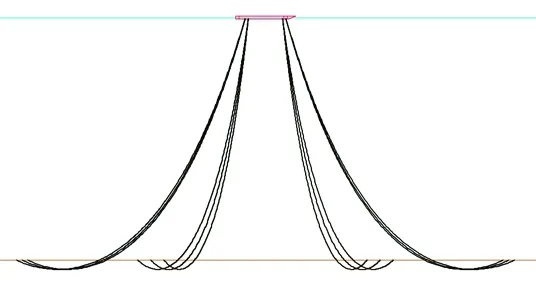
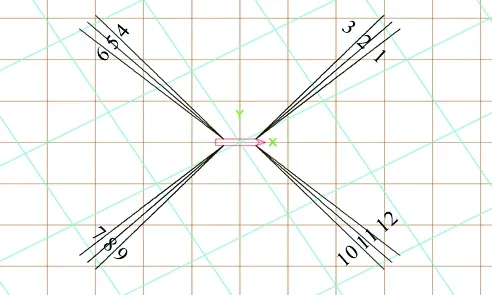
图6 FPSO系泊系统模型
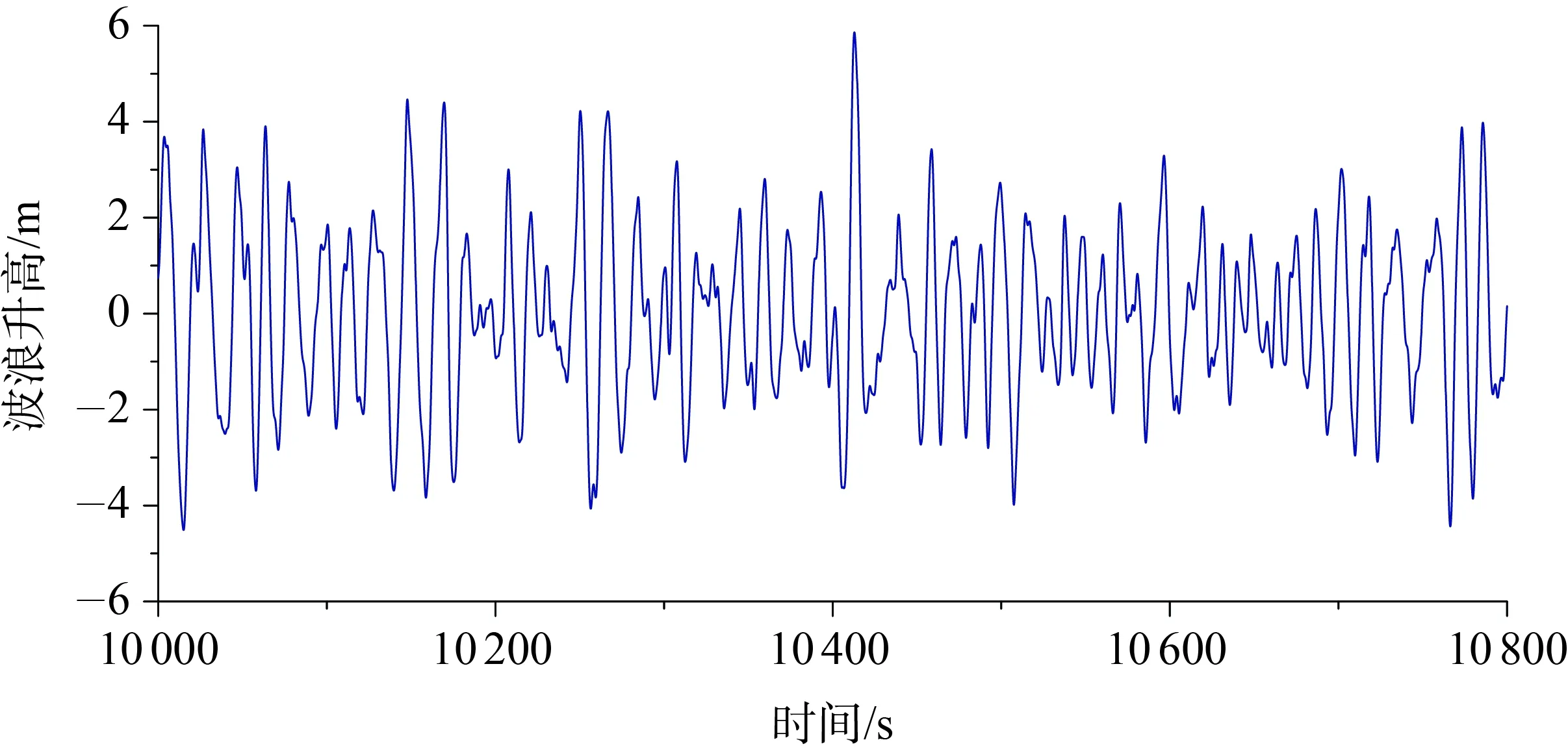
图7 波浪升高时历曲线Fig.7 Time history of wave elevations
2.2 超参数设定
首先使用OrcaFlex计算800s内的时域耦合数据,作为NARX神经网络的训练集和验证集。随后,需要确定该模型的输入与输出延迟数,以及隐藏层的神经元数量,这些超参数对神经网络模型的性能有很大影响。采用试凑法对隐藏层数和延迟数分别为5~20和5~30,间隔为5的区间范围内进行搜索,寻找结果较优的超参数,输入与输出使用相同的延迟数。选用系泊缆Line3,由于系泊缆张力量级较大,为了清晰地表示真实值与预报值之间的误差,表3展示的为均方根的误差。此处只给出了部分结果,当隐藏层神经元数为20时,输入与输出的延迟数为15时,均方根误差最小,为87.92 kN。在此过程中,NARX神经网络的训练也已经完成,当相应超参数确定后,即可用此参数下的NARX模型对测试集上的系泊缆张力进行预报。
一般神经网络的学习能力能够随隐藏层数与延迟数的增大而加强,但是太过复杂的神经网络结构会导致在训练过程中的过拟合问题,使其在验证集上的性能反而不好。网络层数太少又会导致训练时的欠拟合,使得该神经网络无法学习到输入和输出之间的关系。因此,对于超参数的正确选择是神经网络模型能否有效的关键因素之一,此处采用试凑法确定了一个较优的神经网络模型结构。
2.3 结果与分析
使用训练好的神经网络模型去预报余下10 000 s系泊缆Line3的时域张力结果,在此基础上,可以使用相同的神经网络结构进行系泊缆Line4的训练和预报。分别使用OrcaFlex软件和神经网络模型进行计算,图8~图11分别展示了2 000~2 400 s和10 400~10 800 s的Line3和Line4张力时历曲线对比结果。可见,预报结果与目标值(OrcaFlex软件计算结果)之间的时历曲线趋势几乎完全一致,结果吻合良好,但在每个时间段的峰值上略有差异。两种计算方式在时域结果上的相对误差如表4和表5所示,其中系泊缆顶端张力平均值的相对误差较小,系泊缆Line3和Line4张力最小值的相对误差分别为7.10%和7.61%,张力最大值的相对误差分别为5.33%和5.81%。整体上,相对误差的最大值为7.61%,在可接受的范围内。

图8 Line3顶部张力时域曲线2 000~2 400 sFig.8 Line3 top tension time series 2 000~2 400 s

图9 Line3顶部张力时域曲线10 400~10 800 sFig.9 Line3 top tension time series 10 400~10 800 s
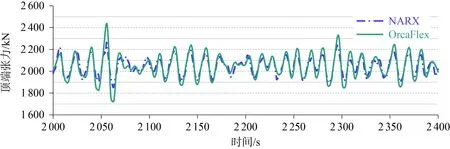
图10 Line4顶部张力时域曲线2 000~2 400 sFig.10 Line4 top tension time series 2 000~2 400 s
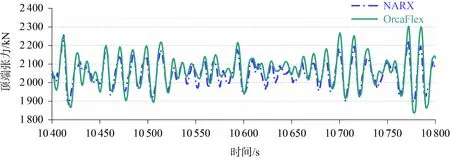
图11 Line4顶部张力时域曲线10 400~10 800 sFig.11 Line4 top tension time series 10 400~10 800 s
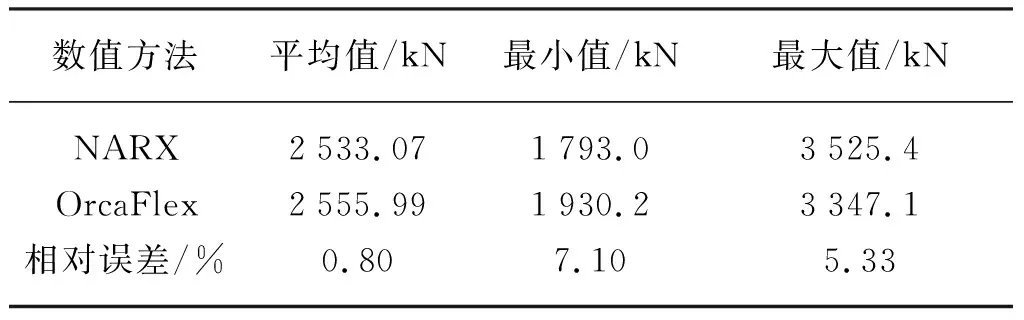
表4 Line3顶部张力时域数据分析
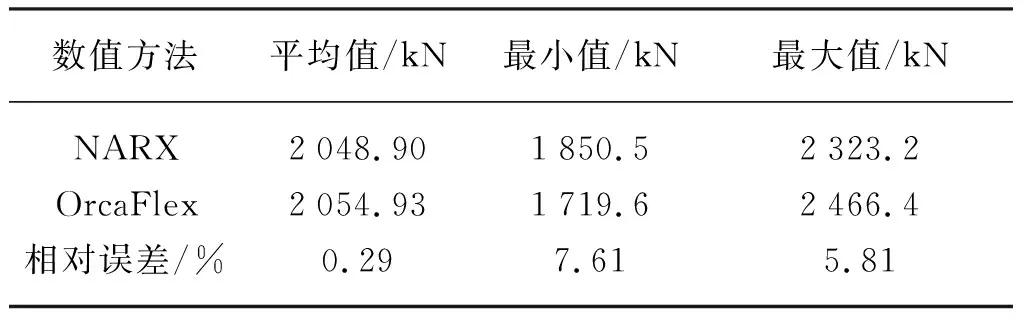
表5 Line4顶部张力时域数据分析
此种方法只需计算短时(800 s)时域耦合分析数据,使用神经网络模型预报其后10 000 s的系泊缆顶部张力,可以大幅减小OrcaFlex软件进行浮式结构系泊系统时域耦合分析的时间,计算效率大约为常规方法的13倍。这里的计算效率没有考虑神经网络构建以及训练、预报的时间,其中神经网络的构建,包括文中提到的超参数的选择会耗费相对较多的时间。但是,对于同一类的问题,使用相同或相近的网络结构,也可以得到较好的结果。本文中的神经网络结构与相关文献所用结构十分接近[13],使用了具有20个神经元的单隐藏层、延迟数为15的神经网络结构。
3 结 语
以某一分布式FPSO系泊系统为例,基于NARX神经网络模型进行FPSO系泊系统耦合分析中系泊缆顶部张力预报,对比OrcaFlex软件计算结果与NARX神经网络模型预报结果,可知两者的最大相对误差为7.61%。此方法是将OrcaFlex软件仿真计算与NARX神经网络模型相结合的一种方法,可以大幅减小软件时域耦合分析的时间,计算效率大约为常规方法的13倍。但是,文中使用的NARX神经网络模型只适用于上述浮式平台系泊系统的张力预报,如果需要更换浮式平台以及系泊系统的参数,则需要重新对该神经网络模型进行训练。
