重载铁路固定辙叉区轮轨瞬态滚动接触行为分析
2020-07-13徐井芒陈嘉胤
高 原,王 平,陈 嵘,徐井芒,陈嘉胤
(西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都 610031)

图1 固定辙叉及其典型损伤劣化
多体系统动力学为辙叉区轮轨系统动态相互作用分析的经典方法之一,该方法通过将轮轨系统视为通过不同形式铰接而成的刚体来求解轮轨接触行为。文献[1]基于SIMPACK软件建立道岔-车辆模型,结合道岔区轮载过渡区处的接触状态,分析了车辆过岔时的轮轨动态响应,并用实验验证了该模型的正确性及精确性。文献[2]基于多刚体动力学软件揭示了车辆直/侧向通过固定辙叉时的轮轨相互作用情况,探明了辙叉及曲线参数对轮轨冲击作用的影响,提出了直/侧向过岔时固定辙叉心/翼轨合理设计建议。文献[3-4]基于区间线路轮轨系统动力学方法,提出了道岔区轮轨动力学模型,将辙叉简化为变截面的欧拉梁,获取了车辆直向过岔时轮轨系统的竖向振动特性。文献[5]基于多刚体动力学软件及两种不同道岔及4种钢轨廓形下的轮轨耦合动力学模型,获取了不同道岔及钢轨廓形下的轮轨动态响应,得出截面几何廓形的改变对岔区轮轨动态作用影响较大,而车轮踏面廓形改变对轮轨相互作用影响较小的结论。文献[6]在充分考虑了道岔的变截面特性及轮轨多点接触状态的基础上,分别采用GENSYS和DIFF3D软件对比了不同频率下车辆过岔的动力性能,但仿真中道岔模型被假设为刚体,忽略了车轮荷载作用下轮对和轨道结构的变形。由于上述方法存在诸如轮轨视为刚体、线弹性及稳态滚动等假设,计算结果与实际情况有一定误差,且上述方法无法体现或模拟轮轨间振动沿钢轨纵向的传递特性。为了获取更为精确的结果,显式有限元方法逐渐被采用来模拟轮轨间动态行为。文献[7]基于有限元软件建立了标准轨为UIC54廓形的固定辙叉模型,并通过ABA方法验证了模型计算轮轨动态响应结果的精确性,探讨了车轮过岔时的动态蠕滑力、接触斑的黏滑特性、切向力及轮轨间微滑分布及大小等。文献[8-9]基于标准轨为UIC60廓形的固定辙叉有限元模型,探讨了车轮过岔时叉心的塑性变形、微滑,以及基于沿心轨纵向分布的最大摩擦功及摩擦功率云图。文献[10]结合实验及有限元方法对辙叉的动态冲击进行了分析,获取了车辆过岔时的黏滑分布及接触应力等,验证了自适应网格加密方式下有限元方法计算的精确性。文献[11]基于三维显式有限元模型求取了辙叉区轮轨瞬态滚动接触的法、切向接触解,结合Jiang-Swhitoglu疲劳准则预测了辙叉心轨处裂纹的疲劳寿命及裂纹扩展方向。文献[12]基于简化的车轮-辙叉显式有限元模型,分析了轮轨间冲击角和滚动接触半径对辙叉心轨处应力/应变场大小及分布特性的影响。在国内,基于辙叉的瞬态接触行为研究近乎空白,相关研究主要通过有限元与多体动力学相结合的方法,基于多体动力学计算出宏观轮轨力,利用Kalker简化理论[13]或有限元方法得出车轮和道岔间的接触解[14-15],但该方法无法反映轮轨间的动态相互作用特性,计算结果和实际相差较大。从上述分析可知,国外已开始发展并利用瞬态动力学来求解辙叉区轮轨相互作用,但大多针对标准轮轨型面,且主要关注车轮与固定辙叉的整体动力相互作用,然而重载铁路固定辙叉的伤损病害主要集中在轮载过渡范围内,且有关固定辙叉轮载过渡区轮轨瞬态接触行为及伤损特性的研究较少,因此利用显式积分法研究辙叉轮载过渡的瞬态接触行为非常有必要。
显式积分算法适用于求解需要分成微小时间增量来达到高精度的高速动力学问题,因此可用来精确模拟辙叉区结构不平顺所激发的瞬态相互作用。本文以重载铁路75 kg/m钢轨12号固定辙叉为研究对象,将现场实测的重载车轮踏面拟合为名义车轮踏面,建立车轮-固定辙叉三维轮轨瞬态滚动接触有限元模型,用于精确模拟车轮与辙叉间的动态相互作用,并详细分析固定辙叉轮载过渡区轮轨瞬态接触行为,在此基础上,结合材料安定图,对固定辙叉区接触伤损特性进行预测分析,并与固定辙叉的现场应用情况进行了对比验证,期望能为我国重载铁路固定辙叉的结构优化及养护维修提供理论指导。
1 计算模型
为揭示固定辙叉轮载过渡特性及其应力、应变分布规律,基于显式积分算法建立了典型75 kg/m钢轨12号固定辙叉三维瞬态滚动接触有限元模型(图2),模型整体长15 m,考虑了车轮、辙叉、扣件、一系悬挂及簧上质量,构架及以上结构部件简化为质量点并通过一系悬挂与车轴相连,且簧上质量取为12.5 t(车体轴重为25 t,轮重12.5 t)。计算模型中的一系弹簧与扣件仅考虑与动态行为相关的刚度及阻尼,扣件系统由均匀分布的离散刚度-阻尼弹簧组成(即沿x、z轴分别有7根弹簧单元且均匀分布),模型扣件刚度及阻尼分别为80 MN/m、75 kN·s/m;一系悬挂(每轴箱)刚度及阻尼分别为17 MN/m、3 kN·s/m[16]。瞬态动力学模型可基于笛卡尔坐标系描述,坐标原点位于轮轨初始接触位置,x轴为车轮运行方向,y、z轴分别代表沿辙叉垂向及横向。

图2 固定辙叉平面图及其典型截面图
为统计在使用的重载铁路车轮型面形状,利用Miniprof轮轨廓形测量仪测量了80组重载车轮型面,对实测车轮型面处理除去噪声点后,通过3次样条曲线拟合得到车轮型面轮廓线[17]。利用拟合的名义车轮型面及标准辙叉钢轨型面,建立车轮-辙叉三维轮轨瞬态滚动接触有限元模型,模型中采用过渡性网格离散,其中接触求解区最小网格单元尺寸为1 mm,模型共包含约200万个网格,由于辙叉心轨截面几何廓形沿钢轨纵向变化较快,少数截面处钢轨实体网格并不连续,采用耦合网格节点自由度的方式来保证力的传递。为精确表征车轮踏面与迎/顺车轨间的动态接触行为及辙叉轮载过渡段的受力特性,网格划分方式选用Lagrangian描述,采用库伦摩擦定律表征轮轨滚动摩擦作用,并基于罚函数的“面-面”接触算法求解时域内柔性轮轨间接触行为,摩擦系数选用0.5以模拟干摩擦环境下的轮轨相互作用。

图3 固定辙叉模型原理图及其有限元模型
模型建立过程中选用实测重载车轮型面及辙叉典型截面几何廓形图,利用Fortran语言编写程序离散轮轨几何廓形并将坐标点导入至Matlab中,结合迹线法及辙叉区轮轨接触表面坐标值确定典型断面轮轨接触状态,基于三维参数化建模软件Creo输出固定辙叉的三维实体模型(图3),并利用Hypermesh的过渡网格划分方式离散导出的实体模型,最后将离散结果导入到Ansys中,置轮轨系统于初始接触位置并对模型施加重力,获取静态轮载作用下整个模型节点的位移场(静态隐式解),将静态隐式解所求取的位移场作为初始状态,施加初始平/转动速度等初始荷载,并基于显式积分算法求取轮轨瞬态接触解。另外车辆处于牵引/制动行车方式时,可于车轴处施加牵引/制动转矩以模拟车辆起动/制动行车方式[18],使得纵向轮轨力最大可达静轮载的30%。
2 轮轨滚动接触行为分析
2.1 轮载过渡特性
为研究车辆顺/逆向过岔时的轮轨接触行为及轮载过渡段的应力、应变特性,对车轮车轴处施加牵引转矩以提供足够的牵引力作用于轮轨表面,在忽略车轮转动惯量的前提下赋予车轮转动速度。另外,计算中车辆的运营速度分别为80、100、120 km/h。

图4 心/翼轨竖向轮轨力时程曲线
图4为车辆以不同速度顺/逆向通过辙叉时的心/翼轨竖向轮轨力时程曲线,当车轮逆向通过时,翼轨上承受的轮轨力以静轮载(120 kN)为中心出现小幅波动,并随着运行时间的增加逐渐趋于平稳,由于轮轨接触状态从静态过渡到瞬态时,车轮荷载破坏了静态隐式计算所获得的对称位移场,并于初始位置(x=0)引入一个与速度相关的初始激扰,赋予的初始速度越高,激发的初始动态效应及激扰强度越剧烈,因此需要一定长度的钢轨作为动力松弛距离以保证车轮能稳定运行。
结合国内外基于图像处理和机器视觉技术进行分选现状可知,当前国内外对颗粒状农产品的分选研究已经发展较为成熟,并很多应用于实际生产中,且可以达到很高的分选精度和检测速率,但在图像处理领域还在图像分割、特征提取和图像识别方面存在着困难,在硬件上要实现实时地进行图像分割也是一个技术难点,提取何种特征最适合,采用什么样分类器,要配置什么样的处理器等等,仍需要不断进行改进技术,进一步完善。

图5 心/翼轨纵向轮轨力时程曲线
当车轮行进至轮载过渡段时,轮轨接触点于轮载转移后发生突变,荷载从翼轨逐渐向心轨过渡,翼轨所承受的轮轨力呈线性下降,同时心轨承受的轮轨力明显提升,且作用于心轨上的轮轨力于轮载过渡时达到峰值。当车轮运行至轮载过渡段后,在轮轨冲击及心轨几何廓形变化的影响下,轮轨力将呈现一定幅度的波动,且波动大小与速度呈正相关,随后其波动幅度在刚度-阻尼弹簧的作用下呈减小趋势,最终仍于静轮载(122.5 kN)左右浮动。车轮顺向过岔时轮轨力变化规律与逆向过岔存在些许差异,当轮轨接触点位于心轨上时,由于心轨截面几何廓形演变速率较快,导致轮轨力初期波动幅度相对逆向过岔时更为剧烈。车辆顺向过岔时翼轨承受的轮轨冲击力更为剧烈,作用于翼轨上的轮轨力于车轮行进至轮载过渡段后达到峰值,且轮轨力振荡幅度随着车轮在翼轨上继续向前滚动而逐渐减小。
由于道岔多铺设于车站附近,加之车轮过岔速度低于区间运行速度,因此车轮以牵引/制动行车方式下过岔的速度是可变的,图5为车轮纵向力在牵引/制动行车方式下的时程规律曲线。从图5可见,辙叉轮载过渡段纵向轮轨力衰减速度大于竖向轮轨力衰减速度,并于轮载过渡的极短时间内降低至0。另外,轮载过渡段内结构不平顺能加剧纵向力作用,且纵向力增幅分别为72%和113.3%,因此辙叉区结构不平顺所激发的纵向轮轨力增幅远大于竖向轮轨力,轨面切向力将逼近库伦摩擦力阈值,引起轮轨间黏着系数下降[19],这些必然会影响车轮荷载对辙叉的动力破坏作用,加剧辙叉钢轨轨面磨耗以及滚动接触疲劳等伤损行为的发展速率。
车轮在辙叉钢轨轨面向前滚动过程中,为进一步探明轮轨力的变化规律及轮载过渡段内轮轨接触状态的变化规律,提取心轨顶宽分别为10、20、30、50 mm下的轮轨接触状态(图6,轮轨初始位置x=0)。
从图6可知,当轮轨接触点位于辙叉咽喉至心轨开始承载断面位置前的区域时,轮轨接触点随着轨距不断加宽向车轮外侧移动,导致轮轨力出现小幅波动;当车轮滚动至轮载过渡段时,辙叉心轨开始承受车轮动载,轮轨接触点随心轨顶面的加宽和抬高而继续外移,翼轨所承受的轮载逐渐转移至心轨上,且翼轨处轮轨间接触角明显增大。当车轮前行至心轨完全承载断面位置时,车轮荷载完全转移至心轨上并由心轨独立承受,心轨处轮轨间接触角逐渐降低,轮载发生转移后,轮轨接触点从靠近轨距线附近随心轨顶宽加大而继续外移,心轨处轮轨间接触角继续降低,并诱发轮轨力出现小幅波动。
2.2 接触受力分析
辙叉心轨磨耗、轨面裂纹及叉心压塌等伤损病害是降低道岔服役寿命的关键因素之一,辙叉区轮载过渡处有害空间及结构不平顺问题将激起剧烈轮轨冲击力,导致车轮通过时会产生剧烈的振动,这是辙叉磨耗、轮轨滚动接触伤损发展速率大幅提升的主要因素[7],以车辆(100 km/h)逆向通过辙叉为例,图7为轮载过渡段内辙叉心/翼轨轨顶及截面处Mises应力、yz剪切应力分布。

图6 车辆过岔时典型轮轨接触状态
从计算结果可知,距轨顶约8 mm以下单元的Mises应力接近于屈服强度,可见辙叉心轨轨顶至轨顶下8 mm处为薄弱区。结合表1数据可知,当轮轨接触点位于咽喉区至心轨开始承载断面之间时,接触应力为955 MPa且由翼轨完全承担,当轮轨接触点位于轮载过渡区时,翼轨及心轨同时承受车轮荷载作用,翼轨所承受的应力逐渐减小且接触斑面积逐步缩小至0,而心轨轨顶处应力明显提升,由于心轨处轮轨接触半径较小,因此接触斑呈狭长状,轮载过渡区内Mises应力及yz剪切应力最值明显提升,分别为1 540、451.29 MPa。车辆过岔的完整过程中,心轨轨面接触斑面积逐渐增大并趋于稳定,且轮载过渡段内心轨轨面Mises应力呈先增大后减小最后趋于稳定的变化趋势,心轨处Mises应力最大可达1 553 MPa,远高于材料屈服强度,长期服役条件下的辙叉在车轮荷载反复作用下出现塑性变形累积,最终导致钢轨压溃伤损,加之钢轨磨耗发展速率与轮轨接触应力呈正相关[20],因此心轨在剧烈的应力场作用下易出现磨耗、压溃等伤损病害。
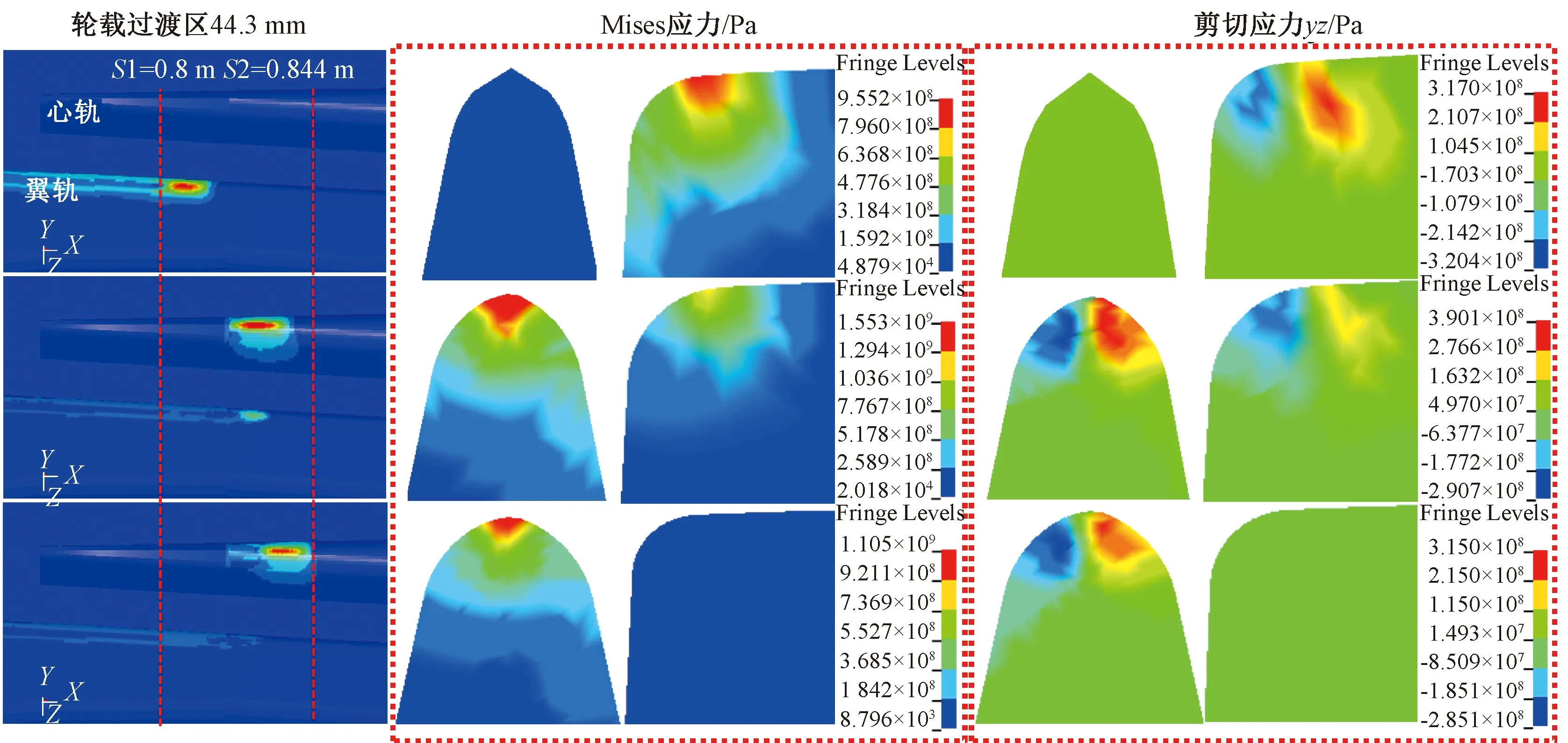
图7 轮载过渡区Mises应力及剪切应力分布
表1 轮载过渡区接触解
img id="e2f1485306ac0ce912a2cae4168b332f" class="picture_table" src="images/0ad4173eb41b3da212fef3f5b5890c7c.jpg" width="768" height="202" title="width=768,height=202,dpi=110" />
距咽喉区位置/m组件接触斑长度/mm接触斑宽度/mm接触斑面积/mm2Mises应力/MPayz剪切应力/MPa最大竖向轮轨力/kN0.800心轨000000翼轨11.44.2153.2955.21317.04112.40.811心轨6.83.268.3494.1983.1715.4翼轨10.63.8128.3868.74235.28108.70.822心轨14.84.2195.91105.41391.1495.2翼轨9.23.5101.1512.51172.7869.50.833心轨13.44.8202.01540.59451.29159.7翼轨7.83.278.4449.63124.6242.50.844心轨13.05.4220.51461.45315.24134.6翼轨000000
3 接触疲劳伤损分析
轮轨接触表面相互作用时的应力应变状态可能为弹性、弹性安定、塑性安定及棘轮效应等4种,接触载荷、材料硬化特性、接触状态的改变及残余应力是影响上述特性的关键原因[21]。在车轮荷载的反复作用下,材料内残余应力不断增加,进而促使其力学性能明显提升。如图8所示,弹性表示当车轮荷载位于弹性极限内时,结构间变形为完全弹性;弹性安定为当轮轨相互作用下的应力场提升并超过弹性极限时,初期材料表面产生塑性变形,但由于后期局部残余应力及塑性硬化的综合影响使得后续结构变形形式完全变为弹性变形,即为弹性安定;当荷载进一步增强时,会出现塑性安定及棘轮效应两种情况;塑性安定表示应力场低于材料安定极限时,塑性变形不会随循环次数的增加而增大,循环应力-应变曲线维持稳定闭合状态,因此无塑性变形的累积,即为塑性安定;棘轮效应表示荷载超过安定极限后,循环应力-应变曲线呈无法闭合状态,每次循环荷载下的塑性变形会累积,即为棘轮材料特性。棘轮效应及塑性安定是最易引起接触区域伤损的主要因素。

图8 循环荷载作用下轮轨接触区材料特性
为评价轮轨应力场作用下辙叉区滚动接触疲劳性质,结合安定图(图9)中的轮轨接触应力及牵引系数来综合评论辙叉区轮轨滚动接触疲劳,无量纲化的接触应力V为
式中:P0为最大接触应力,N/m2;K为纯剪切屈服强度,N/m2。接触班疲劳指数FIsurf为
式中:μ为牵引系数;FN为接触法向力,N;a、b为接触斑长、短半轴长度,m。WP为轮轨接触工作点,可根据牵引系数及无量纲化的接触应力来确定,根据安定理论,当轮轨接触工作点位于棘轮效应区域时(即FIsurf>0),轮轨接触表面易萌生疲劳接触裂纹。

图9 安定图
以运营速度为100 km/h的车辆过岔为例,并基于辙叉区的三维瞬态滚动接触有限元模型,获取牵引/制动行车方式下车轮和钢轨的瞬时接触行为,车轮及辙叉区钢轨硬度取为320 HB,4个典型断面下轮轨应力、应变状态在安定图上的分布如图10所示,图中①、②、③、④分别对应图6中的(a)、(b)、(c)、(d)断面。
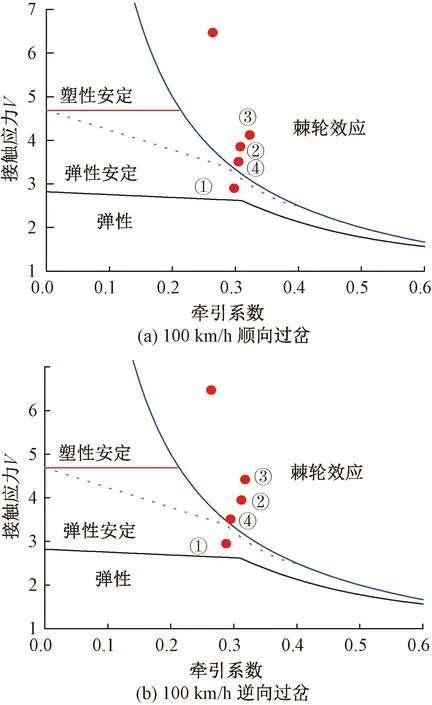
图10 不同断面下辙叉钢轨安定性分析
考虑到心轨容易产生滚动疲劳裂纹、磨耗及累计变形等伤损病害,以车辆逆向过岔为例,分别计算图6中对应位置的疲劳指数。当心轨承受车轮荷载作用时,由于变截面心轨处轮轨接触半径较小,导致辙叉心轨承受的接触应力及剪切力较大,加之心轨薄弱断面处受到轮轨冲击,所激发的轮轨高应力场将引起心轨轨面发生棘轮效应,造成轨面剪切破坏,最终引起心轨裂纹萌生,而翼轨所对应的位置为弹性安定区,处于相对安全区域,因此固定辙叉心轨为相对薄弱部件。车辆顺向过岔时,从上述分析可知,最大轮轨冲击力作用于翼轨上,心轨上承受的荷载作用于静轮载左右浮动,由于翼轨处接触半径较大,因此车辆顺向过岔时的最大无量纲接触应力反而略小于逆向过岔工况,逆向过岔比顺向过岔对辙叉的服役性能演化影响更为剧烈。
疲劳指数为工作点距棘轮效应曲线之间的水平距离,可通过描述工作点与理论效应曲线之间的距离来表征轮轨接触疲劳发生的难易程度,从图11可知,心轨断面顶宽为20~30 mm处疲劳指数大于0,峰值分别可达0.2和0.233,为易累积残余应变而产生棘轮效应的区域,随着车轮荷载的反复作用,钢轨表面材料塑性变形累积至超过材料韧性后,易导致裂纹萌生。心轨断面10、50 mm顶宽处疲劳指数小于0,因此轮载过渡段内心轨出现接触疲劳现象的概率最大,固定辙叉心轨20~30 mm断面处为相对薄弱位置。
4 结论
通过建立固定辙叉的三维瞬态滚动有限元模型,模拟车轮通过时的轮轨接触作用,可以得到以下结论:
(1) 车辆过岔时的轮轨相互作用随着速度的提升而明显增加,以车辆运营速度100 km/h为例,车辆逆向过岔时冲击心/翼轨所激发的最大轮轨力为静轮载的1.74倍,顺向过岔时翼轨承受的冲击作用比逆向过岔心轨承受的轮轨力更为剧烈。逆向过岔时心轨于轮载过渡段内出现最大荷载作用,而顺向过岔时翼轨于轮载过渡段后承受最大荷载作用。
(2) 车轮以牵引/制动行车方式通过道岔时,轮轨纵向力衰减速度快于竖向力衰减速度,且于轮载过渡段内的较短时间内降低至0,但轮载过渡结构不平顺激发的纵向力增幅大于竖向轮轨力,纵向力逼近库伦摩擦力阈值,进而导致轮轨间黏着系数降低,必然会影响列车过岔的安全性和平稳性。
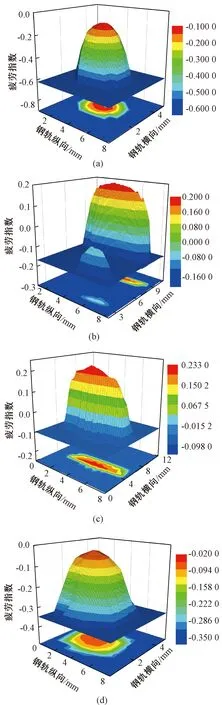
图11 接触斑疲劳指数三维图
(3) 车辆逆向过岔时,在轮载过渡段范围内,变截面心轨所承受的Mises应力呈先增加后减小趋势,心轨轨面处接触应力先增大后减小最后趋于稳定。距心轨轨顶约8 mm以内的区域存在较强的应力场作用,此区域为裂纹、磨耗等伤损劣化萌生的高危区域,这与固定辙叉现场伤损的发生情况一致。
(4) 根据轮轨接触表面在相互作用时的应力/应变状态可知,车辆逆向过岔时,翼轨承受车轮荷载作用下的工作点位于弹性安定区域,为相对安全区域,且接触斑疲劳指数小于0;心轨承受车轮荷载作用下的工作点处于棘轮效应区域,接触斑疲劳指数大于0,为易引起接触疲劳的区域,因此固定辙叉心轨20~30 mm断面处为相对薄弱位置。而车辆顺向过岔时的无量纲接触应力小于逆向过岔工况,逆向过岔比顺向过岔对辙叉的服役性能演化影响更为剧烈。
本文研究工作发展了三维轮轨瞬态滚动接触有限元模型,数值再现了重载线路车轮与辙叉间复杂的瞬态滚动接触行为,能够为探明固定辙叉轮载过渡区间内轮轨接触行为及伤损特性分析提供基础,后续将开展固定辙叉的现场跟踪测试,利用力锤实验验证所建模型的精确性,为固定辙叉养护维修及结构优化提供理论支撑。
