隧道近接施工对上部既有重载铁路隧道安全稳定性影响研究

王海龙，董 捷，武志辉，王志岗

(1.河北建筑工程学院 土木工程学院，河北 张家口 075000; 2.河北省土木工程诊断、改造与抗灾重点实验室，河北 张家口 075000)

随着我国交通线网密度的逐年增加，各类高风险交叉隧道工程逐年增多。其中，小净距重载铁路交叉隧道因上部重载列车轴重大、荷载持续时间长、冲击荷载幅值高等因素的影响，交叉段下部新建隧道施工给上部既有重载铁路安全运营带来极大风险。

众多学者针对地铁列车运行引起隧道结构的动力响应规律进行了研究。文献[1]基于有限元数值方法，针对地铁振动荷载作用下近距离平行隧道结构的二维弹塑性动力响应进行模拟，分析隧道结构体系的加速度和内力响应特性。文献[2-3]通过建立交叠隧道三维计算模型，分析了地铁列车荷载作用下的隧道结构振动响应及其频谱特性。文献[4]建立车辆-轮轨模型，研究地铁运营期间列车振动荷载对隧道衬砌结构变形及内应力的影响。文献[5-8]结合二维或三维数值模拟结果，研究列车振动荷载作用下隧道结构的动力响应规律。

文献[9]针对普通铁路隧道，以隧道立体交叉工程为背景，通过数值模拟方法，开展列车动荷载作用下不同立体交叉结构位移、加速度、内力响应规律的研究。文献[10]利用分层法研究了列车移动荷载作用下隧道交叉断面处隧道结构及围岩振速与动位移的响应规律。采用列车激振力函数模拟高速列车竖向荷载，运用弹塑性有限元方法及数值模拟对大断面隧道结构[11]、交叉隧道结构[12]在列车振动荷载作用下的动力响应进行了深入的分析。文献[13-14]以列车振动荷载现场测试成果为基础，获得隧道衬砌结构竖向位移、竖向加速度的响应特性。

相比而言，重载列车激励荷载作用下铁路隧道结构的动力响应研究较少。文献[15]将基底填充层表面实测加速度时程曲线作为激振荷载，运用Ansys软件进行重载列车作用下隧道结构的动应力分析。针对重载铁路隧道基底结构受列车荷载作用更大的特点，部分学者结合现场试验和数值模拟，研究重载列车荷载作用下铁路隧道基底结构的位移、加速度[16]、动压力[17]及动应力分布特点[18]。

总结发现，以往研究内容多涉及地铁或山区普通铁路交叉隧道，而下穿隧道近接施工过程中，受上部隧道重载列车荷载的影响，交叉段围岩受力状态、既有隧道沉降变形及动力响应特性将异常复杂。基于此，本文以新建京张高速铁路草帽山隧道下穿唐呼重载铁路北草帽山隧道为例，重点研究下穿隧道施工及列车荷载作用下既有隧道衬砌结构沉降变形及动力响应特性，从而为类似重载铁路交叉隧道工程提供技术支持及经验参考。

1 现场测试

1.1 工程背景

新建京张高速铁路草帽山隧道位于河北省张家口市沙岭子镇北，隧道采用单洞双线形式，隧道进口里程DK172+980，出口里程DK180+320，全长7 340 m，设计速度250 km/h。

隧道在DK173+862—DK174+057段下穿唐呼铁路，京张高速铁路草帽山隧道与唐呼铁路北草帽山隧道交接里程DK173+965(唐呼铁路IDK25+620)，见图1。相交段京张高速铁路草帽山隧道设计为Ⅲ级围岩，唐呼铁路北草帽山隧道为Ⅴ级围岩，隧道周边为凝灰岩、凝灰质熔岩，强风化，岩石裂隙发育，气孔发育，呈散体状结构。新建隧道拱顶距唐呼铁路隧道底约16.39 m，隧道平面交角76°，该隧道底层为全强风化凝灰岩。为保证隧道施工顺利进行和唐呼铁路运营安全，隧道下穿唐呼铁路段施工以“预加固，短进尺，弱爆破，强支护，早封闭，勤量测”的原则进行。

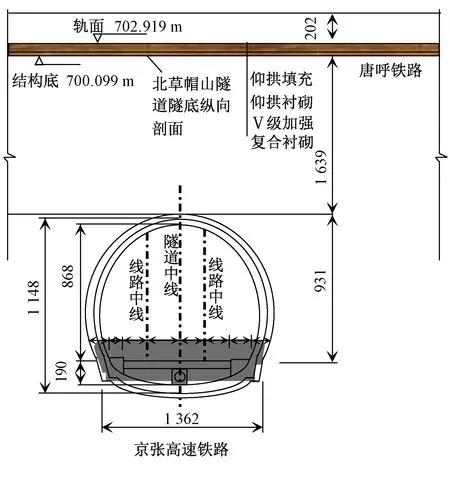
图1 交叉隧道示意(单位：mm)

1.2 测试概况

振动测试采用TC-4850N高精度测振仪，内置4G和WIFI网络传输模块，可以将传感器采集到的衬砌结构振动数据传到互联网专用服务器上，并与4850N-Software结合实现动态数据的处理。沉降监测元件采用精度为0.001 mm的液压式静力水准仪(PT124B-226)，设置自动采样频率5 min一次，现场监测示意见图2。

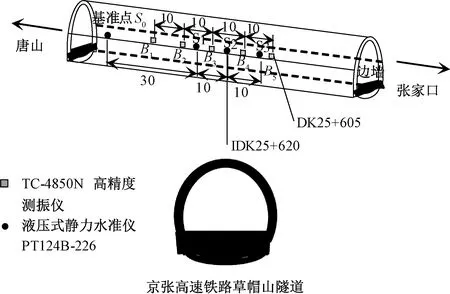
图2 既有隧道监测点布设(单位：m)

2 重载列车振动荷载模拟

重载列车作用于轨道上的轮轨作用力主要由两部分组成，一部分是列车自重产生的静载，另一部分是列车运行产生的振动荷载。目前，在列车荷载模拟研究过程中，文献[19]采用解析法建立了轨道结构耦合分析模型，用移动常荷载或移动简谐荷载模拟地铁列车。文献[20]建立车-轨-隧道-地基竖向耦合动力模型，计算列车荷载作用下轨道道床接触点荷载时程。大多学者[2,6,9,11,21-22]主要采用激励力函数来模拟地铁及高速列车荷载，该函数数定表达式为

F(t)=k1k2(P0+P1sinω1t+P2sinω2t+P3sinω3t)

( 1 )

式中：k1为相邻轮轨力叠加系数，取值为1.2～1.7；k2为钢轨分散系数，取值为0.6～0.9；P0为列车静载。

Pi=M0aiωi2

( 2 )

式中：M0为列车簧下质量；ai为轨道几何不平顺控制条件的矢高；ωi为轨道不平顺控制条件下的振动圆频率，表达式为ωi=2πv/Li，v为列车速度，Li为几何不平顺曲线的典型波长，具体见文献[6,9]中引用的英国铁路中心轨道几何不平顺控制值。

目前普通列车或高速列车振动荷载谱大多采用该经验公式数定模拟，部分学者[18,23-24]采用激振力函数来模拟重载列车振动荷载。研究发现，选用该模型模拟重载列车荷载时并不完全适用。例如，满载C80B重载列车，单边轴重12.5 t，簧下质量约为2 t，得到该重载列车以80 km/h速度行驶时的振动荷载波形，见图3。

图3 列车荷载模拟时程

该模型中列车动荷载波动幅值较小，最大值约165 kN，最小值约110 kN，即列车运行过程中，轨道结构时刻承受着来自列车的激励荷载。该模型忽略了车厢转向架间轴距对列车附加振动荷载的影响。中国铁道科学研究院经过大量的实测分析认为，列车荷载直接由轮下的一根轨枕和前后各两根轨枕共同承担，相应的分担比为0.1∶0.2∶0.4∶0.2∶0.1[25]。因此，在列车行驶过程中，位于每节车厢正下方的部分轨枕将不受列车轮载作用，即该时刻部分轨枕受到的列车振动荷载基本为0，与目前列车荷载数定模型有一定偏差，可见该模型不能完全适用于重载列车动力荷载的模拟。

当列车在隧道内运行时会产生振动，振动经轨道结构传递到轨枕等支承结构上，通过道床表层再以波的形式经由隧道衬砌结构向周边传播，引起衬砌结构及围岩振动。为了分析列车-轨道-道床竖向振动特性，计算轨枕传递给道床表层的动荷载，采用图4所示的振动分析模型。

图4 轨道振动荷载分析模型

该动力分析模型是由列车、轨道、道床耦合组成的，基于既有列车振动荷载数定模型，充分考虑重载C80B列车轴重、车速及编组的影响，结合轮下轨枕对列车振动荷载的有效承担比，并参考文献[18,26]中重载铁路激励荷载幅值，修正后的满载C80B列车振动荷载模拟波形见图5。

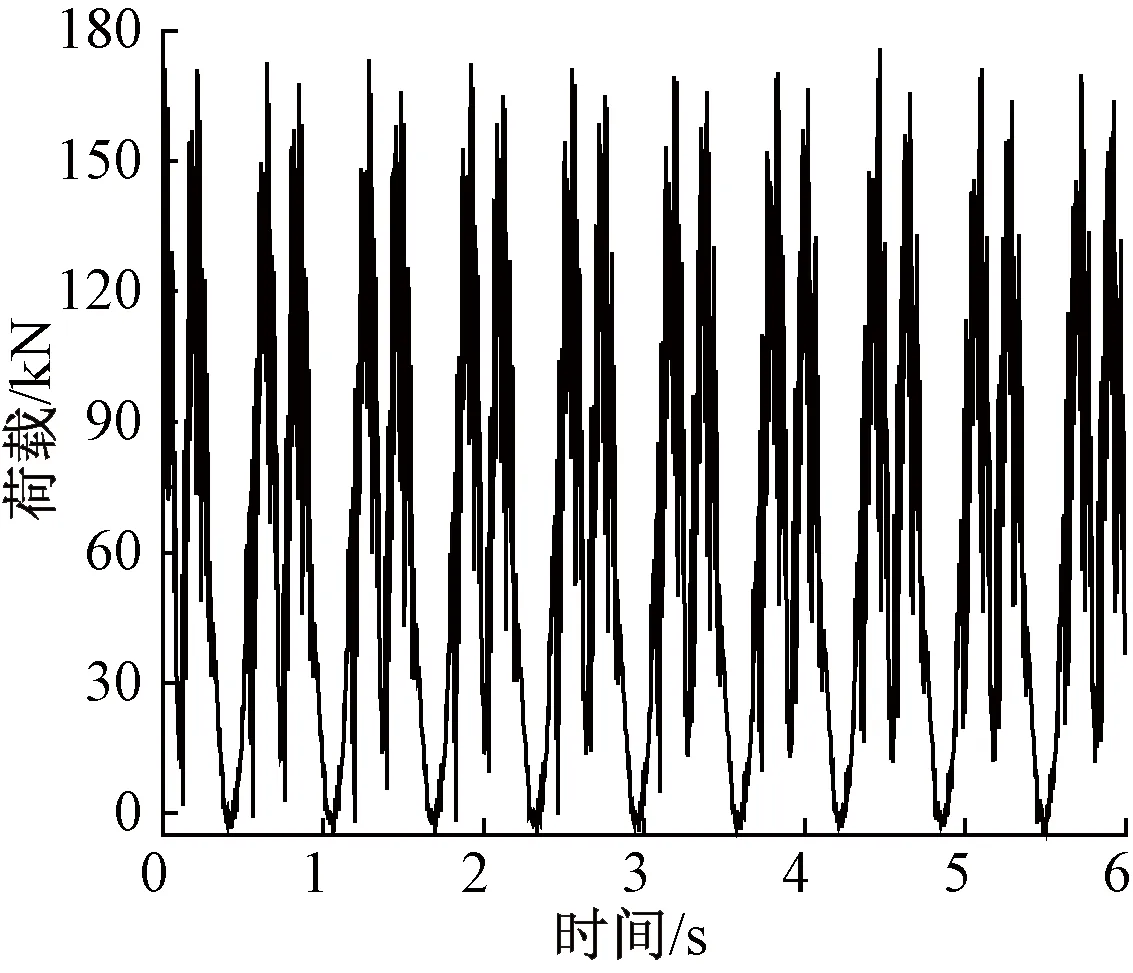
图5 重载列车激励荷载修正时程

在数值计算过程中，可将每根轨枕处道砟层振动荷载作为激励振源，本次数值模拟振源选取修正的重载列车荷载时程，见图5。

3 数值模拟

3.1 数值模型建立

以京张高速铁路草帽山隧道下穿唐呼铁路北草帽山隧道交叉段为分析对象，分别建立全断面法、台阶法及三台阶开挖施工动力分析模型，具体开挖工法如下。距离为负值表示近接交叉断面施工开挖，正值表示远离交叉断面施工开挖。

(1)全断面法开挖：掌子面施工至距交叉点0、±6、±13、±20、±30、±50 m。

(2)台阶法开挖：台阶长度10 m，上下台阶高度分别为6.5 m和5.5 m，上台阶掌子面施工至距交叉点0、±6、±13、±20、±30、±50 m。

(3)三台阶法开挖：台阶长度6 m，上台阶高度取2.5 m，中台阶和下台阶高度取3.5 m，仰拱滞后下台阶8 m后闭合，上台阶掌子面施工至距交叉点0、±6、±13、±20、±30、±50 m。

为了提高动力计算效率，减少动力计算时间，锚杆对围岩的加强作用通过提高锚固区围岩的力学参数进行模拟，提高锚固区围岩弹性模量、黏聚力及内摩擦角约1.3倍可较好模拟锚杆作用[27-28]。在静力分析阶段，模型四周边界约束法向位移，模型底部设为固定约束，上表面为自由面；动力分析过程中，模型四周及底部设置静态边界，可有效吸收模型边界处的入射波，从而减少入射波在模型边界处的反射，提高数值分析的准确性。

静态边界条件使用阻尼器来消耗边界法向和切向的能量，阻尼器提供的法向和切向黏性力分别为tn、ts,计算式为

tn=-ρCpvnts=-ρCsvs

( 3 )

( 4 )

式中：ρ为岩土体密度；Cp为压缩波波速；Cs为剪切波波速；vn、vs分别为边界处法向速度、切向速度，模型动力求解过程中，其值依据相邻实体单元网格节点速度值计算，分别为边界网格节点速度的法向分量及切向分量，且模型计算过程中随着节点速度不断变化而变化。

交叉隧道三维模型中，下部隧道拱顶与上部隧道拱底间净距约16 m，以隧道交叉点为中心，沿隧道前后、左右各取50 m，其中上部隧道拱顶距模型上部边界30 m，向下取距离新建隧道仰拱底20 m，选取既有隧道衬砌结构拱顶、边墙及隧底三个点作为特征点进行分析，数值计算模型及监测特征点见图6。

交叉隧道围岩采用Mohr-Coulomb模型模拟，隧道衬砌结构采用弹性本构模型，围岩和衬砌结构均采用实体单元模拟。模型采用瑞利阻尼，由于岩土体材料进入塑性流动阶段时大量能量得以消耗，对于许多牵涉大变形的动力分析来说，最小临界阻尼比ξmin取0.5%就能满足要求，同时最小中心频率ωmin近似取为模型的自振频率2.0 Hz。模型分析中衬砌结构及围岩按连续、均匀介质考虑，结合京张高速铁路草帽山隧道隧道与唐呼铁路北草帽山隧道衬砌支护参数，根据隧道交叉段实际围岩级别及特性，并参考TB 10003—2016《铁路隧道设计规范》得到模型具体计算参数，如表1所示。

表1 数值模型计算参数

3.2 数值模型有效性验证

模型计算过程监测既有隧道衬砌结构边墙处沉降值和振速随下穿隧道采用三台阶法近接施工的变化情况，并与现场实际监控量测数据进行对比分析，以验证数值计算模型研究的可靠性。

现场对既有唐呼重载铁路北草帽山隧道交叉点断面(IDK25+620)进行沉降与振动监测，见图7。隧道交叉段施工期间，唐呼重载铁路北草帽山隧道C80列车运行速度约为80 km/h，重点监测列车正常运行过程中，上部隧道衬砌结构振速随下穿隧道开挖掘进的变化情况，并实时统计既有隧道沉降随下穿隧道掌子面距交叉点不同距离的变化幅值，具体统计结果见图8。

图7 沉降及振动监测示意

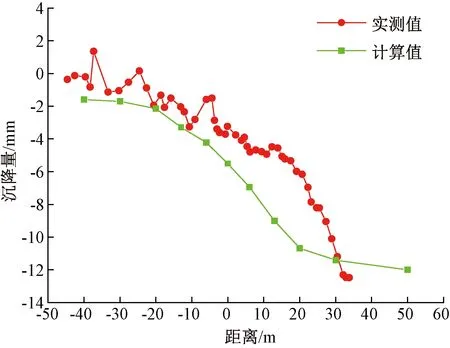
图8 既有隧道沉降曲线对比

由图8可知，数值计算模型中交叉点处沉降变形规律与实际测量情况基本一致，数值计算结果与现场测量结果差异较小。

通过对大量现场测试数据进行归纳整理，得到列车运行过程中交叉点处既有隧道衬砌结构边墙振速响应值，包括x方向(平行于隧道)振速、y方向(垂直于隧道)振速和z方向(铅垂向)振速，并与数值计算结果对比分析,见图9。

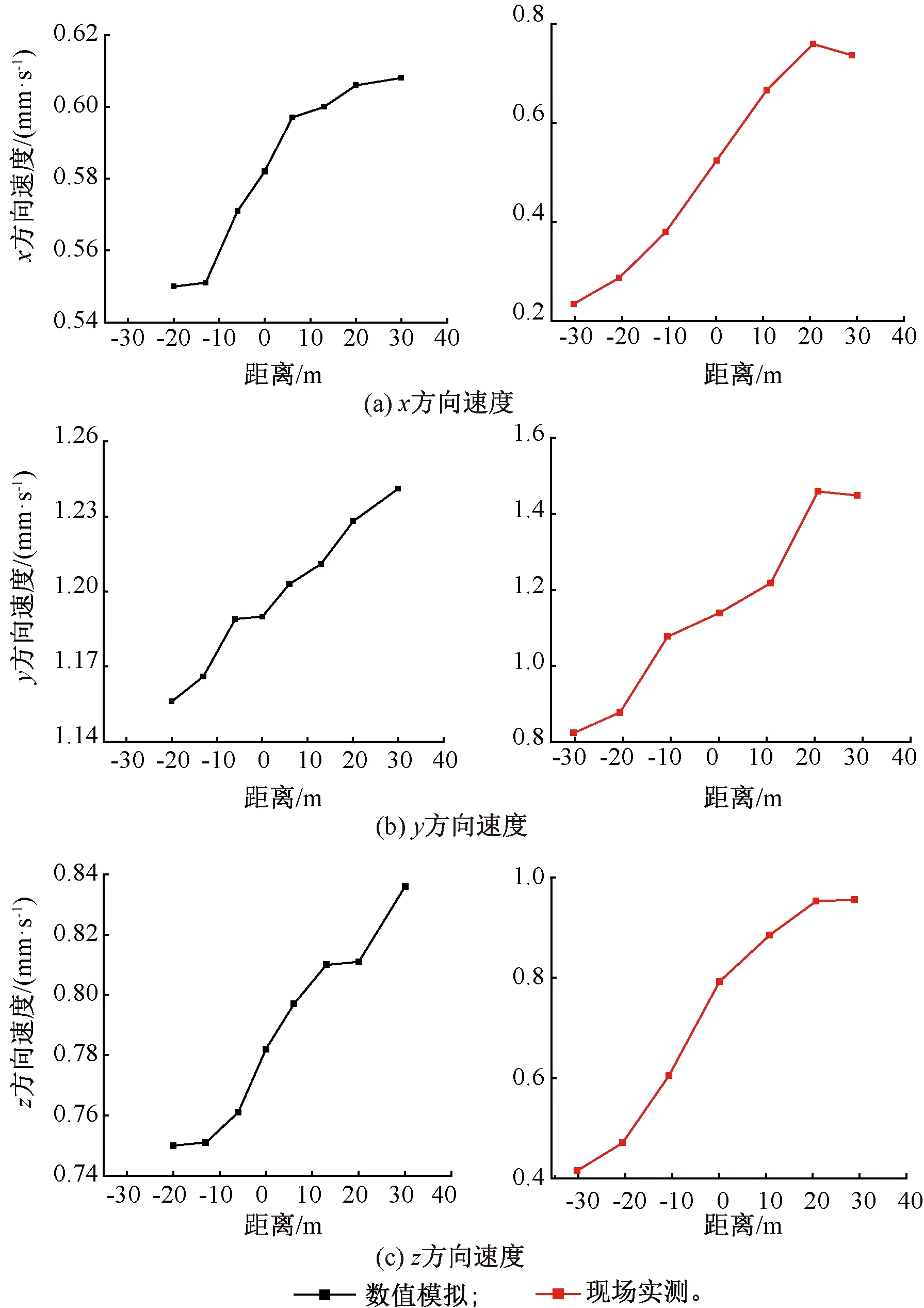
图9 既有隧道衬砌结构振速对比

由图9可知，在既有重载铁路正常运营条件下，随着下穿隧道掌子面的不断向前推进，从现场实测数据可以看出，既有隧道衬砌结构x方向振速为0.235～0.736 mm/s，y方向振速为0.823～1.448 mm/s，z方向振速为0.415～0.956 mm/s；而后续数值计算结果显示，衬砌结构x方向振速为0.55～0.61 mm/s，y方向振速为1.156～1.243 mm/s，z方向振速为0.75～0.84 mm/s。计算结果与实测数据均反映既有隧道衬砌结构x、y与z三个方向的振速随着下穿隧道的开挖而逐渐增大，且数值计算结果与现场实测结果较为接近，验证了采用数值计算方法进行研究的可行性，从而为后续研究奠定了可靠的基础。

3.3 沉降变形结果分析

下穿隧道施工过程中既有隧道衬砌结构位移变化情况是分析隧道稳定性的重要依据，针对下穿隧道三种不同施工方法，分析既有隧道衬砌结构特征点沉降变形随下穿隧道近接施工的变化规律，沉降变形曲线见图10。

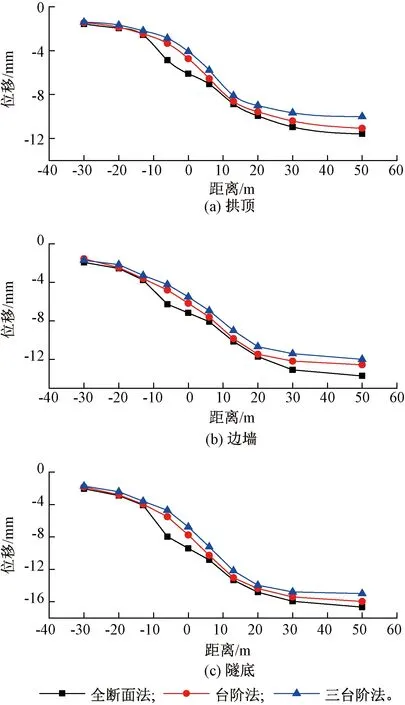
图10 既有隧道衬砌结构沉降变形曲线

由图10可知，下穿隧道采用三种不同施工方法开挖，既有隧道衬砌结构拱顶、边墙及隧底的沉降变化规律基本一致，沉降值在下穿隧道掌子面距交叉点-30～ -20 m时缓慢变化；当掌子面距交叉点-20 m时，随着掌子面的不断向前推进，既有隧道沉降趋势逐渐增大，由于下穿隧道的开挖破坏了原岩的应力平衡状态，导致岩体释放大量的能量，进一步造成围岩的破坏，于是下穿隧道开挖对既有隧道沉降影响较大；当掌子面远离交叉点30 m后，沉降逐渐趋于稳定，下穿隧道开挖卸荷对既有隧道的沉降影响逐渐减弱。其中，既有隧道交叉断面处各特征点竖向位移均表现为隧底最大，边墙次之，拱顶最小。采用三台阶法开挖引起既有隧道沉降变形值最小，隧底沉降值约为14.9 mm，台阶法约为15.9 mm，采用全断面开挖引起的沉降值最大，约为16.7 mm。显然下穿隧道开挖卸载速度会影响交叉段岩体的力学特性，从而造成上部既有隧道不同的沉降量，由于三台阶开挖的卸载速度在三种施工方法中最慢，所以对既有隧道的影响最小。

新建隧道下穿既有重载铁路隧道，实际两隧道间围岩夹层厚度为新建隧道跨度的1.1倍，分别以围岩夹层厚度取0.5B、1.1B、1.5B、2.0B(B为新建隧道洞跨)进行研究分析，图11为交叉隧道围岩夹层不同厚度对既有隧道交叉段整体沉降变形的影响规律。

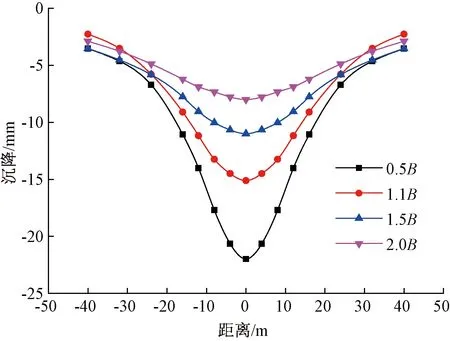
图11 隧道交叉段整体沉降曲线

由图11可知，既有隧道沉降值随着围岩夹层厚度的增加而减小。当夹层厚度为2.0B时，既有隧道最终沉降量为7.99 mm；当夹层厚度减小为1.5B、1.1B、0.5B时，沉降量分别增至10.9、15.1、21.9 mm。分析可知，当夹层厚度大于1.1B时，既有隧道沉降值随夹层厚度的变化基本呈线性关系。随着夹层厚度的不断减小，沉降量明显增大，变形发生突变，表明既有隧道结构进入破坏状态，应采取相应的加固措施。通过对既有隧道沉降量随夹层厚度变化的分析可知，新建隧道下穿既有重载铁路隧道的最小安全距离约为1.0B的范围，当隧道净距小于该范围时，新建下穿隧道施工过程中，必须采取相应的措施，确保既有隧道的安全运营及新建隧道的正常施工。

3.4 振动速度结果分析

下穿段隧道采用三台阶法开挖尽可能减轻对围岩及既有隧道的振动，下穿隧道爆破施工过程中，既有隧道衬砌结构振速容许值为2.5 cm/s，隧道施工采用光面爆破技术进行爆破作业。根据围岩情况，及时修正爆破参数，最大循环进尺为1.5～2 m，并相应调整最大装药量，以达到最佳爆破效果。爆破采用非电毫秒雷管起爆系统，引爆采用电雷管，炸药采用2号岩石乳化炸药，选用φ32药卷。

由于上台阶隧道掌子面爆破产生振动最大，重点选取上台阶爆破既有隧道衬砌结构振动监测数据与重载列车车致振动结果进行对比分析。下穿隧道爆破掘进期间所引起的上跨既有隧道衬砌振动速度值如表2所示。随着掌子面逐渐远离交叉点，测点与爆源间距离逐渐增大，施工爆破对既有隧道振动影响逐渐减弱，相比而言，重载列车引起既有隧道衬砌结构振速幅值却逐渐增大。隧道爆破施工对既有隧道产生的影响具有瞬时性，且持续时间较短，而重载列车通过隧道引起振动的持续时间相对较长，对既有隧道衬砌结构安全稳定性造成较大影响。因此，基于重载列车荷载激励，重点展开对下穿隧道施工过程中既有隧道衬砌结构振动响应特性的研究。

表2 既有隧道振速对比分析

针对下穿隧道的三种不同施工方法，通过对比分析既有隧道衬砌结构特征点振速随下穿隧道开挖步的变化情况，探究重载列车振动荷载作用下不同施工方案对上部既有隧道衬砌结构动力响应的影响规律。

图12为下穿隧道采用三台阶法开挖，在重载列车振动荷载作用下，上部既有隧道衬砌结构边墙处x、y和z三个方向振速时程曲线。

图12 既有隧道边墙振速时程图

受重载列车激励荷载的影响，衬砌结构振速迅速增大至峰值，然后趋于稳定，随着列车荷载施加结束，振速逐渐趋于0。其中，x方向振速峰值为0.6 mm/s，y方向振速峰值为1.2 mm/s，z方向振速峰值为0.8 mm/s。由此可知，在列车激励荷载作用下，交叉断面边墙振速峰值由大到小依次为：y方向、z方向、x方向。

图13反映了既有隧道衬砌结构边墙处振速大小随下穿隧道开挖的变化情况。

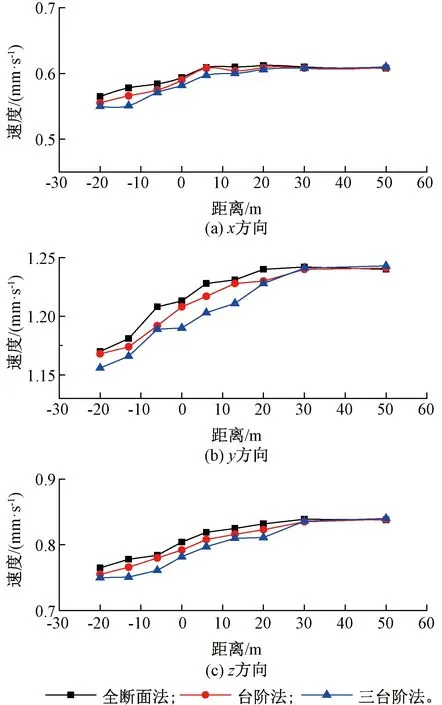
图13 既有隧道边墙振速对比

由图13可知，新建隧道采用三种不同施工方法开挖，当下穿隧道掌子面开挖至距交叉点-20 m附近时，x、y和z方向振速分别为0.55、1.156、0.75 mm/s，随着掌子面的不断向前推进，边墙处振速值逐渐增大；在下穿隧道掌子面远离交叉点30 m后，三方向振速分别为0.608、1.241、0.836 mm/s，相比分别提高10.5%、7.3%、11.5%；掌子面远离交叉点30 m后，既有隧道衬砌结构振动受下穿隧道开挖的影响较小，衬砌结构振速基本趋于一致。其中，相比于台阶法及全断面法开挖，下穿隧道采用三台阶法开挖时，既有隧道衬砌结构振速响应最小。

3.5 振动加速度结果分析

以下穿隧道采用三台阶法施工为研究对象，分析既有隧道衬砌结构不同监测部位加速度响应情况(图14)。

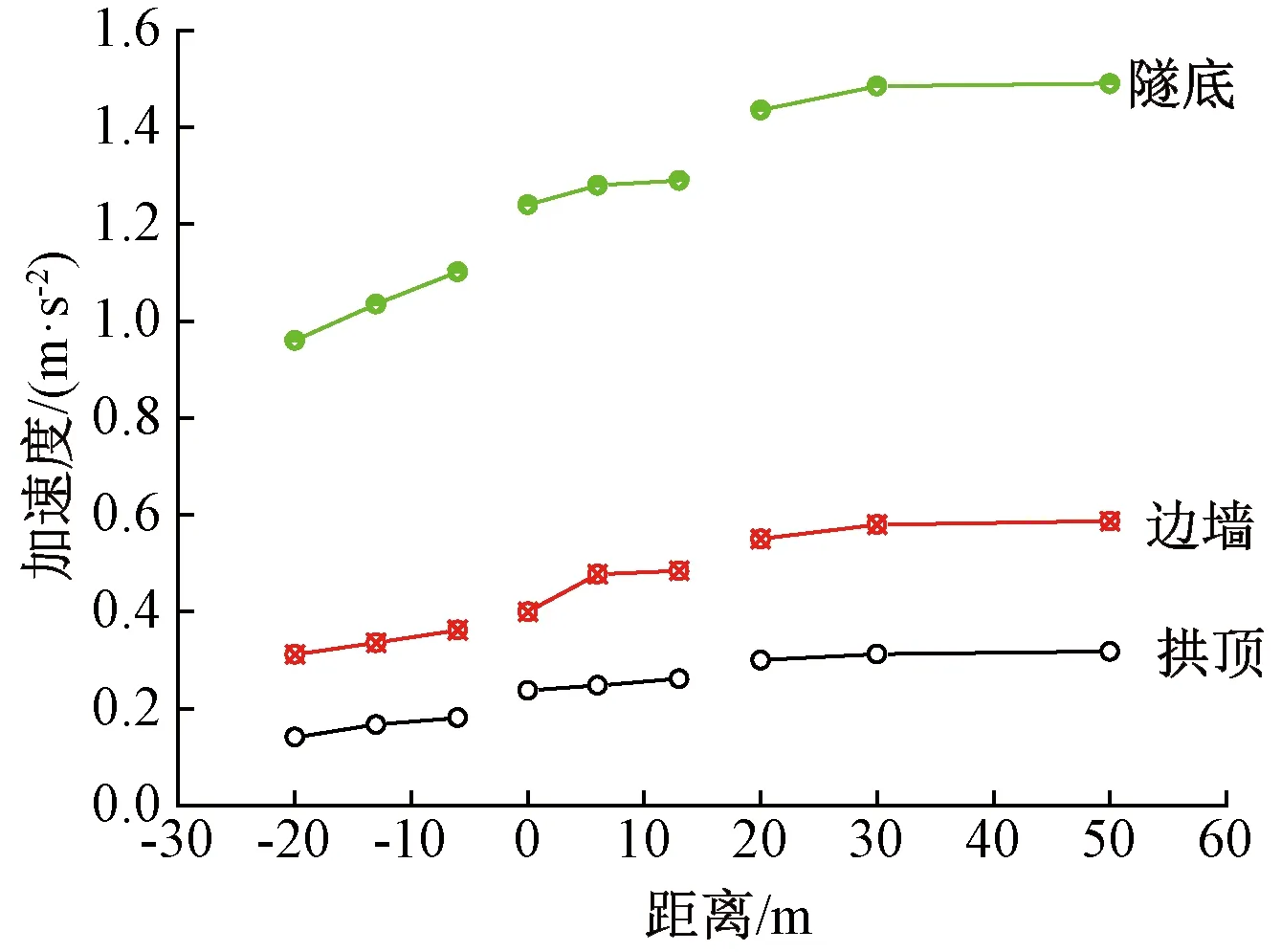
图14 既有隧道衬砌结构振动加速度

由图14可知，受重载列车激励荷载的影响，随着下穿隧道的开挖，既有隧道衬砌结构振动加速度逐渐增大，振动加速度响应表现为隧底最大，边墙次之，拱顶最小。

分别以轴重21、25、27、30 t为列车荷载激励，其中普通铁路列车轴重约为21 t[29]，选取既有隧道隧底加速度响应为研究对象，对比分析不同列车轴重对隧道衬砌结构振动加速度的影响规律，见图15。

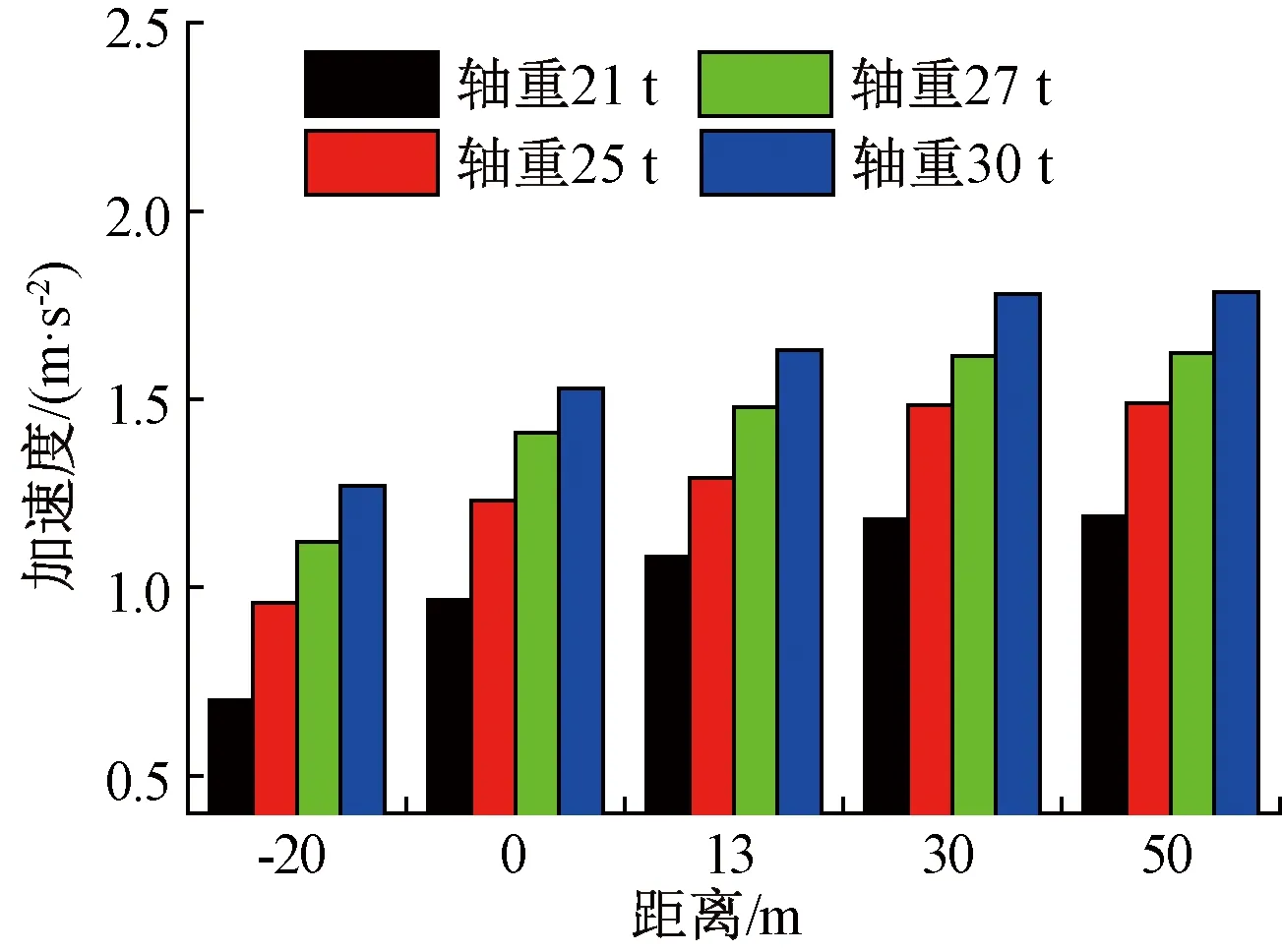
图15 不同轴重列车荷载激励下振动加速度对比

由图15可知，受列车激励荷载的影响，随着列车轴重的不断增加，隧底振动加速度幅值明显增大，重载列车引起的振动响应幅值明显大于普通铁路列车。当下穿隧道掌子面远离交叉断面50 m时，普通铁路列车引起的加速度为1.19 m/s2，重载列车轴重分别为25、27、30 t时，相应的加速度幅值分别为1.49、1.62、1.78 m/s2，与普通列车相比，加速度分别提高了25.2%、36.1%、49.0%。

综合数值计算中既有隧道衬砌结构振动加速度及振速的变化规律可知，可能由于上部既有隧道重载列车激励荷载、下穿隧道的开挖卸荷耦合作用的影响，导致隧道交叉段夹层岩体内微裂隙起裂、传播和连接贯通，造成岩石强度的降低，并进一步减小了交叉段岩体的刚度，所以重载列车行驶过程中，振动波在夹层岩体中反射强度逐渐增大。因此，在重载列车荷载作用下，上部隧道衬砌结构的振动强度随着下穿隧道的逐渐开挖而增强。

4 结论

以新建京张高速铁路草帽山隧道下穿既有唐呼重载铁路北草帽山隧道为工程背景，建立基于修正重载列车振动荷载输入的隧道近接施工三维动力仿真模型，并结合现场监控量测，对比研究了不同施工方法、不同夹层厚度、不同列车轴重对既有隧道衬砌结构沉降变形及动力响应的影响，主要结论如下：

(1)相比于全断面法和台阶法开挖，下穿隧道采用三台阶法开挖引起既有隧道沉降值较小；新建隧道下穿既有重载铁路隧道的最小安全距离约为1.0B的范围，下穿隧道掌子面距交叉点约30 m范围内，既有隧道沉降受新建隧道施工影响较大。

(2)综合数值计算结果及现场监控量测数据可知，受重载列车激励荷载的影响，既有隧道衬砌结构边墙处y方向(垂直于隧道)振速较大，z方向(铅垂向)次之，x方向(平行于隧道)振速最小；随着下穿隧道掌子面的不断向前推进，边墙处振速值逐渐增大；掌子面远离交叉点30 m后，既有隧道振速受下穿隧道开挖的影响逐渐减小。

(3)重载列车激励荷载作用下，既有隧道衬砌结构交叉断面处振动加速度响应表现为隧底最大，边墙次之，拱顶最小。随着列车轴重增大，振动加速度幅值明显增大，与普通铁路列车相比，重载列车引起的振动响应幅值明显增大，加速度最大增幅约为49.0%。