横风环境下跨海大桥列车-桥梁系统耦合振动仿真研究

崔圣爱,刘 品, 晏先娇,符 飞, 祝 兵

(西南交通大学 土木工程学院，四川 成都 610031)

列车在横风环境中运行时 其气动特性会发生明显变化，使气动荷载和车辆轮轨接触力显著改变，造成横摆超限、脱轨，甚至出现翻车和人员伤亡事故。特别是在大跨度桥梁上运行时，气动力的改变更加显著，且大跨度桥梁结构轻柔，列车通过时的耦合振动问题比较突出，脱轨和倾覆的几率进一步增大[1]。横风作用下列车与桥梁的耦合振动问题备受关注，不少学者对列车-桥梁系统在风荷载作用下的动力响应及列车运行安全性进行研究，取得了一系列的研究成果。西冈隆等[2]较早关注列车上的风荷载作用，将风荷载均布于列车上，开展了桥梁上车辆的动力响应研究。Diana等[3]研究了列车在平均风荷载作用下通过桥梁时的动力响应。郭向荣等[4]通过时域分析法，利用横向脉动风场并考虑纵桥向的空间相关性，分析了斜拉桥上列车高速通过时的动力响应。葛玉梅等[5-6]考虑了静风荷载和脉动风荷载作用，基于节段模型桥梁风洞试验，结合列车和桥梁互相的气动作用影响，根据三分力系数以及Scanlan的准定常表达，采用时域积分法以斜拉桥为研究对象，分析了风荷载作用下车-桥耦合动力响应。夏禾、郭薇薇和徐幼麟等[7-13]基于模拟的脉动风速场，采用模态综合法以青马大桥和武汉天兴州大桥等斜拉桥和悬索桥为研究对象，分析计算了列车和风荷载同时作用下的动力响应规律。李永乐等[14-18]综合分析了列车和桥梁气动力的相互影响，研发出一套协调考虑风-车-桥相互作用的交叉滑槽测试装置，并将运动列车模拟对气动荷载的影响通过余弦准则和定常假设进行考虑，构建了一套比较完备的风-车-桥非线性系统空间耦合分析模型，并利用该模型系统地对风场特性、列车位置和速度以及风速进行了多参数研究。

显然，基于传统动力学分析的车辆建模方法严重依赖于系统构型，一旦系统或自由度改变，动力学方程需重新建立。多体系统动力学方法则可以实现程式化的建模，并被认为是车辆动力学得到突破性进展的有力证明。计算流体力学通过数值求解控制流体流动的微分方程，获得流体流动的流场在连续区域上的离散分布，模拟流体流动情况。随着数值分析技术与传统动力学的不断融合，将多体系统动力学、有限元以及计算流体力学结合起来，构建横风作用下高速铁路车桥动力学分析平台，是不同力学领域交叉学科研究的重要方法。横风环境下跨海大桥列车-桥梁系统耦合振动的仿真研究，涉及三个领域，分别是风荷载、包括复杂轮轨关系的列车及桥梁，它们可以分别通过计算流体力学软件(Fluent)、多体系统动力学软件(Simpack)及有限元软件(Ansys)独立求解。然后基于各初始值，在多体系统程序中进行联合仿真。

平潭海峡大桥全长11.15 km，是长乐至平潭和福州至平潭间的高速公路和铁路上的一个关键性控制工程，是我国第一座真正意义上的公铁两用跨海大桥，桥址区设计风速为44.8 m/s，风力较强，列车运行安全性难以保证。本文选用CRH3型高速列车，以平潭海峡的大小练岛水道斜拉桥作为工程对象，建立列车和桥梁的气动模型和车-桥系统多体动力学模型。针对双线会车情况，仿真计算横风作用下列车-桥梁系统的气动荷载和动力响应。研究基于风速、车速不同组合工况下列车和桥梁各动力学指标的变化规律，并给出各风速下车速的建议限值。

图1 弹性体在多体系统中的动力学描述

1 弹性体在多体系统中的耦合集成

弹性体在多体系统中的运动学描述如图1所示,任意点P的运动可描述为

rP=r(t)+c+u(c,t)

(1)

式中：r(t)和c为刚体运动矢量；u(c,t)为变形矢量，其Ritz近似为

(2)

式(2)为模态振型uj(c)与其相应的依时间变化的模态坐标qj(t)加权的线性组合。

此外，应变可通过线性应变-位移关系表示为

ε(c,t)=Dεuu(c,t)

(3)

式中：Dεu为微分算子。应力则可通过线弹性材料定律得

σ(c,t)=Hε(c,t)

(4)

式中：H为弹性矩阵。为建立弹性体的运动方程,将式(4)代入到式(1)，并利用虚功原理得

(5)

其中，ρ为质量密度；p为外力。

从而得到在多体系统(MBS)中弹性体的运动方程。从式(5)中提出依时间变化的变量后，得

(6)

弹性体在多体系统中的详细计算方法参见文献[19-21]。

2 横风环境中列车-桥梁系统气动荷载

2.1 计算模型

平潭海峡大小练岛水道大桥跨径组合为80 m+140 m+336 m+140 m+80 m(如图2所示)，为公铁两用斜拉桥，钢桁主梁为倒梯形断面，尺寸如图3所示。列车模型采用CRH3型高速列车，列车实际长度较长，文中保持列车中部截面不变，采用3节编组的列车进行模拟。列车高度为3.89 m，宽度为3.257 m，列车的头、中、尾车长度分别为25.6、24.2、25.6 m。

图2 桥梁总体布置图(单位：m)

图3 主梁断面图(单位：m)

为模拟列车实时运动，结合动网格和滑移网格的优点，采用局部动态层网格进行建模。网格分区示意如图4所示。

计算域入口边界设为速度入口，采用指数型风剖面，横风沿高度的分布规律为

(7)

计算域出口边界设为压力出口，计算域顶面设为对称边界，移动区域与固定区域的相交面以及两个移动区域间的相交面均设为交界面，列车、桥梁表面和地面均设为无滑移壁面。列车气动荷载作用位置见图5。

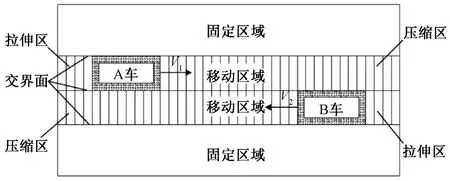
图4 网格分区示意

图5 列车气动荷载作用示意(单位：m)

2.2 计算结果

基于气动模型分别计算10、20、30 m/s风速下列车以100、200、300 km/h运行时列车和桥梁的气动荷载。工况用“风速(m/s)-车速(km/h)”形式表示，如10-100表示风速为10 m/s、车速为100 km/h工况。

列车交会时，两车之间的高速气流受到强烈挤压，同时迎风侧列车(A车)对背风侧列车(B车)产生遮挡作用，列车周围的流场显著改变，列车的气动荷载将产生明显变化。图6给出20-300工况下A、B两车头车气动荷载的计算结果，由于图中正负号仅代表力(或力矩)的方向，此处定性分析是基于气动荷载绝对值大小进行的。由图6可知，A、B两车气动荷载大小在未交会段较为接近，但在交会过程中受瞬态压力波的影响，两车气动荷载在交会开始与交会结束时发生明显突变。图6(a)和图6(c)表明，A车阻力和升力在交会开始时突然增大交会结束时突然减小，B车阻力和升力反而在交会开始时突然减小交会结束时突然增大。图6(b)和图6(d)表明A车侧力和侧滚力矩在交会开始时突然减小交会结束时突然增大，而B车侧力和侧滚力矩在交会开始时突然增大交会结束时突然减小，与A车变化规律相反。图6(e)和图6(f)表明，两车点头力矩与摇头力矩在交会时的突变情况更为复杂，交会开始时与交会结束时均分别出现两次突变。图7、图8列出了不同工况下迎风侧头车和桥梁跨中节段的气动荷载。

图6 20-300工况头车气动荷载

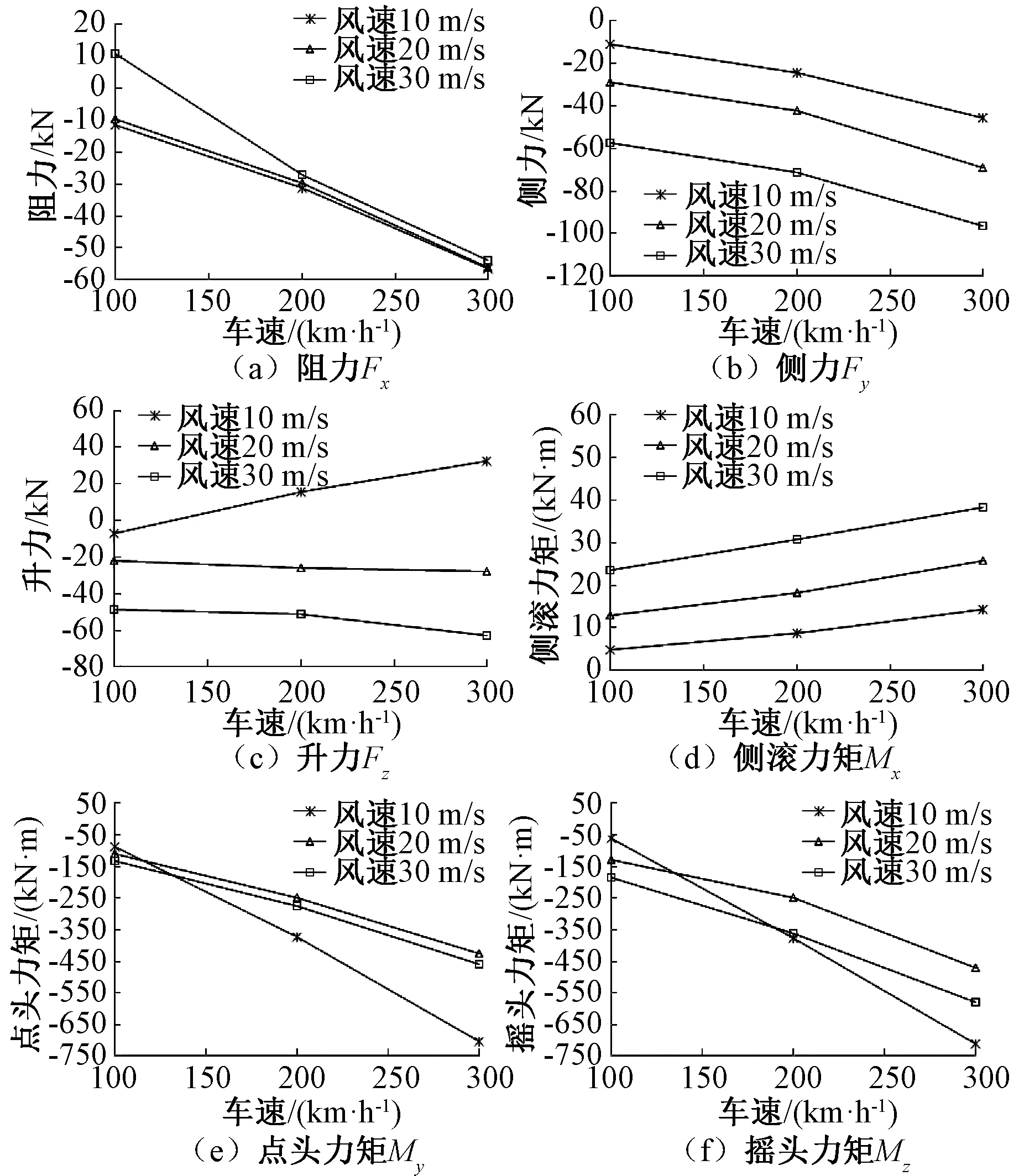
图7 迎风侧头车最大气动荷载

图8 桥梁跨中节段气动荷载

3 横风环境中列车-桥梁系统的动力学模型

3.1 列车动力学模型

列车动力学模型采用图9(a)所示的8节编组方式。动车模型共有17个刚体，拖车模型共有15个刚体，各刚体通过减振器、一、二系弹簧和抗侧滚扭杆等构件进行连接。车辆模型采用多体动力学软件Simpack建立[22-24]。模型中动车包含车体(1×6DOF)、转向架(2×6DOF)、轮对(4×6DOF)、电机装配(2×6DOF)和转臂定位(8×6DOF)，总计62个自由度，如图9(b)所示。拖车模型无电机装配，总计50个自由度。

图9 列车动力学模型

列车模型的轮轨接触几何关系如图10所示，本文模型采用S1002型车轮踏面以及UIC60型钢轨。轮轨相互作用力主要包括轮轨间的法向力和蠕滑力，轮轨法向力通过Hertz非线性弹性接触进行计算，蠕滑力则通Kalker简化理论Fastsim算法计算。

图10 轮轨接触几何关系

3.2 桥梁动力学模型

桥梁模型利用有限元软件Ansys进行建立，建模时通过空间杆系单元进行离散。模型共有8 702个节点和12 518个单元，其中主梁、桥墩和桥塔均采用梁单元(Beam44)进行模拟，斜拉索采用杆单元(Link10)进行模拟，并且采用节点耦合连接主梁与桥墩和桥塔。此外，利用均布质量对桥面的二期恒载进行模拟，桥梁的前10阶振型及频率如表1所示。

表1 自振频率及振型

4 横风环境中列车-桥梁系统耦合振动分析

4.1 联合仿真

首先选取合适的主节点并对桥梁有限元模型进行子结构分析，通过Simpack的前处理程序调用桥梁子结构分析的结果文件并生成FBI文件，从而将桥梁作为弹性体耦合集成到多体系统中。在多体系统中，轨道和桥梁之间通过约束连接，气动荷载通过时间激励施加到桥梁和列车上。Simpack控制积分过程，列车和桥梁在轮轨接触面离散信息点上进行数据交换，从而实现列车和桥梁的耦合振动仿真模拟。其中，列车和桥梁的变形协调条件和力平衡条件为：

变形协调条件

ur(t)=ub(t,s)

(8)

力平衡条件

(9)

式中：ur(t)为轨道的位移；ub(t,s)为桥梁在顺桥向s处的位移；Y(t)、Q(t)分别为轮轨的横向力和垂向力；Fy(t)、Fz(t)分别为轨道和桥梁之间约束的横向力和垂向力。

横风作用下列车-桥梁系统的仿真流程如图11所示。基于联合仿真方法，采用德国低干扰轨道谱作为轨道激励，对风速10、20、30 m/s与车速100、200、300 km/h的组合工况进行仿真计算。

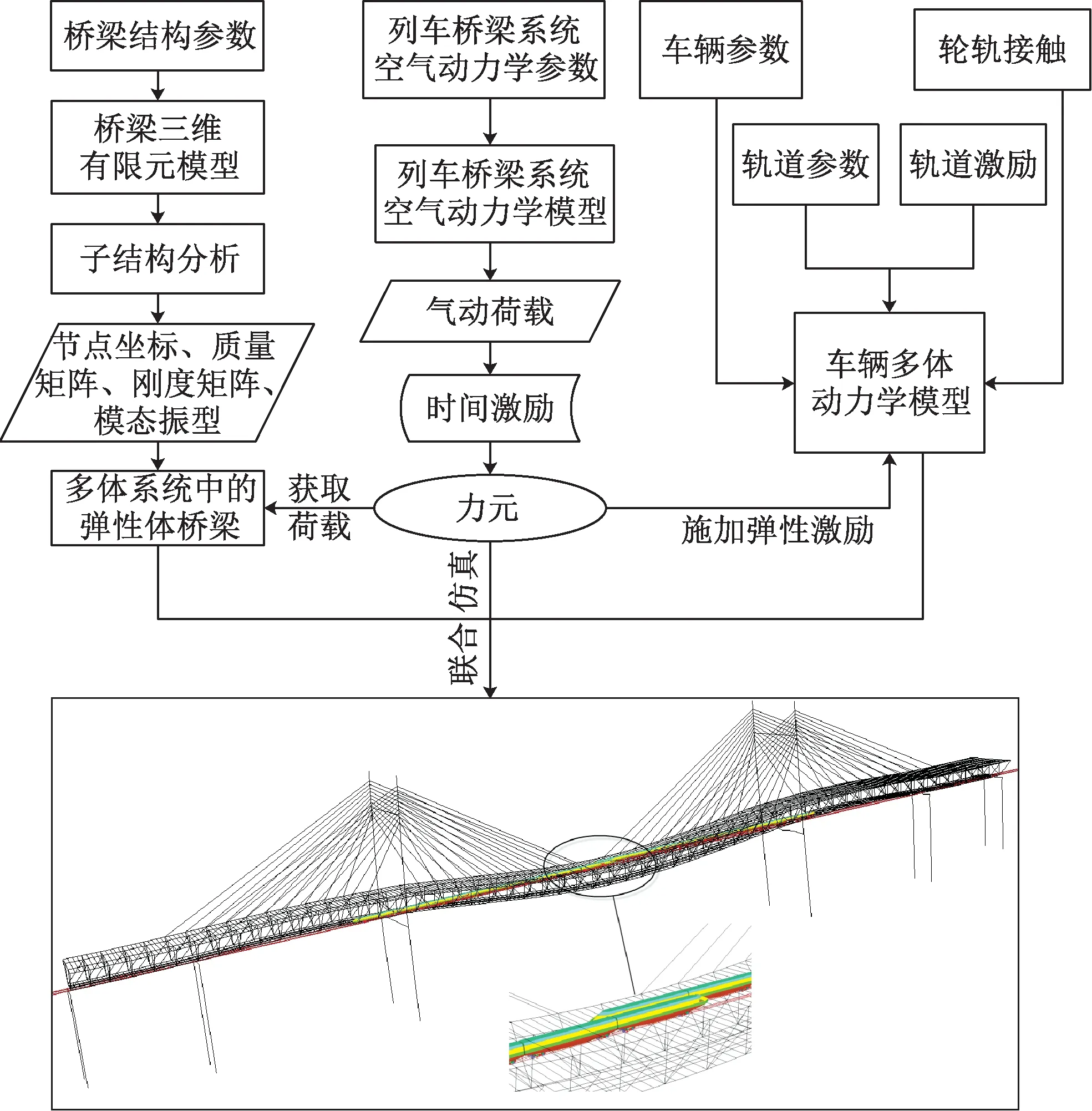
图11 仿真流程图

4.2 桥梁的动力响应

列车通过桥梁时，各工况主跨跨中的最大位移和最大加速度如图12所示。

图12 桥梁主跨跨中动力响应

由图12可知，横风环境双线会车时，随着风速的增大，主跨跨中竖向位移变化很小，对应车速下最大增幅仅3.64%，主要是因为列车自重荷载在主跨跨中竖向位移中起绝对的主导作用；主跨跨中横向位移随风速的增大显著增大，风速影响的最大增幅高达4.56倍；主跨跨中竖向和横向振动加速度随风速的增大亦明显增大,对应车速下竖向加速度最大增幅为32.8%，横向加速度最大增幅为23.9%。

在所研究的风速和车速工况下，主跨跨中竖向挠跨比、横向挠跨比、竖向振动加速度及横向振动加速度各动力学指标均满足文献[25-27]的规定。

4.3 列车的动力响应

表2给出了各工况迎风侧列车的脱轨系数、轮对横向力、轮重减载率、车体加速度及舒适度指标。计算结果表明，同一工况下头车的动力响应在列车的各节车辆中均为最大，表3列出了背风侧头车的动力响应。

由表2和表3可知，双线行车时，随着风速和车速的增大，车辆的安全性指标(脱轨系数、轮对横向力及轮重减载率)和舒适性指标(车体加速度及舒适度指标)均呈增大趋势。

当风速不大于30 m/s且车速不超过300 km/h时，列车的脱轨系数和轮对横向力均能满足要求，但轮重减载率、车体加速度和舒适度指标不能完全满足要求[25-27]。图13和图14给出了30-300工况迎风侧头车的轮重减载率和横向加速度。由图可知，列车行至桥梁跨中时轮重减载率出现最大值，车体横向加速度在两车交会时发生突变出现最大值。

为获得不同风速列车安全运行的临界车速，且考虑到各工况背风侧的轮重减载率均低于迎风侧，图15给出迎风侧头车轮重减载率与车速的关系曲线。同样，为得到舒适运行的临界车速，图16给出各风速下迎风侧头车的横向车体加速度与车速的关系曲线。

由图15可知，双线会车时为保证行车的安全性，当风速为10 m/s时，车速限值为296 km/h；当风速为20 m/s时，车速限值为256 km/h；当风速为30 m/s时，车速限值为147 km/h。

表2 迎风侧头车动力响应

表3 背风侧头车动力响应

图13 轮重减载率时程曲线

图14 车体横向加速度时程曲线

图15 轮重减载率与车速关系曲线

图16 迎风侧头车横向加速度与车速关系曲线

由图16可知，双线会车时为保证乘客的舒适性，当风速为10 m/s时，车速限值为166 km/h；当风速为20 m/s时，车速限值为150 km/h；当风速为30 m/s时，车速限值为106 km/h。

5 结论

基于计算流体力学、多体动力学及有限元技术构建仿真平台，针对平潭海峡大小练岛水道公铁两用斜拉桥，高速列车选用CRH3型，结合Fluent、Ansys和Simpack软件对横风环境中列车-桥梁系统的空气动力学模型和多体动力学模型进行仿真分析，主要得到以下结论：

(1)横风环境双线会车时，随着风速的增大，主跨跨中竖向位移变化很小，而主跨跨中横向位移随风速的增大显著增大，主跨跨中竖向和横向振动加速度随风速的增大亦明显增大。在所研究风速和车速工况下，桥梁的挠度和振动加速度均能满足要求。

(2)横风环境中列车在桥梁上运行时，各节车辆的动力学指标存在差别，其中头车的动力特性最为不利，可通过头车的动力指标评定整车的安全性与舒适性。随风速和车速的增大，车辆的各动力学指标均呈增大趋势。列车行至桥梁跨中时轮重减载率出现最大值，两车交会时车体横向加速度发生突变出现最大值，车体轮重减载率、车体加速度和舒适度指标不能完全满足要求。

(3)双线会车时，风速在10、20、30 m/s的临界安全车速分别为296、256、147 km/h，临界舒适车速分别为166、150、106 km/h。